补贴策略在网络零售平台竞争中真的有效吗？——基于寡头竞争模型的理论与实证研究

徐振宇，陈昱州，向洪金

(1.南京审计大学 统计与数据科学学院，江苏 南京 211815；2.江苏省政府统计与大数据研究院，江苏 南京 211815；3.南京审计大学 经济学院，江苏 南京 211815)

一、引 言

近年来，中国网络零售规模持续快速增长。从2011年开始，中国网络零售额就跃居全球第二位。(1)麦肯锡：《中国网络零售革命：线上购物助推经济增长》，https://www.cisco.com/web/CN/partners/industry/pdf/retail_industry_03.pdf，2013年3月。根据商务部的数据，2013年中国已成为全球最大的网络零售市场。此后，中国网上零售市场延续了高速增长态势，2014年至2019年的增幅分别高达49.7%、33.3%、26.2%、32.2%、23.9%和16.5%。2020年受新冠肺炎疫情影响，在社会消费品零售总额同比下降3.9%的情况下，网上零售额增速仍达10.9%。(2)根据国家统计局官方网站数据计算得出。商务部发布的《中国电子商务报告2020》显示，2020年中国网上零售额达11.8万亿元，其中实物商品网上零售额9.76万亿元(占社会消费品零售总额的比重达24.9%)。

伴随网络零售规模持续快速增长，网络零售平台化发展趋势日益明显——阿里巴巴(3)作为中国网络零售平台的先行者之一，阿里巴巴在平台竞争中不断改变其战略和组织架构。2011年，为适应新形势，尤其是更好地与快速成长的京东商城展开竞争，阿里巴巴旗下的淘宝网一分为三，其中，淘宝网负责C2C业务，一淘网负责搜索业务，淘宝商城(天猫)负责B2C业务(后更名“天猫”)。初创即为网络零售平台(以下简称零售平台)，曾作为垂直电商的京东、苏宁易购也日益发展成零售平台，拼多多、快手、抖音是近年来涌现出的新型社交零售平台。以拼多多为代表的社交零售平台，借助社交裂变、用户拉新，直接联合重点品牌商，凭借“团购”“砍一刀”等新方式，重点在手机数码、美妆、母婴等多个品类进行持续补贴(所谓“百亿补贴”)，在加快中国网络零售平台化进程的同时，也导致中国网络零售平台间更加激烈的竞争。

围绕网络零售基本经营方向的选择，即究竟是致力于做自营还是做平台抑或是选择混合模式，国内外学界进行了大量的研究。Smith和Hay(2005)通过建立购物中心间的竞争模型，比较了三种零售组织模式的竞争结果[1]。骆品亮和傅联英(2014)分析了传统商超模型、会员费、佣金制和两部收费制等模式下零售企业的转型路径[2]。Hagiu和Wright(2015a)分析了网络零售首选平台模式的三种情形[3]，又研究了双边平台商业模式与三种传统替代方案转换的影响因素(2015b)[4]。Tian等(2018)发现，当订单履行成本高且供应商产品相似时，纯自营模式是首选；当订单执行成本较小，产品差异较大时，纯平台模式是首选；当订单执行成本适中且供应商的产品相似时，首选混合模式[5]。

在平台经济背景下，明显的网络外部性与马太效应以及相关的高额固定成本，导致零售平台间的竞争日趋激烈。部分平台为获得未来的垄断地位，愿意也有能力(往往通过多层次的资本市场进行多轮融资)承担长期亏损。正如我们所看到的，亚马逊、淘宝、拼多多等著名平台型企业曾多年亏损，甚至有企业从来没有盈利却市值高得惊人[6]。零售平台之间的竞争手段也不断更新，其中，名目繁多的补贴是一种非常重要的竞争手段(亏损的重要来源，就是针对平台的供应商和用户持续发放的巨额补贴)。

补贴策略对市场结构、行为、绩效以及政府政策都会产生不容忽视的影响。本文感兴趣的基本问题是，补贴策略在网络平台竞争中是否真的有效？围绕上述问题，国内外已有文献主要围绕两方面展开研究。

一是平台竞争中的定价问题。Rysman(2009)研究了网络平台调节费用与设定准入机制的策略[7]。Rochet和Tirole(2006)建立了包括平台使用率和消费者网络效应的双向市场模型，推导并解释了最优定价公式[8]。段文奇和柯玲芬(2019)建立了一个在不同用户规模下的两阶段定价模型，发现提高用户规模可以显著提高平台利润[9]。二是与定价高度相关的问题，即零售平台补贴策略有效性问题。补贴策略在网络零售和诸多服务平台竞争中均广泛存在，但是，对于补贴策略在网络平台竞争中的有效性，学界尚未有文献展开深入研究。胡东波等(2016)建立仿真模型讨论了在市场中已存在一个垄断平台的情境下，新进入的平台如何通过补贴策略抢占市场[10]。Li和Huang(2019)基于双边市场理论建立双边用户的效用函数，研究了药品电商零售平台常用的补贴策略及其效果[11]。Cai等(2021)发现补贴策略在赢得物流服务平台市场竞争中起着重要作用[12]。

总体而言，国内外已有文献多着眼于零售平台经营方向的选择(如以自营为主还是以平台为主，抑或是混合模式)，并未深入探讨零售平台间的战略互动尤其是基于补贴策略的战略互动，也未区分补贴策略在短期与长期中的不同效应。从零售平台的现实竞争情境看，研究基于零售平台寡头竞争的补贴策略互动，区分补贴策略在短期与长期中的不同效应，对于更好地理解零售平台竞争，完善零售平台治理，有着重要的理论意义和实践价值。

本文将重点研究零售平台竞争中补贴策略在短期和长期中的选择：通过建立古诺寡头模型推导出补贴力度对平台消费者数量和市场份额的短期影响；分析长期中零售平台最优补贴率的动态变化；最后通过中国主要零售平台上市财报数据进行经验分析。本文的边际贡献在于，将时间因素考虑进零售平台竞争模型中，构建短期和长期中不同的目标函数，区分补贴策略在短期与长期中的不同效应；在静态寡占博弈竞争基础上，进一步通过动态平台补贴策略模型进行更深入的研究，对理解网络零售平台补贴策略的基本逻辑，优化网络零售平台治理，均有重要的借鉴价值。

二、为“活下去”而补贴：零售平台竞争的静态模型

理论上，在初始阶段，零售平台可以采取三种基本策略：一是通过先吸引更多的供应商(店铺)入驻平台，然后间接吸引消费者加入并使用平台；二是通过先吸引更多的消费者加入平台，然后吸引更多的供应商(店铺)入驻平台；三是同时吸引更多的供应商(店铺)和更多的消费者加入平台。在消费者规模较小的初期，消费者对平台上产品数量的交叉网络效应系数较大[13]。消费者根据各平台上的供应商(店铺)、供应商提供的商品及性价比等多种因素综合考虑是否在零售平台购物，而供应商则根据零售平台制定的入场费和佣金提成来决定是否入驻该平台售货，且供应商的定价与零售平台的上述费用政策有关。

根据梅特卡夫定律(Metcalfe’s Law)(Shapiro和Varian,1999)[14]，网络价值与联网用户数的平方成正比。在现实中，为了在具有显著双边市场效应的激烈竞争中“活下去”，多数零售平台在初始期往往会采取不同类型的免费政策(甚至倒贴)。而所谓的免费，并不是指平台对所有参与方都免费，也不是指长期免费。对于零售平台而言，消费者(用户)数量的增长至关重要。为实现财务上的可持续性，零售平台对消费者(用户)免费(甚至倒贴)的同时往往会对供应商收费。供应商在支付费用的前提下才能使其商品和服务被平台展示和推荐。实际上，国内外主要网络零售平台都采取对消费者免费而对供应商收费的策略，如表1所示，天猫商城、京东商城和亚马逊(美国站)均采用“固定年度/月度使用费+交易扣费”的两部收费制(Two-part Tariff)；拼多多、淘宝等平台目前没有固定的年度/月度使用费，也不收取销售提点，以免费入驻为特色吸引供应商加入(可视为固定年度使用费和交易扣费均为零)。

在现实运营情境中，零售平台往往对供应商收费，而对消费者免费。因而，可假设平台定价pA、pB与各自平台制定的入场费FA，FB(≥0)和佣金RA，RB(≥0)正相关(式中a为常数)：

pA=a+α1FA+α2RA,(α1,α2>0)

(1)

pB=a+α1FB+α2RB,(α1,α2>0)

(2)

表1 主要零售平台典型商品的供应商费率结构(单位：元)

假设各平台的供应商数量(nA，nB)与该平台的入场费和佣金负相关，与其竞争的平台的入场费和佣金正相关，也就是说当A零售平台收取费用越少，B零售平台收取费用越多时，那么A零售平台就越可能吸引更多的供应商加入(式中b为常数)：

nA=b-β1FA+β2FB-β3RA+β4RB,(β1,β2,β3,β4>0)

(3)

nB=b-β1FB+β2FA-β3RB+β4RA,(β1,β2,β3,β4>0)

(4)

假设选择A平台的消费者数量mA与A平台供应商数量nA正相关，与B平台供应商数量nB负相关。因为一个零售平台的供应商数量越多，相应地，商品种类一般也会越多，就更容易吸引更多消费者使用，而更多的消费者使用又会吸引更多的供应商加入，这种典型的网络外部性还会对消费者和供应商产生“锁定效应”，从而对产品定价、供求协调和市场结构都产生极为复杂的影响。

为解决“先有鸡还是先有蛋”的问题，先假设供应商在初始阶段不考虑各平台的消费者数量，但消费者会考虑根据零售平台上供应商数量来选择零售平台。设θ为补贴率，假定消费者偏好更低价格的零售平台，因此，A平台的消费者数量与该平台补贴后价格(1-θA)pA负相关，与竞争平台B平台补贴后价格(1-θB)pB正相关。γ1,γ2分别代表消费者对两个零售平台供应商数量的网络外部性，γ3,γ4分别代表消费者对两个零售平台价格的敏感程度。有时网络外部性会影响消费者的价格敏感性，反映到式子中有可能表现为γ1>γ3，γ2>γ4，也就是网络外部性大于消费者的价格敏感性(式中c为常数)：

mA=c+γ1nA-γ2nB-γ3(1-θA)pA+γ4(1-θB)pB,(γ1,γ2,γ3,γ4>0)

(5)

mB=c+γ1nB-γ2nA-γ3(1-θB)pB+γ4(1-θA)pA,(γ1,γ2,γ3,γ4>0)

(6)

为简化分析，借鉴经典的古诺模型，假设两个平台地位平等，因此只需单独研究其中一个平台，下文将只研究A平台。

在零售平台竞争的初始阶段，各零售平台会更注重消费者的数量，以消费者数量最大化为决策出发点。故将消费者数量mA对补贴率θA求导：

(7)

结论1：消费者数量mA与零售平台的补贴率θA正相关。

因而，对于零售平台而言，为获得更多消费者数量而采取补贴策略是有效的。

相关的推论有二：

推论1-1：零售平台收取入场费FA和佣金率RA越高，增加补贴水平会吸引更多的消费者。

换而言之，平台在对供应商采用两部收费制的同时，对供应商收取的入场费和交易佣金越高，对消费者采取更高的补贴水平，将会带来更高的消费者数量增长率。

推论1-2：消费者价格敏感度γ3越大，增加补贴率对消费者数量增加的促进作用就越大。

也就是说，当市场中对价格敏感程度较高的消费者人数越多时，平台采取补贴策略对“抢夺”消费者数量的效果就越好；反之，如果市场中大多数消费者对价格不敏感，平台采取补贴策略对“抢夺”消费者数量效果就越差。

将消费者数量mA分别对入场费FA和佣金RA求导：

(8)

(9)

结论2：网络外部性(γ1,γ2)和消费者对价格的敏感程度γ3越大，更高的入场费FA和佣金率RA对消费者数量mA的负效应就越大。

也就是说，网络外部性越明显，同时消费者对价格越敏感，更高的入场费FA和佣金率RA将会导致消费者数量的减少。相应地，就有如下的推论：

推论2-1：零售平台即使只对供应商收费，费用最终还是会由消费者和供应商共同承担。

实际上，供应商如果被收取较高的入场费和佣金，会倾向于提高产品的价格。考虑网络外部性与价格敏感程度的双重影响，将会提高消费者成本并降低该平台消费者的数量。从而有如下进一步的推论。

推论2-2：对供应商的高收费往往会间接影响加入该平台消费者的数量mA。

而采取更高的补贴率，则可以适当减少平台对供应商较高的收费导致的消费者流失情况。因此，大致又可以得出一个推论：

推论2-3：为吸引消费者加入，降低对供应商收取的入场费和佣金与提高对消费者的补贴率，可视为两种互替的策略选择。

为更全面地对短期内零售平台的补贴策略进行分析，还应考虑对消费者的补贴力度与市场份额(为简化分析，下文用消费者数量作为市场规模的代理变量)的关系。加总上文的式(5)和式(6)，可得市场总的消费者数量为：

m=mA+mB=2c+(nA+nB)(γ1-γ2)+(γ3-γ4)[pA(-1+θA)+pB(-1+θB)]

(10)

A平台的市场份额(A平台消费者数量/总消费者数量)为：

(11)

为研究A平台市场份额与A,B两平台各采取补贴率大小的关系，把市场份额SA对补贴率θA，θB求一阶导，得：

(12)

(13)

结论3：某平台的市场份额与该平台的补贴率正相关，与竞争平台的补贴率负相关。

上述三个结论，从不同角度表明，为了在具有显著双边市场效应的市场的激烈竞争中“活下去”，通过增加补贴力度，网络零售平台可以获得更多的消费者(用户)和更高的市场份额；且消费者价格敏感度越大，补贴率的增加对消费者(用户)数量增长的促进作用越大。

三、“可持续运营”：基于最优补贴率的零售平台动态决策模型

考虑寡头垄断的动态竞争模型过于复杂，本文借鉴讨论垄断企业的古典埃文斯(Evans)模型[15]，聚焦研究在市场中只存在单一平台企业垄断时的补贴策略选择，研究在平台垄断情形下平台补贴水平随时间变化的动态趋势。

假设参与平台的供应商数量n和价格p只取决于时间t，这里我们延续静态分析时的假设，平台的供应商数量和价格不由网络外部性决定，而是只与平台原始禀赋有关，这里加入时间因素为了分析长期的动态平台竞争变化(式中a，h为常数)，由此：

n=a+b×t,(a,b>0)

(14)

p=h+i×t,(h,i>0)

(15)

假设参与平台的消费者数量m不仅与时间t有关，也取决于补贴率θ(t)和补贴率的变化率θ′(t)，这里的消费者数量随着时间因素变动，会被较高的补贴率而吸引，而且会对补贴率的变动作出反应，补贴率θ(t)是关于时间t的函数(式中d为常数)，由此：

m=d+e×t+f×θ(t)+g×θ′(t),(d,e,f,g>0)

(16)

平台的利润为：

π=R×p×n×m+F×n-θ(t)×p×n×m

=(a+bt){F+R(h+it)[d+et+fθ(t)+gθ′(t)]-(h+it)θ(t)[d+et+fθ(t)+gθ′(t)]}

(17)

式(17)是一个关于时间t、θ(t)和θ′(t)的动态利润函数。平台的目标是找到补贴率θ(t)的一个最优路径使得在有限时期[0，T]上的总利润∏[θ(t)]达到最大。我们假定补贴率θ(0)=0，并且显然补贴率θ(t)是在0到1之间。

(18)

s.t.θ(0)=0

0≤θ(t)≤1

πθ′θ′=0

(19)

πθθ′=-g(a+bt)(h+it)

(20)

πθ=-(a+bt)(h+it)[d-fR+et+2fθ(t)+gθ′(t)]

(21)

πtθ′=bg(h+it)[R-θ(t)]+(a+bt){giR-eht-eit2-d(h+it)+

fR(h+it)-[gi+2f(h+it)]θ(t)-2g(h+it)θ′(t)}

(22)

得到欧拉方程：

πθ′θ′+πθθ′+πtθ′-πθ=g{R(bh+ai+2bit)-[bh(1+t)+bit(2+t)+

a(h+i+it)]θ(t)-(a+bt)(h+it)θ′(t)}=0

(23)

解该微分方程得到上述问题的解，最优补贴率路径为：

(24)

从式(24)不难看出，在使得长期中动态利润最大化的最优补贴率路径方程中，没有入场费F，也就是说，作为一次性买断收入的入场费F对零售平台的长期利润最大化没有影响，这与我们在第二部分平台竞争静态模型中得到最优补贴率与入场费大小无关的结论相一致。

结论4：入场费对使得零售平台长期利润最大化的最优补贴率路径没有影响。

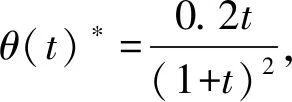
图1 最优补贴率动态变化

结论5：在长期中，零售平台最优补贴力度随时间变化而变化，补贴率与时间呈倒U形关系，即开始阶段逐步提高补贴力度，超过某个时段后将逐渐平缓降低补贴力度。

最大值为0.05，在t→1时取得，最优补贴率θ(t)*与时间t的关系呈倒U形，在开始时刻t=0时，零售平台应该不断提高补贴率，当t超过某一特定时刻时，零售平台应该降低补贴力度来维持利润最大化。

从图1可以直观看出，在零售平台刚进入市场时，补贴率增长得较快(曲线比较陡峭)；超过一定时点后开始降低补贴率，此时补贴率减少得较慢(曲线较为平坦)。上述数值模拟结果与零售平台的现实竞争情境基本相符：鉴于平台经济显著的双边市场特征，为了在激烈的市场竞争中“活下去”，零售平台在刚进入市场时不得不持续增加补贴力度以吸引更多消费者(用户)并扩大市场份额，从而往往表现为亏损的扩大；但是，上述积极的补贴策略将在长期中使零售平台陷入财务困境，当经过某个时点后，为实现财务上的可持续性，零售平台将不得不逐步降低补贴力度，同时利用累积起来的市场份额，以增加融资、降低运营费用、拓展业务领域、增加广告收入、提升交易效率，促进平台使用方及平台自身的合作共赢，推进可持续商业模式的设计与创新，以减少亏损，最终实现利润水平的增长。另外，随着政策和监管体制的完善，零售平台的投资和补贴力度将会趋于合理，并寻求利润[16]。

当然，上述结论的关键假设是在市场中单一的平台企业已经获得事实上的垄断地位，不存在新平台进入的实质性威胁。如果存在新的平台企业进入的实质性威胁，上述数值模拟的结论就需要作出相应的调整。一旦有新的平台准备进入，或已经进入，现有平台的最优补贴策略显然不是降低补贴力度，而有可能是推出比新平台更大的补贴力度。上述更复杂的情形，只能是另一篇论文的研究主题。

四、基于中国主要零售平台的经验分析

(一)数据来源及说明

为了对上文的数理推导结果与数值模拟结果进行经验检验，有必要采用现实生活中的数据进行必要的计量经济学分析。下文用于经验分析的所有数据，均来源于中国三个主要的零售平台阿里巴巴、京东和拼多多的季度财务报告。考虑数据的可获得性，本文使用的是上述三家零售平台2018年第一季度到2021年第二季度共14个季度的财报数据。

下文将各平台季度财报中的截至年底的活跃用户数简称为活跃用户数，将用于销售和营销的费用支出视为近似的补贴费用(拼多多公告宣传的“百亿补贴”数据其实也是出自该数据)。关于营销收入这项数据，各零售平台财报中的具体“名称”各异：对于阿里巴巴，本文选用“核心商业：中国零售商业—客户管理”(在阿里巴巴财报中的相关注释为“为更好地反映对商家的价值创造，把佣金收入作为客户管理收入的一部分列报”)；对于京东，本文选用的是市场和广告收入；对于拼多多，本文选用的是网络营销服务及收入。为直观呈现补贴费用增加与营销收入、活跃用户数的影响，绘制各零售平台上述三项数据随时间变化趋势图如图2、图3和图4所示。

图2 阿里巴巴的营销收入、补贴费用和活跃用户数

图3 京东的营销收入、补贴费用和活跃用户数

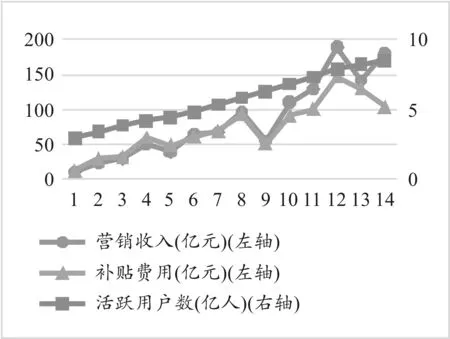
图4 拼多多的营销收入、补贴费用和活跃用户数

将上述三张图结合起来看，不难发现，中国主要零售平台的营销收入、活跃用户数均随补贴费用的增长而增加。下文将量化分析补贴对网络零售平台收入和用户数的影响，将检验两个基本问题：一是营销收入与补贴是否正相关？二是用户数量与补贴水平是否正相关？

(二)计量模型及结果

1.营销收入与补贴是否正相关？鉴于数据的可得性，采用如下的固定效应模型：

lnRit=αi+β1lnSit+β2lnBit+β3lnBit×lnSit+β4lnEit+it

(25)

其中，被解释变量为营销收入(Marketplace Revenues)增长率，即为营销收入的对数。解释变量lnSit为补贴增长率，lnBit为活跃用户增长率，lnBit×lnSit为两者的交互项，选取的控制变量lnEit为研发费用增长率。t为时间变量，t=1,2,…,14(从2018年第一季度到2021年第二季度，每个季度为一个时段)。

表2 补贴增长率对营销收入增长率影响的回归结果

表2表明，营销收入增长率随着当期补贴增长率的提高而提高，且结果在5%水平下显著；营销收入增长率随着活跃用户数增长率的提高而提高，结果在5%水平下显著。二者对营销收入系数均为正，对营销收入增长有着显著促进作用，与第二部分数理模型的解释一致。

补贴增长率和活跃用户数增长率的交互项的系数为负且在5%水平下显著，这表明补贴增长和活跃用户数增长对营销收入增长的促进作用是互相替代、互相排斥的，也就是在动态利润函数那里推导出倒U形最优补贴率曲线一致，在开始时增加补贴力度会吸引用户加入促进利润增长，超过一定值时也就是在有一定用户基础以后要降低补贴力度。因此，本文得出在有很高的用户基础上降低补贴力度对促进营销收入增长会有帮助的结论。

2.用户数量是否与补贴水平正相关？鉴于数据的可得性，设计如下固定效应模型：

lnBit=αi+β1lnSit+β2Eit+it

(26)

表3 补贴增长率对活跃用户数增长率影响的回归结果

其中，被解释变量为活跃用户数增长率，即为活跃用户数的对数。解释变量lnSit为补贴增长率，选取的控制变量Eit为研发费用。

表3表明，活跃用户数增长率随着当期补贴增长率提高而增加，结果在1%水平下显著，这与第二部分数理模型得出的结论一致。控制变量研发费用系数为负，在1%水平下显著，表明增加研发成本本身对用户增长存在负向影响，可能是因为研发对补贴费用有挤出效应。

3.稳健性检验。为检验补贴增长率对企业收入增长率影响的回归结果的稳健性，控制股票市场的影响，增加可以反映股票市场活跃度的季度平均成交量作为控制变量，设计如下固定效应模型：

lnRit=αi+β1lnSit+β2lnBit+β3lnBit×lnSit+β4lnEit+β5lnVit+εit

(27)

表4 补贴增长率对营业收入增长率影响的回归结果

被解释变量为营销收入(Marketplace Revenuse)增长率。解释变量lnSit为补贴增长率，lnBit为活跃用户增长率，lnSit×lnBit为两者的交互项，选取的控制变量lnEit为研发费用长率及反映股票市场的季度平均成交量lnVit。

表4表明，在增加控制变量后，营销收入增长率随着当期补贴增长率提高而增加，结果在5%水平下显著；营销收入增长率随着活跃用户数增长率提高而提高，结果在5%水平下显著，系数均为正；两者交互项系数为负且在5%水平下显著，大体上与基准结果一致，只是显著性水平略有不同。股票季度平均成交量增长率系数为正且在5%水平下显著，表明股票长期成交量增加对促进营销收入有正向影响。

(三)进一步的讨论

图2、图3和图4中的数据还显示，三大零售平台的季度补贴费用大致呈波动式上升，主要原因在于，各大零售平台会在特殊时间节点(例如“618”及“双11”)显著增加促销与补贴力度，因而，补贴费用会随着季度和平台策略的季度差异而波动，但上升趋势基本一致。事实上，近年来三大零售平台都主动或被动地转向“百亿补贴”的“补贴战”，其中特别值得注意的是拼多多。从图4不难看出，作为一个新进入网络零售市场的平台，拼多多近年来一直维持着高补贴状态，2021年第一季度用于销售与市场推广费用为129.974亿元，同比增长高达78%，营销收入和活跃用户数也随补贴额度的持续增长而快速增长。在很大程度上受拼多多持续巨额补贴的冲击，在中国网络零售市场排名第一和第二的阿里巴巴和京东，也都显著增加了补贴力度。出现上述类似“特征化事实”的情形，可能的原因大致有二：第一，可能是因为近年来各平台间的竞争尚处在上文预测的动态最优补贴率拐点的左侧，此时补贴水平还有可能继续上升，直到一定时点后补贴水平才可能出现下降；第二，也可能是因为各平台间的竞争在某种程度上陷入了“囚徒困境”，以拼多多为代表的后进入者不得不通过提高补贴率增加用户数量，而以阿里巴巴和京东为代表的“在位者”面对新进入者的巨额补贴也不得不增加补贴，从而形成平台间日益激烈的补贴竞争。

五、结论与展望

本文区分了短期和长期，在短期构建了一个静态的古诺寡头博弈模型，研究零售平台的寡占竞争策略中的补贴策略，回答了零售平台如何通过采取补贴策略来获取用户基础和市场份额；在长期和动态分析中，求解出最优补贴率的变动趋势(一个随时间变动的倒U形趋势)。数理模型分析研究发现，在短期，零售平台采取补贴策略对消费者增长和市场份额有着明显正向促进作用，从而有利于在激烈的竞争中“活下去”(此时根本不会考虑利润，而且“成功”的零售平台在相当长的“短期”内一般都是亏损的)。在长期时，求解欧拉方程得到动态最优化补贴率后，发现最优补贴率会随时间呈倒U形：在进入市场时倾向于增加补贴率，超过一定时段后通过降低补贴率以实现利润最大化，从而确保可持续运营。计量经济学分析发现，补贴费用增长对营销收入和消费者(用户)数量的增长率具有显著的正向促进作用，基本证实了前文数理模型所指出的补贴策略在零售平台寡占竞争中的重要作用。

本文的研究也存在一定的局限性。为理论分析之便利，在理论模型构建中，假设供应商仅通过零售平台的收费水平选择零售平台，虽然存在消费者数量对供应商数量的网络外部性假设，但不存在供应商数量对消费者数量的网络外部性策略性互动，这是一项较强的假设。另外，在动态分析中，考虑到寡头垄断的动态竞争模型过于复杂，本文只分析了市场中仅存在单一垄断平台的补贴率的动态变化。实际上，分析零售平台间的动态竞争远比上述分析复杂，这也将是我们后续研究的重点。