基于模糊神经网络的桥基防渗方案最优比选分析
2022-05-11宋紫朝
宋紫朝
(北京市政路桥管理养护集团有限公司,北京 100000)
1 研究背景
随着国内经济的快速发展,目前对城市交通的要求也在逐渐提高,城市交通的便利程度直接影响着城市经济发展及居民生活的便利性[1-2]。随着现如今国家对环境的要求,对城市水系的要求也是逐渐提高,因此,为连接城市交通,对城市桥梁的质量要求也随之提高[3-4]。地基对桥梁工程质量的影响十分关键,良好的地基质量直接影响桥梁工程的使用寿命,由于桥梁工程基础位于水下,因此采用合理的防渗措施对桥基进行维护至关重要,将直接影响桥梁工程的质量及稳定性[5-7],因此对于城市桥梁工程来说,合理的桥基防渗措施十分关键。
目前,对于工程地基防渗的研究已取得了一定的进展。郝磊[8]以渠道地基为研究对象,比较了混凝土等不同防渗措施的防渗效果,指出混凝土防渗措施在不同措施中对地基的防渗效果最优;曹丽娟等[9]研究了水库地基的最优防渗措施,由于研究对象位于岩溶地区,因此防渗措施的实施十分关键,她比较了垂直防渗帷幕、局部粘土水平铺盖和整体土工膜水平铺盖三种方案的防渗效果,指出局部粘土水平铺盖措施为防渗效果最优的措施;温立峰等[10]研究了混凝土防渗措施对坝基的防渗效果,指出该措施是透水和可压缩坝基渗流控制的主要措施。
桥梁地基若出现渗水,对整个桥梁工程的质量将产生十分严重的影响,为找出适用于桥基防渗的最优措施,本文选择原土夯实、浆砌石和混凝土三种防渗措施,通过监测入渗速率初步分析不同措施的土壤防渗效果,同时基于模糊神经网络模型,对不同措施不同方面进行综合评价,以期得出适用于桥基防渗的最优措施。
2 桥基防渗效果评价指标体系构建
为从多方面综合比较三种方案的效果,选出最优方案,本文从方案的实施合理性、方案的经济性和对环境的影响性三个方面,共12 个评价指标建立桥基防渗方案综合评价指标体系,具体体系构建情况见表1。

表1 评价指标体系构建
3 评价方法基本步骤
3.1 模糊神经网络
Takagi 和Sugen 于1985 年构建了T-S 模糊神经网络模型,该模型基于IF-THEN 的原则,当假设规则为yi时,具体模糊评价步骤为:
将模糊数据集的相对隶属度进行模糊计算,最终得出计算结果的输出值。
3.2 灰色聚类-SPA 理论
本文基于灰色聚类-SPA 理论,对不同防渗措施的优劣性,而灰色聚类-SPA 理论的具体步骤如下:
对传统白化函数及三角白化权函数进行改进,构造指数型白化函数,改进后的函数曲线是平滑的,扩大了函数涵盖范围[9]。将防渗措施防渗效果划分为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ共五个区间。具体函数模型如下:
(1)当k=1,Ⅰ等级对应灰类指数型函数模型为:
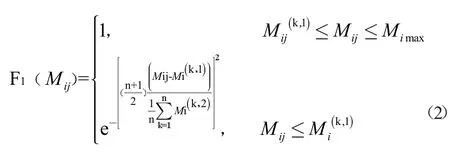
(2)当2≤k≤n-1,Ⅱ、Ⅲ、Ⅳ等级对应灰类指数型函数模型为:
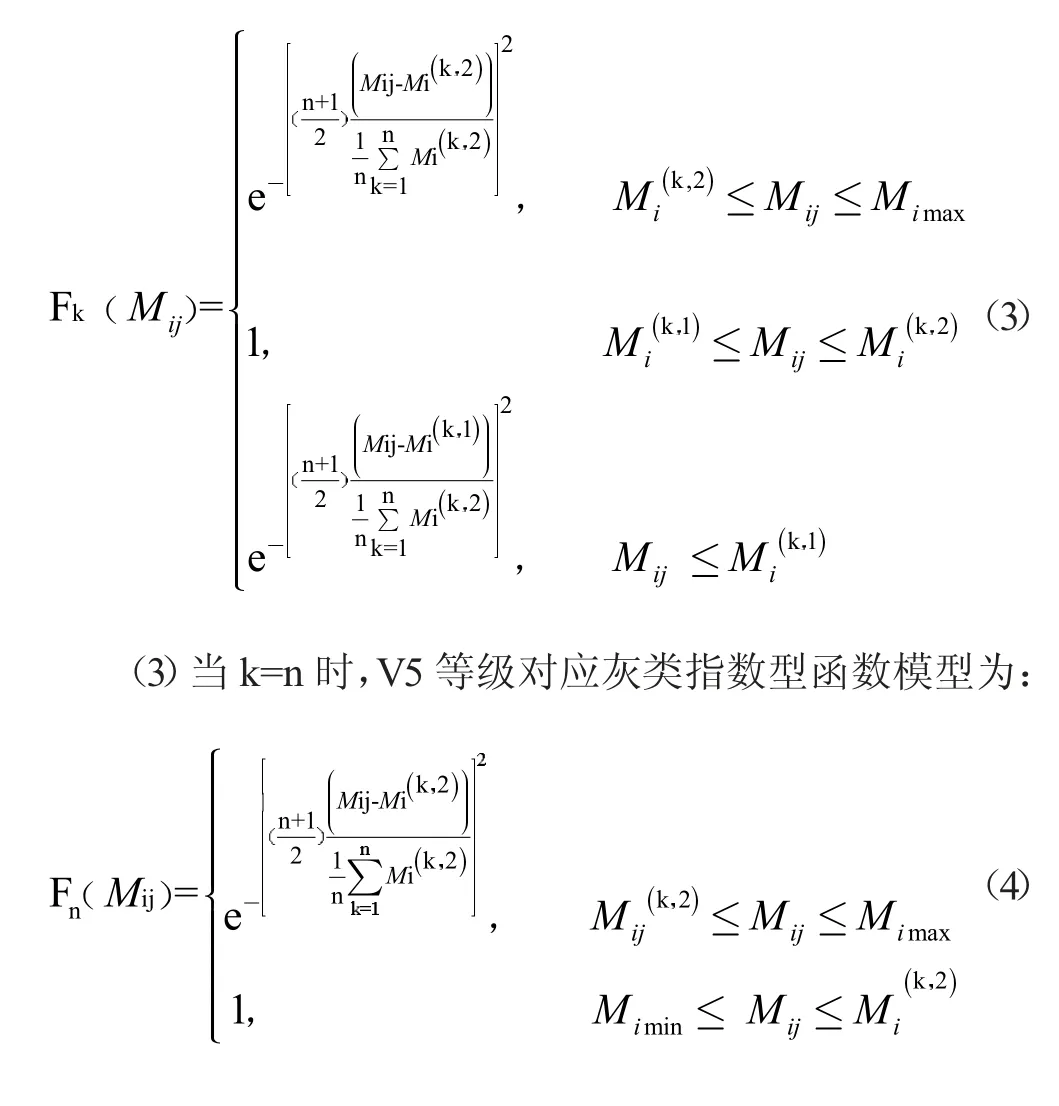

公式中ak、bk、ck、dk、ek称为联系度分量,分别反映指标k 对已划分的5 级灰类区间V1-V5 等级的偏向度;j为对立系数,通常取-1;m3、m2和m1为评价样本与评价等级的差异度系数。
将区间[-1,1]平均划分成(n-1)个子区间,各分点值从左到右分别与式(7)中j m3、m2和m1的值相对应,利用同样的均分原则将区间[-1,1]进行n 等分,从左到右可分别得到五个评价等级的区间范围。具体评判区间如下:
当0.6≤μk≤1.0 时,判定级别为好(Ⅴ);当0.2≤μk≤0.6 时,判定风险级别为较好(Ⅳ);当-0.2≤μk≤0.2时,判定风险级别为一般(Ⅲ);当-0.6≤μk≤-0.2 时,判定风险级别为较差(Ⅳ);当-1.0≤μk≤-0.6 时,判定风险级别为差(Ⅴ)。
结合集对分析SPA 理论与灰色聚类评价,运用上述函数模型,计算各评价指标相应的聚类系,与SPA 模型的联系度分量ak、bk、ck、dk、ek建立如下函数关系:

式中θi1、θi2、θi3、θi4、θi5分别为指标i 的五个聚类系数分量。
各指标i 在不同灰类下的聚类系数由改进的指数型白化函数式(1)-(6)计算得到,采用式(10)进行归一化处理:

4 不同措施效果比较
4.1 不同措施土壤入渗速率对比
图1 为不同防渗措施下的桥基土壤入渗速率对比。由图中可以看出,随着时间的增长,不同方案的土壤入渗速率变化趋势均为先降低后平稳的趋势,而土料夯实措施下的土壤入渗速率最高,在100min 内的平均入渗速率为0.38cm/s,而浆砌石措施和混凝土措施的土壤平均入渗速率相差不大,分别为0.22和0.21cm/s,土壤累积入渗量表现为相似的变化规律。不同措施的土壤入渗速率不同,在土料夯实措施下的土壤入渗速率仍然较快,而浆砌石和混凝土的入渗速率相近,混凝土入渗速率略优于浆砌石措施,但考虑到相同面积下,浆砌石的投资要低于混凝土,所以初步选择浆砌石防渗为桥基防渗的主要措施。
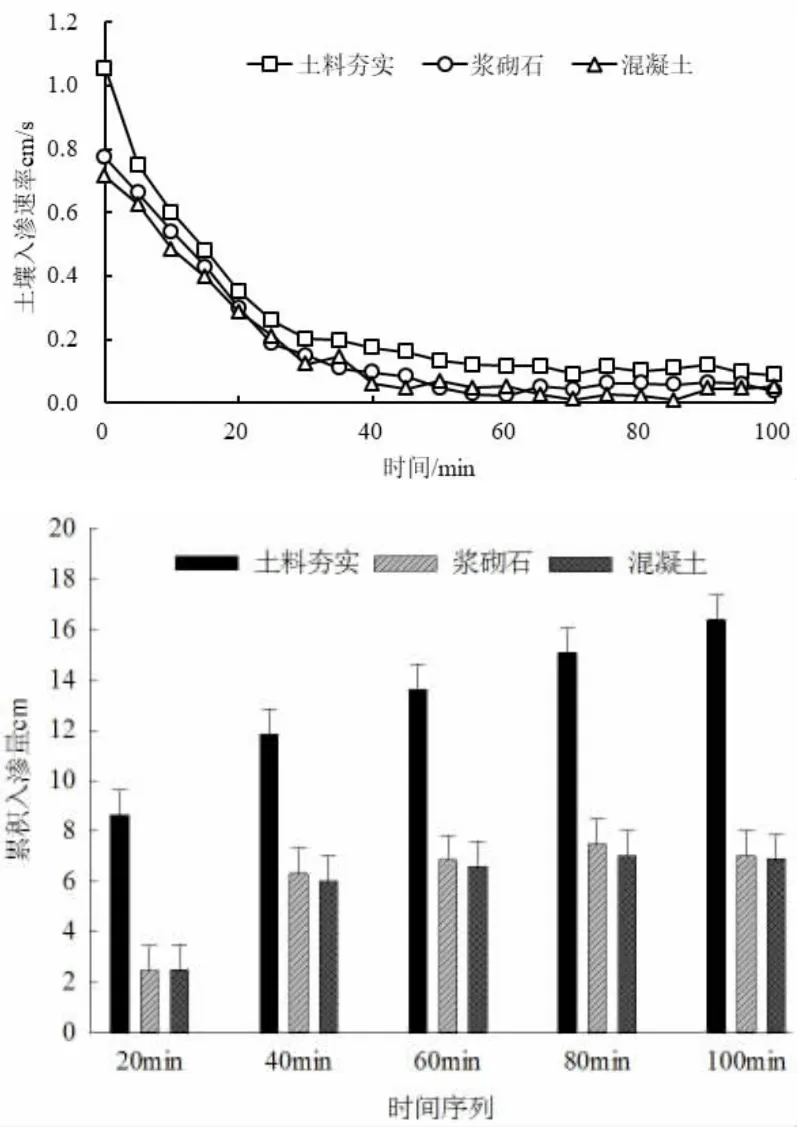
图1 不同防渗措施土壤入渗速率对比
4.2 不同方法最优防渗措施方案比选
首先根据AHP 法的基本原理,确定第二层准则层指标的权重,确定准则层指标判断矩阵,结果见表2。然后确定不同指标的相对隶属度矩阵,结果见表3。根据表3 和表4 中的数据,得出指标最终权重,结果见表5。

表2 准则层指标判断矩阵

表3 第三层指标相对隶属度矩阵

表4 第三层指标初始综合权重

表5 第三层指标最终综合权重
土料夯实措施各联合度分量计算数据,结果见表6。由表6 中的数据可以看出,土料夯实年算得的综合联系数为-0.194,达到了一般的标准,同理得出浆砌石综合联系数分别为0.207,虽然增幅较低,达到了较好的标准,同时,浆砌石方案虽然入渗速率略高于混凝土措施,但综合比较后发现,由于混凝土的造价较高,施工较复杂,浆砌石方案为桥基防渗的最优方案。
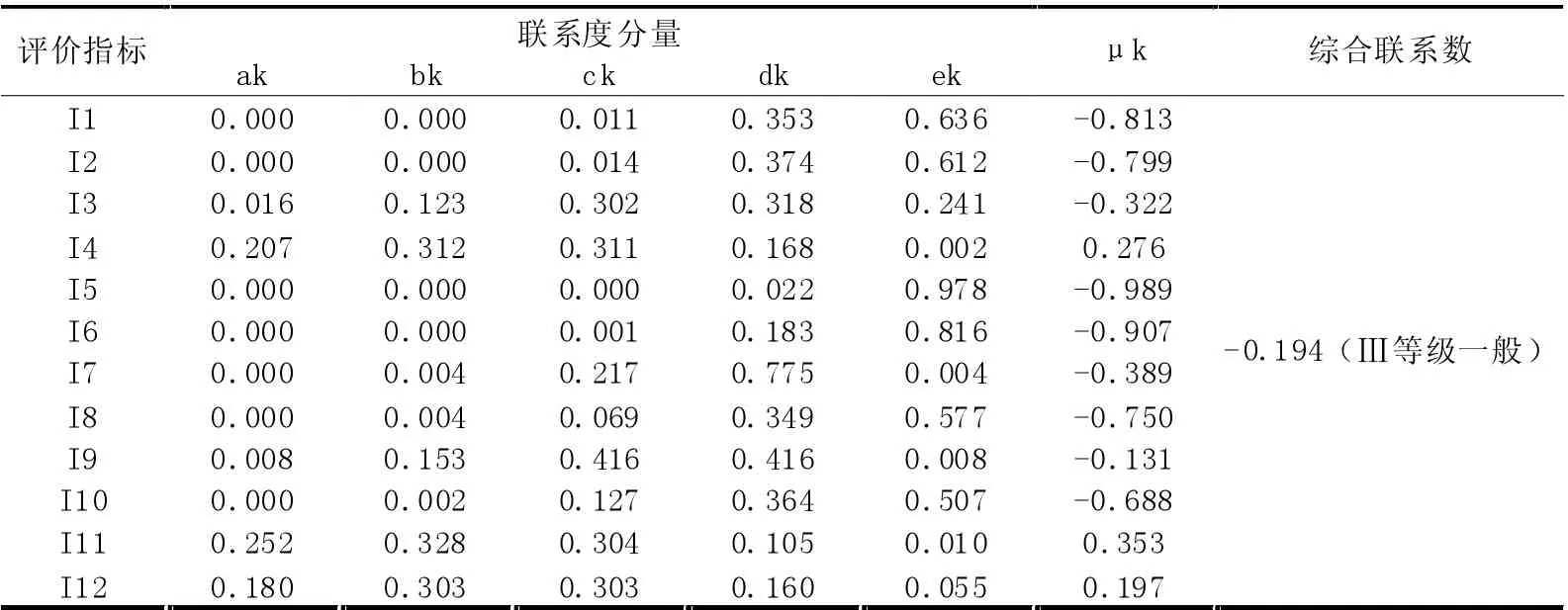
表6 土料夯实措施综合联系数确定
表7 列出了模糊神经网络对不同桥基防渗措施效果的评价标准,不同防渗措施的防渗效果可见表8,由表中可知,浆砌石措施和混凝土措施的防渗效果均达到了较好,且浆砌石措施较优。同时模糊神经网络的运算时间远低于SPA 理论,因此,证明了该方法的适用性。
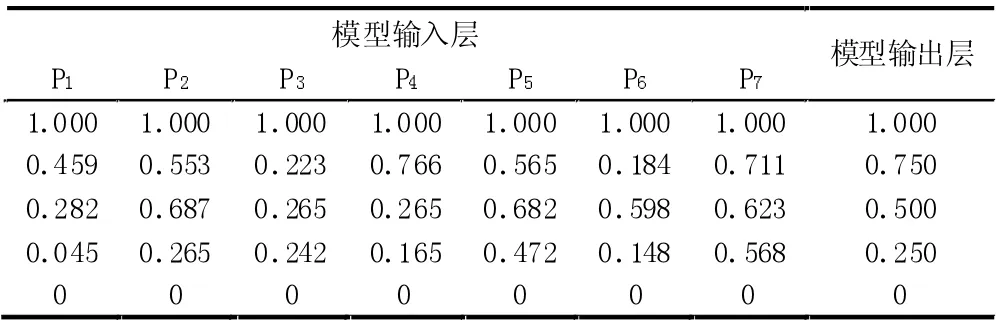
表7 模糊神经网络评价标准
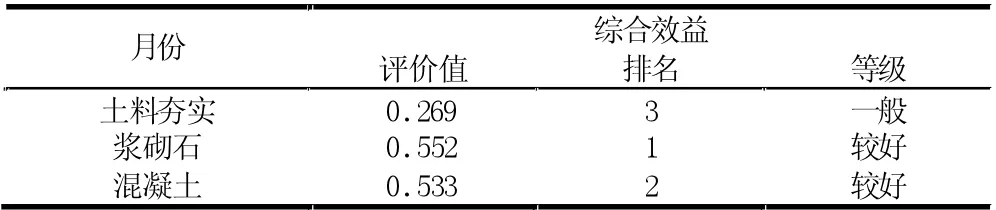
表8 模型输出结果
5 结论
本文基于模糊神经网络对不同桥基防渗方案效果进行了比较,从方案的实施合理性、方案的经济性和对环境的影响性三个方面构建了桥基防渗方案评价指标体系,同时将模糊神经网络模型计算结果与传统的SPA理论进行了对比,证明了该模型的适应性。
