Separation Characteristics and Structure Optimization of Double Ellipsoid Cone Double-Field Coupling Demulsifier
2022-05-11GONGHaifengQIUZhiPENGYeYUBaoLIAOZhixiangCHENLingYANGYang
GONG Haifeng, QIU Zhi, PENG Ye, YU Bao, LIAO Zhixiang, CHEN Ling, YANG Yang
(1.Engineering Research Centre for Water Oil Recovery Technology and Equipment of Ministry of Education, Chongqing Technology and Business University, Chongqing 400067, China; 2.Chongqing Key Laboratory of Manufacturing Equipment Mechanism Design and Control, Chongqing Technology and Business University, Chongqing 400067,China; 3.State Key Laboratory of Heavy Oil Processing, China University of Petroleum, Qingdao 266580, China)
Abstract: Demulsification and dewatering of oil-water emulsion is a key process in the fields of petrochemical industry and oilfield exploitation. The swirl device has a great influence on the internal flow field and separation efficiency. In this study, a new coupling device was proposed, of which the cone section was an ellipse tangent structure instead of the design mode of straight double-cone section. A model for numerical simulation of the device was established, and the influence of the elliptic tangent structure on the internal flow field and separation efficiency of the device was studied. Moreover, a calculation model of the elliptic tangential device with different structural parameters was also established, and the structure of the elliptic tangential swirl device was optimized by Box-Behnken factor design and response surface method. The results show that the separation efficiency of the elliptical tangent structure is higher by about 5.98% than that of the straight double-cone structure. After optimization, the optimal values of major axis a1, minor axis b1 of ellipse 1, and major axis a2 of ellipse 2 are 560, 90 and 409.96 mm, respectively, and the corresponding dewatering rate is about 96.23%.
Key words: structural optimization; separation characteristics; elliptic tangent type; response surface method; coupling device
Water in oil (W/O) emulsion is common in petrochemical industry, oilfield exploitation, resources, and environment. Demulsification and dewatering of emulsion is a key process[1-3]. At present, physical, chemical and biological methods can be used for the dewatering of emulsion[4-6]. The most common physical methods include electric field, gravity settling, swirl centrifugal and vacuum heating[7-9].
In general, efficient demulsification and dewatering of emulsion are difficult to be achieved by using a single emulsion dewatering method[10-13]. Thus, a combination or integration of various methods or unit operations is recommended for efficient demulsification and dewatering[14-17]. The combination of electric field and swirl centrifugal methods can achieve high efficiency for demulsification and dewatering of emulsion and satisfied separation effects. Electric field method intensifies the collision of droplets in emulsion, promotes the coalescence of droplets, and increases the particle size of droplets, however, it cannot achieve rapid and efficient separation[18]. Swirl centrifugal method is an effective and rapid separation method that is based on different densities of oil phase and water phase in emulsion. The water phase with higher density flows along the wall of the hydrocyclone device towards the underflow port, and the water phase with lower density flows from the shaft to the overflow port. At present, few studies have been reported on the coupling of electric field and swirl centrifugal field for demulsification and dewatering. For instance, Bailes et al.[19]has studied the demulsification and dewatering of emulsion under the condition of high-voltage pulsed electric field and proposed a continuous electrostatic demulsifier, which effectively coalesces and separates the emulsion under the combination of that two fields. Ni et al.[20]adopted a compound field dewatering device of high-frequency electric field and centrifugal field to promote the polymerization of the dispersed phase droplet of oilwater emulsion and improve the efficiency of oilwater separation of emulsion. Ghadiri et al.[21]investigated the demulsification and dewatering of emulsion by combining a pulsed DC electric field and a centrifugal field, and developed a centrifugal electric coalescence separator. The results showed that the device can make the droplets coalesce rapidly under the coupling action of the two fields and improve the separation efficiency. Adamski et al.[22]combined centrifugal force and electric field for treating emulsion by using the simultaneous action of centrifugal force and electric field to coalesce the emulsified water in the emulsion, and the device also uses a phase separator for effective separation to obtain improved separation effect.
Researchers have focused on the influence of the internal flow field characteristics and inlet structure on the separation characteristics of the swirling device under the coupling effects of the internal electric field and centrifugal field, while ignored the influence of the structure of the swirling device on the internal flow field and separation characteristics. For example, Wang et al.[23]studied the influence of hydrocyclone length and cone angle amplitude and diameter on hydrocyclone performance within a certain range of inlet flow rate. They found that increasing the length and diameter of hydrocyclone and reducing the cone angle amplitude are conducive to improving the separation efficiency. Li et al.[24]determined the influence of straight line and arc helix inlet structure on the separation characteristics, and the authors found that the helix inlet tube has the highest separation accuracy and the lowest cutting size. Han et al.[25]established a new concept which can be used to design a small swirl device at low inlet pressure, of which the separation efficiency can be increased by changing the length of the cone end.
This study analyzed the structure of an electric field cyclone centrifugal field coupling dehydration device. The double-field coupling dewatering device with double ellipses tangent section as cone section was proposed. A numerical calculation model of the coupling device was established to simulate and analyze the separation performance of the cone segment with different structures, and structural parameters of the cone segment with different double elliptic plane tangent types. The optimal cone segment structural parameters of the double elliptic plane tangent type device were obtained by combining Box-Behnken factor design and response surface method.
1 Model
1.1 Electric-centrifugal field coupling device
Fig.1 shows that structure diagram of the double-field coupling separation device. The traditional straight-face double-cone structure is shown in Fig.1(a). The structure presents gradient shape in the cone section, which causes internal vibration, promotes fluid instability, and affects separation efficiency. The double-ellipse tangent cone coupling separation device (Fig.1(b)) proposed in this study is mainly composed of centrosymmetric double tangential inlet, swirl chamber, overflow pipe, double-ellipse tangent cone, and underflow straight pipe. The positive electrode of the electric field is connected to the outer wall of the overflow pipe, and the external wall of the cyclone is grounded to apply high-voltage electricity to form a high-voltage electric field in the cyclone chamber. The emulsion droplet is stretched and deformed in the oil solution, which intensifies the collision of droplet, promotes the coalescence of droplet in the emulsion, increases the particle size of droplet, forms a smooth connection in the double-cone section, which avoids the vibration of the convection field caused by the gradient connection and achieves the efficient and rapid separation under the action of centrifugal field.
Double-ellipse tangent cone profile is constructed as follows: the interface between the large cone and the swirl chamber, with a point on the line intersecting the section of the coupling device as the center of
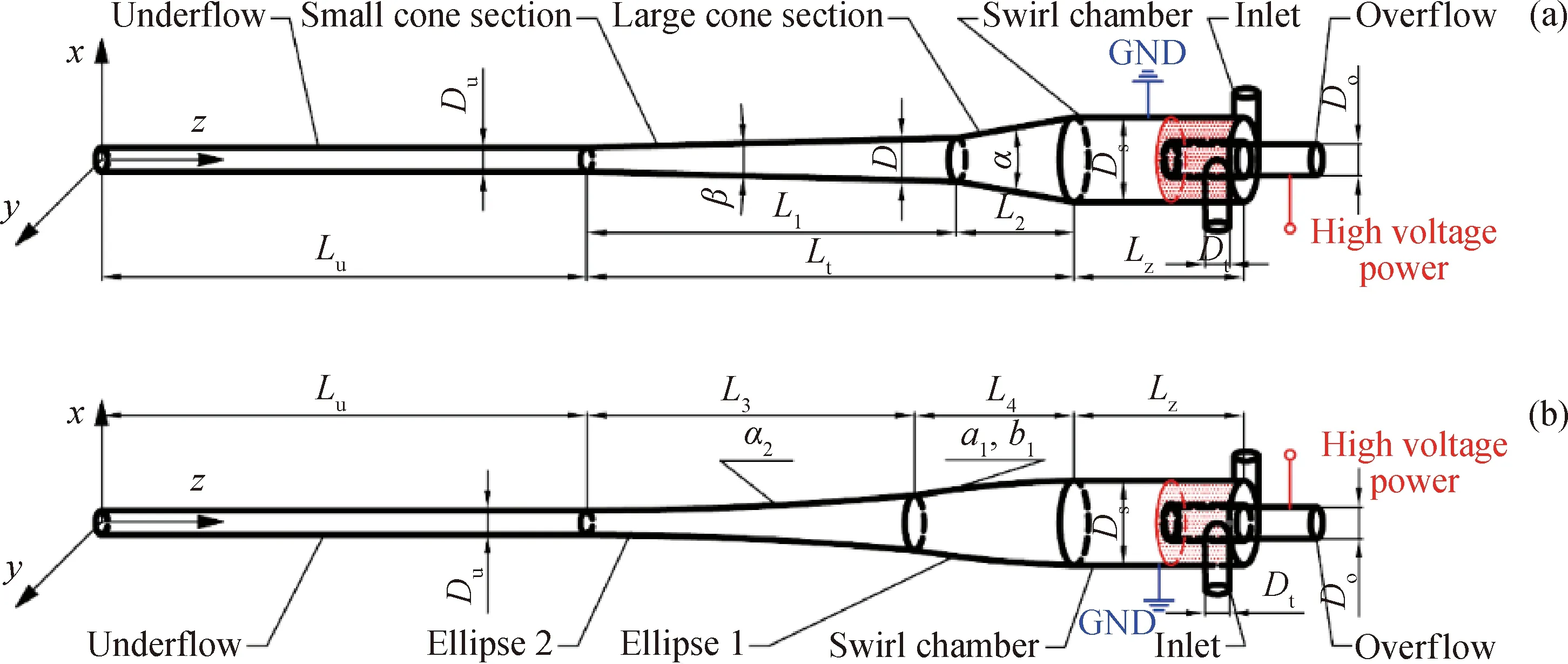
Du—The underflow port diameter, 10 mm; Lu—The underflow pipe length, 400 mm; Lt—The cone length, 430 mm;Ds—The cyclone chamber diameter, 70 mm; Lz—The cyclone chamber length, 75 mm; Do—The overflow port diameter, 18 mm;Dt—The entrance diameter, 12 mm; D—The nominal diameter, 30 mm; α—The big cone angle, 20°;β—The small cone angle, 3°;GND—Grounding.Fig.1 Structure diagram of the double-field coupling separation device(a) Structure diagram of straight double-cone coupling separation device;(b) Structure diagram of double-ellipse tangent cone coupling separation device
ellipse 1, the elliptic arc 1 is tangent to the cyclonic chamber of long axisa1and short axisb1, and the center of ellipse 2 is a point on the intersecting line between the interface of the small cone segment and the bottom flow tube and the section of the coupling device. The elliptic arc 2 with long axisa2is tangent to the elliptic arc 1 and the underflow pipe.
The profile curve of the coupling device is shown below:
Underflow pipe profile curve:
(1)
Conical section profile curve:
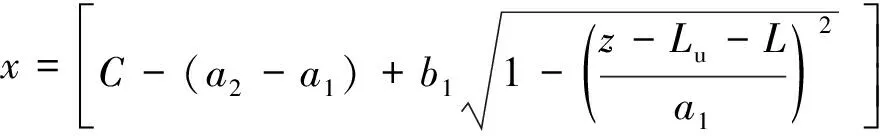
(2)
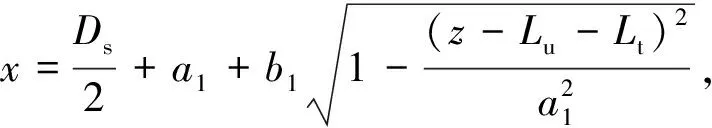
(3)
Cyclone chamber profile curve:
(4)
1.2 Governing equations
The studied demulsification and purification of emulsion in our work are a common multiphase flow separation process. The motion of continuous phase and dispersed phase is simulated by using the mixture model. The reason is that the mixture model is a simplified form of the Euler-Euler method. In the process of solving, only the momentum conservation equation of emulsion is solved, which has the characteristics of high efficiency, high accuracy and more stable calculation. This model can be used to simulate the situation of the wide distribution area of the dispersed phase in multiphase flow, the obvious difference of particle size, and the complex law of interphase drag force[26].
1.2.1 The continuity and momentum conservation equations
For incompressible fluid, the continuity and momentum conservation equations of oilwater two-phase flow mixing model are given as follows:
(5)
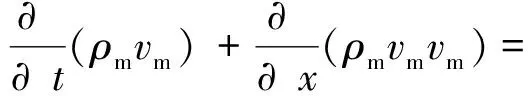
(6)
wherepis the pressure, Pa;Fis the external force, N;ρoandρware the densities of oil and water, respectively, kg/m3;αoandαware the volume fractions of oil phase and water phase, %;vdr,oandvdr,ware the drift velocities of oil phase and water phase, respectively, m/s;ρmis the density of oil-water mixture, kg/m3;vmis the velocity of oil-water mixture, m/s;μmis the viscosity of oil-water mixture, mPa·s; andidenotes the oil or water.
1.2.2 Volume fraction equation of oil phase[27]:
(7)
Wherevdris the relative velocity of droplet.
The flow characteristics of oilwater mixture, such as density, velocity and viscosity, are expressed as follows:
(8)
(9)
(10)
1.2.3 Electric field equation
The dispersed phase droplets will be affected by the electric field force in the electric rotary dual field coupling device due to the high-voltage electric field in the swirl chamber[28]. The electric field force is expressed as:
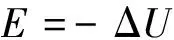
(11)
(12)
(13)
(14)
WhereUis the potential, V;Umis the voltage amplitude, V;tis the flow time, s;Tis the fluctuation period of the pulsed electric field;εois the vacuum dielectric constant;εris the relative dielectric constant.Ei(i=1,2,3) represents the electric field intensity along thex,yandzaxes, kV/m; andEj(j=1,2,3) represents the electric field intensity along thex,yandzaxes, kV/m.δis the kronecker symbol, andEis the effective amplitude of electric field, kV/m.
1.2.4 Coalescence equation
Under the action of electric fields, emulsion droplets collide and smaller droplets coalesce. According to the droplet coalescence model[29], the governing equation of droplet size are given as follows:
r′=2n/3r
(15)
n=[t/ts]
(16)
(17)
Wherer′ is the droplet size after coalescence, mm;ris the droplet size before coalescence, mm;nis the integral oft/ts;μis the dynamic viscosity of oil, Pa·s;αwis the volume fraction of water in the emulsion, %, andtsis the coalescence time of droplet in pairs, s.
The expression of droplet polymerization probability is given as follows:
(18)
WhereWe=ρ1Li{[1.43(εrLi)1/3]2+[1.43(εrLi)1/3]2}/σ;x=Li/Lj;c1is a constant of order unity;ρ1andρ2are the densities of the primary and secondary phases, kg/m3, respectively;LiandLjare the two colliding droplet diameters, mm;σis the conductivity of the emulsion, s/m.
1.2.5 Fragmentation equation
Based on the Hagesaether method[30], the crushing formula of discrete method is given as follows:
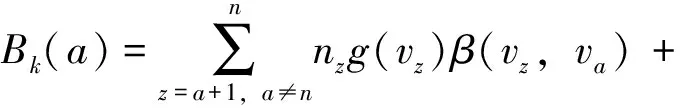
(19)
Wherenzis the volumetric number concentration of droplets with volumeVz;g(vz) is the integral droplet volume fraction at underflow, %;β(vz+1,vz) is the droplet distribution function;xa+1,zis the integral median of the interval (va+1,vz), mm.
1.3 Grid independence analysis
For the double-ellipse tangent cone model, three different mesh numbers (134685, 365786, and 643891) are divided in Fig.2. As shown in Fig.3, when the number of grids is 365786 and 643891, the structure of static pressure distribution and tangential velocity distribution is almost the same. Based on the time consumption and calculation results, the appropriate number of grids is 365786.
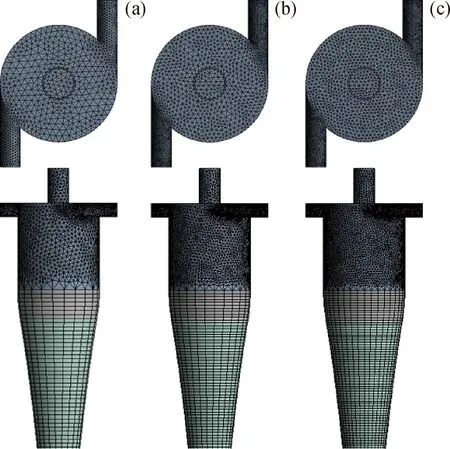
Fig.2 The computational grids generated by the model ofdouble-ellipse tangent cone segment(a) 134685; (b) 365786; (c) 643891
1.4 Boundary conditions
The boundary conditions of a new type of hydrocyclone with double-elliptic tangential cone structure are defined as follows: The turbulence intensity at the inlet of the cyclone separation device is set as 5%, and the hydraulic diameter is 12 mm. The normal velocity of the emulsion from the inlet
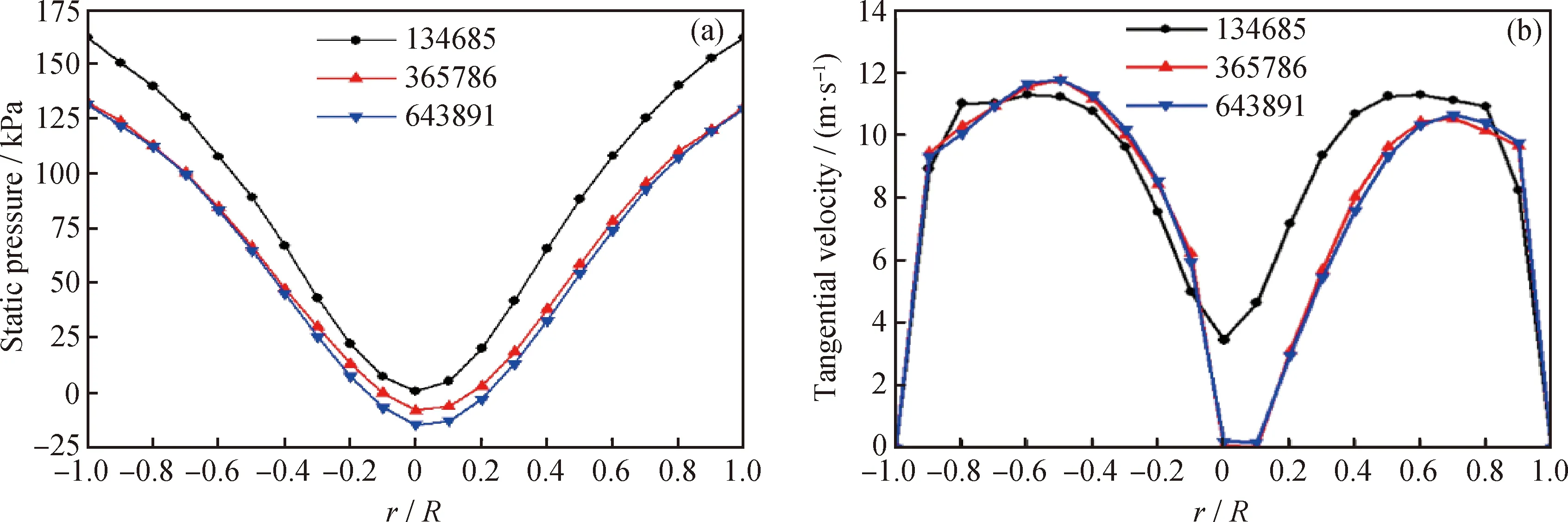
Fig.3 Static pressure distribution and radial tangential velocity distribution on the section z=700 mmunder three different mesh quantity conditions(a) Static pressure; (b) Tangential velocity
section of the cyclone separator is 10 m/s, the volume fraction of water in the emulsion is 10%, the overflow and underflow of the cyclone separator are outflow, and the inlet is velocity-inlet. The near wall surface is treated by the standard wall function, and the wall surface is treated by the nonslip boundary condition.
The physical parameters of oil and water are shown in Table 1.

Table 1 Physical parameters of oil and water
In this work, the numerical model was calculated at different cone structure parameters of coupling device by using software ANSYS Fluent (ANSYS 16.0). In the simulation, the Reynolds stress multiphase flow model was used. Linear pressure strain was selected in the Reynolds stress model, and the pressure solution method was used for simulation. The Semi-Implicit Pressure Linked Equations (SIMPLEC) algorithm was used to determine the coupling effects of pressure and velocity[31-32]. For turbulent motion, SIMPLEC improves convergence by using pressure velocity coupling as a constraint. In the spatial discretization region, the gradient was based on the least-squares element[31-32], and Pressure Staggered Option (PRESTO!) was used. QUICK was used for momentum, volume fraction, turbulent kinetic energy, and Reynolds pressure[31-32]. In the irregular structured grid, the least-squares unit has the characteristics of high precision and high efficiency[33]. The emulsion in the hydrocyclone separation device, under the PRESTO!, its flow pressure has a high discretization ability[33].
1.5 Structural parameter design
Assuming that the range of major axisa1, short axisb1of ellipse 1, and major axisa2of ellipse 2 are 540—560, 90—110, and 390—410 mm, respectively. Box-Behnken factor design and response surface methodology via Design-expert 8.0 software were used to optimize the size and levels of the double elliptical cones (Ellipse 1 major axis, minor axis, and ellipse 2 major axis, as shown in Fig.1(b)) of the new coupling device. The independent variables of the optimization design are major axisa1, short axisb1of ellipse 1, and major axisa2of ellipse 2 with double elliptical cone size. The dewatering rate of the overflow port of the new coupling device was taken as the response value. The level of each factor code was -1(a1=540 mm,b1=90 mm,a2=390 mm), 0(a1=550 mm,b1=100 mm,a2=400 mm), 1(a1=560 mm,b1=110 mm,a2=410 mm), respectively.
2 Experiment
In the experiment, the emulsion was prepared according to the oil and water volume ratio of 9∶1, and the continuous phase was No.46 engine oil. The physical parameters of the emulsion and water are shown in Table 1. Intermittent stirring was adopted in the configuration. After standing for 24 h, the droplet settlement separation was not obvious, which can meet the experimental requirements. The prepared emulsion was placed into the storage tank for standby.
Fig.4 shows the experimental device mainly including the single pump, pressure gauge, straight double-cone coupling device, high-voltage power supply, overflow tank, underflow tank, tee and valve. Tee ensures the same flow velocity at the two-way tangential inlet of the swirl device, as well as ensures tangential entry to reduce the energy loss. The volume of the overflow tank is 70 L, and that of the underflow tank is 25 L. During the operation of the device, the emulsion was injected from the inlet of the swirling device in a two-way axisymmetric manner, and the oilwater separation was carried out under the coupling effect of electric field and centrifugal field. As such, high-concentration oil flows out from the overflow port, and the droplets were discharged from the underflow port and entered the underflow tank. A small amount of
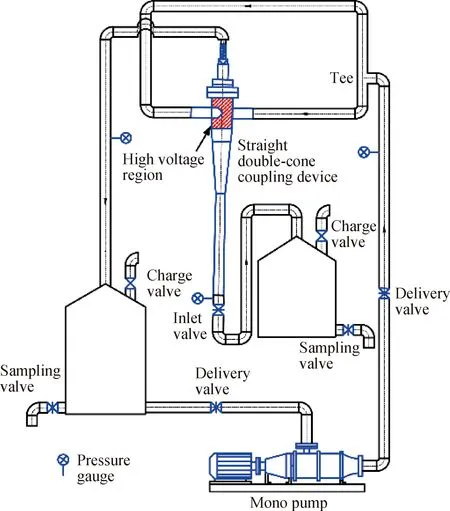
Fig.4 Schematic diagram of double-fieldcoupling experimental device
liquid was extracted by the sampling valve, and the water content or oil content in the sample was determined by a petroleum hygrometer (SYD-2212C). The dewatering rates are crucial parameters to measure separation performance of the double-field coupling device, and can be calculated according to the formula:
(20)
Here,Edwis the dewatering rate, %;fwois the water volume fraction discharged from overflow orifice, %;fwis water volume fraction of prepared emulsion, %. The change in pressure at all time should be monitored to avoid the influence of pressure on the separation efficiency and experimental safety.
3 Results and Discussion
3.1 Model verification
The rationality of the straight-face double-cone swirling device under different inlet flow rates was verified. Fig.5 shows the separation efficiency values obtained in the experiment (Average of five experiments) and numerical simulations. The experimental results of the straight double-cone swirling device are in good agreement with the numerical simulation results, although the former is slightly lower. In numerical simulations, the setting is basically an ideal environment with ignoring the change in emulsion temperature in the actual process and vibration deformation of the device. Therefore,
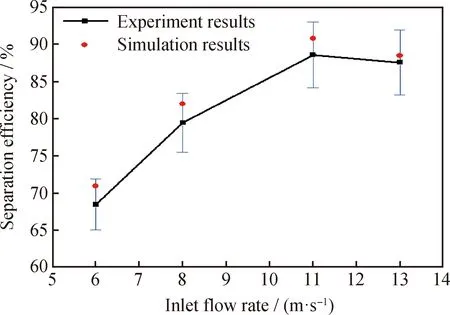
Fig.5 Experimental results and numerical analysis results ofstraight double-cone swirling device under differentinlet velocity conditions
the simulation calculation model of the straight-face double-cone swirl device is suitable for the internal flow field as well as for calculation and analysis of the separation efficiency of the electric field-centrifugal field coupling separation device.
3.2 Structure optimization of the new coupling device
3.2.1 Response model and variance analysis
Design expert 8.0 software is used to design the experimental independent variable level and factor code. The simulation calculations on different structures were conducted to obtain the response values under various test conditions. The results are shown in Table 2.
Design expert 8.0 software was also used in response surface analysis of the data summarized in Table 2, to establish ternary quadratic regression equation:
Edw=2068.68875-6.34525a1+0.40563b1-
1.40988a2-0.0053a1b1+0.00395a1a2+
0.001425b1a2+0.0049125a12+
0.0095875b12-0.0011125a22
(21)
Wherea1is the major axis of ellipse 1, mm;b1is the minor axis of ellipse 1, mm; anda2is the major axis of ellipse 2, mm.
According to variance analysis results of the ternary quadratic regression model (Table 3), theFvalue of the model is 9.85, and the corresponding p-value of the model is 0.32%. The response model is significant because Prob>Fvalue is less than 5%, thus, the response model of dewatering rate expressed in Equation (21) is significant. Moreover, the significant terms of the dewatering rate response model area1,a1b1, andb12.
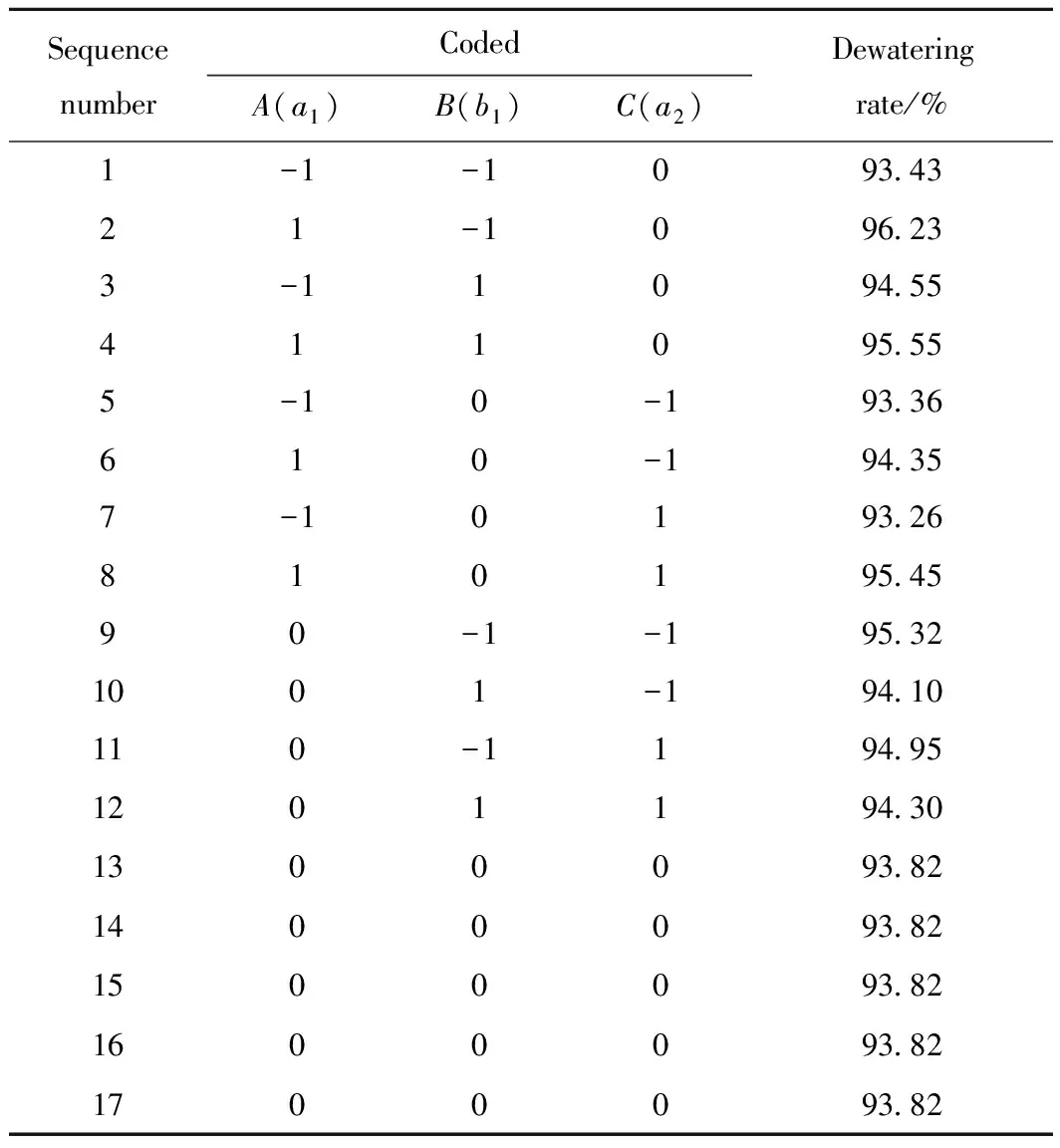
Table 2 Box-Behnken experimental design schemeand simulation results
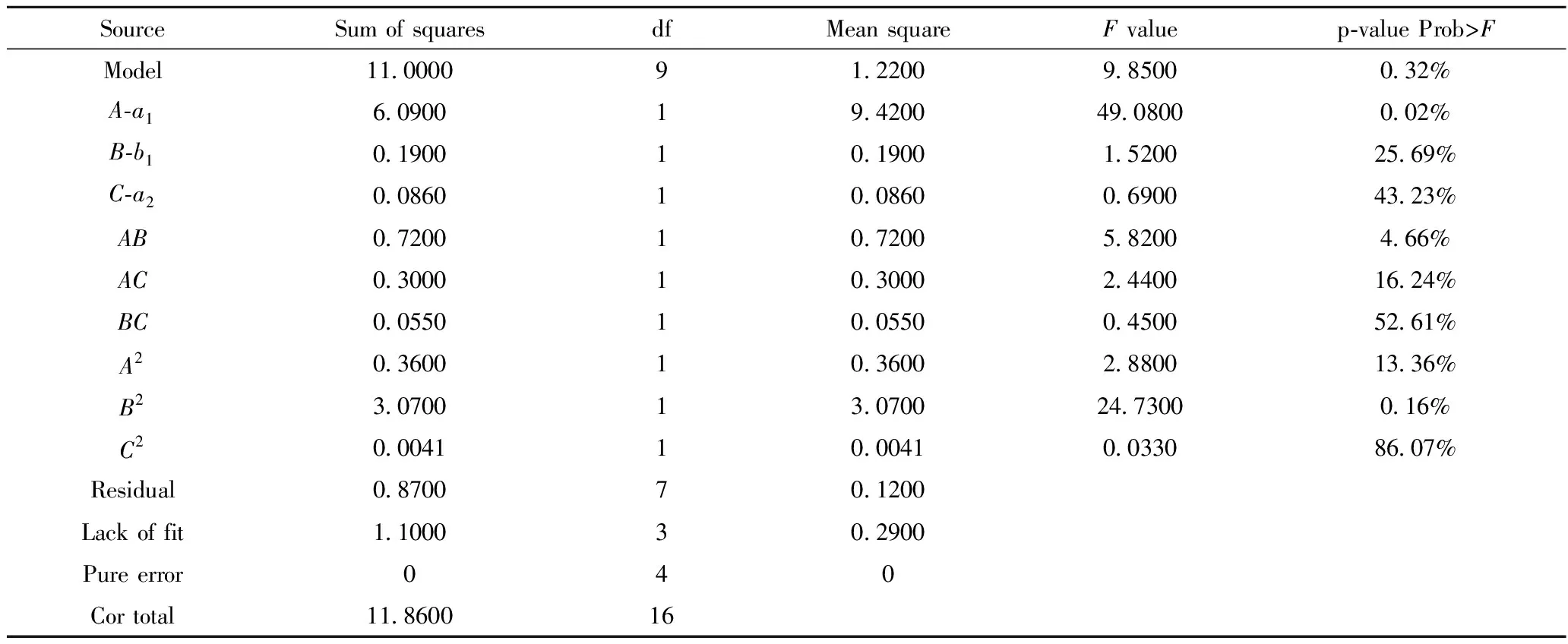
Table 3 Model ANOVA results of dewatering rate
Fig.6 shows that the numerical calculated value is relatively close to the predicted dewatering rate, indicating that the response surface model and the numerical calculation fit relatively well.
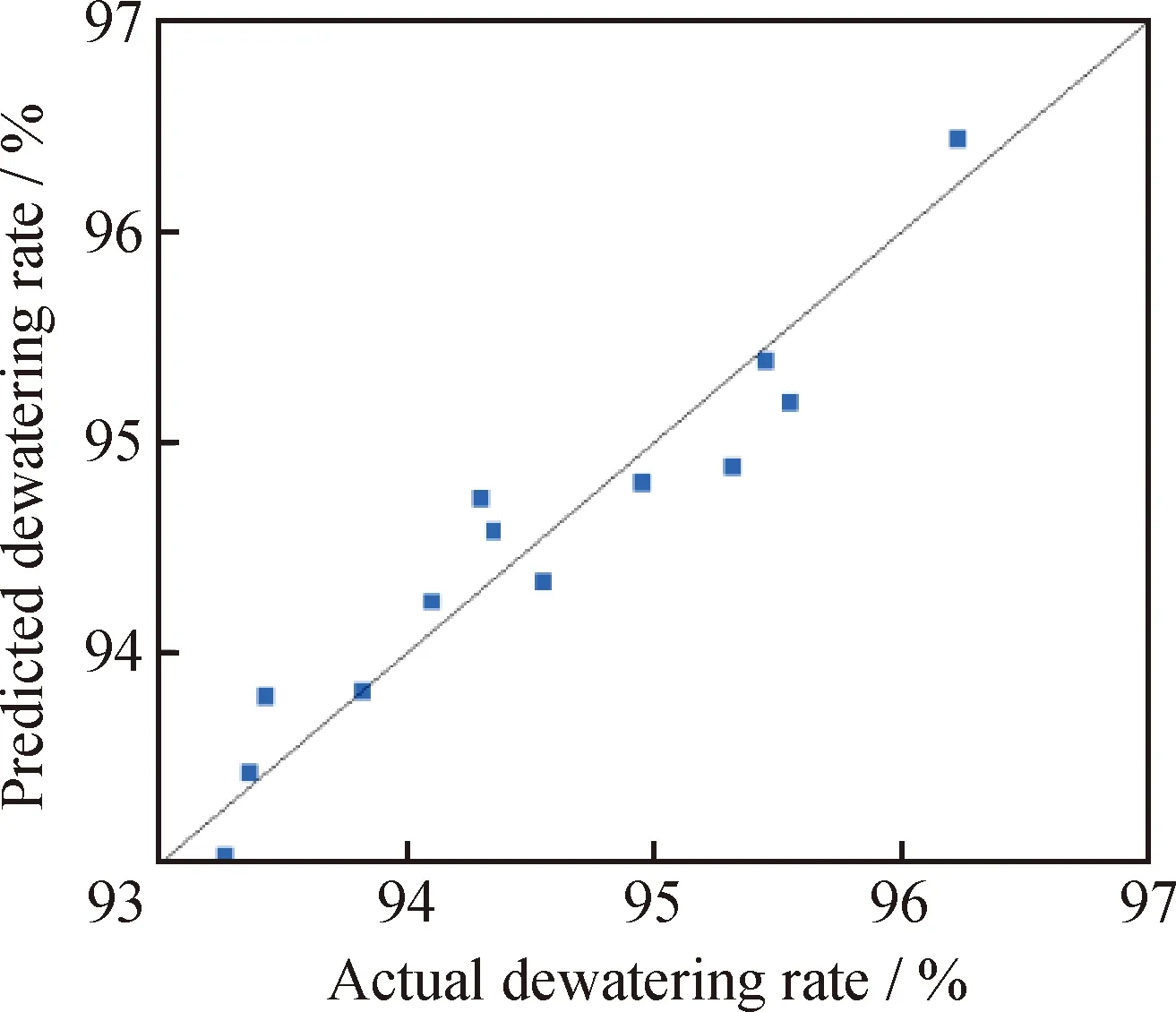
Fig.6 Comparison of the numerical calculated andpredicted dewatering rates
As shown in Table 3, the interactions between the major axisa1and the minor axisb1of ellipse 1 have a significant effect on the dewatering rate of the swirl device. When the major axisa2of ellipse 2 is 400 mm, the interactions between major axisa1and minor axisb1of ellipse 1 were analyzed by the response surface method. The contour map and response stereoscopic analysis results are shown in Fig.7. Increasing the length of major axisa1of ellipse 1 and decreasing the length of minor axisb1can improve the dewatering rate of the swirling device. When the minor axisb1of ellipse 1 is 90 mm and the major axisa1increases from 540 mm to 560 mm, the dewatering rate increases from 93.43% to 96.23%.
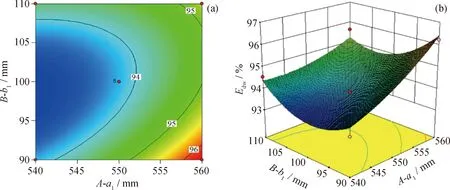
A and B are a1 and b1 coded referential symbols respectively. Edw—The dewatering rate;a1—The major axis of ellipse 1; b1—The minor axis of ellipse 1Fig.7 a1—b1 interaction effect on dewatering rate(a) The relationship between a1—b1; (b) a1—b1 interaction effect on dewatering rateCondition: a2=400 mm
3.2.2 Optimal structural parameters
The maximum dewatering rate of the cyclone unit is set as the optimization objective. The optimal results were obtained by solving and analyzing the response model. The numerical simulations of the double-ellipse tangent cone swirl device was carried out under the optimal conditions to verify the rationality of the response surface model. The conclusion is that witha1=560 mm,b1=90 mm,a2=409.96 mm, numerical calculated values is 96.23% and predicted dewatering rate is 96.65%. Under the optimal parameters, the deviation between the predicted and numerical calculated value of the cyclone device is small, and the maximum deviation of dewatering rate is 0.44%. Therefore, the optimal solution of the response model is reasonable.
3.3 Separation characteristics of coupling device
3.3.1 Pressure distribution
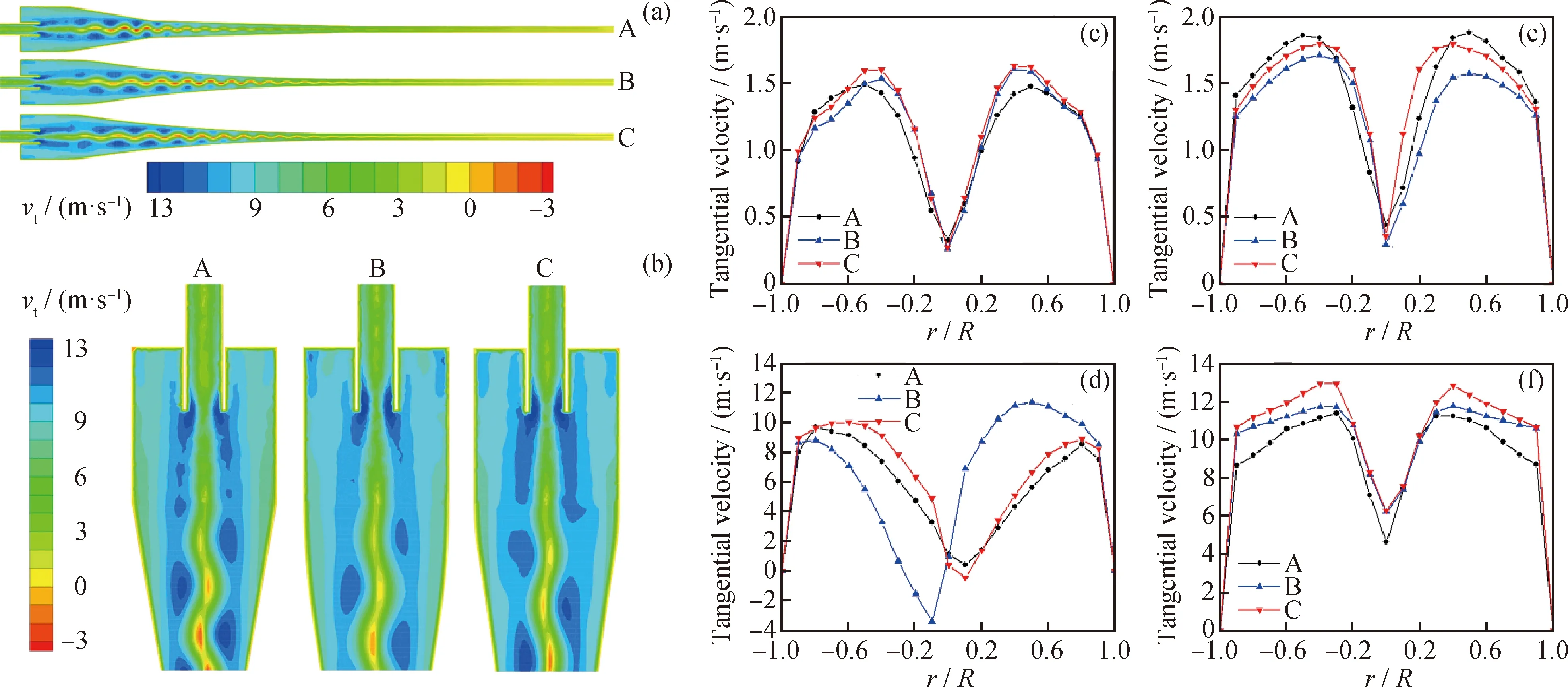
Pressure distribution affects not only the separation performance of the cyclone device, but also the flow field distribution inside the device[34]. The pressure distribution of different cone structures on thex=0 mm section is shown in Fig.8 (a) and (b). As shown in Fig.8(a), the maximum static pressure values of the three structures decreases with decreasing thez-coordinate value, which is because of the dissipation of turbulence energy. Obvious pressure gradients in the electric field region and the large cone end region of the three structures are evident, which are conducive to the oilwater separation of the emulsion in the swirling device. Fig.8(b) shows that the structure of the three kinds of static pressure distribution is almost the same, that is, the static pressure gradually decreases with decreasing the axial distance. A negative pressure area exists in the axial area of the overflow port. The optimized double-ellipse tangent type cone section of the structure of the negative pressure area is lesser, and the upward movement of the droplets is blocked, which will carry more capacity, that is conducive to the classification effect of the swirl device. Hence, the optimized double-ellipse tangential cone segment structure exhibits the better separation performance.
Fig.8(c)—(f) show the static pressure distribution curves along the radial direction of different sections (z=130, 680, 807, 850 mm) of the straight double-cone structure, the non-optimized double-ellipse tangent cone structure, and the optimized double-ellipse tangent cone structure. In the same section, the higher pressure and the pressure drop are more conducive to the separation of emulsion oil and water. As shown in Fig.8(c), the optimized double-elliptic tangential conical segment structure has a larger pressure and radial pressure gradient in thez=130 mm section. These findings indicate that the optimized double-elliptic tangential conical segment coupling device has a better separation performance. The double cone region of the hydrocyclone device is the main region for the hydrocyclone separation of the emulsion. As shown in Fig.8 (d) and (e), the pressure and radial pressure gradient of the double-ellipse tangent cone structure are relatively large in the sections ofz=680 mm andz=807 mm, which are conducive to the hydrocyclone separation of the emulsion, indicating that the optimized double-ellipse tangent cone structure has a better oilwater separation performance. Fig.8(f) shows that in 0<|r/R|<0.2, the reverse pressure value of the straight double-cone structure is higher than that of the optimized double-elliptic tangential conical segment coupling device, and the upward movement of the
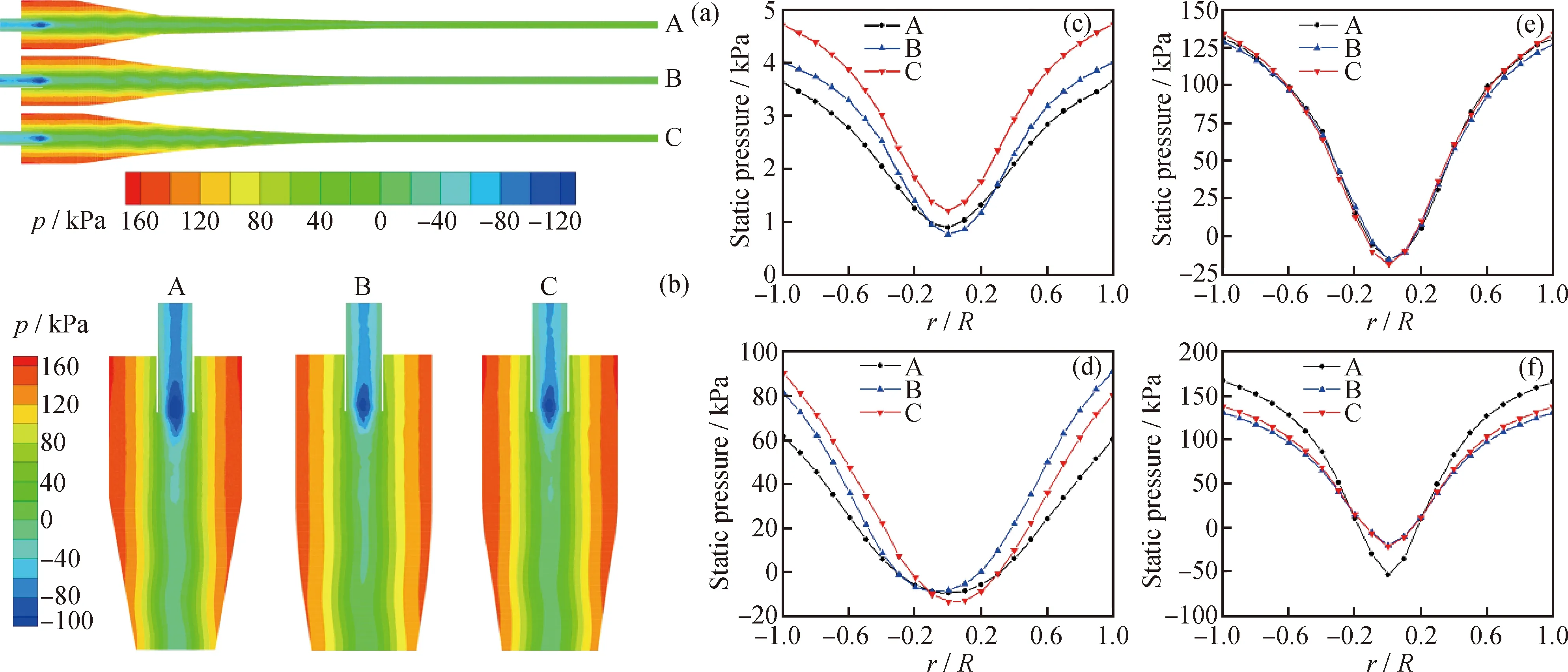
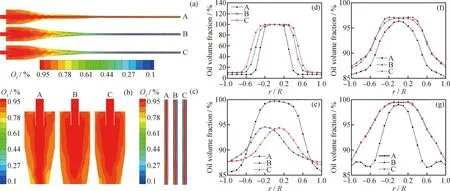
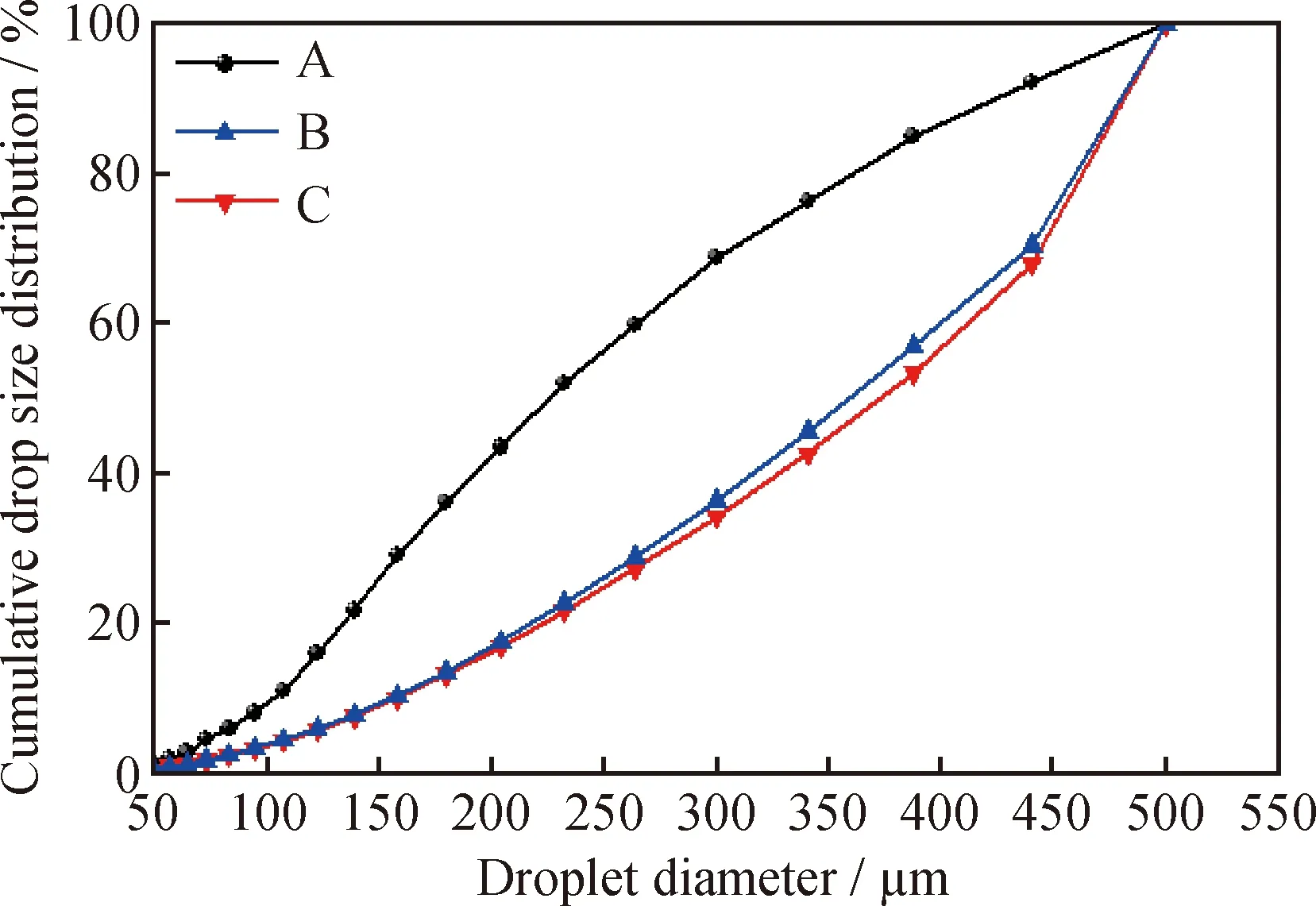
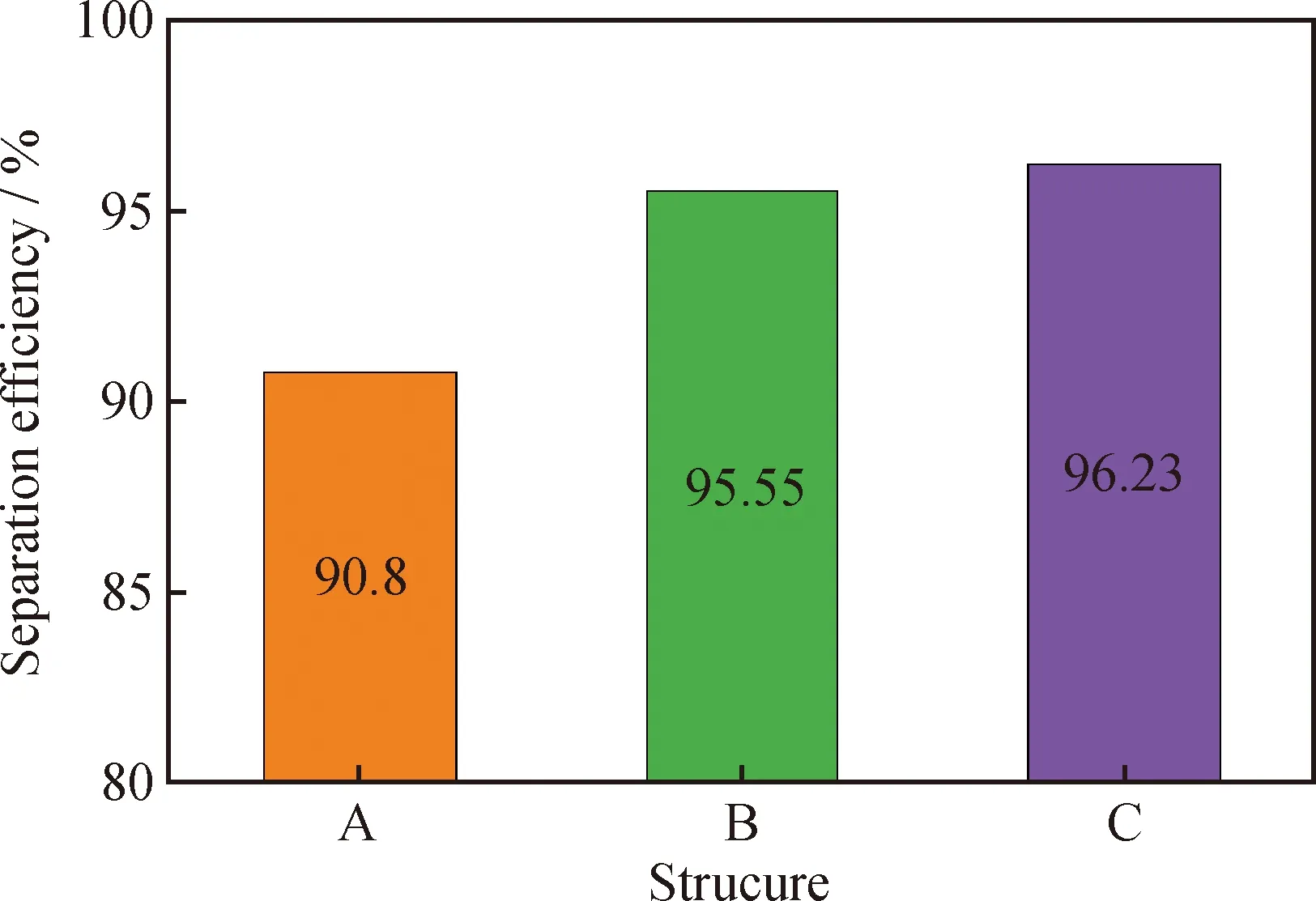
p is the static pressure,kPa;A—Straight double-cone structure;B—Non optimized double-ellipse tangent cone structure; C—Optimized double-ellipse tangent cone structureFig.8 Pressure distribution of different cone structures(a) Pressure distribution cloud diagram of different structures on the section x=0 mm;(b) x=0 mm and 750 mm liquid with higher oil concentration is blocked. Moreover, the optimized double-ellipse tangential conical segment structure has a better separation performance. Pressure drop is the most important parameter of pressure loss in the swirl device. The two pressure drops are as follows: The pressure drop between swirl device inlet and overflow port, that is, the pressure drop at the overflow port, and the pressure drop between the inlet and underflow ports, that is, the pressure drop at the underflow ports. The pressure drop at the overflow port is defined as: Δp1=pi-p1 (22) The pressure drop at the underflow port is defined as: Δp2=pi-p2 (23) Where,piis the pressure at the inlet port, Pa;p1is the pressure at the overflow port, Pa; andp2is the pressure at the underflow port, Pa. The pressure drop ratio (PDR) of the cyclone device is the ratio of Δp1and Δp2, which is: PDR=Δp1/Δp2 (24) The pressure drop of the underflow port is a quantitative parameter of the pressure loss of emulsion flowing through the cyclone device. The effect of different structures on the pressure drop is shown in Fig.9. The pressure drop of the overflow port with different structures is greater than that of the underflow port, that is, the PDR is greater than 1, which is consistent with the results reported by Chen et al.[35]. Moreover, the pressure drop of the underflow of the optimized double-ellipse tangential cone structure is 15.38% lower than that of the straight double-cone structure. The optimized double-ellipse connection is smooth, which reduces the vibration of the fluid. The energy loss of the emulsion passing through the double-cone section of the cyclone device is small, which is more conducive to the oilwater separation of the emulsion in the cyclone device. Therefore, the optimized double-ellipse tangent cone structure device is more conducive to oilwater separation of emulsion. A—Straight double-cone structure;B—Non optimized double-ellipse tangent cone structure;C—Optimized double-ellipse tangent cone structureFig.9 Influence of different structures on pressure drop 3.3.2 Tangential velocity distribution In the cyclone device, tangential velocity plays a decisive role in the centrifugal force. The greater the tangential velocity in the same section is, the greater the centrifugal force will be, which is conducive to the droplet migration to the wall of the cyclone device and to the cyclone separation of oilwater[36]. Fig.10 (a) and (b) show the tangential velocity distribution of different structures inx=0 mm section. As shown in Fig.10(a), the maximum tangential velocity values of the three results decrease with decreasingz-coordinate value. As shown in Fig.10(b), the tangential velocity distribution trend of the three structures in thex=0 mm section is roughly the same. The tangential velocity increases sharply along the radial wall from the axis center of the cyclone device. When the tangential velocity reaches the maximum, it decreases with increasing radius, which is consistent with the distribution of the combined vortex. After optimization, the tangential velocity of the double-ellipse tangent cone structure is relatively large, which is more conducive to the cyclone separation of emulsion. As shown in Fig.10(c)—(f), the tangential velocity distribution curves along the radial direction of the straight-plane double-cone structure, the non-optimized and the optimized double-ellipse tangent cone structures in different sections (z=130, 680, 807, 850 mm). As shown in Fig.10(c), in the section ofz= 130 mm, the tangential velocity of the double-elliptical tangent cone structure is greater than that of the straight double-cone structure, which produces greater centrifugal force and is more conducive to the separation of oilwater. Moreover, the maximum tangential velocity of the optimized structure is larger than that of the non-optimized structure, indicating that the optimized structure has a better separation performance. In the section ofz=680 mm, the maximum tangential velocity of the optimized double-ellipse tangent cone structure is higher than that of the traditional straight double-cone structure, which is conducive to the droplet migration to the wall of the cyclone device and the oilwater separation in Fig.10(d). These findings indicate that the optimized double-ellipse tangent cone structure has a better separation performance. The cone region is the main region of emulsion hydrocyclone separation, therefore, the maximum tangential velocity of the traditional straight double-cone structure and the optimized double-ellipse tangent cone end structure in thez=807 mm section are greater in Fig.10(e). The maximum tangential velocity of the traditional straight double-cone structure is greater, while the optimized double-ellipse tangent type cone section structure of tangential velocity with a better symmetric flow field is stabler. The optimized double-ellipse tangent cone section of the structure in the cone section area is smooth and connected. As shown in Fig.10(f), the tangential velocity of the traditional straight double-cone structure and the optimized double-ellipse tangent cone end structure in thez=850 mm section are basically the same. In conclusion, the optimized coupling device with double-elliptical tangent cone structure has a better separation performance. vt is the tangential velocity, m/s;A—Straight double-cone structure;B—Non optimized double-ellipse tangent cone structure; C—Optimized double-ellipse tangent cone structureFig.10 Tangential velocity distribution of different cone structures(a) Tangential velocity distribution cloud diagram of different structures on the section x=0 mm;(b) x=0 mm and 750 mm 3.3.3 Vorticity magnitude distribution Vorticity is an important index to measure the size of centrifugal force. At the same distance from the axis, under the condition of large vorticity, the faster the rotation speed of the droplet, the greater the centrifugal force, which is conducive to the droplet migration to the wall achieving efficient oil and water separation. The vorticity magnitude distribution of different structures in thex=0 mm section is shown in Fig.11(a) and (b) to further study the influence of different structures on the separation efficiency of emulsion. As shown in Fig.11(a), the variation trend of the vorticity magnitude of the three structures is basically the same. In the axial region of the cyclone device, the maximum vorticity first decreases and then increases with decreasingz-coordinate value, and the vorticity in the large cone region is relatively small. Based on Fig.11(b), the vorticity values of the three structures are larger in the axial region and smaller near the inner wall of the swirl device. In general, the vortex core is in the position of maximum vorticity. Therefore, in these three structures, the vortex core is in the center of the device. In the region of 750 mm Fig.11(c)—(f) show the radial vorticity magnitude distribution curves of the straight double-cone structure, the non-optimized double-ellipse tangent cone structure, and optimized double-ellipse tangent cone structure in different sections (z=130, 680, 807, 850 mm). As shown in Fig.11(c), in the cross sectionx=130 mm and in the inner cyclone region, the vorticity magnitude decreases sharply as it approaches the wall from the axial center along the radial direction. In the outer cyclone region, the vorticity increases slightly as the radius increases. However, near the axis, the vorticity magnitude of the double-ellipse tangent cone structure is larger than that of the straight double-cone structure. The vorticity magnitude of the optimized double-ellipse tangent cone structure is relatively larger, which indicates that the optimized double-ellipse tangent cone structure is better. As shown in Fig.11(d), the vorticity changes in the three structures are irregular in the cross section withx=680 mm. The direction of the vortex core deviates from the axis, and the flow field is vibrating. However, the vorticity of the optimized double-ellipse tangential cone structure is more symmetric, indicating that the flow field is stabler and is conducive to the oilwater separation of emulsion. The structure of the optimized tangential cone of the double-ellipse is better. The vorticity magnitude of the three structures in the section withz=807 and 850 mm is similar in Fig.11(e) and (f). In the axial region, the vorticity of the optimized double-ellipse tangent cone structure is slightly larger. The comprehensive analysis of the distribution of vorticity in the four sections of the cyclone device shows that the coupling device with the optimized double-ellipse tangent cone structure has a better separation performance. 3.3.4 Oil phase volume distribution Fig.12(a)—(c) shows the oil phase volume distribution of different structures in thex=0 mm section. As shown in Fig.12(a), in the cyclone device, the volume fraction of the oil phase gradually decreases along the direction of the decrease in thez-coordinate value, reaching the maximum near the overflow port and the minimum near the underflow flow port. Based on Fig.12(b), the volume fraction of the oil phase decreases with increasing radius, and a large amount of oil accumulates in the axial region, thereby promoting the formation of stable oil core in the axial region, which is consistent with the oil distribution law reported by Gong et al[37]. The higher the volume fraction of oil in the axial area is, the better the oil flow out from the overflow port and the higher the separation efficiency will be. The oil volume fraction of the double-ellipse tangent cone structure is larger in the axial region than that in the straight double-cone structure, which is more conducive to the discharge of oil from the overflow port (Fig.12(b)). The oil near the underflow port of the double-ellipse tangent structure is relatively less, which indicates that its separation efficiency is higher and its structure is more conducive to the cyclone separation of emulsion in Fig.12(c). Therefore, the double-ellipse tangent cone structure has a higher separation efficiency. Of is the oil volume fraction, %; A—Straight double-cone structure;B—Non optimized double-ellipse tangent cone structure; C—Optimized double-ellipse tangent cone structureFig.12 Oil phase volume distribution of different cone structures(a) Oil phase volume distribution cloud diagram of different structures on the section x=0 mm;(b) x=0 mm and 750 mm Fig.12(d)—(g) show the radial oil phase volume distribution curves of the straight double-cone structure, the non-optimized double-ellipse tangent cone structure and the optimized double-ellipse tangent cone structure in different sections (z=130, 680, 807, 850 mm). As shown in Fig.12(d) and (e), in the cross sections ofx=130 and 680 mm, the oil phase volume fraction of the double-elliptical tangent cone section is smaller than that of the straight double-cone section. Because the section is near the underflow port, the double-elliptical tangent cone section is more conducive to the cyclone separation and has a better structure. In Fig.12(f) and (g), the oil volume fraction of the double-elliptical tangent cone structure is greater than that of the straight double-cone structure in thex=807 and 850 mm sections. The volume fraction of oil phase near the axis of the double ellipse tangent cone structure is more than 95%, which forms a stable oil core. Because the section is near the overflow port, it is conducive to the discharge of oil from the overflow port, thereby increasing the separation efficiency. Therefore, the optimized coupling device with double-ellipse tangent cone structure has a better separation performance. 3.3.5 Droplet diameter distribution In the double-field coupling device, the oil and water in the emulsion are separated by the centrifugal force, the droplet size plays an important factor affecting the size of the centrifugal force[38]. Fig.13 shows the droplet diameter distribution of the double-field coupling device with three structures. From the figure, the optimized double-field coupling device′s droplet size distribution are shifted towards larger size, and the reason is that the optimized double-field coupling device has a smooth connection in the cone segment, which reduces the collision between emulsion and wall surface. These results indicate that the optimized double spherical tangent coupling device is more conducive to the coalescence of droplets, and the droplet is subject to greater centripetal force, which promotes the oil-water separation. 3.3.6 Separation efficiency As shown in Fig.14, the separation efficiency of different structures is calculated by the numerical simulations. The separation efficiency of the double-ellipse tangent cone structure is better than that of the straight double- cone structure, and the A—Straight double-cone structure;B—Non optimized double-ellipse tangent cone structure;C—Optimized double-ellipse tangent cone structureFig.13 Droplet diameter distribution underdifferent structures A—Straight double-cone structure;B—Non optimized double-ellipse tangent cone structure;C—Optimized double-ellipse tangent cone structureFig.14 Separation efficiency under different structures optimized structure is better than the unoptimized one. The double-ellipse tangent cone structure has smooth connection in the cone section, which makes the flow field stable and facilitates the oil phase to gather near the axis of overflow port. After separation, the water phase flows to the low flow port through the wall movement, which promotes the emulsion separation in the cyclone device. The pressure drop of the optimized double-ellipse tangent cone structure is smaller than that of the straight double-cone structure, and the energy dissipation of the emulsion in the swirl device is smaller. In the double cone region, it is also the main region of emulsion separation in the cyclone device. The maximum tangential velocity of the optimization double ellipse tangent cone structure on the same section is larger, which is conducive to droplet migration to the wall and oil accumulation near the axis. Second, the vorticity of the optimization double-ellipse tangent cone structure near the axis is relatively large, forming a vortex core, which is conducive to the oil coalescence near the axis of the cyclone device, making it flow out from the overflow port and improving the separation efficiency. The separation efficiency of the optimized double-ellipse tangential conical segment structure can reach 96.23%, which is 5.98% higher than that of the double-ellipse tangential conical segment structure (90.8%). In this study, a new type of cyclone device with double-ellipse tangent cone structure was proposed. The coupling simulation model of the electric field and cyclone centrifugal field was established. Moreover, Box-Behnken factor design and response surface methodology were used to optimize the double-cone structure. The influence of double-ellipse tangent cone structure and straight double-cone structure on the internal flow field and separation efficiency was analyzed. The rationality of the simulation model was verified by the separation experiment. The numerical model can reasonably and effectively predict the separation performance of the coupling device. The separation efficiency of the optimized double-ellipse tangent cone structure is higher than that of the straight double-cone structure. In the same section, the optimized double-ellipse tangent cone structure coupling device has a higher tangential velocity, which is conducive to the oilwater separation. The oil phase volume fraction of the double-elliptical tangential cone segment structure is nearer the overflow port than 90%, and it is relatively small near the underflow port. The finding indicates that the separation efficiency is better. The separation efficiency of the optimization double-ellipse tangent cone structure can reach 96.23%, which is 5.98% higher than that of the straight double-cone structure. Moreover, under the same working conditions, the coupling device of the optimized double-ellipse tangent cone structure has a lower pressure drop and a smaller energy loss, which is due to the low dissipation of turbulence energy.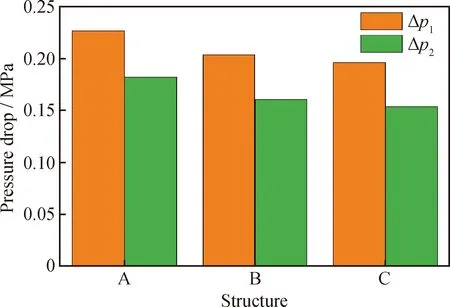
4 Conclusion
