黄土深基坑多支点排桩支护数值分析方法

2022-05-11邱本胜付一哲

山西建筑 2022年10期

邱本胜，付一哲

(1.武汉长江科创科技发展有限公司，湖北武汉 430014； 2.南水北调中线水源有限责任公司，湖北丹江口 442700)

1 概述

基坑工程发展的早期，基坑工程一般较浅，基坑结构设计主要以强度、稳定性控制为主，常规的计算方法便可以满足基坑设计的要求。但随着基坑开挖越来越深，基坑周围环境越来越复杂，对变形越来越敏感，采用多支点排桩支护成为深基坑支护的必然选择。同时黄土以其独特的自稳能力对基坑变形也有相当大的影响，因此，对黄土深基坑多支点排桩支护的变形研究有非常重要的意义。

常规计算方法模型假设：围护结构与支撑的连接方式为铰接，支撑和围护结构的变形分开计算，不考虑二者变形协调；土体对支护结构的侧压力在基坑开挖过程中保持不变，即土体的开挖、支撑的设置对侧压力的影响忽略不计；作用在支护结构上的土体达到了极限破坏状态。虽然这些假设对计算支护结构的内力影响不大。但在计算支护结构的变形时，这些假设明显不合理。

2 常规弹性支点法变形分析

弹性支点法将支护体系分解为竖向支护平面和支撑框架平面，并分别按平面问题简化计算[1]。首先在竖直平面内即基坑四周排桩中合理选取具有代表性的支护桩作为计算单元，所选计算单元一般位于坑边中间，此处基坑的空间效应小，变形最为显著，对基坑的计算具有代表性。然后将计算单元视作竖放的弹性地基梁，支撑结构视为弹性支座，坑外作用在支护结构上的土压力视为梁上的荷载，坑底以下土体对支护体系的约束视为随深度变化的弹性支座。最后将地基梁离散为有限个力学单元，研究各单元的性质，形成单元刚度矩阵。假定支护结构的水平位移采用抛物线位移模式，根据静力平衡条件、几何条件列方程计算出地基梁的变形。

(1)

(2)

其中，EI为排桩墙竖向计算宽度内的抗弯刚度；z为排桩顶点至计算点的距离；hn为第n个工况基坑开挖深度；y为桩墙计算点的水平变形；eai为开挖到第i工况时的主动土压力。

弹性支点法将支护体系分别简化为竖向支护面和支撑框架面，两面之间通过弹性支座反力建立联系。由于支撑框架面与竖向支护面分开计算，导致支撑体系与围护体系的变形不协调，而且受整个内支撑体系的整体结构布置即支撑点位移的影响，实际上并不存在各支点独自无关的支撑刚度。因此赋予所有支撑相同的刚度，必然导致计算结果与实际存在偏差[2]。

3 考虑桩间土刚度的有限元数值模拟

本文有限元分析采用商业软件plaxis，该软件是一种专门用于各种岩土工程问题分析的二维有限元软件。经常用于对基坑变形、路堤的沉降、堤坝的渗流等平面问题的分析[3]。plaxis能够模拟各种复杂的基坑平面形式，建模简单，单元划分灵活，能够快速生成有限元网格和计算结果；不必事先对支护结构背后的土压力做出假定，较好的反映了土体、围护结构、支撑三者之间的共同作用；能够对深基坑开挖过程中影响坑周土体移动的因素——地层特性、支护结构、分布开挖等进行模拟，能够较准确的模拟出坑周土体在基坑开挖、支护过程中的位移变化规律。

3.1 围护结构抗弯刚度的确定

多支撑支护体系支护排桩由众多单个钻孔灌注桩组成。平面分析时，为了简化起见，将桩间的土体看作是围护结构的一部分，其受力形式与内撑式地下连续墙类似。

围护结构在计算中按与桩墙抗弯刚度相等的原则进行等效替换，即所有围护结构计算单元的抗弯刚度相等。实际上围护结构不同位置计算单元的抗弯刚度是不同的，支护桩位置刚度大，偏离支护桩位置的刚度小，两桩之间的刚度最小。对围护结构进行等效刚度替换显然与实际有一定的出入，但是由于支护桩的桩距一般较小，对计算结果影响不大。目前工程上常将支护桩等价为一定厚度的壁式地下连续墙进行内力分析，简称等厚度法。

(3)

其中，h为连续墙的厚度；η为经验修正系数；D为支护桩的直径；L为桩间距。

等效抗弯刚度：

(4)

其中，b为单元的宽度，一般取单位宽度或者排桩的中心距；E为混凝土桩的弹性模量；I为截面惯性矩。

等厚度法是将支护桩的直径按照一定的经验系数进行折减，等价为一定厚度的连续墙，再按等厚度的多支撑连续墙模型进行结构计算。将支护桩替换为等效厚度的板进行计算，其基坑建模方便，计算简单。实践证明，在一般软黏性土地区，将排桩按等厚度的壁式地下连续墙进行设计，结果是偏于安全的。等厚度法认为排桩的抗弯刚度对围护结构的抗弯刚度起着决定作用，桩间土对围护结构的整体抗弯刚度没有贡献。这显然与实际是不相符的，土体具有一定的自稳能力，能够承担一部分水平荷载。完全忽略桩间土体对围护结构抗弯刚度的贡献将使围护结构的抗弯刚度偏小，尤其对自稳能力较强的黄土。

等厚度法是将排桩围护结构等效为厚度相当的连续墙，实质上是两者抗弯刚度的等效。仿照复合地基的竖向桩土应力分配法，针对黄土自稳性强的特性，本文探讨桩间土对围护结构刚度贡献的等效刚度分配法。刚度分配法将桩与桩间土看作整体，共同承受土体侧压力，整体等效刚度采用桩和土的刚度对等效板的贡献得到。等效刚度Esp：

Esp=mEp+(1-m)Es

(5)

(6)

其中，m为桩土分配系数；Ep为混凝土的弹性模量；Es为土的弹性模量；Ap为单桩的横截面积；A为相邻两桩直径与切线围成的矩形面积；D为桩的直径；d为桩间距。

等效抗弯刚度：

(7)

刚度分配法将桩土看作一个整体，桩间土的存在增强了整个围护结构的水平刚度，围护结构的刚度按桩土权重计算。

3.2 等厚度法和刚度分配法计算结果对比分析

为了分析两种计算方法对黄土基坑围护结构抗弯刚度的影响，取黄土的弹性模量为6.0 MPa，桩周土体为连续均质、各项同性材料。支护桩为混凝土钻孔灌注桩，支护桩的弹性模量为30 000 MPa，桩间距为1.5 m。围护结构抗弯刚度随桩径变化规律如图1所示。

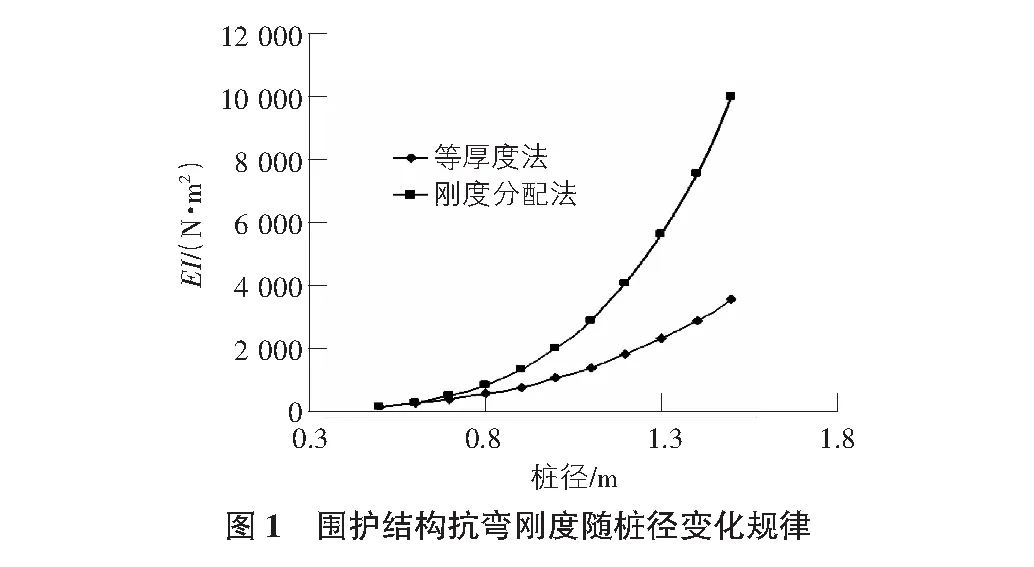
从图1中可以发现，桩间距一定时，围护结构的抗弯刚度随桩径的增加而增大，刚度分配法的计算结果大于等厚度法。桩径小于某一值时，两种方法的计算结果几乎相等。当桩径大于某一值时，刚度分配法的计算结果急剧增加，而等厚度法增加不大，几乎按原来的趋势线性增长。桩径较小时，桩间土所占的比例较大，土体对围护结构整体抗弯刚度的贡献较少，几乎可以忽略不计。在黄土地区，为了充分利用黄土的自稳能力，节约工程造价，一般桩间距与桩的直径之比为1.1～1.5，忽略桩间土体对围护结构整体抗弯刚度的贡献将使围护结构刚度计算结果严重偏小。因此，黄土地区基坑支护设计时，采用刚度分配系数法计算围护结构的整体抗弯刚度比较合理。

4 弹性支点法与有限元数值模拟对比分析

为了比较弹性支点法和二维plaxis有限元对基坑支护计算结果的影响，本文以西安地铁一号线万寿路地铁车站深基坑为例。该车站基坑为东西走向，基坑位于万寿路中央。基坑总长度为135.6 m，宽29.5 m，深度28.2 m。场地地貌属于浐河三级阶地，地下潜水埋深25.6 m～26.5 m。场地潜水活跃在冲积粉质黏土及其砂夹层中，该层土孔隙比较大，透水性好，富水性强。勘察基坑影响深度范围内的主要地层特征如表1所示。

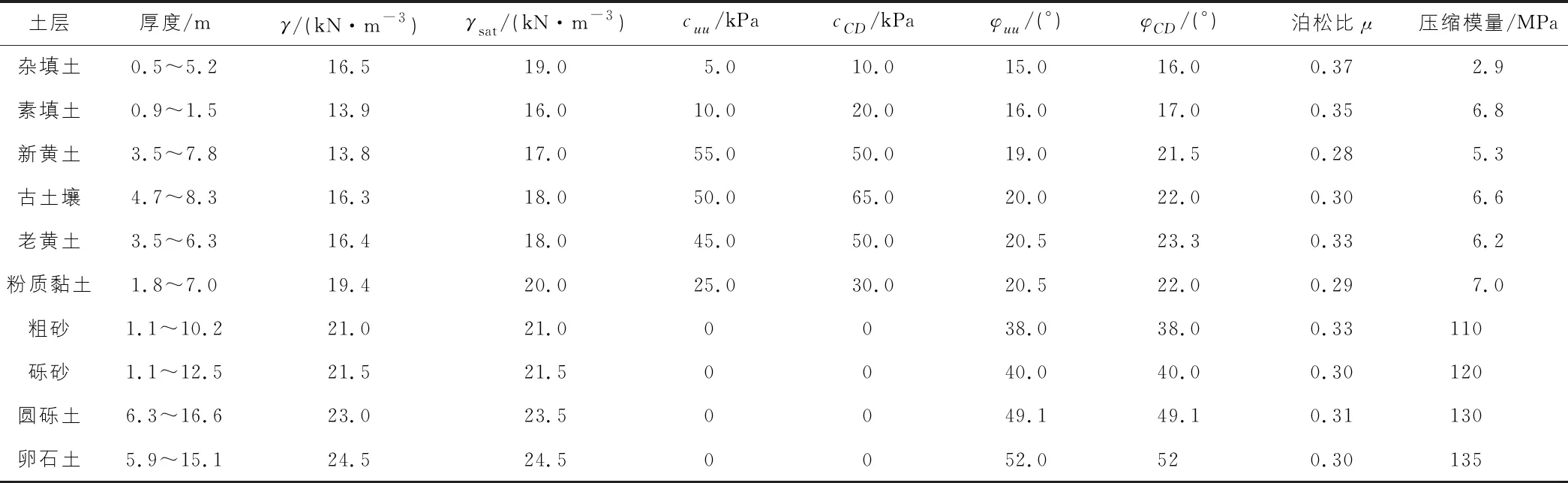
表1 各土层的物理指标

基坑支护采用钻孔灌注桩+内支撑的支护方案。支护桩直径1 300 mm，桩间距1 500 mm，嵌固深度10.0 m，自上而下设置五道水平横支撑，坑角处设置角撑。第一道支撑采用现浇800 mm×800 mm混凝土支撑，余下各道支撑采用直径600 mm，壁厚16 mm的钢管内支撑。第一道水平间距6.0 m，第二道～第五道钢支撑水平间距3.0 m。为了减少基坑周围地表的位移，从第二道支撑开始，对钢支撑施加预加轴力，依上而下，分别为200 kN，600 kN，600 kN，800 kN。

4.1 有限元数值分析模型

1)土体计算参数。

基坑周围土体的力学性质对基坑的稳定和变形产生重要影响。为此，合理确定土体的力学参数是有限元计算收敛的要点，也是模型能否真实模拟实际基坑的关键。本模型参数以基坑地勘报告为依据，适当参考临近成功基坑的参数。

2)支护结构参数。

支护结构参数见表2。

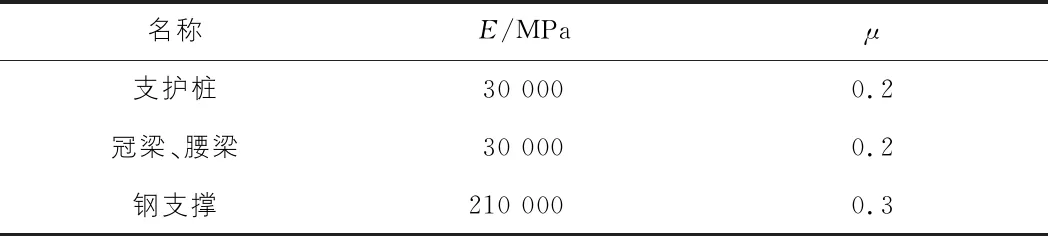
表2 支护结构参数

围护结构的等效板的抗弯刚度EI，采用等厚度法计算为1 489.0 N/m2，刚度分配法为4 069.9 N/m2，后者是前者的2.73倍。

4.2 数值计算结果分析

4.2.1 水平位移

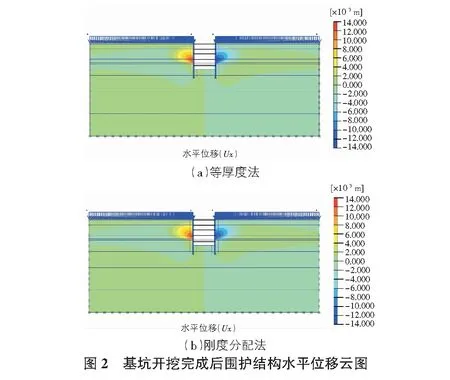
围护结构的水平位移随基坑开挖深度的加大而逐渐增大，当基坑开挖深度达到设计深度时，围护结构变形达到最大值(见图2)。

弹性支点法计算支护结构水平位移与实测结果吻合性较差，最大位移严重偏小(见图3)。忽略围护结构与土体之间的变形协调作用计算支护结构水平位移将使计算值失真。

plaxis有限元的计算结果与实测值接近，能够很好反映支护结构的变形，但是由于plaxis有限元为平面二维分析软件，无法模拟基坑的三维空间效应，使计算结果稍稍大于实测值，出于安全和工程上的精确性考虑，这种差值是允许的。刚度分配法的最大水平位移出现在第四道支撑附近，在这个位置以上，刚度分配法计算围护结构的水平位移更接近实测值，而在这个位置以下，采用等厚度法更加精确。从图1中分析得到，黄土基坑围护结构的刚度采用刚度分配法更接近实际值，理论上刚度分配法的计算结果更接近实测结果。但这没有考虑冠梁、腰梁对围护结构整体刚度的贡献以及预加荷载对围护结构位移的影响。因此，预加轴力、冠梁和腰梁对围护结构的位移影响亦是不可忽略的。

4.2.2 地表竖向位移

弹性支点法具有较强的经验性，认为地表的沉降是由于土体的侧向位移引起的，水平变形的体积与竖向变形的体积相等，同时假定地面的变形呈抛物线分布，地面沉降影响范围随开挖深度的增加而增加。

相对于弹性支点法，plaxis有限元能够较好描述基坑周边地面的沉降。越靠近基坑的地表，土体竖向位移实测值越接近刚度分配法，而远离坑边的地表，刚度分配法和等厚度法的差别不明显(见图4)。基坑开挖完成后地表竖向位移计算值与实测值如图5所示。

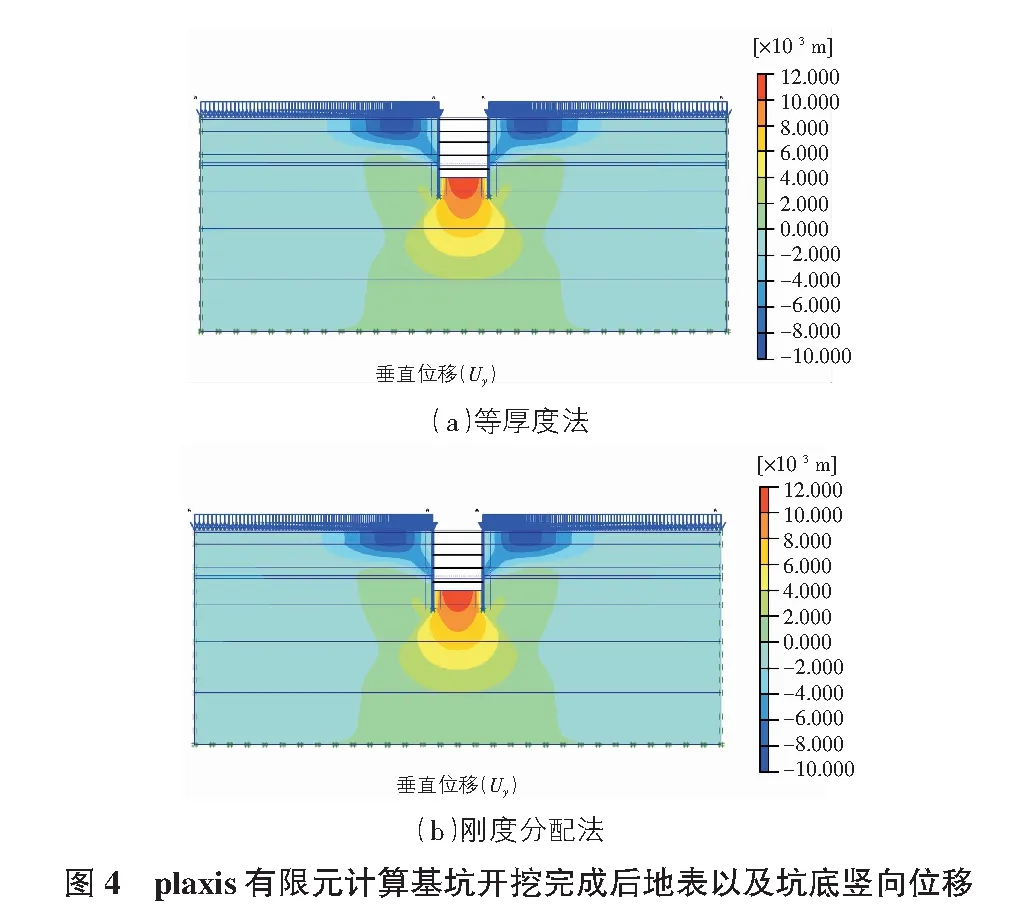
4.2.3 基坑隆起

土体隆起实质上是土体的一种滑裂失稳，土体抗剪强度越大，坑底的隆起量越小。弹性支点法对黄土地区基坑隆起没有专门涉及，只是根据软土的计算结果提供了一种供参考的经验法。认为坑底的隆起量与位置无关，每个位置的隆起量都相等。

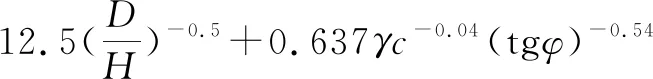
(8)

(9)

其中，δ为基坑底隆起量，cm；q为地面超载，kN/m2；D为支护结构的入土深度，m；c为土体的黏聚力。

弹性支点法计算的坑底的隆起量为17.2 mm，坑底处处相等，各部位计算值都较实测值偏大。弹性支点法提供的坑底隆起经验公式是根据软土的计算结果得到的，软土的强度小，土体强度对隆起的影响较小，可以忽略不计。而对于强度较大的黄土，不考虑强度因素对隆起的影响，计算值偏大。

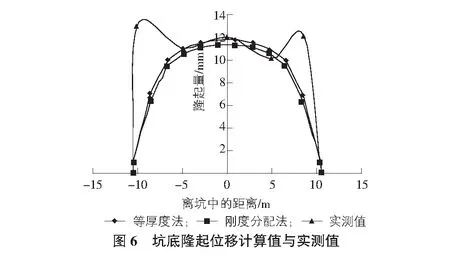
等厚度法和刚度分配法得到的坑底中间的区域隆起曲线与实测值能够很好吻合，但靠近坑边计算值则偏小较多，这是由于用plaxis对基坑进行模拟计算时，对围护桩以及桩间土进行整体假设，从而人为虚拟的增大了围护结构与坑底土体的接触面积，坑底土体与围护结构之间的摩擦力增大，导致靠近围护结构附近的土体隆起量减小，隆起曲线呈现中间大，两头小抛物线分布(见图6)。等厚度法和刚度分配法对坑底的隆起计算结果基本相同，这也反过来说明了围护结构的抗弯刚度对坑底隆起影响不大。