泛在电力物联网的网络安全提升研究
2022-05-11黄荷汤怡乾蒋代兴陈琳蔡立孔
黄荷, 汤怡乾, 蒋代兴, 陈琳, 蔡立孔
(1. 国网福建省电力有限公司, 福建, 福州 350001;2. 国网信通亿力科技有限责任公司, 福建, 福州 350001)
0 引言
随着泛在电力物联网的快速发展建设,电力物联网的源、网、荷、储之间的信息共享,相互服务的功能成为了当前网络建设的主要目标[1-4]。如何提高泛在电力物联网中网络抗攻击能力,对于降低电网的安全事故具有重要意义。
针对如何提高电网识别,检测和抵御恶意网络攻击的问题,越来越多的学者进行了研究。文献[5]提出虚假数据攻击会威胁到电网的状态估计,为此设计了一种虚假数据注入攻击方法,采用主成分分析方法将数据转换到高维空间,获取电网的近似结构矩阵,然后构造在线攻击,相比于传统的检测方法,该方法具有更好的检测精度。文献[6]提出了电网虚假数据注入攻击的非线性分析模型,在GAMS上编程,采用BARON求解,能够有效检测到注入的虚假恶意数据。文献[7]针对存在异常值的时候,采用基于鲁棒主成分分析的盲攻击方法,获取系统的攻击向量,注入的虚假数据仍然能被检测到。文献[8]基于状态估计方法,采用虚假数据注入攻击双层非线性优化模型,采用KKT(Karush-Kuhn-Tucker)方法将其转换成单层非线性问题,该方法可以提高状态估计的可靠性。本文提出了采用机器学习方法对虚假数据注入进行攻击检测的方法。
1 泛在电力物联网
泛在电力物联网指的是数采集的数据来源广泛存在于电力网络当中,通过末端感知节点[9-10],将电网中的用户数据、电力企业的数据、天气情况、电力市场价格等众多信息上传给上位系统[11-12]。泛在电力物联网的结构[13-15]如图1所示。
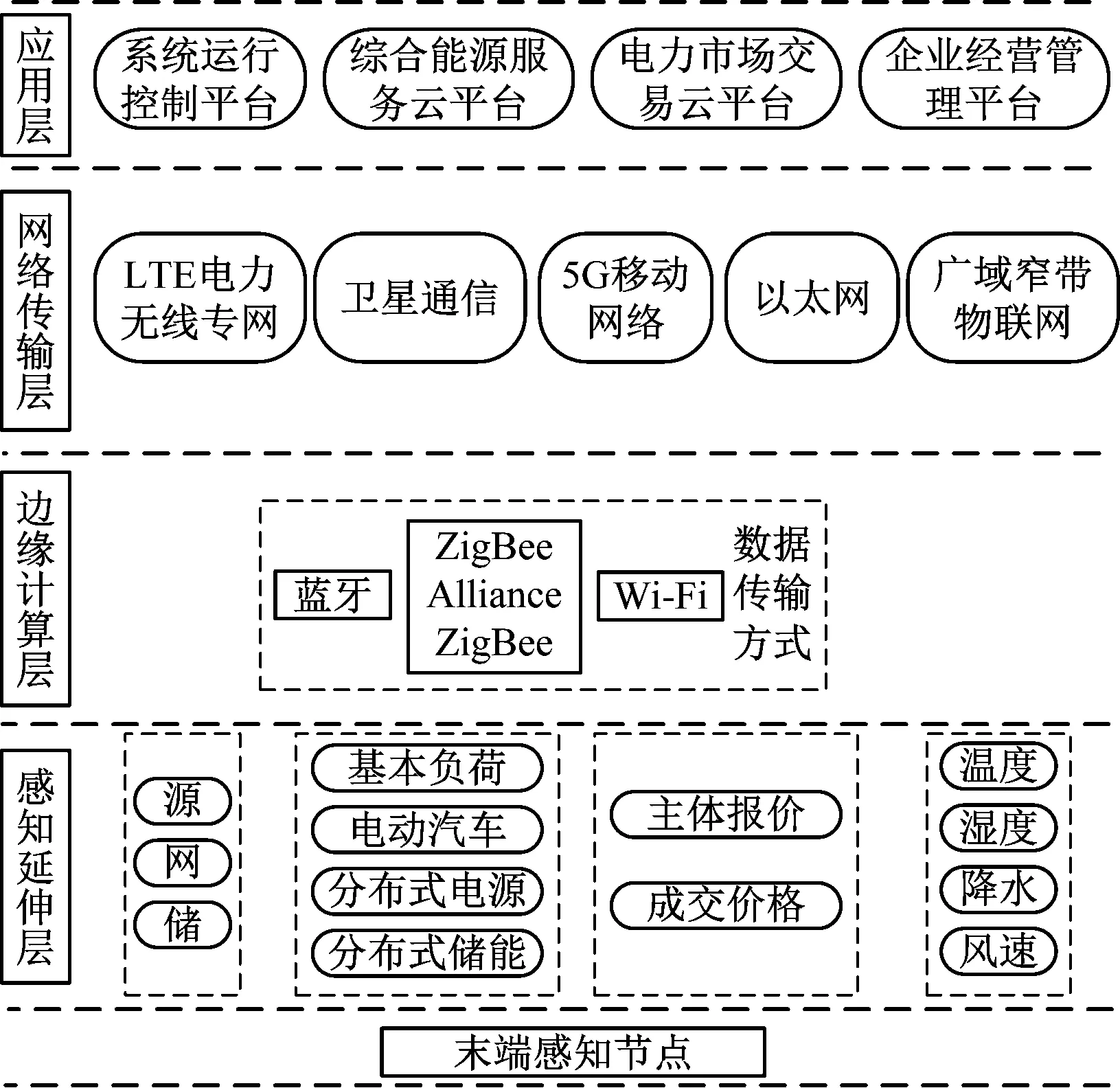
图1 泛在电力物联网基本架构
2 基于机器学习的虚假数据注入攻击检测
2.1 虚假数据攻击机理
在对直流系统进行状态估计的时候,令x为待估计状态变量,e为测量误差,则状态估计模型表示为式(1):
z=h(x)+e,z=[z1,z2,…,zn]T
(1)
式中,h(x)表示z和x为非线性关系。当忽略电阻,电压幅值为1的时候,式(1)可以写成式(2):
z=Hx+e
(2)
其中,H是m×n的雅可比矩阵,z是测量值。根据式(3)的目标函数,求取使目标函数最小的x。
minf(x)=j(x)=(z-Hx)TW-1(z-Hx)
(3)
其中,W是测量误差对角矩阵。当采用最小二乘法求取式(3)的时候,存在式(4):
(4)
根据残差检测不良数据,残差r根据式(5)求取:
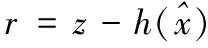
(5)
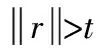
虚假数据攻击(FDIAs)的过程表示为设攻击向量为b,注入b之后得到的测量值zb如式(6):
b=[b1,b2,…,bm]T,zb=z+b
(6)
设c是攻击后对系统的干扰值,则残差表示为式(7):
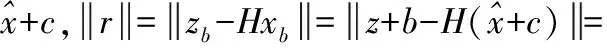
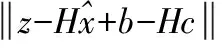
(7)
从式(7)可以看出,当b=Hc的时候,式(3)的求解结果为式(8):
(8)
则不良数据检测的参数如式(9):
(9)
当b=Hc的时候,篡改后的数据能使原本检测方法失效。当b=Hc的时候存在无数个解,增加了检测难度,则攻击者就可以随意改动电网数据。若攻击者能够控制H的时候,对电网的安全运行具有重大威胁。
2.2 基于PCA的数据特征提取
采用主成分分析(PCA)方法提取测量数据的主要特征。
设有N个样本,每个样本包含n个参数,表示为X=(xij)N×n。
(1) 对X进行标准化处理。
(2) 构建相关系数阵:R=(rij)n×n=X′X。
(3) 求取R的特征根和特征向量,λ1≥λ2≥…≥λn,则有
(10)
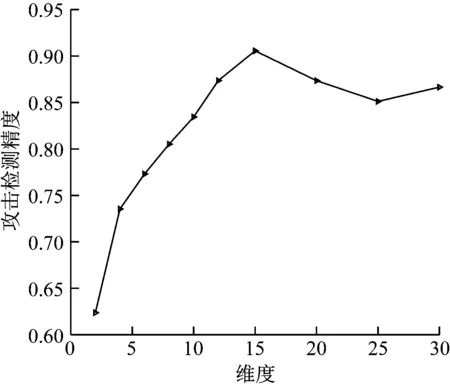
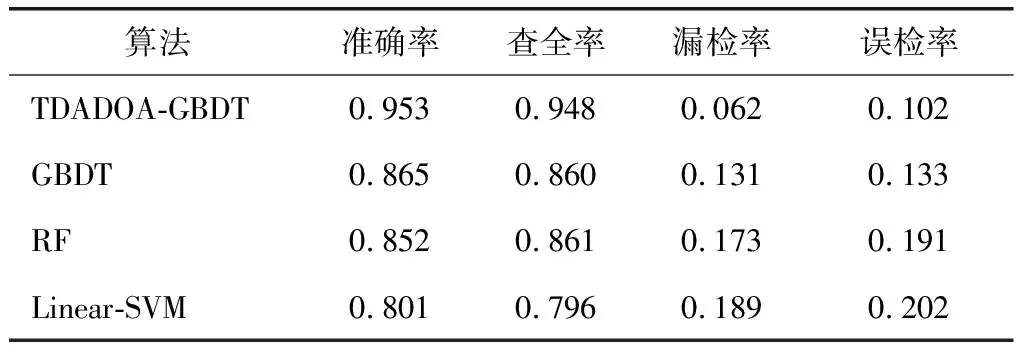
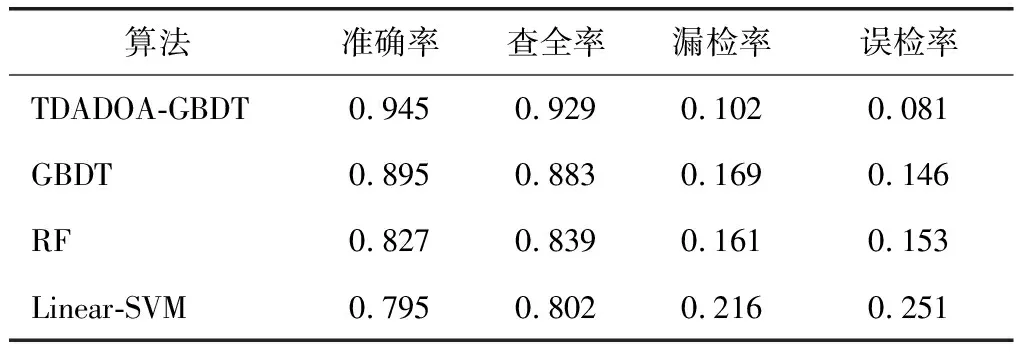
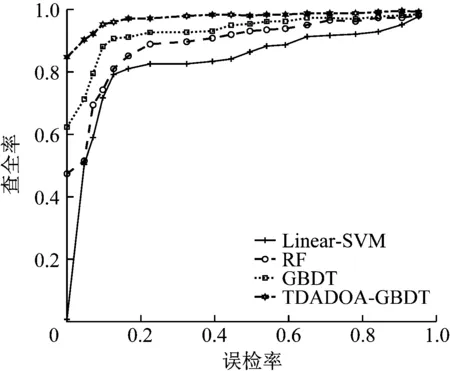
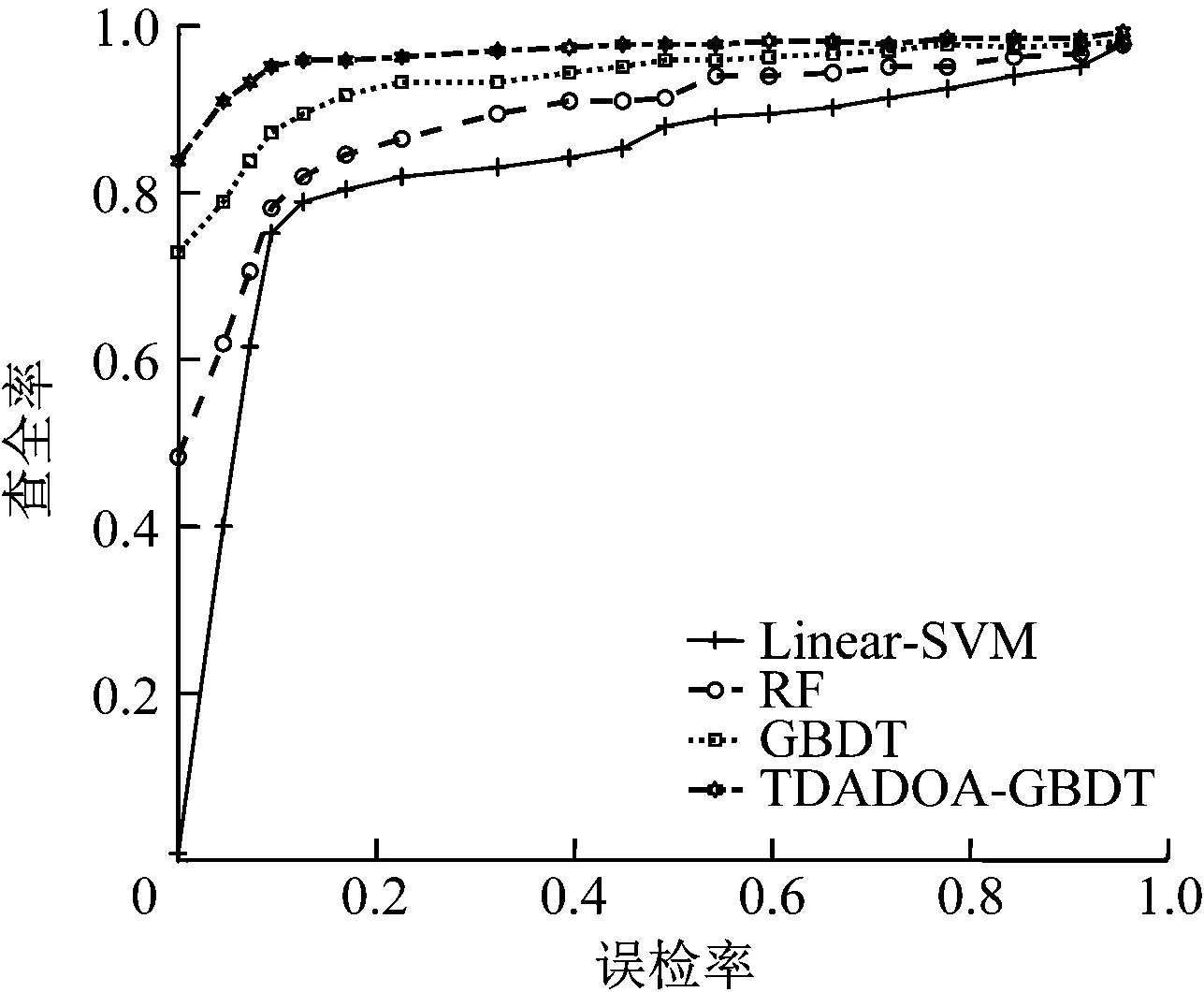
(4) 写出主成分,取m个参数代替原始数据(m Fi=a1iX1+a2iX2+…+aniXn(i=1,2,…,n) (11) XPCA=[F1,F2,…,Fm]=X[a1,a2,…,am] (12) (5) 计算每个参数主成分的贡献率: (13) 设数据样本为N,D={(x1,y1),(x2,y2),…,(xN,yN)},y∈{-1,1}。其中,X={x1,x2,…,xN}是攻击特征集,y是类标签。本文的目标是采用GBDT方法找到使x映射到y的损失函数L(y,F(x))最小,从而判断出系统是否受到虚假数据攻击[16]。 初始化基学习器F0(x)。攻击检测特征训练集D,损失函数L(y,F(x)),则使损失函数最小化的常数值β如式(14), (14) 定义损失函数为L(y,F(x))=log(1+exp(-2yF(x)))。 GBDT的过程如图2所示。 本文的虚假数据注入概率过程如下: (1) 令最大迭代次数为m。假设上一次循环损失函数极小值方向的残差为rim,则有 (15) (2) 残差作为决策树的输入。求取M棵决策树的叶节点区域Rnm,n=1,2,…,N,则有 图2 GBDT框图 (16) (3) 采用式(17)的方法确定最优步长βnm,极小化损失函数, (17) (4) 建立分类器Fboost(x),v∈(0,1],则有 (18) (5) 最终的梯度提升决策树模型表示为式(19): (19) Fboost(x)使虚假数据注入攻击检测模块,则数据受到虚假数据虚假数据攻击的概率及未受到攻击的概率表示为式(20): (20) 由于GBDT的参数会影响检测的精度,所以提出了采用三维自适应果蝇优化算法(Three-dimensional adaptive drosophila optimization algorithm, TDADOA)优化GBDT的网络参数。TDADOA的过程如下所述(见图3)。 (1) 设置最大迭代次数为Mg。果蝇群体数量Sp。初始位置X_axis,Y_axis,Z_axis。 适应度方差阈值μ,混沌迭代次数T。 (2) 果蝇寻找食物的公式如式(21)。其中,RandomValue为随机距离。 (21) (3) 果蝇与原点的距离为Disti,果蝇的味道浓度为Si,则有 (22) (4) 设适应度函数为Function(),味道浓度为Smelli,则有 Smelli=Function(Si) (23) (5) 将味道浓度最大的作为最优个体: [bestSmell,bestindex]=max(smelli) (24) (6) 求取味道浓度最大的果蝇位置,其他果蝇朝着该果蝇飞行: (25) (7) 求取平均味道浓度Smellavg、方差σ2: (26) (27) (8) 若σ2<μ且T>0, 混沌方程表示为式(28): xt+1=ωxt(1-xt) (28) 式中,xt∈(0,1] ,t是迭代次数。混沌搜索按式(29)进行: Cxt+1=4Cxt(1-Cxt) (29) 式中,Cxt∈[0,1]且Cxt≠{0.12,0.5,0.75}, (30) 将果蝇的位置Xi、Yi、Zi转换成混沌变量CXi、CYi、CZi。令T=T-1,且转至步骤(3)。 若不满足σ2<μ且T>0,则转步骤(9)。 (9) 执行步骤(2)~(8),直到达到最大迭代次数Maxgen,停止。 图3 算法流程 采用TDADOA-GBDT,线性支持向量机Linear-SVM,传统的GBDT和随机森林RF方法建立虚假数据注入攻击检测模型。硬件环境为Intel Core i7-7700HQ CPU,2.8 GHz,内存8G,64位操作系统,MATLAB 2017b。首先采用PCA方法提取电力量测数据的特征。然后采用TDADOA-GBDT方法在IEEE118-bus节点进行攻击检测。图4是采用PCA算法提取的特征数与查准率之间的关系图。 从图4可以看出,当采用PCA方法提取的特征维度为16的时候,检测精度最大,所以本文选取的特征维度为前16个指标。 分别采用LinearSVM、GBDT、RF和TDADOA-GBDT方法对IEEE-14系统和IEEE-118系统的量测数据进行攻击检测。IEEE-14系统的检测对比结果如表1所示。相应算法的ROC曲线对比图如图5所示。IEEE-118系统的检测对比结果如表2所示。相应算法的ROC曲线对比图如图6所示。 图4 不同维度下攻击检测精度 表1 IEEE-14系统检测结果对比 表2 IEEE-118系统检测结果对比 图5 IEEE-14系统ROC对比曲线 图6 IEEE-118系统ROC对比曲线 从图5和图6可以看出,在IEEE-14系统和IEEE-118系统中,在误检率相等的情况下,本文所提的TDADOA-GBDT的查全率均高于Linear-SVM、RF、GBDT算法,验证了本文所提方法具有更高的检测精度。 为了提高泛在电力物联网中的网络通信安全水平,提出了采用PCA方法获取影响数据攻击检测精度的主要特征元素,然后采用三维自适应果蝇优化算法对梯度提升决策树方法进行参数优化,采用改进后的算法对提取的量测数据进行分类处理,确定出攻击数据。相比于其他传统算法,本研究所提方法更适用于提高泛在网联网的通信安全水平,所提的TDADOA-GBDT方法由于存在算法优化过程,增加了计算时间,未来可以对算法的执行时间进行优化研究。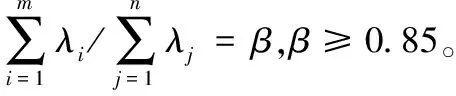
2.3 基于梯度提升决策树的攻击检测模型
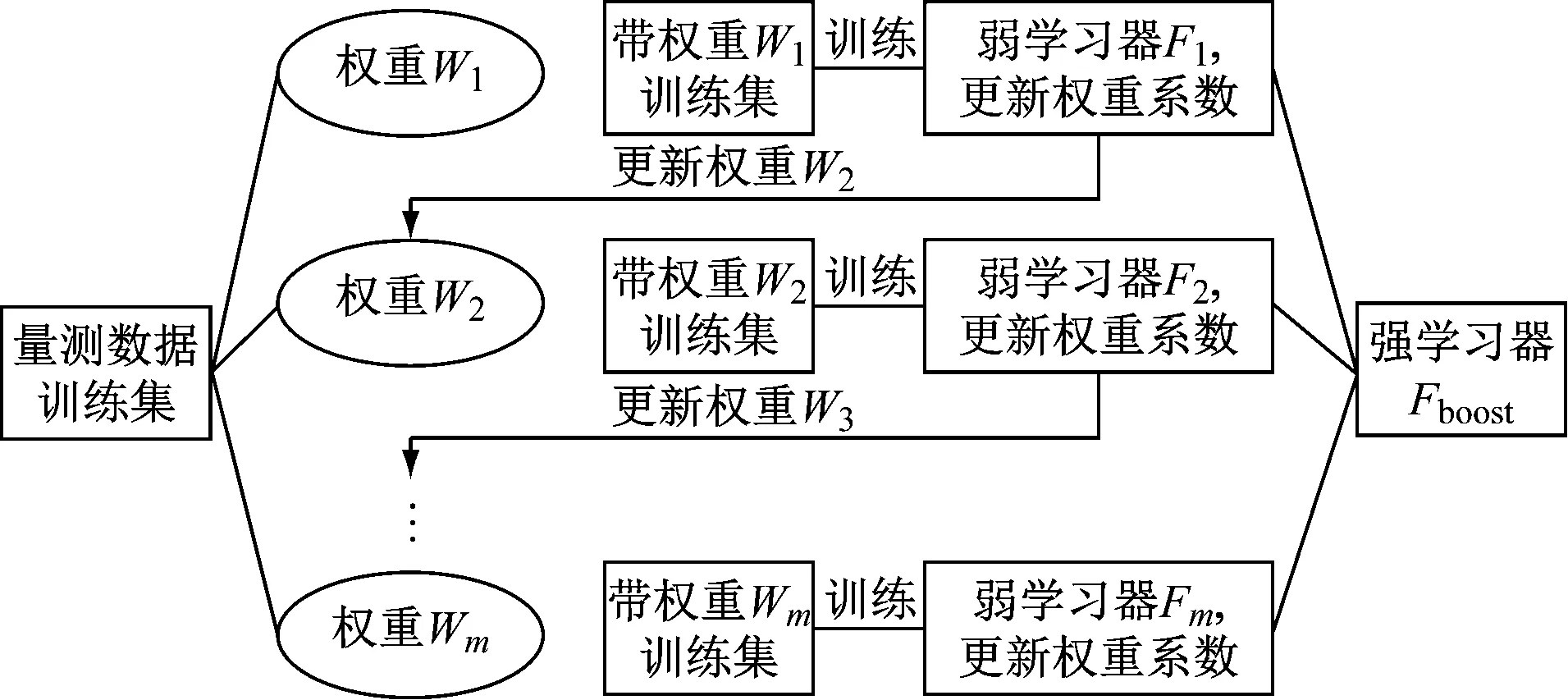
2.4 三维自适应果蝇优化算法
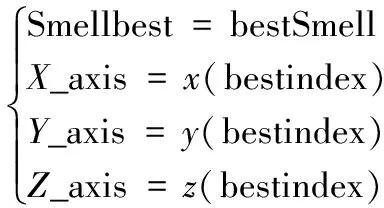
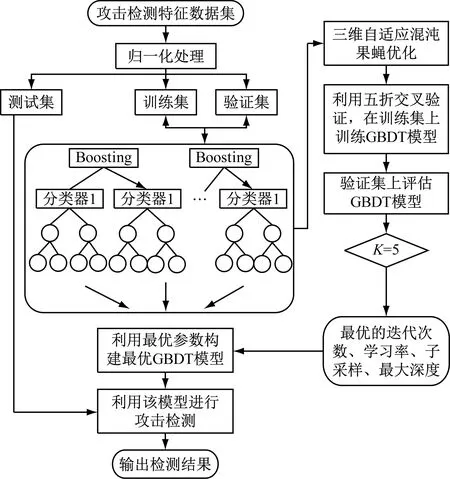
3 算例仿真
4 总结
