测量机器人在隧道监测中的应用分析
2022-05-11李由家单强英安平利冯明明史国辉
李由家,单强英,安平利,冯明明,刘 超,史国辉
(1.自然资源部第一大地测量队,陕西西安 710054;2.广州市天驰测绘技术有限公司,广东广州 510630)
1 引 言
目前,地铁隧道的监测手段主要有人工测量、自动化静力水准测量和测量机器人等。人工测量会产生人为照准误差,费时费力,而且夜间不能进行观测,出报表周期长;静力水准测量虽然能实现自动化,但是仅能提供高程沉降信息,存在一定的局限性;测量机器人则能提供高精度、高频率的三维坐标,广泛应用于自动化监测领域[1-4]。传统的隧道变形监测方法主要有测距仪法和全站仪法两种,但是这两种方法都具有明显的缺陷:一是监测点数量受到限制,不能全面反映出隧道整体的变形情况;二是监测周期相对较长,外业工作量大,获取的监测数据相对滞后;三是传统方法对作业环境要求较高。
相对于传统测量方法,测量机器人自动化测量具有操作简便、自动化程度高、工作效率高、精度高、非接触式等一系列优点[5-6]。贺磊等[7]介绍了测量机器人自动化实时监测隧道的要点,并对其监测成果进行了精度评估,验证了测量机器人自动化监测的精度;刘哲强[8]实现了测量机器人自动化监测成果的可视化输出,并对比分析了自动化监测成果与人工监测的精度,验证了测量机器人的可靠性;陈昊[9]验证了自动化监测系统在地铁隧道变形监测中的应用;何柯等[10]借助曲靖三清高速公路项目,对测量机器人监测系统在高速公路边坡的监测方式、数据传输处理方式、监测效果等方面进行了论述,为后期其他项目的建设提供了经验和技术指导;靳羽西等[11]基于多台测量机器人实现地铁隧道自动变形监测系统,该方法弥补了传统测量方法效率低、数据反馈滞后等不足,同时克服了一站式测量无法进行长距离地铁隧道监测的弊端,满足地铁隧道监测数据统一、实时、高效且高精度的要求。
本文以某临近地铁建筑基坑为例,采用测量机器人自动化监测系统对地铁结构整体变形情况进行监测,其结果可为同类型项目提供借鉴。
2 点位布设和监测系统建立方法
2.1 基准点、监测点布设
基准点的布设。地铁隧道内基准点布设于离开隧道两侧50 m以外且稳定的区域,监测区每端布设2组,对称分布于隧道两侧,各棱镜尽可能布设在较大的空间。
监测点的布设。每个监测断面上布设4个监测点,监测点棱镜安装在管片的两腰和道床两侧,且隧道布设的监测点不可影响行车安全。
2.2 监测坐标系统建立
完成基准点(串联基准点、普通基准点)和工作基点布设后,在正式开始测量前,还应建立监测基准。考虑本工程为监测基坑工作对隧道相对变形情况的研究,因此,监测坐标系统采用自由坐标系,坐标系的轴线与主要变形方向平行或垂直。
2.3 自动化监测系统的建立
项目监测过程中采用徕卡TM50型测量机器人及自动监测软件GeoMoS,对隧道进行实时自动化监测。徕卡TM50型测量机器人ATR自动照准精度为0.5 s,GeoMoS是由徕卡测量公司研发的自动化监测软件,其软件主要由监测器和分析器两部分组成。其中监测器已经拥有成熟的测量和计算程序,能为要求极高精度的应用提供理想的解决方案。TM50自动化监测系统的建立包括以下3个步骤:
1)系统架构。自动变形监测系统主要由数据采集、数据传输、系统总控、数据处理、数据分析和数据管理等部分组成。
2)系统调试。包括仪器通信调试和服务器稳定性调试。
3)获取监测点的初始值。系统通信调试完成后,人工操作测量机器人,依次测量各监测点,获取各监测点的学习点坐标,再通过自动化组网测量系统,采集不少于3 d的数据,取其平均值,作为各监测点初值。图1为自动化监测系统作业示意图。

图1 作业示意图Fig.1 Operation diagram
3 监测数据处理方法
3.1 沉降数据处理
通过自动化或人工监测得到各管片监测点的高程,再用高程计算各监测点沉降值。各监测点沉降量的计算公式如下:
ΔHi=Hi-Hi-1
(1)
式中:ΔHi为沉降值,Hi为第i次测量的高程,Hi-1为第i-1次的高程。
3.2 水平位移数据处理
通过自动化或人工监测得到各监测点的平面坐标,根据平面坐标变化得到隧道横向、纵向位移。各监测点的本次横向位移量为:
ΔXa=Xai-Xa(i-1)
(2)
各监测点的最近纵向位移量为:
ΔYa=Yai-Ya(i-1)
(3)
式(2)和(3)中:ΔXa为a点最近两次监测期的横向位移量,ΔYa为a点最近两次监测期的纵向位移量,Xai为a点第i次监测得到的X坐标,Xa(i-1)为a点第i-1次监测得到的X坐标,Yai为a点第i次监测得到的Y坐标,Ya(i-1)为a点第i-1次监测得到的Y坐标。
3.3 管片收敛数据处理
通过各监测点的三维坐标数据反算测点间水平、竖向距离,并与上次的测量值进行比较,其差值就是本期水平向、竖向收敛量,计算公式为:

(4)
D=Si-1-Si
(5)
式中:xa、ya、ha为监测点a的三维坐标信息,xb,yb,hb为监测点b的三维坐标信息,Si-1为上次测量隧道内径值,Si为本次测量隧道内径值,D为本次隧道收敛量。
4 实例分析
某临近地铁建筑基坑开挖深度为20 m,距离隧道水平位置最近为2.5 m,在基坑开挖施工过程中对地铁隧道结构产生影响,本项目对地铁隧道布设自动化监测系统和隧道结构进行监测,以保障地铁安全运营。
4.1 沉降分析
在基坑项目在施工过程中,采用测量机器人自动化监测系统对地铁结构整体变形情况和人工水准测量数据进行对比分析,沉降数据结果如图2、图3所示。
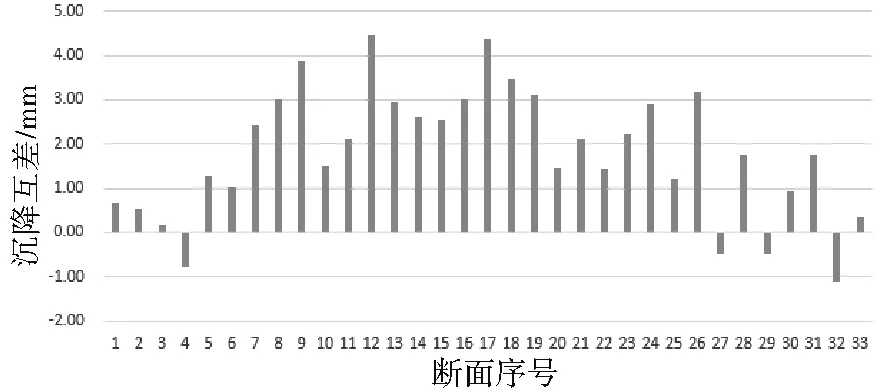
图3 人工测量与自动化测量沉降互差Fig.3 The mutual settlement difference between manual measurement and automatic measurement
由图2可知,基坑在施工过程中对临近地铁隧道道床造成了明显的沉降影响,人工测量和自动化测量均显示监测断面17为最大沉降量位置,人工测量沉降为29.75 mm、自动化测量沉降为34.18 mm,总体而言,人工测量与自动化测量的监测结果较为一致,沉降趋势相同。

图2 人工测量与自动化测量沉降累计量对比分析Fig.2 Comparative analysis of accumulated settlement between manual measurement and automatic measurement
由图3可知,人工测量与自动化测量沉降互差在5 mm内,其中监测断面12互差最大,为4.47 mm,全部监测点的整体平均互差为1.80 mm。表明自动化监测系统沉降监测结果与人工监测结果较为一致。
4.2 收敛分析
人工测量与自动化测量收敛累计对比和收敛互差对比分别如图4、图5所示。由图4可知,基坑在施工过程中对临近地铁隧道管片造成了一定的变形影响,其中变形最大位置是监测断面24,人工收敛为-22.30 mm,自动化收敛为-21.50 mm。总体而言,管片收敛效果人工测量与自动化测量具有较好的一致性。

图4 人工测量与自动化测量收敛累计量对比分析Fig.4 Comparative analysis of convergence between manual measurement and automatic measurement
由图5可知,人工测量与自动化测量收敛互差优于2 mm,监测断面27的收敛互差最大,为1.98 mm,整体平均互差为-0.39 mm,表明自动化监测系统收敛监测结果与人工监测结果较为一致。
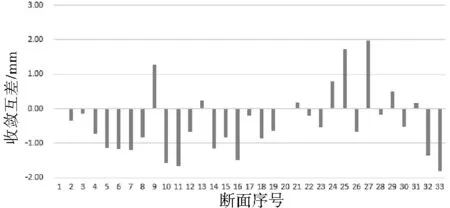
图5 人工测量与自动化测量收敛互差Fig.5 The convergence difference between manual measurement and automatic measurement
4.3 水平位移分析
人工测量与自动化测量水平位移累计对比和互差对比分别如图6和图7所示。由图6可知,基坑在施工过程中对临近地铁隧道造成了一定的水平位移影响,其中监测断面24的水平位移最大,人工测量水平位移为-5.70 mm,自动化水平测量位移为-6.23 mm。总体而言,隧道水平位移人工测量与自动化测量具有较好的一致性。
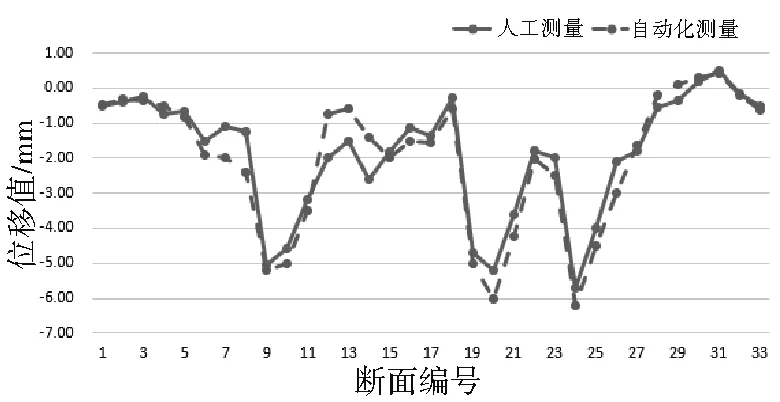
图6 人工测量与自动化测量水平位移累计量对比分析Fig.6 Comparative analysis of horizontal displacement accumulation between manual measurement and automatic measurement
由图7可知,人工测量与自动化测量水平位移互差优于1.50 mm,监测断面12的互差最大,为1.27 mm,整体平均互差为-0.14 m。表明自动化监测系统位移监测结果与人工监测结果较为一致。
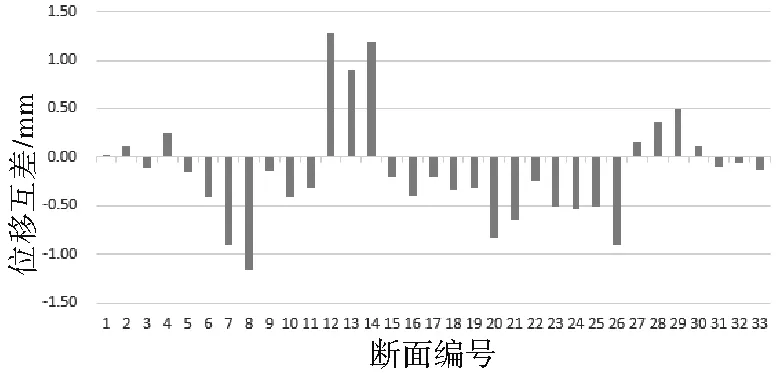
图7 人工测量与自动化测量水平位移互差Fig.7 The horizontal displacement difference between manual measurement and automatic measurement
5 结束语
本文基于测量机器人建立自动化实时监测系统,实现了地铁基坑工程多项重点监测项目的数据自动化采集、传输、处理以及发布。人工测量与自动化测量显示道床沉降最大分别为29.75 mm、34.18 mm;管片收敛变形最大分别为-22.30 mm、-21.50 mm;隧道水平位移量最大分别为-5.70 mm、-6.23 mm。人工监测与自动化监测对道床沉降、管片变形、隧道位移的平均互差分别为1.80 mm、-0.39 mm、-0.14 mm,上述结果说明自动化监测与人工监测结果较为一致,测量机器人自动化监测能够弥补人工监测的不足,但是监测成本较高,本项目监测成果可为今后类似基坑监测项目提供参考。
