基于GNSS数据的多源地质空间数据库更新模型效率分析

曹佳敏，卢春阳

(浙江省测绘科学技术研究院，浙江杭州 310000)

1 引 言

空间数据库模型是连接现实世界与空间实体的载体，主要是为了描述空间数据的组织关系，以便相关工作者掌握更多信息[1]。多源地质空间数据库存储着不同尺度以及不同格式的地质数据，包括地质矿产数据、地球化学数据以及地球物理数据等多源地质空间数据[2]。美国、加拿大和英国等一些经济较为发达的西方国家对多源地质数据库的研究起步较早，如美国地质调查局早在1960年就已经开始建设多源地质数据库。我国的地质资料数据库建设始于20世纪80年代中后期，虽然起步较晚，但在生态保护、资源审计、旅游资源调查等多个领域已取得了较大进展[3]。根据相关研究资料记载，目前对多源地质空间数据库更新模型与GNSS数据相融合的研究还不够全面，需要进一步探讨。基于上述背景，本文提出基于GNSS数据的多源地质空间数据库更新模型，首先设定两个空间直角坐标系，将地质空间数据进行空间坐标转换；其次，根据转换结果，划分多源地质空间数据集，并利用似真函数、支持函数与信任函数之间的关联，提取多源地质空间数据关联规则，基于GNSS数据构建数据库更新模型；最后进行该模型的效率分析，验证基于GNSS数据的多源地质空间数据库的更新效率。

2 基于GNSS数据的多源地质空间数据库更新模型

2.1 空间坐标转换

由于地质空间的特殊性，需要进行空间内坐标转换。根据建立坐标系的平行及重合条件，所建立的大地空间直角坐标系的各轴之间都是相互平行的关系[4]。在满足两个坐标系只有坐标原点不同的前提下，仅通过平移方式就能完成坐标转换[5]。设定O—ABC与O—A′B′C′为两个空间直角坐标系，两坐标系各轴之间相互平行，且坐标原点不重合。设定地面上任意一点J，则两坐标的形式表现为：

(1)

式中：p表示的是坐标系O—ABC的原点相对于坐标系O—A′B′C′原点的位置矢量，也就是空间内的3个平移转换参数。选取向量ΔA表示原始坐标系的坐标点与目标坐标系的相对位置向量，设定AZ、AW分别表示待求点在目标坐标系和原始坐标系的位置向量，如图1 所示。

图1 坐标转换示意图Fig.1 Diagram of coordinate transformation

从图1 可以看出，其坐标欧拉角与尺度因子的相对位置关系可表示为：

Aw=ΔA+(1+n)S1(SA)S2(SB)S3(SC)AZ

(2)

式中，ΔA表示两个坐标系之间的相对位置向量，SA、SB、SC表示坐标系的欧拉角，n表示尺度因子。在公式(2)成立的基础上，则得到用K和L所表示的单位矩阵，根据两个坐标系的欧拉角变换关系，转换公式(2)，得到：

Aw=ΔA+AZ+LAZ+nAZ

(3)

在进行空间数据生产、更新和应用时存在诸多影响因素，涉及空间基准与数学基础的差异，经过一系列计算，完成空间坐标转换[6]。

2.2 提取多源地质空间数据关联规则

多源地质空间数据库是获取其关联规则的主要研究对象，数据管理是关键部分[7]。针对地质空间的多源性特点，将多源地质空间的数据集按照数据集、要素类、要素集以及要素子集进行类型划分[8]。在多源地质空间数据库中，根据挖掘任务提取地质空间数据挖掘的目标数据集，缩小处理范围，提高挖掘效率[9]。在进行数据处理之前，需要对目标数据进行限制或者加以条件约束。设定A={a1，a2，…，am}是项的集合，另设任务相关的数据P为数据中要素的集合，其中每个R是项的集合，使R∈A；设Q是一个项集，要素集R包含Q，当且仅当Q∈R。设定关联规则Q∈A，其中Q∈A，B∈A，并且Q∩B=∅。数据关联规则的评价标准主要是支持度与可信度，其中，超过最低支持度阈值和最低可靠度阈值的规则称为强关联规则。用D(Q)表示数据中出现要素Q的概率，D(B/Q)表示地质空间D的数据中出现要素B的概率，公式表达如下：

Support(Q→B)=D(Q∪B)Confidence(Q→B)=D(B/Q)

(4)

根据交易集的要素特征，挖掘空间关联规则主要就是其支持度与信任度分别大于给定的最小支持度与最小信任度关联度原则[10]。其中，最小支持度表示项目的要素集在数学意义上的重要性，最小置信度表示关联规则的最低可靠性[11]。空间数据库与其他数据库的相同点是：都可以进行空间数据规则挖掘，但空间数据具有一定的空间特征，因此，需要更深入挖掘。首先，将空间数据进行组织划分，用不同的要素表达不同的数据特征[12]；其次，根据数据集所包含的空间对象的条件或者决策属性，进行离散化处理和关联规则提取，表达方式如下：

D1∧D2∧…∧Dn→L1∧L2∧…∧Lm(r%，e%)

(5)

式中：r%表示关联规则的支持度，D1，…，Dn表示空间数据的距离要素，e%为关联规则的置信度，L1，…，Lm表示空间数据的方位要素。

这种提取方式适用于多源地质空间的多维关联规则，通过设定一种具有逐层搜索的迭代方法，求得空间数据的支持函数和似真函数与支持函数在信任函数上的关系。设定一个非空集合2β，任意命题K在问题域中属于幂集 ，则其基本概率表示为j2β→[0，1] ，其中，j为基本概率分配函数，并满足j(∅)=0的条件，得出支持函数的表达公式为：

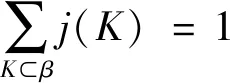
(6)

式中：j(K)表示命题K发生的信任程度，利用空间数据的证据体得到其信任函数的表达公式，用Bel(K)表示，即变量对命题K的支持程度与全部信任程度。似真函数的表达公式为：

Wl(K)=1-Bel(Kc) ∀K⊂β

(7)

式中：Wl(K)表示可能属于命题K的程度。根据上述公式，得出三者的关系，如图2所示。

图2 信任函数关系图Fig.2 Diagram of trust function

从图2可以看出，似真函数和支持函数与信任函数之间的关联，支持函数越大就表示获取该区域的数据关联规则越容易，反之则越难。至此，完成了多源地质空间数据关联规则的获取。

2.3 基于GNSS数据构建数据库更新模型

空间数据库的更新是将保存的某一时间点数据作为历史数据，以变化信息的方式更新数据库。更新过程是在原始数据库中增加实体的过程，在保存历史数据、维护数据层关系以及保证数据质量的基础上，进行空间数据库更新模型构建[13]。根据多源数据库的更新操作对象不同，多源地质空间数据更新可分为区域空间的实体整体更新与局部更新两种方式[14]。整体更新主要是采用数据集之间叠加的方式；局部更新主要是通过交互式空间实体图形变更来实现。二者的区别是局部更新的操作对象为单个实体，而整体更新的操作对象为多个实体[15]。空间关系分析与处理是实现空间数据库更新的关键，因此，需要将空间分析技术作为空间数据库更新模型的构建基础。同时，还需要考虑实际情况中的各实体之间的平面相邻、平面相离以及空间覆盖等情况。其中，由于覆盖情况比较复杂，需要对覆盖区进行具体研究。

设定线段HM和JM为原线段UP前进方向的左右两条覆盖区线段，原线段的起点U和终点P的坐标分别为(Ua，Pa)、(Ub，Pb)，覆盖区半径为r，则线段UP的左覆盖区线段HM的端点坐标为(Uc，Pc)、(Ud，Pd)，当Ub-Ua≠0时，l为线段UP的斜率，其计算公式如下：

(8)

当Pa-Pb>0，l>0或者Pa-Pb<0时，计算不同线段的斜率，得到线段覆盖区斜率，为空间数据库更新奠定数据基础。多源地质空间数据库的生产与更新主要是对同一地区但来源不同的空间数据进行有效处理，保证这些数据的属性以及几何位置层面都有对应的关系。基于上述描述与计算，空间数据库更新模型构建完成。

3 试验研究

3.1 地质空间数据组织关系分析

多源地质空间数据库中，通常都需要对相关信息进行定义与属性设置，包括数据的生产日期、数据名称等。数据属性越丰富，能提供的信息就越多，数据更新的速度就越快。某地质空间地层的数据属性如表1所示。

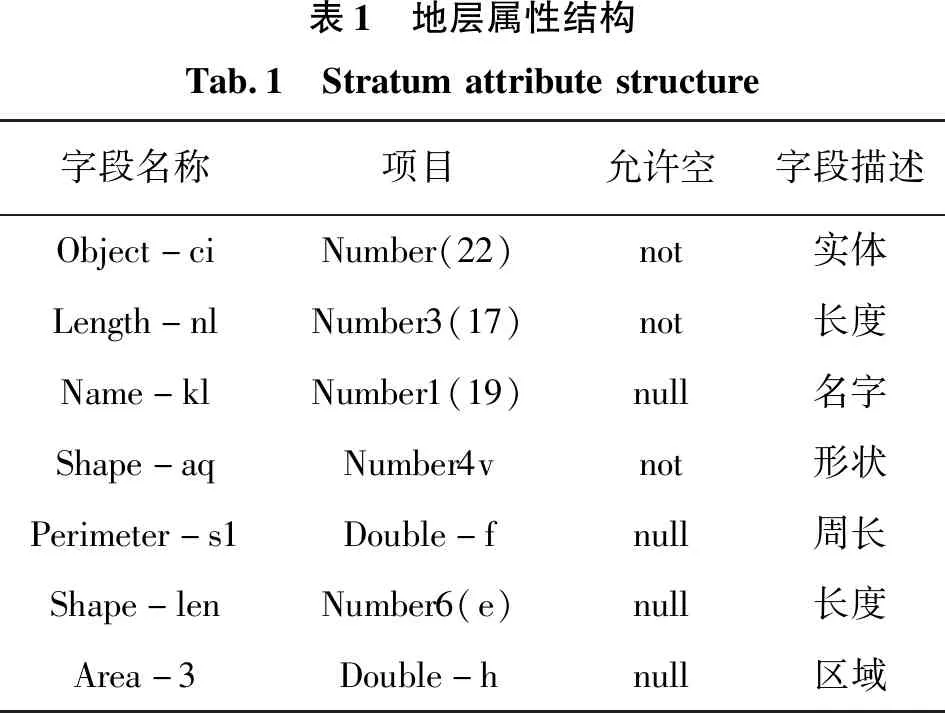
表1 地层属性结构Tab.1 Stratumattributestructure字段名称项目允许空字段描述Object-ciNumber(22)not实体Length-nlNumber3(17)not长度Name-klNumber1(19)null名字Shape-aqNumber4vnot形状Perimeter-s1Double-fnull周长Shape-lenNumber6(e)null长度Area-3Double-hnull区域

表1提供的地层属性结构信息，主要负责用户的数据信息查询以及空间数据组织关系分析。根据相应地质矿产数据、地球物理数据、地球化学数据以及遥感影像数据的数据集、要素集和要素子集得到多源地质空间数据组织关系，如表2所示。

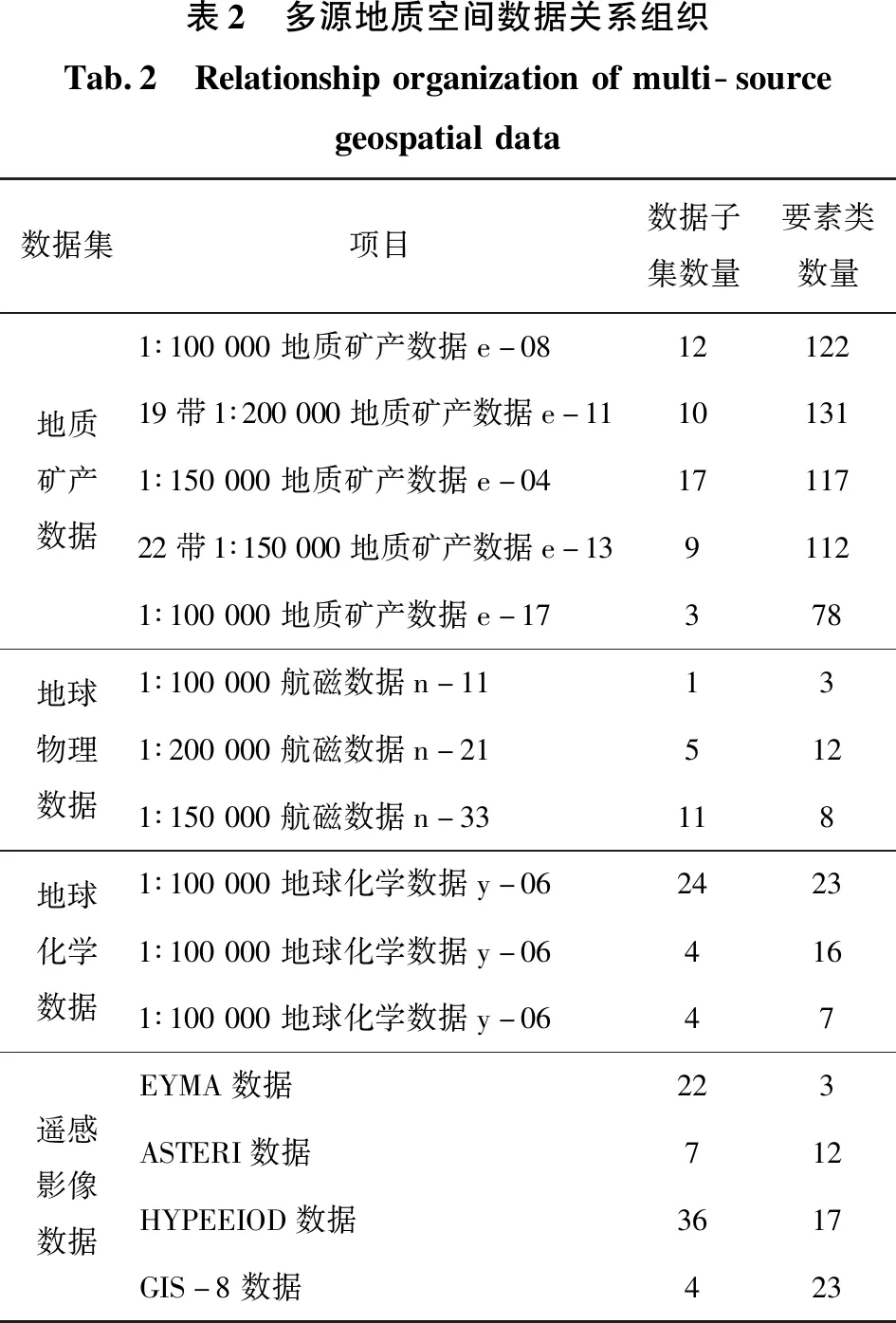
表2 多源地质空间数据关系组织Tab.2 Relationshiporganizationofmulti sourcegeospatialdata数据集项目数据子集数量要素类数量地质矿产数据1∶100000地质矿产数据e-081212219带1∶200000地质矿产数据e-11101311∶150000地质矿产数据e-041711722带1∶150000地质矿产数据e-1391121∶100000地质矿产数据e-17378地球物理数据1∶100000航磁数据n-11131∶200000航磁数据n-215121∶150000航磁数据n-33118地球化学数据1∶100000地球化学数据y-0624231∶100000地球化学数据y-064161∶100000地球化学数据y-0647遥感影像数据EYMA数据223ASTERI数据712HYPEEIOD数据3617GIS-8数据423

根据表2可以得出整体性的数据库更新模型的数据组织关系，应用上述信息进行模型更新效率测试。

3.2 数据库更新模型效率分析

选取野外调查、遥感调查两种传统数据库更新模型，对此次构建的更新模型在不同比例尺地质空间的更新速度进行测试，并得出图3所示测试结果。

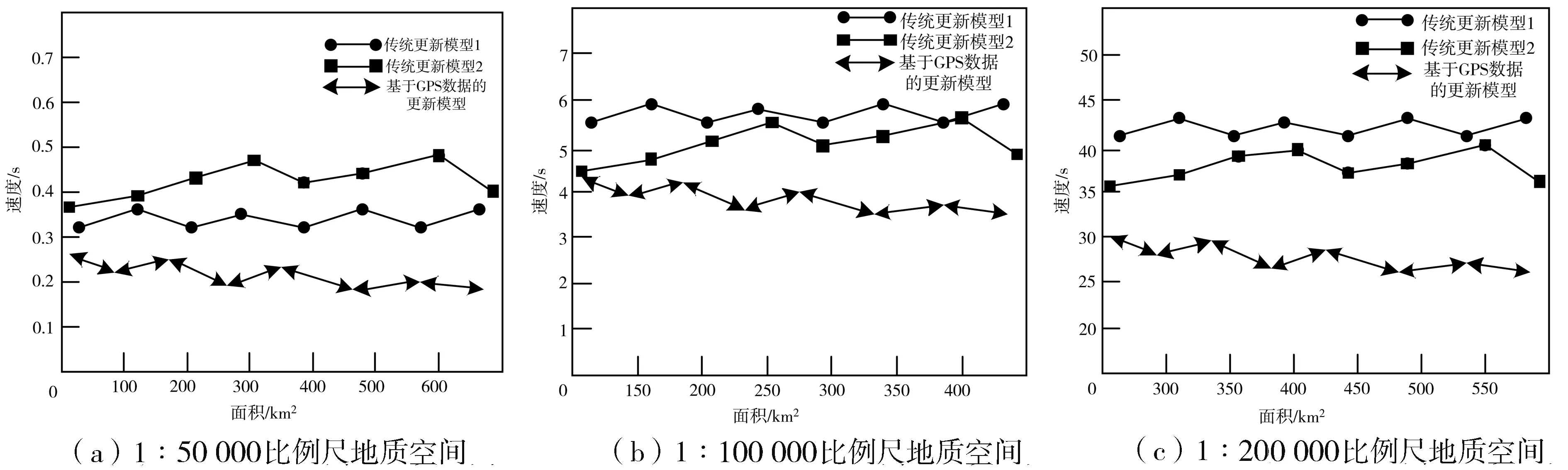
图3 数据库更新速度测试结果Fig.3 Results from database updating speed test

根据图3的数据模型更新速度测试结果，得出不同比例尺地质空间内3种更新模型的更新速度均值，如表3所示。

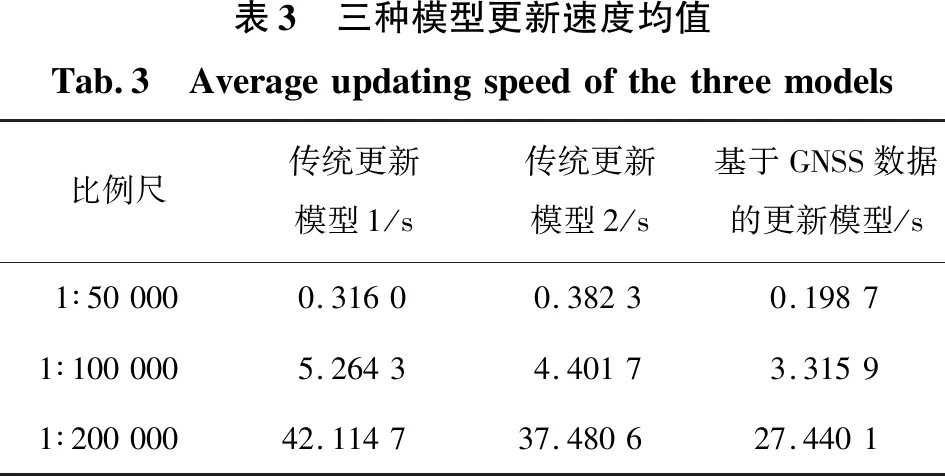
表3 三种模型更新速度均值Tab.3 Averageupdatingspeedofthethreemodels比例尺传统更新模型1/s传统更新模型2/s基于GNSS数据的更新模型/s1∶500000.31600.38230.19871∶1000005.26434.40173.31591∶20000042.114737.480627.4401

从表3可知，基于GNSS数据所构建的数据库更新模型在三种不同的比例尺地质空间的更新速度均高于两种传统数据库更新模型的速度。当比例尺为1∶50 000时，基于GNSS数据的更新模型比传统模型1高于0.117 3 s，比传统模型2高于0.183 6 s；当比例尺为1∶100 000时，基于GNSS数据的更新模型比传统模型1高于1.948 4 s，比传统模型2高于1.085 8 s；当比例尺为1∶200 000时，基于GNSS数据的更新模型比传统模型1高于14.674 6 s，比传统模型2高10.040 5 s。由上述内容可知，融合了GNSS数据的数据库更新模型的更新效率更高。

4 结束语

根据实验测试结果可知，本研究设计的数据库更新模型的数据更新速度快，更适用于研究多源地质空间数据库更新。其结果在一定程度上推动了数据库更新领域的发展，同时为学术界开展相关研究奠定了理论和实践基础。但是，由于研究条件有限，多源地质空间数据库更新模型的精度还有待研究，未来需要进一步探讨与完善模型精度。