厚尾相依面板序列均值变点的截尾CUSUM估计
2022-05-11杨银倩赵文芝
杨银倩,赵文芝
(西安工程大学 理学院,陕西 西安 710048)
0 引 言
1963年,统计学家Mandebortz发现,许多金融资产收益率分布具有厚尾特性,更适合使用厚尾模型描述金融数据[1]。由此,厚尾随机序列逐渐受到重视:ENGLE和BOLLERSLEV分别研究ARCH、GARCH模型[2-3];赵蕊等研究了GARCH(1,1)模型的多变点检验问题,基于SUPF检验统计量,在原假设下得到该统计量的极限分布[4]。随着对金融时间序列变点问题的研究逐步深入,具有P(|Y|>x)≈Cx-κ的厚尾时间序列成为热点问题,其中特征指数κ刻画了随机变量Y的尾部性质,反映金融资产未来可能发生的损失和风险,所以研究其变点的统计推断十分有必要。杨晓琴研究厚尾相依序列均值变点的检验问题,采用Block Bootstrap方法而非传统的独立同分布Bootstrap方法逼近统计量的渐近分布[5]。吕会琴等用ANOVA型检验讨论厚尾相依序列的均值多变点问题[6]。而在估计中,对所给序列建模时,必须估计变点时刻及跃度,否则容易对投资风险产生错误推断,从而造成不必要的损失。因此,分析厚尾序列的变点问题显得尤为重要。
上述对金融数据的研究主要在单一时间序列。随着社会经济的发展,金融数据量不断增加,大样本数据的变点问题引起了人们的兴趣。王慧敏等对高频数据下相依序列均值变点和方差变点问题,通过构造CUSUM型统计量理论推导出收敛速度[7]。张笛等在大样本数据场合,基于最小二乘估计研究方差变点问题[8],得到的结果比已有方法用时更短。时间序列数据经常因为数据单一导致实验结果误差较大,从此以后,面板数据变点问题逐渐受到学者们的重视。HORVTH等基于CUSUM方法,检验面板数据的均值变点[9]。SHIN等用CUSUM方法研究了面板数据的变点问题,检验了有限样本的面板数据的均值与方差变点,在原假设成立的条件下给出了均值变点检验统计量的极限分布与相合性[10]。刘鑫研究了面板数据中渐变变点的估计问题[11]。CHEN等使用CUSUM方法估计独立序列的面板数据的均值变点,得到了估计量的相合性和收敛速度[12]。王有为基于比值法估计了面板数据中均值变点个数[13];尉梦珂研究了面板数据变点模型的统计推断问题[14]。
但是,目前关于面板数据变点的研究多集中在薄尾情形,对具有P(|Y|>x)≈Cx-κ的厚尾时间序列变点问题则大多集中在单条时间序列上。本文研究该序列面板数据变点估计问题,考虑如下厚尾相依序列的面板数据均值变点模型:
Yit=Xit+μi(t),1≤i≤N,1≤t≤T
(1)
模型(1)中:∀i,{Xit}t=1,2,…,T是零均值的厚尾随机变量序列;每条序列均有共同的未知变点k0(1≤ko (2) 式中:μi1和μi2已知。 对于模型(1)的变点估计,大量学者做了相关研究:KOKOSZKA等研究{Xt}在方差有限情况下相依序列的均值变点估计问题[15-16];特征指数为1≤κ≤2时,KOKOSZKA等令{Xt}为零均值厚尾随机变量序列,在方差不存在的条件下,研究了{Yt}不含变点的均值变点估计[17];HAN等假设{Yt}存在一个均值变点,作出单条序列的截尾估计研究[18-19]。本文在文献[18-19]基础上,将其推广至面板均值模型中。由于方差不存在,因此无法直接利用Hjek-Rényi不等式,无法得出变点的相合估计[15-16]。所以,文中先对序列{Yit}截尾,使之在截尾情形下方差有限,并作出截尾条件下Hjek-Rényi不等式的证明,以保证变点估计一致性。 为方便研究面板数据变点截尾估计的相合性,提出假设条件和{Yit}的均值变点截尾估计。 假设1 ∀i,{Xit}t=1,2,…,T是严平稳的,具有n维对称的边缘分布并且满足 2μ(dx)=κ|x|-κ-1I{x<0}dx+ κ|x|-κ-1I{x>0}dx 式中:1<κ<2。 假设2 ∀y>0,t≠s,有 E[XitI{|Xit|≤y}XisI{|Xis|≤y}]=0 假设1是面板数据中厚尾分布应满足的条件,同时是n维边缘分布属于特征指数为κ的稳定分布的吸收域所满足的条件;因1<κ<2,可知Xit不存在协方差,因此假设Xit截尾不相关,假设2成立;假设条件3是指Tα→∞的速度比N→∞的速度快 ;假设条件4合理描述了N和(μi1-μi2)的关系。 (3) 式中:δiT为截尾参数,满足∀i,当T→∞时,有δiT→0,且aiTδiT→∞。对模型(1)的变点k0,在截尾情形下建立CUSUM估计量 (4) 其中 (5) 且 (6) (7) 证明 类似文献[13]的定理1证明思想,∀i,有T个随机变量M1,M2,…,MT,令 Bk={M1≤ε,M2≤ε,…,MT≤ε} 则 (8) 设 由式(8),有 其中 Bk′={M1≤ε2,M2≤ε2,…,Mk≤ε2} 因为 所以 由Karamata定理[20], 由此可得式(7)。 (9) 证明 对于模型(1), (10) (11) 当k=k0,有 (12) 由式(11)和(12)可以得到 (13) 由拉格朗日中值定理,有 (14) (1-τ0)1-γ-(1-τ)1-γ≥ (1-γ)(1-τ0)-γ(τ-τ0) (15) 联立式(13)、(14)、(15),可得 |E(Vk0)|-|E(Vk)|≥ (16) 所以 (17) 其中 (18) 由 (19) 得到 |E(Vk0)|-|E(Vk)|≤ (20) 联立式(17)、(20)可得 (21) (22) 由于 (23) 所以 (24) (25) 同样,对式(24)不等号右边的第二项,有 (26) 所以 (27) 若 (28) 则 (29) 有 (30) 则 (31) 因为0<γ<1,有 (32) (33) 利用假设3有 (34) 定理2得证。 推论1 在定理2条件下,如果∀i,当T→∞时,有δiT→0,且aiTδiT→∞,则∃0≤β≤1/2,C>0,使得∀ε>0,有 (35) 证明 由文献[13]推论1,aiT=O(T1/κ),δiT=O(T1/κ+β),得 (36) 在厚尾随机变量序列面板数据均值变点问题中,序列中“异常”点对估计结果是有影响的。本文将序列截尾,得到截尾序列情形下Hjek-Rényi型不等式,在此基础上证明得到面板数据均值变点估计的相合性,并表明了参数β的大小直接影响着变点估计收敛速度快慢。1 假设条件与截尾估计
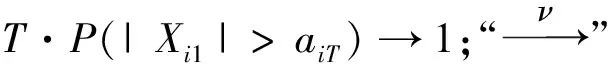
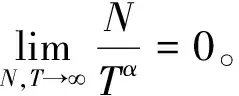
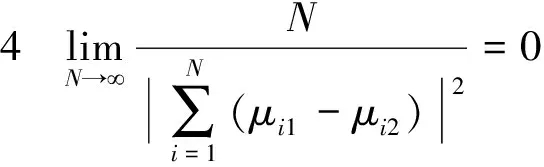

2 主要结果

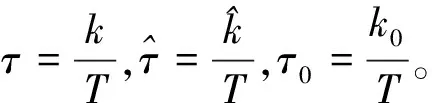
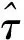
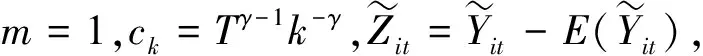
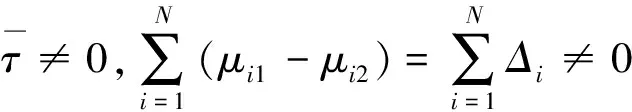
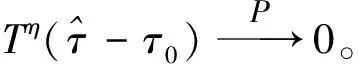
3 结 语
