强震作用下桩-土-断层非线性动力响应特性

冯忠居，关云辉，张 聪，蔡 杰，董芸秀，林路宇

（1.长安大学公路学院，陕西西安 710064；2.福建省交通建设质量安全中心，福建福州 350001；3.陇东学院土木工程学院，甘肃庆阳 745000；4.厦门路桥工程投资发展有限公司，福建厦门 361026）

引言

近年来，随着我国交通运输业的飞速发展，在强震区修建大型桥梁的情况越来越常见，桥梁桩基震害问题也因此时有发生［1］。桥梁工程受场地制约，存在位于近断层、跨断层的情况，此时近断层地震动产生的上、下盘效应、滑冲效应和显著竖向运动等特性［2］必须加以考虑。而以往设计基本是根据工程经验来确定断层的影响程度，显然不能很好的满足安全、经济的要求，故有必要对断层这一特殊地质条件下的桥梁桩基抗震设计展开研究。

国内外学者针对地震动作用下桥梁桩基非线性动力响应问题进行了大量研究。冯忠居等［3-7］通过利用大型室内模型试验与数值仿真，对不同强度地震动作用下断层-桩-土相互作用时桥梁桩基的动力响应特性进行了比较全面的分析。刘闯等［8-9］采用振动台模型试验，研究了跨断层不同类型地震动作用下桩基的桩身峰值加速度、桩身弯矩等动力响应特性。李雨润等［10-11］采用振动台试验分析了强震作用下桩基非线性动力响应规律，并对桩-土-结构动力相互作用理论模型研究现状进行了总结。凌贤长、Hokmabadi等［12-14］采用振动台模型试验和数值仿真，研究了地震作用下桩-土-结构的工作特性以及相互作用规律。李培振等［15-17］通过振动台试验与数值仿真，研究表明砂土层一般起放大作用，黏土层通常会产生阻尼效应。张素珍等［18］通过MIDAS/GTS有限元软件进行数值模拟，分析了水平地震动作用下单桩水平位移和弯矩的影响因素。鲍鹏等［19］利用时程分析法研究了刚性桩复合地基在不同地震作用下结构内力分布规律。熊辉等［20-22］通过建立有限元简化模型，对不同地震动作用下桩-土-结构的动力非线性时程响应规律进行了一定分析。

现有的研究成果多集中于强震作用下桩基非线性动力响应方面，而关于强震区近断层场地条件下桩基础动力响应的研究极少，关于地震荷载作用下近断层桩基础的动力响应特性的研究十分必要。文中通过MIDAS/GTS有限元软件，建立桩-土-断层共同作用模型，研究不同类型地震动作用下桩-土-断层非线性动力响应规律，以期为类似工程的抗震设计提供依据。

1 工程背景

海文大桥（原铺前大桥）跨越铺前湾—东寨港海域，桥址区存在22条断层，大桥走线共穿越3条断层，其中F2（铺前-青澜）断层为正断层，断层与桥位关系如图1所示。桥址区设防烈度为Ⅷ度，50年超越概率10%动峰值加速度为0.35 g。该桥桩基础建设环境国内外鲜有，桩基础抗震问题十分突出。

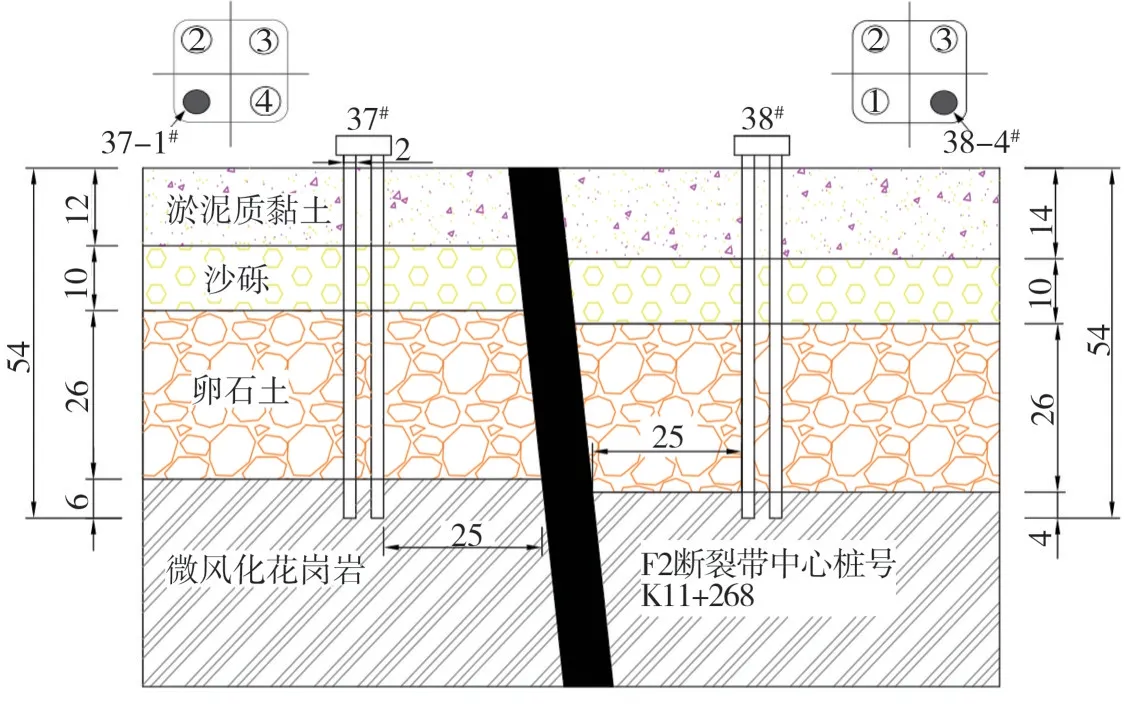
图1 断层与桥位关系Fig.1 Relationship between fault and bridge location（unit：m）

海文大桥37#墩和38#墩分别位于F2断层的下盘和上盘，均由4根桩长54 m、桩径2 m、桩间距为5.5 m的群桩组成，嵌岩深度分别为6、4 m。F2断层宽度约8 m，上下盘错落约2 m，37#和38#桩基础距断层25 m左右，海文大桥F2断层特征如表1所示。

表1 F2断层特征Table 1 F2 fault characteristics

2 数值仿真

2.1 模型建立与参数选取

考虑土体材料具有明显的非线性以及计算结果的准确性［18-20］，利用MIDAS/GTS数值仿真软件建立非线性模型，桩基和承台使用匀质弹性材料制作，制成的模型与原型相似，桩基周围的岩土体需要反映其塑性变形，故采用弹塑性模型，非线性分析计算利用摩尔-库伦屈服准则，使用位移收敛和内力收敛进行检验判断。

2.1.1 模型建立

模型尺寸为X轴方向100 m，Y轴方向62 m，Z轴方向82 m。土层分布为淤泥质粘土（夹砂）、黏土、砂砾、卵石土、中风化花岗岩和微风化花岗岩，其中其淤泥质黏土（夹砂）厚度为12 m（下盘）/14 m（上盘），黏土、砂砾厚度均为10 m，卵石土厚度为26 m，微风化花岗岩厚度为20 m。建立破碎带模拟断层作用，将地质条件简化为断层破碎带出露地表，对各层破碎带参数进行相应折减。桩周附近土体和断层破碎带网格加密划分，尺寸为1 m，外侧土体网格尺寸按1～4 m渐变。桩土接触界面采用MIDAS/GTS中的一般接触，采用自动接触的方式定义，法相切向刚度比例系数采用基本设置值。37#墩和38#桩墩模型如图2所示。

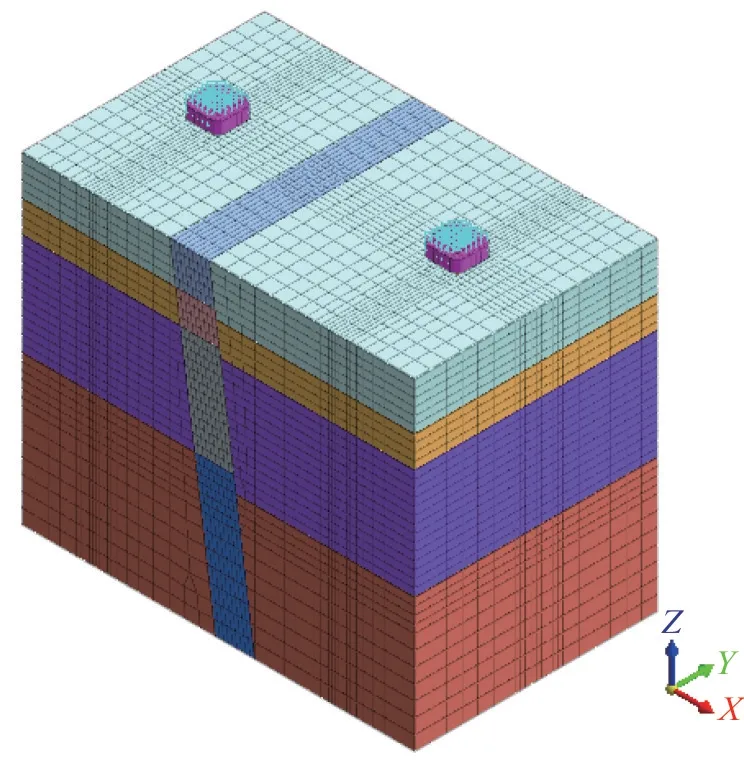
图2 37#和38#墩模型Fig.2 37#and 38#pier model

2.1.2 参数选取

根据海文大桥地勘报告，计算模型中各材料参数见表2。

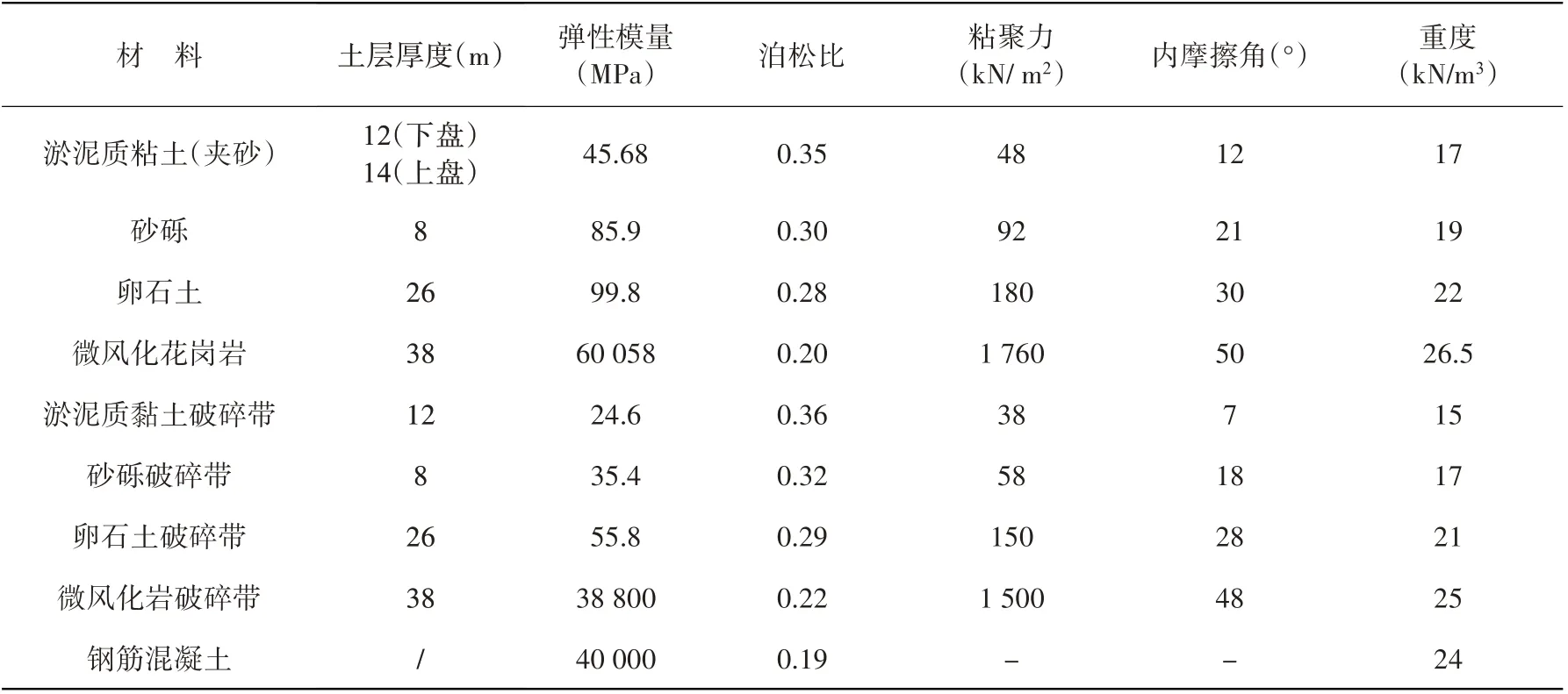
表2 各材料参数表Table 2 Parameters of each material

2.1.3 边界条件

（1）振型分析采用弹性边界

地震振动时程分析第一步先选择地震波，对地震波进行振型分析，从而得到有限元模型的特征周期和阻尼因子，文中利用MIDAS进行数值模拟时振型分析采用弹性边界。

（2）时程分析采用黏弹性人工边界

地震动时程分析时，如果采用静力分析中的载荷与约束施加方案，由于地震波具有反射作用，会导致结果误差较大，大量研究证明黏弹性边界可以提供良好的模拟效果［18-20］，所以文中在时程分析时采用Lysmer提出的黏弹性人工边界［23］。该条件需要在土体外边界添加曲面阻尼弹簧。

2.2 计算方案

2.2.1 地震波选取

选取中国地球物理研究所针对海文大桥人工合成的5010波、5002波以及Kobe波和El-Centro波4种近断层脉冲型地震波时程作为地震动输入，利用基线校正软件SeismoSigal对输入地震波进行滤波和基线校正处理，得到合理的地震波后在保证原有波形不变的情况下，对其加速度峰值按比例缩放，将各地震波峰值限制在0.35 g左右，如图3所示。

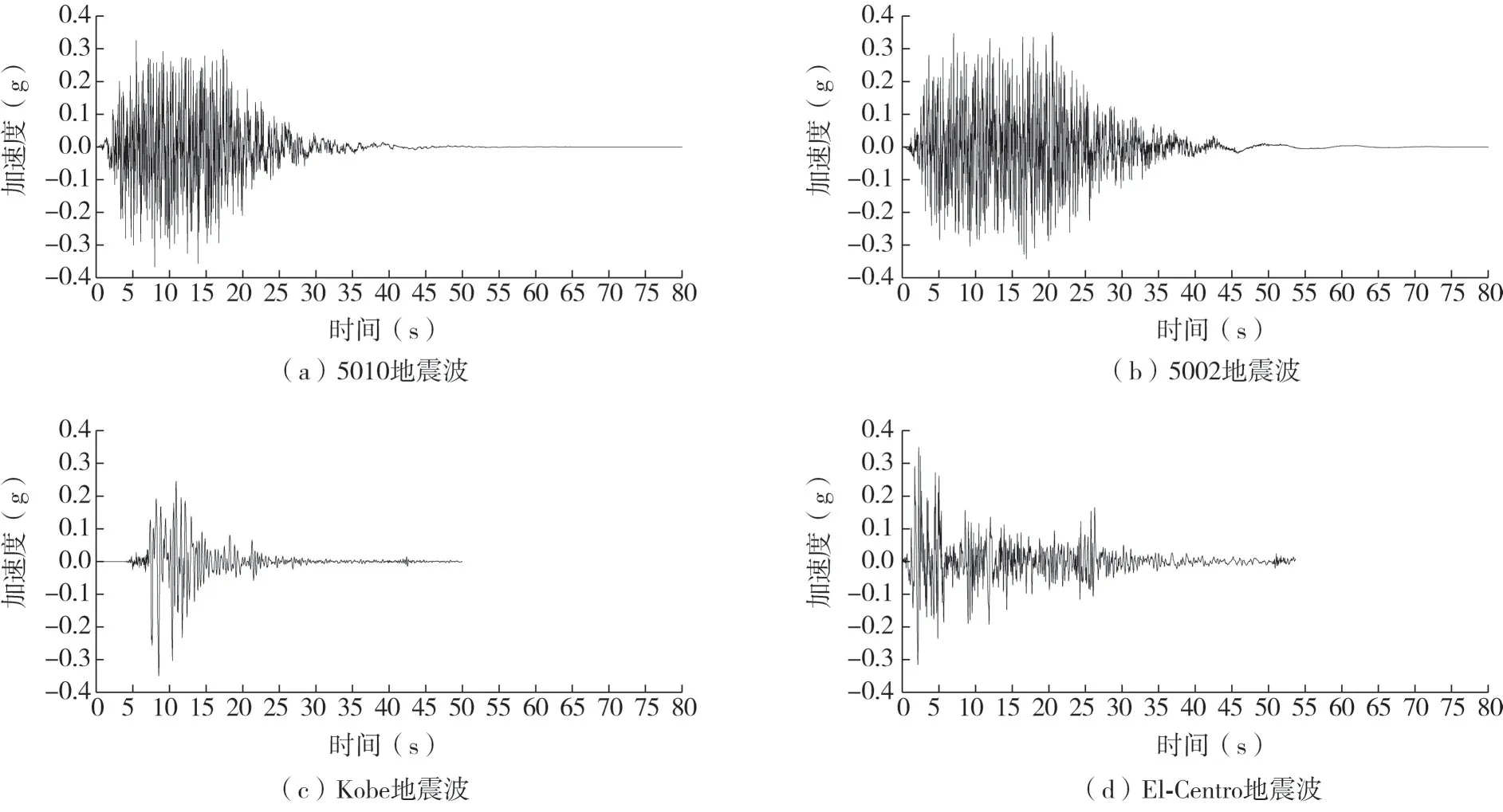
图3 4种不同类型地震波Fig.3 Four different types of seismic waves

2.2.2 工况设计

详细计算工况见表3。桩基避让距离取基岩面近断层一侧桩与断层的水平最小距离。

表3 计算工况Table 3 Calculation conditions

3 不同地震波类型桩基础力学变形特性

3.1 加速度响应

3.1.1 加速度峰值响应

在地震波峰值为0.35 g，不同类型地震波作用下，上、下盘桩基桩身加速度峰值及其放大系数变化规律如图4、图5所示。其中，加速度放大系数α定义为：

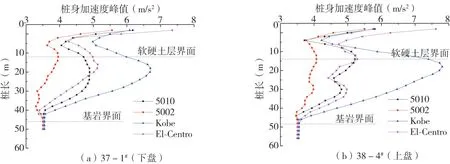
图4 桩身加速度峰值变化规律Fig.4 Variation law of peak acceleration of pile

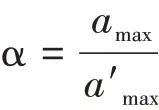
式中：amax为桩身加速度峰值；a′max为输入地震动峰值加速度；α反映岩土层性质及高程对桩身加速度的放大效应。

从图4、图5中可以看出：

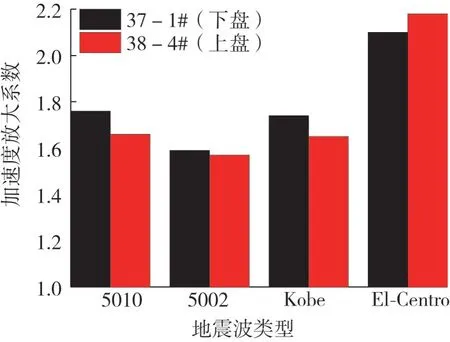
图5 桩顶加速度放大系数Fig.5 Acceleration magnification factor on pile top

（1）不同类型地震波作用下，桩基加速度峰值变化规律相似，均在桩顶与土层分界面较大。桩顶加速度在El-Centro波作用时达到最大，在软硬土层分界面，加速度峰值在Kobe波作用时最大，桩底加速度峰值与输入加速度峰值基本相同，桩底到基岩面处桩身加速度峰值基本没有发生放大或缩小，说明基岩对加速度的影响较小。同一类型地震波作用下，上下盘桩基桩身加速度变化规律有所差异，上盘的桩身峰值加速度大于下盘，产生显著“上盘效应”。

（2）覆盖层土体对桩身加速度具有一定的放大作用（α＞1）。其中，El-Centro波作用下桩身加速度放大幅度最大，放大系数为2.18。5010、5002和Kobe波较小。说明相同土层对不同地震波加速度放大效果并不完全相同，且桩基所处地质条件不同对地震波作用下桩身加速度变化规律影响显著。由于断层的存在，导致上、下盘桩的桩顶加速度放大系数不同（放大系数差值在0～0.86范围内）。

3.1.2 加速度时程响应

由于输入地震动50 s后加速度基本为零，故选取桩基加速度时程响应0～50 s范围进行分析，4种地震波作用下，桩基0～50 s加速度时程响应如图6、图7所示。

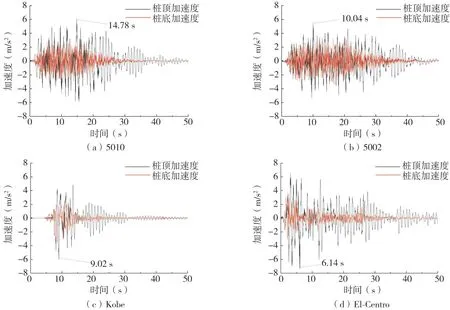
图6 37-1#（下盘）桩基加速度时程Fig.6 Acceleration time history of 37-1#（lower plates）pile foundation

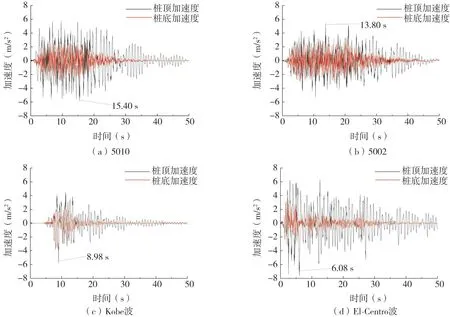
图7 38-4#（上盘）桩基加速度时程Fig.7 Acceleration time history of 38-4#（upper plates）pile foundation

从图6、图7中可以看出：

（1）桩底加速度时程响应的频率和振幅与输入地震波接近，而桩顶时程响应频率较低、振幅较大，以上盘桩基在5010波地震动输入情况下为例，桩顶和桩底加速度分别在50、25 s后趋于稳定，桩顶和桩底加速度峰值分别为5.80 m/s2和3.54 m/s2。其原因是基岩对地震波的响应速率快，对其几乎没有影响，而覆盖层对地震波的“滤波”作用较为明显，将地震波中的高频成分进行了一定的消除，使得桩土惯性相互作用下桩顶对地震波高频成分的响应程度及敏感度降低。

（2）同一类型地震波作用下，断层上、下盘桩基的桩顶、桩底加速度时程响应波形规律类似，由于断层的存在，上盘桩基桩顶峰值加速度滞后于下盘，其中，Kobe波和El-Centro波作用下，上、下盘桩基桩顶加速度峰值出现时刻接近，5010地震波作用下，上、下盘桩基桩顶加速度峰值出现时刻分别为15.40、14.78 s，5002地震波作用下，上、下盘桩基桩顶加速度峰值出现时刻分别为13.80、10.04 s。

3.2 桩顶水平位移响应

断层上、下盘桩基的桩顶水平位移时程响应如图8所示，桩顶水平位移峰值变化规律如图9所示。

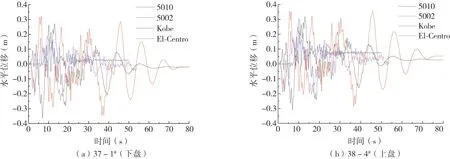
图8 桩顶水平位移时程响应Fig.8 Time-history response of horizontal displacement of pile top

从图8、图9中可以看出：

（1）桩基础达到水平位移峰值时刻与输入地震波类型有关，以下盘37-1#桩基为例，4种地震波作用下，分别在6.96、10.14、11.76、15.96 s时刻达到振幅最大值。

（2）同一类型地震波作用下，上、下盘桩基的桩顶水平位移时程响应规律相似，由于断层的存在使上下盘桩基两侧土层性质有所不同，导致产生永久位移大小不同。在四种地震波作用下，上盘桩基产生永久位移分别为0.03、0.05、0.08、0.01 m，下盘为-0.02、-0.02、0.03、-0.03 m。断层上盘桩基产生的永久位移明显大于下盘，产生显著的“上盘效应”。

（3）桩顶水平位移峰值在不同类型地震波作用下相差较大，以上盘38-4#桩基为例，5010波作用下桩顶水平位移峰值最大，El-Centro波作用下最小，二者相差0.18 m。

3.3 桩身弯矩响应

4种类型地震波作用下，桩身弯矩响应规律如图10所示。根据海文大桥37#、38#墩桩基配筋情况，通过规范计算得到桩基抗弯承载力为37.14 MN·m，桩身弯矩峰值变化规律如图11所示。

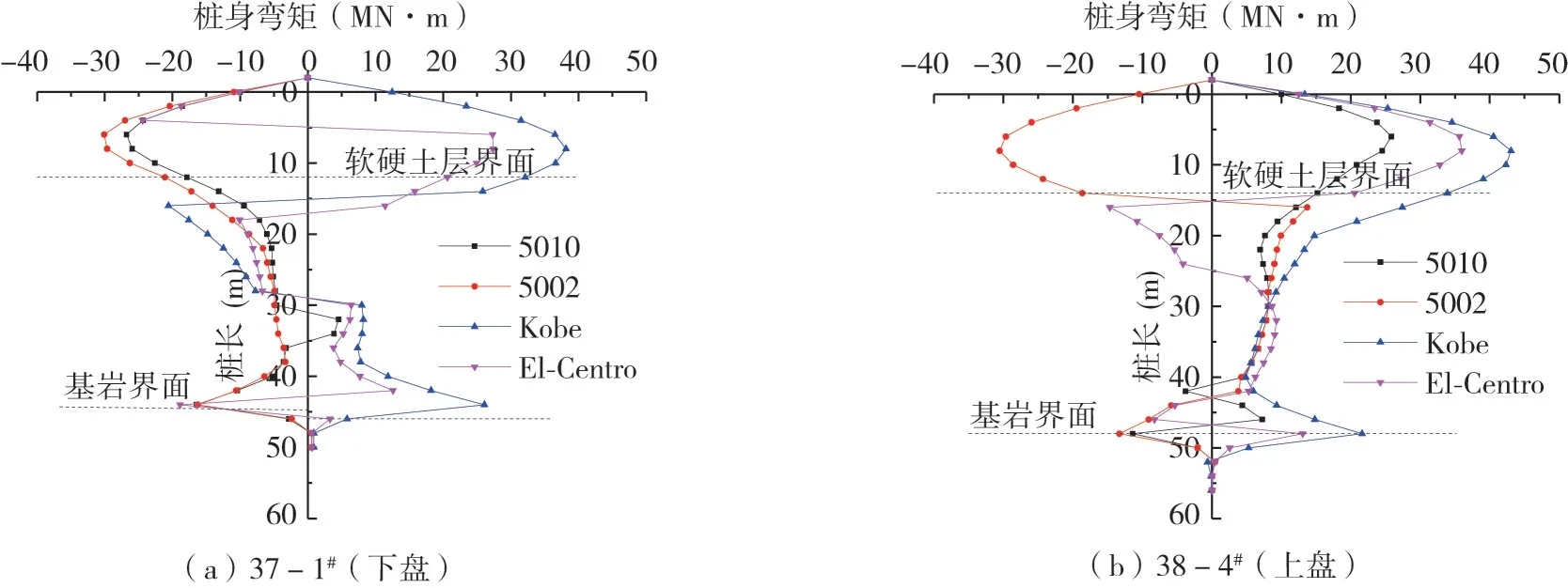
图10 桩身弯矩响应规律Fig.10 Response law of bending moment of pile

从图10、图11中可以看出：

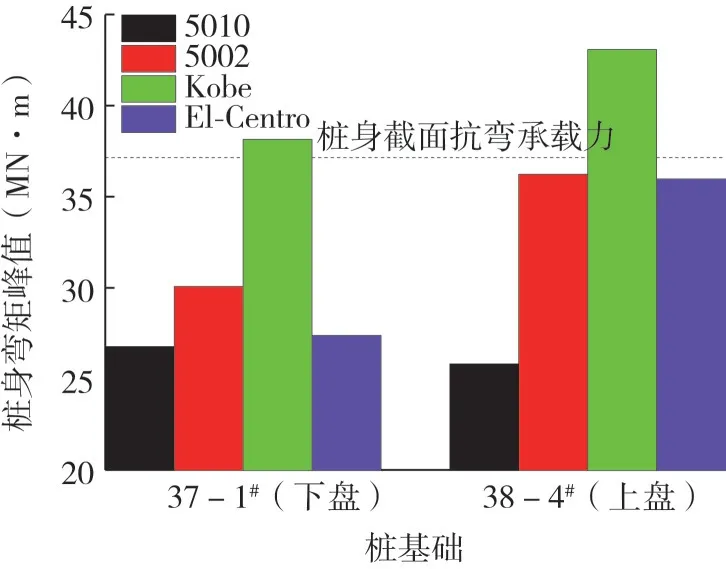
图11 桩身弯矩峰值Fig.11 Peak bending moment of the pile

（1）沿桩长方向上、下盘桩基弯矩变化规律基本相同，均是先增大后减小。并且上、下盘桩基弯矩均在土层分界面及基岩面处出现峰值，原因是此处为岩土体交界面，岩土体的软硬程度变化较大，导致桩身产生较大弯矩。

（2）不同类型地震波作用下，上、下盘桩基弯矩峰值各不相同。5010、5002、El-Centro波作用下，桩基弯矩峰值均未超过桩身界面抗弯承载力，海文大桥设计50年超越概率10%地震动峰值加速度0.35 g，因此，上、下盘桩基抗弯设计均满足要求；Kobe波作用下，下盘桩基弯矩峰值超出桩身截面抗弯承载力2.1%，上盘桩基弯矩峰值超出桩身截面抗弯承载力17.1%。在桥梁桩基础抗震设计时，应重点考虑Kobe波作用对桩基的影响，确保桩基础具有足够的抗震能力。（3）同一类型地震动作用下，上盘桩基弯矩峰值普遍大于下盘，原因是断层、桩周土体差异以及嵌岩深度不同的存在导致“上盘效应”显著。

3.4 桩身剪力响应

不同类型地震动作用下，桩身剪力沿桩长方向的响应规律如图12所示，桩身峰值剪力变化趋势图如图13所示。根据海文大桥37#和38#墩桩基配筋情况，通过规范计算得到桩身截面抗剪承载力为11.3 MN。

图12 桩身剪力变化规律Fig.12 The peak value of the bending moment of the pile body

从图12、图13中可以看出：

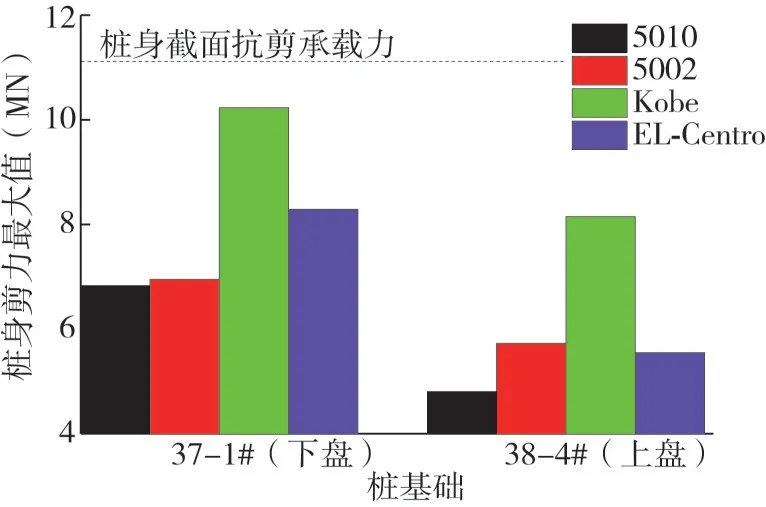
图13 桩身剪力峰值变化趋势图Fig.13 Trend of the bending moment of the pile body

（1）不同类型地震波作用下，在桩身同一截面处桩身剪力随着地震波类型的变化而有所差异。桩身剪力均在桩顶和基岩面附近处较大，且在基岩面附近桩身剪力达到峰值。原因是桩顶承台与上部结构质量较大，在地震动作用下，承台与上部结构产生较大惯性力，导致桩顶与承台连接处产生较大剪力，在基岩与覆盖层的交界处，岩土体的软硬程度差异较大，导致桩身产生巨大剪力。

（2）不同类型地震波作用下，桩身剪力最大值变化较大，其中Kobe波作用时，桩身剪力峰值最大，5010波作用时，桩身剪力峰值最小，二者相差3.34 MN（上盘）、3.4 MN（下盘），与桩身弯矩变化规律吻合。

（3）4种地震波作用下，上下盘桩基础桩身最大剪力均未超过桩身截面抗剪承载力。说明上、下盘桩基抗剪设计均满足50年超越概率10%动峰值加速度0.35 g要求，海文大桥抗震设计安全。

4 结论

（1）覆盖层土体对桩身加速度具有放大作用，并且覆盖层对地震波的“滤波”作用较为明显。桩顶加速度响应滞后于桩底，上盘桩顶峰值加速度响应相对于下盘具有滞后性。

（2）由于断层两侧桩周土体以及嵌岩深度的差异，上盘桩基桩身峰值加速度、产生的永久位移、桩身弯矩峰值均大于下盘，产生显著的“上盘效应”。

（3）断层上、下盘桩基弯矩均在上部土层界面处达到峰值，剪力均在基岩面处达到峰值。

（4）桩顶加速度及其放大系数在El-Centro波作用时较大；在5010波作用时，桩顶水平位移峰值较大；在Kobe波作用时，桩身弯矩、剪力峰值以及桩顶永久位移较大，且最大弯矩超出桩身截面抗弯承载力。

同时，根据数值分析结果提出以下抗震设计建议：

（1）在近断层桩基抗震设计时建议着重考虑上盘桩基础的抗震设计，且考虑上下盘之间桩基础的变形差异引起的上部结构反应。

（2）在进行桩基础抗弯承载能力设计时建议着重考虑软硬土层分界处尤其是土层与基岩交界面附近的桩基抗弯设计。

（3）在进行抗震验算时建议根据不同情况选择合理的地震波波形，其中考虑桩基峰值加速度响应时可以参考对其影响最大的El-Centro波，考虑桩基相对位移响应和桩基弯矩响应时可以参考敏感性最强的Kobe波。