物理地震危险性分析中的地震动模拟方法研究进展

李 奇，陈学良，高孟潭，李宗超

（中国地震局地球物理研究所，北京 100081）

引言

地震灾害是全世界都要面临的严峻问题，严重威胁人民的生命财产安全。破坏性地震在全世界范围内都曾发生过，如1906 年的旧金山大地震、1923 年的关东地震、1976 年的唐山地震、1999 年的台湾集集地震、2008年的汶川地震和2016年的熊本地震［1－9］等，这些地震给全世界造成了重大生命财产损失。尽管工程建筑水平以及抗震措施相对于以前已经有了很大的改善，但是破坏性地震依然会给国家带来严重的损失。

因此，防震减灾工作任重道远。造成地震灾害的原因除了抗震措施不足外，主要是人们缺乏对地震的清楚认知，未能够正确设防，即使在地震研究充分的地区，仍然没能很好地解决。虽然地震难以精确预测，但能通过历史地震以及地质构造特点来推断区域未来可能发生的地震动特点和最大震级，这种方法称为地震危险性分析。地震危险性分析是评定某一区域内工程在有效使用期内遭受一定地震动强度的危险性，分析结果并以设防烈度和设计地震动表示，为工程抗震设计、震害预防和城市规划提供地震动输入［10－11］。由此可见：地震危险性分析是城市规划和抗震设防的重要手段，能够为抗震御灾提供科学的依据。在面对城市遭受过破坏性地震的惨痛背景下，我国极为重视并在21世纪初全面开始和研究大城市的活动断裂探测和地震危险性评价，为我国的经济发展和社会稳定打下了坚实的基础。

由于地震波传播过程中存在非常复杂的随机性和不确定性，但又必须了解和研究地震动的特点，因此地震工程学家需要深入研究地震动特点来为建筑物等结构提供结构抗震设计分析［12－18］。通过地震观测数据来研究地震动特点是常用方法，但在实际分析应用上仍然存在一定的局限性，而随着数值模拟发展越发成熟以及计算条件越发优越，数值模拟已成为研究地震动重要方法之一。地震动数值模拟应用广泛，可用于抗震设计、强地震动基本参数标定、建筑物震害分析、地震动参数输入以及地震危险性分析等［19－22］，本文主要叙述地震动数值模拟在地震危险性分析中的应用。

目前，工程地震大多使用的是经验校准的地震动预测方程来量化未来地震的震动强度，并将得到的地震动作为工程的地震动输入［23－24］。经验方法虽然成熟，但是在没有观测记录的情况下，经验方法是有局限性的，如深沉积盆地的影响［25－26］，而地震动数值模拟是有可以突破这些限制。SCEC/CME就利用地震动数值模拟来预测未来可能发生的地震动［27－30］。这种基于物理实际和真实速度结构的地震动数值模拟［31－32］，能够很好的反应地层速度结构、断层的几何真实异质性和盆地效应等影响［25，33－36］，虽然处在发展完善阶段，但其已经发挥了重要作用，在没有很好观测条件的情况下，能够很好地校正经验方法并得到相对更加合理的结果。不过这种方法同样也面临着重大挑战，如最大截至频率为1Hz、如何将研究区域扩大和如何设置凹凸提参数等。南加州地震中心（SCEC）的CyberShake 项目利用真实断层构建的震源模型和地区三维速度结构模拟了未来地震动并绘制地震危险性曲线，相对于传统地震动预测方程，CyberShake能够更好地模拟出方向性效应和反应盆地效应等波的传播特征，能够为特定场点提供更加可靠的设防依据。

随着计算科学和地震科学的进一步发展，大量的地震数据处理和地震动模拟不再像以前那样困难。除了美国的CyberShake 项目，还有日本的Recipe 方法等，都在尝试用基于物理的地震动数值模拟的方法来计算地震危险性。目前来看：基于地震动数值模拟的地震危险性分析虽然存在不足，但是不能忽略其在未来的发展潜力。本文综述了前人的研究成果，举例介绍了正在进行的研究，探讨未来该方法的研究趋势。

1 地震危险性评价方法

地震危险性问题是对研究区域的在未来可能发生的地震引发的地震动评估，这种地震动危险性分析目前最常用的有两种方法：一是概率性方法是以概率的方式分析、评价与表述未来地震危险性；二是确定性方法由给定的距离和震级下的设定地震引起的地震强度。确定性方法包括历史地震法和地震构造法，取结果之大者作为地震动危险性确定性分析的结果。

1.1 概率性地震危险性分析方法

早在20 世纪60 年代，CORNELL［23］就提出了概率性地震危险性评价方法（PSHA）和潜在震源的概念，并且分点源、线源和面源探讨了其他地震危险性的计算方法。自从CORNELL 提出PSHA 以来，就在世界范围内得到了广泛应用，包括地震区划图的绘制、抗震设计规范的应用和核电设施的安全性评价等。20 世纪70年代，美国绘制了基于PSHA的全国性地震动区划图。随着概率性地震危险性不断发展和完善，不同学者也做了相关研究。KIUREGHIAN 等［37］提出了大地震的破裂长度对计算的危险性有显著影响；REITER［38］把PSHA 大致分为四个环节：（1）划分潜在震源区；（2）确定潜在震源区地震活动性参数；（3）估计地震影响；（4）计算场地的地震危险性，通过这四个环节来计算地震危险性。

PSHA 引入中国后，高孟潭［39］对PSHA 进一步研究并改进已让其符合中国国情—CPSHA，基于该方法编制了“中国地震烈度区划图（1990）”。但是概率性地震危险性分析方法存在诸多的不确定性等问题［40－49］，如何更好地完善PSHA是学者们不断研究和探究的重点。

1.2 确定性地震危险性方法

确定性地震危险性方法（DSHA）分为两类：历史地震法和地震构造法。历史地震法是基于历史资料和调查资料选取最大地震动。地震构造法是基于区域内大地震的构造条件，评估区域内最大潜在地震。由于DSHA 是基于地震科学基础，因此在实际地震危险性分析中也得到了广泛应用。美国在编制新一代的地震区划图时用确定分析的结果修正PSHA 结果。因此基于DSHA 的危险分析方法在抗震御灾上发挥着重要作用。WANG等［50］用DSHA绘制台湾地区的地震动危害图，发现50年超越概率10%的平均PGA（峰值加速度）和PSHA 计算结果基本一致；ZUCCOLO 等［51］将DSHA 和PSHA 预测结果和真实地震活动做了对比，发现DSHA 预测结果更加贴近真实记录；MUALCHIN［52］和MURMAN 等［53］建议在地震设计中使用DSHA。所以即使在PSHA占据主要评定方法的情况下，DSHA的作用也不能忽视。

2 地震动数值模拟

丰富的地震记录能够在研究地震时起到关键作用，但是对于地震记录稍显不足或稀缺的地区（包括地震活动性处在相对较弱时期的地震带），越发成熟的数值模拟是弥补这些区域地震危险性研究的必要方法。目前地震动数值模拟方法主要分为：确定性方法、随机性方法和混合方法。

2.1 确定性方法

确定性方法是在基于AKI等［54］的弹性动力学表示定理，将地震动表达为震源函数与格林函数的时空卷积。目前确定性方法主要包括，有限元方法、有限差分法、离散波数法和谱元法等［55－66］。众多的学者用确定性方法研究了断层的盆地效应和滑冲效应、速度大脉冲等地震动特征［67－73］。

对于长周期地震动（＜1Hz），确定性方法能够很好的模拟，然而对于短周期分量，确定性方法表现较差，这是因为在短周期地震动包含较强的随机性，地壳模型和破裂过程中存在不均匀性，因此单一固定的震源时间函数不能反映随机性和不均匀性。

2.2 随机性方法

随机性方法是基于高斯带限白噪声的随机振动理论方法［74－75］，或者是基于小震的经验格林函数方法［76－78］，该方法适用于短周期（频率一般大于1Hz）地震动。前者在小震和远距离观测的情况下考虑为点源模型［79］，在大震和近距离时考虑为有限断层模型［80－81］。经验格林函数法是将研究区域符合要求的（主震震源机制和信噪比高的小震记录等）地震记录作为经验格林函数模拟地震动［82－83］，经验格林函数法已经包含了场地效应和路径效应等信息，因此不用再计算复杂的理论格林函数。经验格林函数的不足之处是难以模拟小震记录匮乏的地区。

2.3 混合方法

混合方法是将确定性方法和随机性方法结合起来利用各自的优势，在高频段采用随机性方法，在低频段用确定性方法，在分别模拟后经过适当的高通和低通滤波之后，在时域中叠加合成宽频带的强地震动［84－88］。虽然混合方法利用了确定性方法和随机性方法的优点，但是混合方法也存在一定的局限性［89］，比如确定性信号结束与随机信号开始的衔接处容易产生反应谱的畸变，而这段频率往往是工程上关注的频段范围，因此混合方法还需要不断地优化。

3 地震动数值模拟在物理地震危险性分析的应用

3.1 CyberShake项目

OWENS［90］提出将计算科学和地震科学结合起来之后，南加州地震中心（SCEC）的CME（Community Modeling Environment）项目颇受关注［29］。CME 项目旨在系统地研究地震科学，其重要目标就是研究区域地震危险性并为未来工程建设和震害防御提供科学依据。初期项目开展后，SCEC 分为两个研究团队。前者开发基于Java程序的算法—OpenSHA［91］。OpenSHA 能实现多种地震危险性概念计算包括ERF（地震预测模型）、IMR（烈度度量关系）和IMT（烈度度量类型），OpenSHA 能为CME 提供了更加灵活的建模环境，让其在复杂计算需求下仍能适用。后者构建南加州的三维速度模型（CVM-V3.0）［92－93］，其能反应真实地层的起伏并为地震动数值模拟提供更高的计算精度。模拟地震动与观测记录的对比表明精细的三维速度结构能更好地模拟地震动的传播。

烈度度量关系（IMRs）和地震破裂预测模型（ERFs）是计算PSHA 的两个关键。ERF 是在给定确定场点条件下，能够生成该区域可能发生的地震集合。此外，还能给出每一个地震的震级和发生概率等。这些地震的集合是根据历史地震、断层活动性和断层尺度等来确定的。IMR 是地震波随距离的衰减关系。起初，IMR 使用的是经验衰减关系，后来基于波形的IMR 发展起来（即后来的CyberShake 项目），SCEC 科学家们希望CyberShake能够取代传统的衰减关系来推测未来南加州地区的地震危险性。

近年来，SCEC/CME 还开展了多项研究。面向工程的地震动模拟宽频带平台（Broadband Plantform）［94－98］，基于物理的全概率地震危险性分析项目——CyberShake［99－100］，高频带扩展项目（High-F）［101］，基于三维层析成像技术的三维速度结构模型（F3DT）等［31，102］。其中：CyberShake将确定性震源和波传播效应纳入地震动模拟中，由此来计算地震危险性，计算流程见表1。为了更好地构建南加州地震实验场的地震危险概率分析的精度和提高模拟的频率上限，CyberShake 也在不断的发展和完善，如ERF 的更新换代和构建更加精细的CVM等。

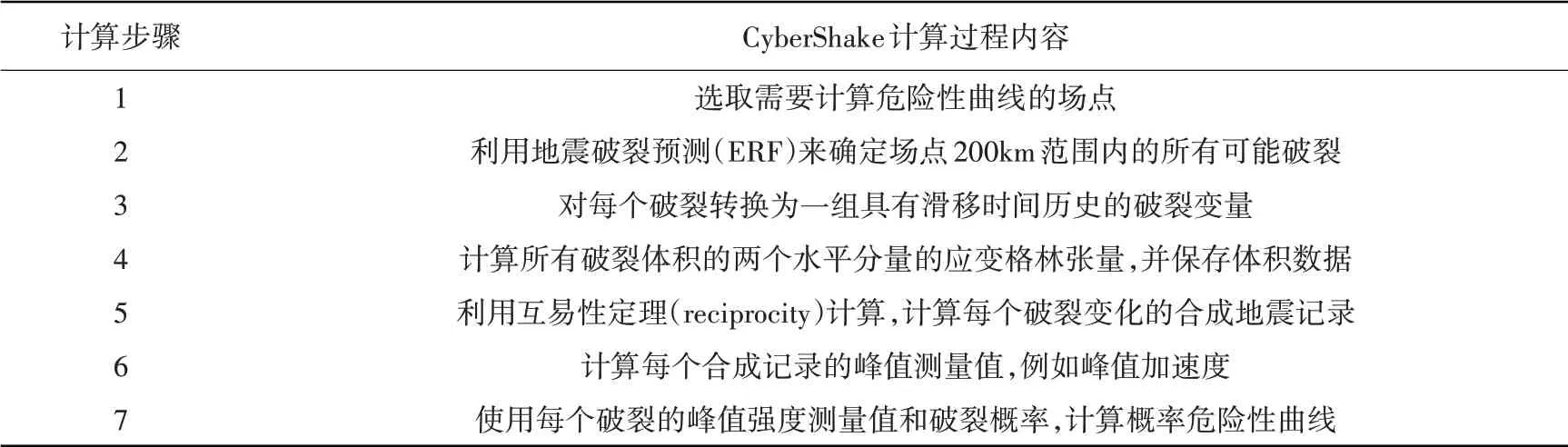
表1 CyberShake的计算流程［99］Table 1 The workflows of CyberShake

CyberShake 计算地震危险性时，采用的是确定性震源，大量的计算不可避免，计算范围内的地震震级越大，产生的破裂变化也越多，因此计算会消耗大量的计算内存和时间。为了能够降低计算成本，利用互易定理（reciprocity）产生大量的格林应变张量（SGT）来合成地震图从而节约计算成本［34，103－104］。虽然利用互易定理降低了计算成本，但是互易定理的计算要求是弹性介质［105－107］，难以反应非弹性非线性的性质。为了能将非弹性的性质考虑进地震动模拟中，将近断层的非弹性性质纳入到破裂模型的震源效应里，将近地表的非弹性性质纳入到路径效应里，这样即能保证其弹性介质要求又能考虑非弹性影响。SCEC 还采用了一种新的范式（paradigm）来取代传统震源效应、路径效应和场地效应的解耦计算［108－109］，在新的范式下，地震动模拟可以计算非线性响应，并且震源、路径和场地效应是耦合计算的，通过新的paradigm 能够更加恰当地体现断层外的非弹性性质和浅表地层的流变性质。

不过，CyberShake 项目仍然具有局限性：①波动场的计算模型是伪动力学（运动学）震源模型，并非真正意义上的动力学模型；②相对于工程感兴趣的频段（1～10 Hz），项目计算的最大截止频率为1 Hz；③弹性计算条件限制，无法实现真正意义上的非弹性计算条件。这些都是需要面对的巨大难题，相信随着认识的增加和计算效率的提升，CyberShake会不断地完善和发展有望在未来地震危险性分析中扮演重要角色［110－115］。

确定性震源的地震动模拟方法能够模拟出盆地效应和速度大脉冲等特征，能反应特定地质构造下的地震动特征，这是衰减关系难以做得到，但是CyberShake 目前还处在发展阶段存在限制和不足如：地层速度结构不够精细和断层系统的理解局限等，未来会随着计算能力的加强和认识探索的不断深入，CyberShake极具潜力。

3.2 Recipe方法

ERC（Earthquake Research Committee）在2005 年出版了两种日本国家地震灾害图［116］：一种是基于PSHA的地震灾害图；另一种则是指定震源断层的地震灾害图。前者是表明全国不同地区可能发生的强烈地震的可能性，而后者想要预测区域内各个地震共同作用下的强地震动，ERC 把这种预测强地震动的方法称为Recipe 方法。Recipe 方法是由IRIKURA［117－118］提出的，其将地震动的长周期和短周期分量分别用有限差分法和随机格林函数法计算，然后借此来预测由活断层引发的强地面运动。Recipe 方法的关键点在于震源模型的建立，IRILURA 把震源参数分为三类：外部震源参数（outer fault parameters）、内部震源参数（inner fault parameters）和额外震源参数（extra fault parameters）。

外部断层参数包含整个断层的几何尺寸和地震矩。参数可由下式计算［119－120］：

式中：M0为地震矩；为平均应力降；S为断层面积；W和L分为是断层的宽度和长度；a和b分别取1.4 ×10-2和1。式（1）适用于地震矩小于1019Nm的情况和式（2）用于大于1019Nm的情况。

内部断层参数有凹凸体参数（包括面积、应力降等）和加速度震源谱幅值（amplitude of acceleration source spectrum level）。内部断层参数表征断层非均质性的特点。参数可由下式计算［121－123］：

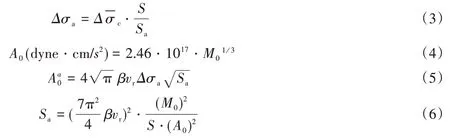
式中：Δσa为凹凸体上的应力降；Sa为凹凸体面积；A0和Aa0分别是加速度震源谱幅值和凹凸体上的加速度震源谱幅值；β和vr分别是介质中的S波传播波速和破裂速度。对于内陆地震SaS取0.22，对于俯冲型地震SaS取0.25。

额外断层参数为破裂起始点和破裂速度。由这两个参数定义破裂传播的规律。对于内陆地震，破裂规律主要和活断层的特征相关［124］，其中俯冲型地震更多是参考历史地震的破裂规律。

Recipe方法预测强地面运动的流程图和震源参数设置步骤分别如图1-2所示。由①②求得特定地震的震源模型；由②③来估计格林函数。利用震源模型和格林函数预测地震动，再由历史地震数据验证模拟地震动的合理性［125－130］。Recipe方法已经在多次历史地震上成功验证［131－132］，并且提出了多尺度空间异性的方法来验证更大型的地震（≥M8.0）［133－134］。对于历史记录缺乏的区域，由于震源模型难以预估，采用不确定性来刻画未知震源参数［135］，随着方法不断修正完善，Recipe 方法适用性会更强。不过Recipe 方法仍然存在缺陷如：凹凸体的数量无法确定，在没有地震记录的地区，震源模型参数如何设置，地层速度结构不够精细等。

图1 震源参数设置步骤Fig.1 The steps of setting source parameters

Recipe 方法利用了丰富的观测资料和地层数据来刻画震源参数，由此来模拟未来可能发生的地震动。Recipe 方法充分利用地震记录丰富的优势，通过大量地震数据反演断层震源信息，在应用到未来可能发生的地震上。但是该方法在地震记录较少的地方应用困难，而且该方法对断层内部参数的设定仍需要完善。

图2 Recipe方法预测地震动流程图Fig.2 The flow chart of ground motion prediction by Recipe method

4 物理地震危险性分析中地震动数值模拟方法的展望

过去地震动的模拟或预测在面对地震观测记录稀少、对地层速度结构的认识有限和计算能力匮乏时，非常难以实现基于物理的地震动模拟和预测。想要实现大范围的多线程的计算从计算上和理论上都是比较困难的。地震动数值模拟在近20 年来，发展极为迅速，不断更新的计算模型和优越的计算条件都为应对复杂问题提供了基础。未来，地震动数值模拟会是研究地震危险性的重要手段，甚至朝向取代经验衰减关系的目标发展。虽然利用数值模拟在计算地震危险性上存在许多的不足与局限，但不否认其发展的潜力，在震害防御、抗震设防和工程结构抗震中都会有广阔的发展前景。基于上述介绍，未来数值模拟在地震危险性分析中的研究及发展趋势有以下几个方面：

（1）将非弹性响应嵌入到对应计算程序中；构建更加精细的三维速度模型；更好地确定震源参数。在弹性介质中，如何将非弹性非线性的地震动波动现象高效和集中地模拟出来，是即将面对的一个难题。此外，还需要对三维速度结构（特别是浅表地层）做更深的探索，比如采用密集节点列阵、光纤传感器或者是激光雷达的方式来完善地层结构模型，通过这些措施增加对断层系统的理解，提高计算频率等。对于基于凹凸体的地震动预测方法，如何更好的确定内在断层参数（凹凸体位置和数量等参数），也是需要面临的重大挑战，这将会是未来研究的一个方向。

（2）与经验衰减关系的博弈。基于数值模拟的地震危险性分析还处在一个研究、探索、验证和完善的过程。那么不可避免地会与经验衰减关系作比较，最近的研究表明数值模拟的方法是可行的。那么到底是用经验关系还是地震动数值模拟的结果作为预测参考？本人认为目前还是以经验关系为主，地震动数值模拟的方式作为修正。因为地震动数值模拟的方式尚处在发展和探索阶段，并且研究区域较小，如若要扩大应用范围、实际应用到工程之中需大量时间和基础工作。因此，在未来，基于地震动数值模拟的地震危险性分析会成为计算地震危险性的常规手段，只不过还需不断地发展、完善和论证。

（3）对我国的启示。我国地处环太平洋地震带与欧亚地震带之间，地震活动十分活跃，同时也是全球地震灾害较为严重的国家。随着西部战略和海洋强国战略的实施，越来越多大型建筑都在山区及复杂地形环境中开展建设，那么抗震设计可能难以适应这些特殊地区的工程设防要求，而地震动数值模拟能够很好地弥补这一缺陷，通过震源模型和速度结构模拟出地震波的传播效应，从而为特殊区域提供地震危险性分析和提供设防依据。因此，地震动数值模拟会是研究区域地震危险性的重要手段之一。

数值模拟在物理地震危险性分析上的发展还远没有结束。作为涉及计算科学和地震科学等多学科、具有重要现实意义和广泛应用的研究领域，研究地震危险性将会成为地震动数值模拟的重要研究方向。