基于EDEM-FLUENT的液力湍流磨内部流场的数值模拟

2022-05-10叶文旭杨小兰刘极峰

南京工程学院学报（自然科学版） 2022年1期

叶文旭,杨小兰,孙凯,陈杨,崔润,刘极峰

(南京工程学院机械工程学院, 江苏南京 211167)

在现代工业中,超细粉体因其特有的性质而占有重要地位.随着社会、科技的发展,以及能源的日益枯竭,粉体的市场有增无减,将来还会需要粒度更小、纯度更高、材质更硬的粉体,所以研究和发展结构更优、效率更高的磨机十分必要.近年来,伴随着湿式磨机的持续发展和研究的不断深入,国外的湿式磨机产品已日趋完善,但是国内湿式磨还存在研磨效率不高、物料细度不够等关键技术瓶颈问题,亟待解决.

国内外专家对磨机进行了一定研究.文献[1]利用FLUENT模拟了不同转速下研磨装置内流场的分布情况;文献[2]通过分析流场速度、湍流强度和剪切率参数,研究磨腔内流场的运动规律;文献[3]依据CFD技术以EM型磨机为研究对象,分析研究磨腔速度场、压力场、温度场、颗粒轨迹等特性.

本文基于EDEM和FLUENT进行耦合仿真,对液力湍流磨进行流场分析,并用数值模拟试验验证其合理性,得到较为准确的分析结果.

1 模拟方法

1.1 模型的建立

在液力湍流磨中,磨介颗粒与流体均在一定的闭合空间内进行运动,且该流体为不可压缩的牛顿流体,对模型进行简化后仿真.液力湍流磨的容积约为780 mL,研磨筒内径D=100 mm,高度H=100 mm,涡轮叶片直径d=90 mm,叶片倾角α=15°.利用SOLIDWORKS三维建模软件对模型进行绘制,其简化模型如图1所示.

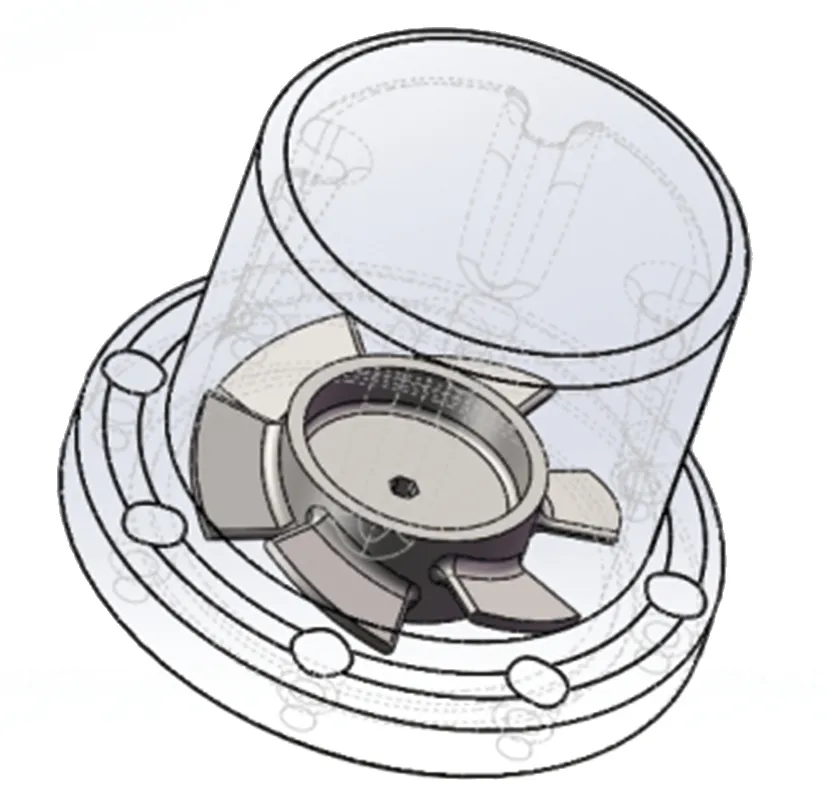
图1 液力湍流磨三维模型

1.2 网格划分

将SOLIDWORKS中建立的三维模型导入至ANSYS中的ICEM,在筒内对涡轮叶片建立一个动域的方案.在预处理中利用布尔操作将三维模型分为转动区域和静止区域.在整个筒内区域中分离出转动区域,再在转动区域中分离出涡轮叶片部分,即完成了布尔操作.对该模型的流体域进行网格划分,最小网格尺寸为0.124 mm,最大网格尺寸为2.307 mm,网格总数为646 302,最小的网格体积为1.200 1×10-13mm3,最大网格体积为1.650 7×10-7mm3,网格的扭曲度小于0.97,在计算精度允许的范围内.网格划分如图2所示.

图2 液力湍流磨网格模型

1.3 EDEM参数设置

EDEM-FLUENT耦合模型属于Euler-Lagrange模型,用Euler法控制流体的连续介质,用Lagrange法控制离散相的磨介颗粒.本文采用0.50、0.75、1.00、1.50 mm粒径的同材质磨介颗粒,按照输入的粒径及密度输出其质量与体积.EDEM软件提供三种不同的粒径分布方式,通过对液力湍流磨的工作工况、磨介材料以及磨介粒径大小的研究分析,本文选用固定粒径分布方式,且四种粒径的磨介颗粒以4∶3∶2∶1的球配比进行混合填充.为简化计算,设定磨介颗粒为球形.磨介颗粒表面几乎无黏附力,磨介颗粒与磨介颗粒、磨介颗粒与筒壁间的碰撞均采用Hertz-Mindin模型进行模拟,并设置重力加速度方向.本文在EDEM中设定的具体参数如表1所示.

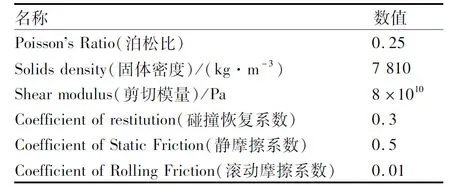
表1 磨介颗粒材料参数

在液力湍流磨的研磨过程中,磨介颗粒由颗粒工厂生成并沉降至筒内.在筒底上方75 mm处设置长50 mm、宽50 mm的四边形颗粒工厂,考虑到磨介颗粒的生成速度受软件计算能力限制,设置颗粒工厂随机产生磨介颗粒速度为2 000粒/s,颗粒按1 m/s的下降速度沉降至筒底.待沉降完成后通过Simulation Deck在当前时间点导出,并将Set Simulation Time设置为0 s做为耦合的起始点.磨介颗粒在发生接触碰撞过程中,瑞利波消耗的能量占总能耗的26%,在EDEM中将时间步长设为2×10-10s.打开EDEM中的Start Coupling Serve接口,将EDEM设为待接收耦合信号状态,等待与FLUENT建立连接.

1.4 FLUENT参数设置

调用FLUENT中的Read指令读取Journal耦合文件.在ICEM中将网格模型设置完成后导入至FLUENT中,对该网格进行Make Polyhedra多面体处理,使网格在FLUENT中更加易于计算,并通过Check指令做网格质量检测.本文将对冲湍流磨的仿真工作简化为液-固两相流瞬态数值模拟.在研磨模拟时采用滑移网格模型解决对冲湍流磨磨腔内动、静区域的结合,其中动、静区域的交界面设置为数据交换面interface,动、静区域的数据交换面完成.涡轮叶片设定为动壁面边界条件,对冲湍流磨筒内壁设定为壁面边界条件,应用Euler-Euler模型进行固-液两相流的耦合,在Euler坐标系下求解瞬态雷诺平均N-S方程及标准k-ε湍流模型.在Lagrange坐标系下求解各个磨介颗粒的运动方程.固-液两相之间的耦合由颗粒曳力和两相动量交换的迭代计算完成.

2 控制方程分析

2.1 流体控制方程

流体质量守恒方程为[4]：

(1)

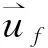
流体动量守恒方程为：

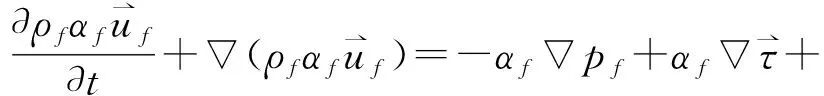
Sf+αfρfg

(2)

单相流与两相流的区别在于αf与Sf的差别：

(3)

(4)

2.2 磨介颗粒受力分析

2.2.1 颗粒与流体作用力分析

磨介颗粒位于流体之中,随流体一同运动,由于对冲湍流磨筒内流场特性颇为复杂,使磨介颗粒受多种作用力,其合力为：

Ff=Fd+Fp+Fvm+Fsaff+Fml+Fb

(5)

式中：Ff为磨介颗粒所受流体的合力;Fd为磨介颗粒所受流体的阻力;Fp为压力梯度力;Fvm为虚拟质量力[7];Fsaff为萨夫曼升力[8];Fml为马格纳斯力[9];Fb为倍瑟特力[10].

由于本文中磨介颗粒较小,因此忽略Fsaff、Fml、Fp、Fvm、Fb对磨介颗粒的影响[11],Fd在其各个作用力下起主要作用[12].在磨介颗粒的运动速度高于流体流动速度的情况下,磨介颗粒所受流体的作用力变为阻力,反之为曳力[13]：

(6)

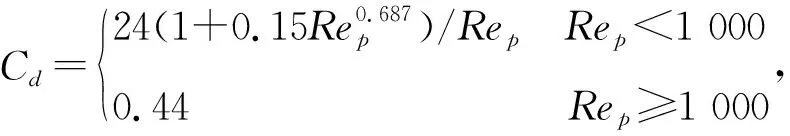
2.2.2 颗粒动力学方程

取磨介颗粒群中的第i个磨介颗粒为研究对象,此颗粒运动分为平移运动与旋转运动,由牛顿第二定律可知[14]：

(7)

2.3 颗粒碰撞模型

对颗粒群中颗粒碰撞过程进行假设：磨介颗粒均为球状刚体;颗粒群中只存在任意两个颗粒的碰撞;磨介颗粒密度相同,直径不同,且初始状态分布均匀.

磨介颗粒群中任意两个颗粒碰撞后均满足动量定理,如图3所示[15].

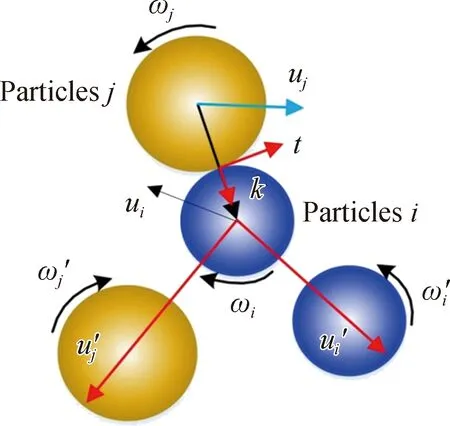
图3 磨介颗粒碰撞示意图

颗粒碰撞模型为：

(8)

3 数值模拟结果与分析

3.1 磨介颗粒分布统计

为了直观分析磨介颗粒在筒内的分散规律,使用EDEM软件中的Setup Selection功能建立Grid Bin Group,将筒体划分成12个分析区域,如图4所示.

图4 筒内区域划分

为分析磨介颗粒在筒内流场的运动状况,选取A、B、C、D、E、F六个等体积区域,分析各区域内的颗粒数目变化情况.磨介颗粒数目随时间变化的情况如图5所示.

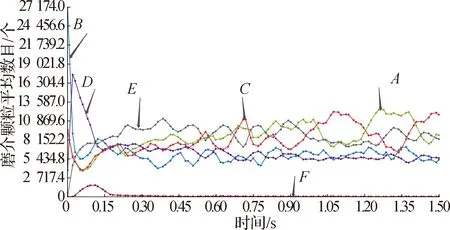
图5 不同区域磨介颗粒数目随时间的变化

由图5可以看出,在初始时刻,颗粒工厂磨介颗粒产生速度为2 000粒/s，以1 m/s的速度下落.A、B、C、D区域的初始值相对较高，在0.10 s时出现转折点,而后运动相对平稳.在磨介颗粒的整个运动过程中,颗粒群主要分散在涡轮叶片附近,而筒内顶部的流场中颗粒较少.由于重力加速度的原因,大量磨介颗粒沉降于A、B、C、D四个区域,B区域磨介颗粒量最多为27 174.0个,D区域内的磨介颗粒量最少为4 076.1个.由图5可见,E、F区域的磨介颗粒分布折线的起始点均为0.

A、C区域靠近涡轮叶片端部,磨介颗粒主要在该区域发生分散.对比A、C区域可知,在0.50 s后,两区域的磨介颗粒数目发生互补现象,说明A、C区域间的颗粒发生交替运动,该区域内的颗粒数目反映涡轮叶片的运动产生涡流并带动颗粒周向运动的现象.

B区域为涡轮叶片的中心位置,通过颗粒工厂生成的大量磨介颗粒沉降在此区域,所以该区域起始点较高.在涡轮叶片高速转动后,将此区域的磨介颗粒排向筒内各个区域,在0.05 s时磨介颗粒数目急剧下降,而后逐渐平稳.

D区域为涡轮叶片的正上方,涡轮叶片运动后,A、C区域处的颗粒运动至D区域,在0.05 s时磨介颗粒数目激增,而后逐渐降低并趋于平稳.

E区域为涡轮叶片的右上方,由于磨介颗粒密度较小,沿径向排出的磨介颗粒受到筒壁的阻挡时,大部分颗粒反弹至该区域,且筒内中心位置有涡流的产生,使得磨介颗粒在涡轮叶片正上方的数目比两侧少.

F区域为筒壁顶部,在初始时刻,涡轮叶片高速运动,部分磨介颗粒通过与壁面碰撞进入该区域,在0.10 s左右达到最大值,而后受旋转涡流的影响,该区域内的磨介颗粒数目几乎为0,即F区域为湍流磨的死区,在仿真过程中该区域几乎没有磨介颗粒.

3.2 单个磨介颗粒运动轨迹

通过EDEM软件可以提取单个颗粒随时间变化的运动轨迹,如图6所示.由图6(a)可见,颗粒工厂生成的磨介颗粒下落后,经过涡轮叶片运动,随着自由液面涡流向下移动,在碰撞涡轮叶片后,受冲击作用沿径向排出,在受到筒壁阻碍后弹出,向上运动至液面,并被液体卷吸,进入循环流动;由图6(b)可见,颗粒工厂生成的磨介颗粒下落至筒底,涡轮叶片产生的涡流带动其向上运动,被涡轮叶片径向弹出后与筒壁碰撞,开始沿涡轮转动方向运动,并在涡流的带动下逐渐向上运动,进行下一轮循环流动.

(a) 粒径0.75 mm颗粒

3.3 筒内流速矢量图分布

通过EDEM和FLUENT耦合仿真,在FLUENT中可获得筒内流速的分布情况,使用Plane Tool功能截取涡轮叶片上方平面,通过Counters获取该平面处的流速矢量图,如图7所示.在流速矢量图中,最大速度为3.37×10-4m/s,最小速度为3.43×10-8m/s,最大速度与最小速度量级相差104,筒内产生巨大的流速差,该现象表明,筒内涡流进行了有效的扩散形成了有利湍流场由于流速差的原因,涡轮叶片在运动过程中给低流速区域颗粒增加颗粒动能,对颗粒的能量进行输入,大大增加了颗粒的碰撞次数.

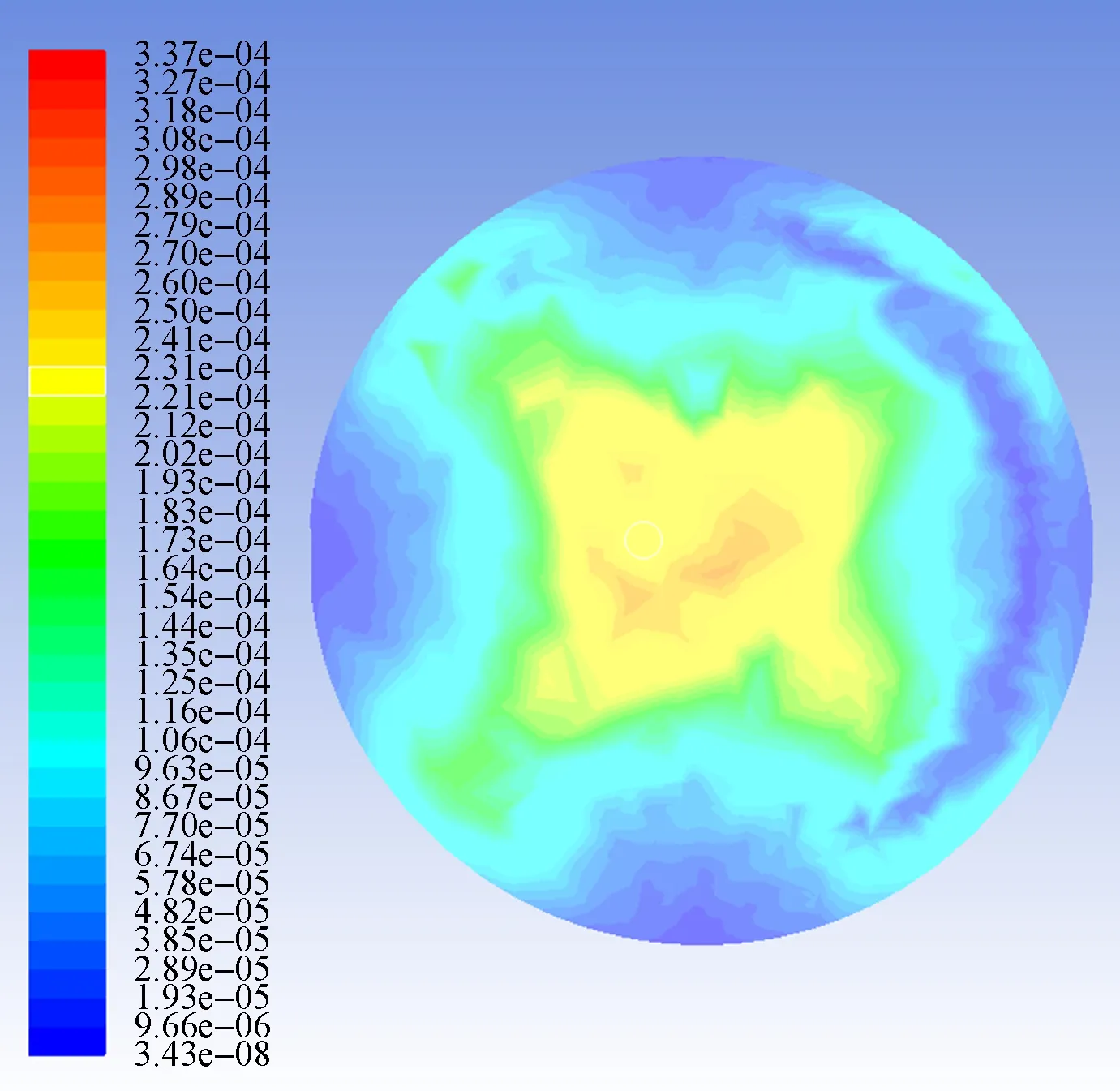
(a) 筒内横截面

图7(a)为筒内横截面的流速矢量图,筒内流速主要分布在3.43×10-8～1.16×10-4m/s,占比在60%以上,筒内流场分布相对均匀,按照圆周状分布,分布规律为由内向外逐渐降低，即随着涡轮叶片的转动在筒内中心处形成涡流,该区域产生较大的速度.图7(b)为筒内立截面的流速矢量图,可知筒内中心速度最大,靠近筒壁的速度相对较低,在筒内产生了明显的涡流现象,并且越靠近中心位置流速越大.根据以上规律可知,涡轮叶片的转动能产生较强的旋转涡流,能使磨介颗粒获得更大的动能.

由图7可知,F区域的速度矢量较最中心位置略低,即流体在到达F区域后流速有所降低,由于重力加速度的原因,颗粒也会自由下落至涡轮叶片中心位置.流速矢量图的分析与磨介颗粒分布统计分析相符,在筒顶的F区域内颗粒极少,因此在实际工况中,应适当增加涡轮叶片的转速,从而带动流体产生更高的转速,有助于中心位置流速的扩散.由图7(b)可知,在筒体内壁的流速矢量图中,侧壁的速度明显低于筒体顶部的速度,筒内流场整体呈中心向四周减弱,筒体顶部相对于侧壁处于中心位置,因此在实际工况中,应加强筒体顶部的防磨损措施来应对该现象.

3.4 离散颗粒速度分布

离散颗粒的速度反映了颗粒的动能,即所获得能量的大小.颗粒在磨腔中随时处于与其他颗粒、磨腔的碰撞中,动能也是随时发生变化的,在EDEM中对颗粒速度分布进行分析,如图8所示.

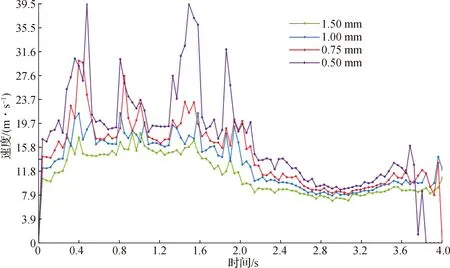
图8 磨介颗粒平均速度随时间变化图

由图8分析可知,四种粒径磨介平均速度的大体趋势与整体相似,但也稍有不同.其中0.5 mm粒径磨介最高平均速度为39.5 m/s,0.75 mm粒径磨介最高平均速度为30.1 m/s,1.0 mm粒径磨介最高平均速度为21.4 m/s,1.5 mm粒径磨介最高平均速度为18.17 m/s.粒径小的磨介平均速度较高,但碰撞后整体速度丢失快,随着时间变化,只有少量颗粒保持速度,这表明,在湍流场中,小颗粒自身速度快,但容易因碰撞丢失动能;粒径大的磨介最大平均速度低于小粒径颗粒,但保持时间长,这表明,大粒径磨介初始时刻获得动能时间长,但一旦获得动能,就会拥有较高的速度及冲击力,碰撞发生后不会很快丢失动能,进而往复.

3.5 流场湍动能的分布规律

湍流运动是立式涡轮磨机磨筒内流场最为明显的能级特征,截取XZ平面上的湍动能,如图9所示.分析得可知,湍动能较大的区域大部分集中在涡轮叶片周围,最大湍动能为9.392×102m2/s2,磨筒内其他流体域的湍动能则没有这么明显.图9中涡轮叶片上方筒壁处存在两处高湍动能区域，该区域为磨筒内部与扰流筋的交界面，湍动能的能级达到7.632×102m2/s2，且形成了湍流漩涡.