函数空间上的一类算子方程的解

赵国俊

(南京工程学院数理学院, 江苏 南京 211167)

设H为希尔伯特空间,其上的有界线性算子的全体记为B(H)(构成Banach代数). 对于给定的算子A、B、C∈B(H),考虑算子方程(Sylvester方程):

AX-XB=C

(1)

其中满足方程的未知算子X称为该算子方程的解.

算子方程(1)通常称为Sylvester-Rosenblum方程,它起源于矩阵方程及微分方程的相关研究. 自20世纪50年代取得了突破性进展之后,该方程受到了广泛而深入的研究[1-4].另一方面,经典的函数空间如Lebesgue空间、Hardy空间以及这些空间上的有界线性算子如乘法算子、Toeplitz算子等也得到了许多学者的关注[5-7].

本文将算子方程与函数空间上的特殊算子两者相结合,研究由函数空间L2(T)上的乘法算子以及Hardy空间H2(T)上的Toeplitz算子所构成的算子方程的解,借助于算子谱的性质刻画了方程存在唯一解的充分条件. 在探究Toeplitz算子的性质基础上,得到了唯一解相关的充要条件,并给出了唯一解的具体形式.

1 预备知识

复平面C上的开单位圆盘记为D,单位圆周记为T=∂D.L2(T)为关于T上规范化测度μ的Lebesgue空间. 设H(D)为D上解析函数的全体,此范数下,其子集H2=H2(T)为Hilbert空间(或记为H2(D)),内积定义为:

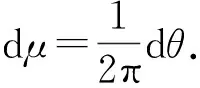
设φ∈L∞(T),L2(T)上的乘法算子定义为Mφf=φf,∀f∈L2(T).H2(T)上的Toeplitz算子定义为Tφf=P(φf),∀f∈H2(T).这里P为L2(T)到H2(T)的投影算子,函数φ一般称为相应算子的符号.

引理1[5]：

1)σ(Mφ)=R(φ),这里σ(·)表示算子的谱,R(·)表示函数的本性值域；

引理2[6]：

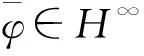
B(H)上的左乘算子LA与右乘算子RB分别定义为(对于任意的X∈B(H))LA(X)=AX,RB(X)=XB.广义导数(算子)ΔA,B=LA-RB,即ΔA,B(X)=AX-XB.算子方程(1)可表示为ΔA,B(X)=C.

引理3[2,4]:σ(ΔA,B)=σ(A)-σ(B)={λ-μ:λ∈σ(A),μ∈σ(B)}.

2 主要结果及证明

引理4：设H=L2(T)且φ、ψ∈L∞(T).若R(φ)∩R(ψ)=∅,则B(H)上的算子方程MφX-XMψ=C有唯一解.

证明：方程即ΔMφ,Mψ(X)=C. 由引理1知,σ(Mφ)=R(φ). 据引理3有σ(ΔMφ,Mψ)=σ(Mφ)-σ(Mψ)=R(φ)-R(ψ). 由于R(φ)∩R(ψ)=∅,知0∉R(φ)-R(ψ),故0∉σ(ΔMφ,Mψ),从而ΔMφ,Mψ可逆. 因此,方程MφX-XMψ=C有唯一解.

注记1：利用文献[4]中关于谱刻画更精细的定理,结合乘法算子的谱的特点,可以进一步证明：R(φ)∩R(ψ)=∅⟺方程MφX-XMψ=C有(唯一)解.

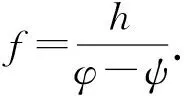
证明：

1) 必要性,若X=Mf为原方程的解,利用乘法算子的交换性,可知C=MφMf-MfMψ=M(φ-ψ)f为乘法算子;

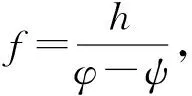
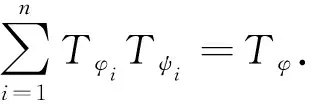
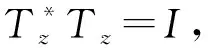
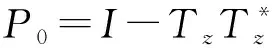
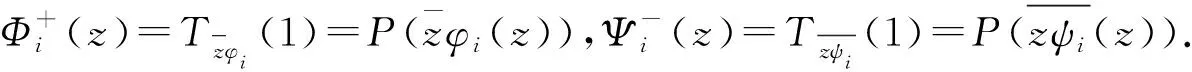
注意到z、ω的任意性,可知结论成立.

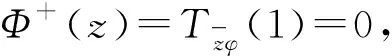
显然，当n=1时,即引理2的2).

引理5：设φ1、φ2、ψ1、ψ2∈L∞(T),则Tφ1Tψ1+Tφ2Tψ2=Th的充要条件是φ1、φ2、ψ1、ψ2满足下列任一条件：

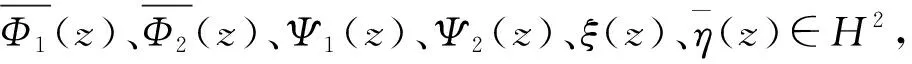
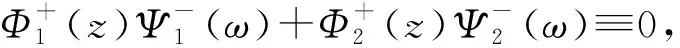
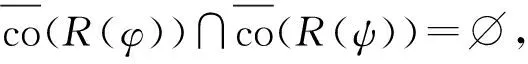
定理3：在引理6的条件下,当C=Th是Toeplitz算子时,方程的唯一解X也是Toeplitz算子的充要条件为符号h具有形式：h=(φ-ψ)g,g∈L∞(T),并且下列3个条件中至少1条成立：

1)g=c为常数；

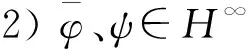
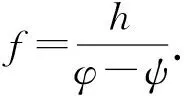
证明：

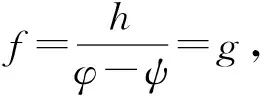
①g=c.当g=c(常数)时,取f=g=c,则TφTf-TfTψ=Tcφ-Tcψ=Tc(φ-ψ)=Th.

③g具有形式g=r(Φ++Ψ-)+a0,为了讨论方便,记Φ+=P(φ)-φ(0),Φ-=(I-P)(φ)+φ(0),Ψ+=P(ψ),Ψ-=(I-P)(ψ).显然φ=Φ-+Φ+,ψ=Ψ-+Ψ+. 取f=g,故

TφTf-TfTψ=TφTg-TgTψ=

TφTr(Φ++Ψ-)+a0-Tr(Φ++Ψ-)+a0Tψ=

(TφTr(Φ++Ψ-)+TφTa0)-(Tr(Φ++Ψ-)Tψ+Ta0Tψ)=

(TφTr(Φ++Ψ-)-Tr(Φ++Ψ-)Tψ)+T(φ-ψ)a0=

(TφTrΦ++TφTrΨ-)-(TrΦ+Tψ+TrΨ-Tψ)+T(φ-ψ)a0=

TφTrΨ--TrΦ+Tψ+TrφΦ+-TrΨ-ψ+T(φ-ψ)a0=

TΦ-+Φ+TrΨ--TrΦ+TΨ-+Ψ++TrφΦ+-TrΨ-ψ+T(φ-ψ)a0=

(TΦ-+TΦ+)TrΨ--TrΦ+(TΨ-+TΨ+)+TrφΦ+-

TrΨ-ψ+T(φ-ψ)a0=

TΦ+TrΨ--TrΦ+TΨ-+TΦ-rΨ--TrΦ+Ψ++TrφΦ+-

TrΨ-ψ+T(φ-ψ)a0=

rTΦ+TΨ--rTΦ+TΨ-+TΦ-rΨ--rΦ+Ψ++rφΦ+-rΨ-ψ+(φ-ψ)a0=

TΦ-rΨ--rΦ+Ψ++rφΦ+-rΨ-ψ+(φ-ψ)a0=

T(r(Φ++Ψ-)+a0)(φ-ψ)=Tg(φ-ψ)=Th

故结论成立.

2) 必要性,若X=Tf为方程的解,即TφTf-TfTψ=Th,变形得TφTf+TfT-ψ=Th.由引理5可知,φ1=φ,ψ1=f,φ2=f,ψ2=(-ψ)满足引理中的条件.

由引理5条件1),直接验证可得定理3中的条件1)与条件2)(四种情形).

由引理5条件2)的结论,注意到φ=Φ-+Φ+,ψ=Ψ-+Ψ+,代入可得方程组：

化简得:

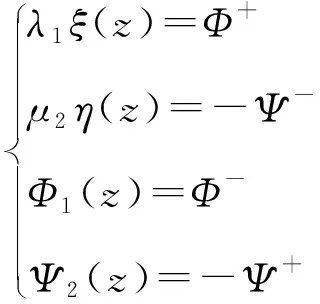
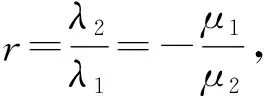
故结论成立.

注记3:注意定理3条件3)中,当Φ+=0或者Ψ-=0时并不能包含前面两种情形,此时仅仅是条件1)与条件2)的一部分特例.