基于主成分分析-线性回归的光伏发电功率预测研究
2022-05-10陈黎来李世纪吕高宇吴巧鑫曾艾东
杨 婷,陈黎来,李世纪,吕高宇,吴巧鑫,曾艾东
(南京工程学院电力工程学院, 江苏 南京 211167)
据统计,截至2020年12月底,我国光伏并网装机共2.53×108kW.2021年全国风电、光伏发电量占全国用电量的11%左右[1].光伏出力具有分散性、间歇性、随机性与波动性的典型特征,随着光伏渗透率的不断提高,给电网电能质量和设备安全带来严重影响,同时将使得电网对光伏出力的调度、管理难度进一步增大.因此,针对光伏发电功率开展精确预测,可以促进光伏与电网友好互动,提高电网对光伏柔性调度能力,提升消纳清洁能源的效率,助力我国实现“碳达峰”和“碳中和”目标[2].
光伏发电是典型多变量耦合随机过程,建立光伏发电功率模型的方法可分为物理建模、统计建模以及混合建模[3].文献[4]建立了气溶胶光学厚度物理模型,能够对辐照强度实现预测.但建模过程若仅考虑辐照强度,将遗漏许多关键气象因子,导致预测模型准确性受到严重影响[5-6].统计建模通过对历史数据进行统计分析,找出其内在规律实现预测.基于统计理论运用机器学习算法建立遗传算法[7]、神经网络[8-10]、支持向量机[11]、日前算法[12]以及极限学习机[13]等预测模型,该类模型本质上为黑箱模型,存在物理机理不清晰的缺陷,模型的精确性高度依赖训练样本数据量,算法复杂程度较高,不利于工程实现,适用于短期、超短期预测.混合建模综合物理建模与统计建模两种方法,通过历史数据进行统计分析,找出其内在蕴含规律构建物理模型.文献[14-15]采用混合建模方法建立光伏发电功率预测的线性回归模型,相比经典物理模型预测精度显著提高,与统计建模相比具有明确的物理机理,且其技术路线易工程化,适用性更佳.由于现有模型构建过程中历史数据所包含的气象因子种类有限,导致预测模型KMO(Kaiser-Meyer-Olkin)检验结果较差[15],提取的主成分会丢失较多的特征信息,严重降低了模型的有效性.
考虑光伏发电功率受到多种气象因子的影响,在模型构建过程中准确提取气象因子特征量将进一步提高功率预测精度.针对上述问题,基于数据驱动思想,本文提出一种主成分分析与逐步线性回归相结合的光伏发电功率预测混合建模方法.
1 主成分分析-线性回归建模
1.1 基于相关性分析的自变量预选
设光伏发电功率Ph为因变量,将光伏发电功率历史样本数据进行归一化处理后,采用Pearson相关性系数作为相关性分析指标对多维气象因子自变量进行预选,其表达式为:
(1)

Pearson系数直观反映因变量与自变量相关性强弱,通常|r|>0.4认为有明显的相关性.筛选出与因变量存在较强相关性的自变量后,进一步检验变量之间的相关性是否显著.构造基于t分布的显著性检验统计量为:
(2)
式中,n为单个气象因子样本数量.
由t分布中得到显著性指标sig,当sig<0.05时,认为X与Y显著线性相关.
1.2 逐步线性回归建模
对p个气象因子自变量X1、X2、X3、…、Xp建立光伏发电功率预测模型:
(3)
式中:β为回归系数,由最小二乘法计算得出.
采用逐步线性回归建模时,逐步引入自变量,每引入一个自变量后都要对其进行F检验,并对已经入选的自变量逐个进行t检验.当旧的自变量由于新引入的自变量变得不再显著时,将其删除.F检验的构造统计量为:
(4)
在F分布表中查表得到对应的sig,当sig<0.05时,认为模型显著.
1.3 模型多重检验
1.3.1 拟合程度检验
R2是功率预测模型拟合程度的决定系数,表示自变量对因变量的解释程度,R2越接近1表示拟合程度越好,计算式为:
(5)

由于R2随着功率预测模型中自变量个数的增加而增大,为了防止R2虚假增大,引入调整系数:
(6)
1.3.2 有效性检验
通过德宾沃森系数DW检验模型是否存在自相关性,公式为:
(7)
式中,Ut为误差项.
当DW趋近于2时,表明自相关性造成的影响可以被忽略.若模型存在较强的自相关性,会使最小二乘法拟合出的β系数不具备有效性,甚至导致模型预测功能失效.
1.3.3 多重共线性检验
方差膨胀系数VIF用于检验功率预测模型是否存在多重共线性,同时检验当前模型所包含的自变量是否冗余,公式为:
(8)
式中,ri为第i个自变量对剩余自变量作相关分析的负相关系数.
当VIF>5时,表明当前模型存在严重共线性,需要进一步修正.
1.4 基于主成分分析的模型修正
若模型未通过有效性或多重共线性检验,需采用主成分分析对已预选的气象因子自变量进行解耦和降维重构,将多个自变量转换为少数的主成分变量.
1.4.1 适用性分析
对待提取主成分的多个气象因子自变量做KMO和巴特利特(Bartlett)球形检验.检验统计量KMO是用于比较自变量间简单相关系数和偏相关系数的指标,表达式为:
(9)
式中:p为自变量个数;rij为变量i和j的Pearson系数.
当KMO>0.65时,表明所选择的气象因子自变量适合提取主成分.Bartlett球形检验用于检验自变量是否各自独立,由相关系数矩阵的行列式计算得到Bartlett球形检验分布.如果该分布的sig<0.05,认为自变量间存在相关性,适合做主成分分析.
1.4.2 主成分提取步骤
1) 对初始模型所包含的气象因子自变量历史样本数据X做标准化处理,处理后的数据记为X′;
2) 构造数据矩阵V进行特征分解,求取特征值λi和对应的特征向量ωi,降序排列特征值λi;
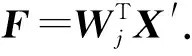
2 模型构建
基于主成分分析-线性回归的光伏发电功率预测模型的构建流程如图1所示.
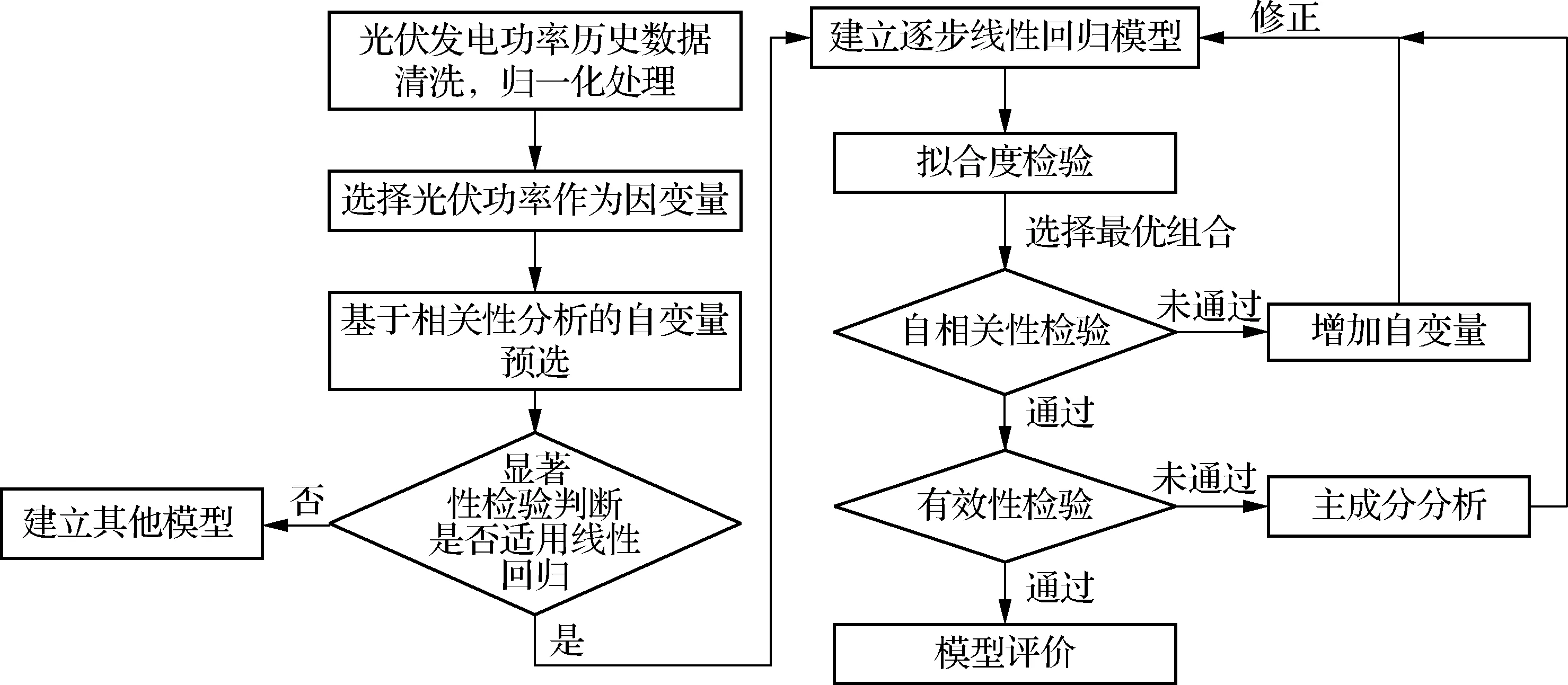
图1 光伏发电功率预测模型流程图
历史样本数据与训练数据均源自澳大利亚爱丽丝泉微型光伏发电单元[16],额定功率为10.5 kW,数据采集周期为每5 min一组.经过基本数据清洗,去除夜间数据和无效数据后样本数据总数约为44 000组.设因变量为光伏发电功率Ph(W),潜在的自变量为样本数据中所有的气象因子,包括总水平辐射强度G、阵列辐射强度P、法向辐射强度D、风向WD、风速WS、垂直风速WV、温度T、湿度H.
2.1 自变量预选
考虑到云层运动将会对太阳辐照产生影响,且云层运动与风速有较强的关系,在无法直接获得云层运动信息的情况下,采用与风速相关的信息代替云层运动信息.通过对比分析多种对风速信息经过数学变换后的新因子与光伏发电功率的相关性,得出对风速取对数后的数据与光伏发电功率的相关性最高,且二者有显著关系,因此将其定义为LNWS,选取其作为预选变量.采用Pearson系数与t分布统计量对样本数据进行相关性分析与检验,结果如表1所示.

表1 相关性分析结果
表1的9种气象因子与发电功率均有显著性关系.其中:G、P、D均与发电功率呈现极强的正相关关系;T、H、LNWS与光伏发电功率呈现较强的正相关或负相关关系;WS、WD、WV与发电功率的相关性较弱.依据相关性分析结果,预选出|r|>0.4的G、P、D、T、LNWS、H6个气象因子作为初始模型的自变量.依据t分布统计量得到的显著性指标sig,认为G、P、D、T、LNWS、H6个气象因子与光伏功率显著线性相关.
2.2 初始模型建立
将6个气象因子自变量对发电功率因变量做逐步线性回归建模,并对模型进行拟合程度与有效性检验,结果如表2所示.

表2 逐步线性建模检验结果
经过对比分析,包含G、H、D、T、LNWS以及P的模型6,由于其拟合程度与有效性检验结果均优于其他模型,被选为初始模型.通过逐步线性回归建模后得到初始模型所包含自变量的回归系数βi,结果如表3所示.

表3 初始模型拟合系数结果
表4为初始模型多重共线性检验VIF结果,其中变量P与G未通过共线性检验.
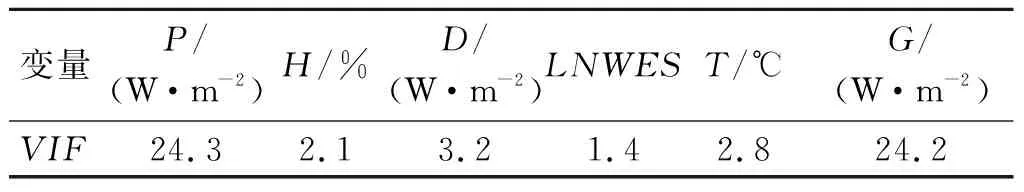
表4 初始模型VIF系数结果
2.3 模型修正
表2所示初始模型6的DW为1.999,表示初始模型无需针对自相关性进行修正.由于初始模型中变量P与G未通过共线性检验,因此采用主成分分析对初始模型进行修正.随机挑选初始模型中的若干个自变量进行KMO检验,选择通过KMO检验且结果最优的自变量组合进行主成分分析.经过分析,G、P与D组合的KMO检验值最优,检验值为0.685;G、P与D合成变量与剩余自变量的Bartlett球形检验为0,表示合成变量与剩余自变量完全独立.
G、P、D在合成变量中的占比系数分别为0.358、0.363、0.334,其数值来源于特征向量矩阵αi,将该合成变量定义为综合辐射强度:
E=0.358G+0.363P+0.334D
(10)
通过主成分累积特征值方差百分比衡量提取出的主成分对于被提取自变量的解释程度,一般取值在85%~95%.表5表明所提取的主成分能够比较全面解释被提取自变量特征.

表5 主成分总方差解释
表6所示为经过修正模型的检验结果,表明修正模型仍然通过了拟合程度与自相关性检验.

表6 修正模型检验结果
修正模型拟合系数和VIF如表7所示,经过修正后的VIF均满足VIF≤5的要求.

表7 修正模型拟合系数与VIF
综合分析表6、表7,修正模型各项系数均满足拟合程度、自相关性检验以及多重共线性检验要求.
3 模型评价
将修正模型与经典模型、未修正模型的预测效果进行对比分析,进一步评价修正模型的正确性、有效性与优劣性.
3.1 残差分析
修正模型拟合结果的散点分布如图2所示.设定标准差超过[-3,3]可认为是异常值.残差分析结果表明,由大约44 000组样本数据得到的拟合结果中存在650组左右的异常值,占比约1.47%.

图2 回归值与残差的散点图
图3和图4分别为标准化残差的P-P回归图与直方图.从图3和图4可以得出,残差满足正态分布,表明了修正模型的合理性.

图3 标准化残差的P-P回归图
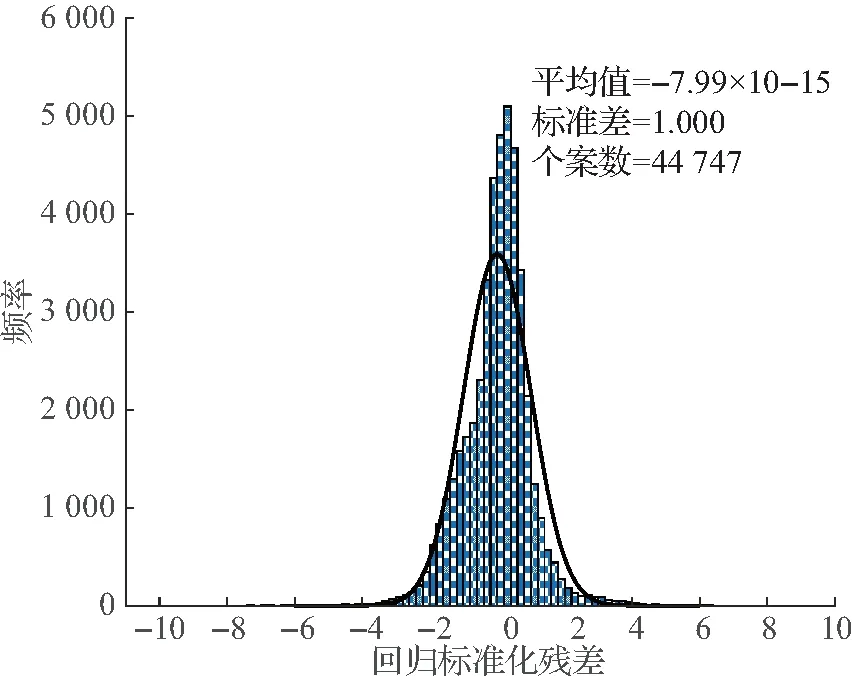
图4 标准化残差直方图
3.2 模型对比分析
为定量分析修正模型预测能力,采用R2、均方根误差(RMSE)、平均绝对误差百分比(MAPE)对预测精度进行评价.随机抽取样本训练数据,通过对不同时间尺度,如单日、单周以及单月的光伏发电功率进行预测,对表8所示的经典模型、未修正模型与修正模型的预测精度进行对比分析.

表8 各模型预测精度
图5所示为不同时间尺度下光伏发电功率预测结果对比.由图5的真实值、经典模型、未修正模型以及修正模型预测结果可见,在不同时间尺度下,修正模型的预测结果准确度明显优于其他模型,更接近真实值.
将修正模型与经典模型、未修正模型的预测精度进行量化,对比分析结果如表9所示.
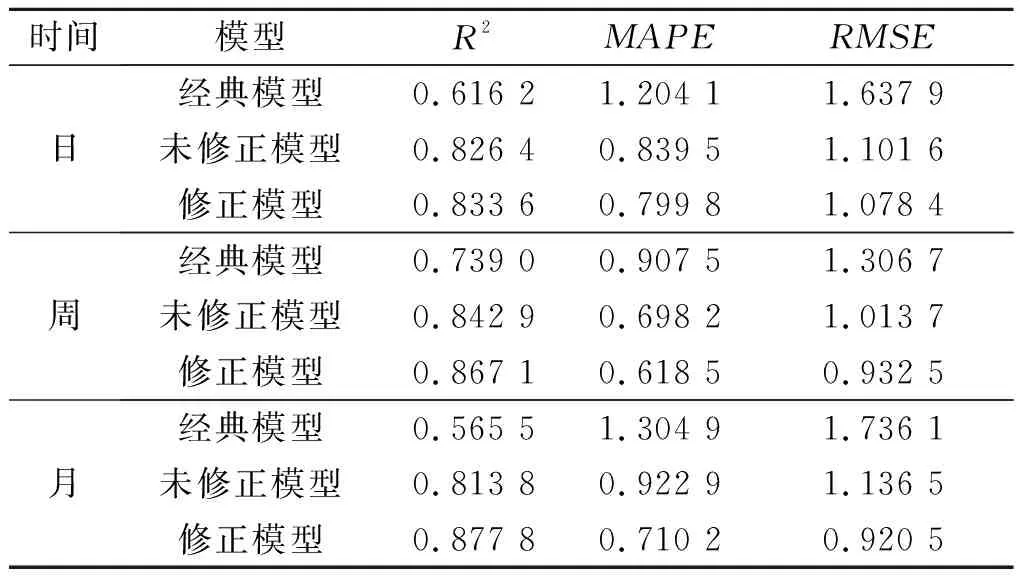
表9 三种模型预测精度对比结果
从对比分析RMSE结果,单日修正模型比经典模型与未修正模型预测精度分别提高了约34.1%、2.1%;单周修正模型比经典模型与未修正模型的预测精度分别提高了约17.3%、2.9%;单月修正模型比经典模型与未修正模型的预测精度分别提高了约47%、19%.
4 结语
提高光伏发电功率的预测精度是增强其可调度性的有效手段.基于数据驱动思想,提出基于主成分分析-线性回归的光伏发电功率预测模型的混合建模方法.首先提出了基于相关性分析的自变量预选、基于逐步线性回归的初始模型构建以及基于主成分分析的模型修正理念;然后合理选取辐射强度、湿度、温度以及风速的对数等多维气象因子自变量,其中综合辐射强度是包含水平总辐射强度、阵列辐射强度以及法向辐射强度等特征信息的合成变量;最后通过对拟合程度、有效性、多重共线性等指标进行综合检验分析,表明了修正模型的合理性.
通过对模型预测能力进行对比分析,得出基于主成分分析-线性回归建立的光伏发电功率预测模型的表现明显优于经典模型,表明了所提混合建模方法的有效性与优越性,且其技术路线具有易于工程实现的特点,对快速建立光伏发电功率预测模型有一定的参考价值.
