典型雷达电磁辐射阻塞效应敏感判据
2022-05-10魏光辉任仕召王琛哲
赵 凯,魏光辉,任仕召, 王琛哲
(1.中国人民解放军63870部队,陕西 华阴 714200;2.陆军工程大学 石家庄校区 电磁环境效应国家重点实验室,河北 石家庄 050003;3.中国人民解放军61969部队,河北 保定 071000)
雷达在现代战争中扮演着“千里眼”的角色,在战场信息获取、构建精确打击武器系统等方面发挥着重要作用.由于交战各方大量使用电子信息装备,战场上电磁信号密集,强度动态交叠,对抗特征突出,电磁环境日趋复杂,对电子信息系统、信息化装备和信息化作战产生严重影响[1].雷达作为用频装备,其战技性能的正常发挥强烈依赖于战场电磁环境,研究雷达装备电磁辐射效应规律是提升其电磁防护性能的基础工作,具有重大的军事应用价值.
电磁敏感度通常用来表示受试设备在电磁信号作用下产生的不希望的响应或降级的量度[2].电磁敏感判据是电磁敏感度研究的基础,与一般意义上的干扰效果评估存在差异.干扰效果评估侧重于装备的技术性能,在此方面已有大量成果报道,国家也制定了相应的军标[3-6].而在武器装备电磁辐射效应预测的背景下,笔者研究的电磁敏感判据旨在最大程度地降低验模误差、提高重复性,保证后续研究的顺利进行.前期已针对无线电引信、通信电台等用频装备的电磁辐射效应预测进行了研究,其思路是从效应机理出发,对复杂电磁环境下武器装备电磁辐射效应进行建模,而后基于恰当的敏感判据对电磁辐射效应规律及临界干扰特性等进行试验研究[7-13].由此可见,合适的敏感判据是进行上述试验研究的基础,对于有关雷达的研究而言,结合理论与试验确定电磁辐射效应敏感判据,为科学预测雷达在复杂电磁环境中的受扰状态提供依据.
本文中,笔者在分析雷达阻塞干扰机理的基础上,以某型X波段脉冲雷达为受试设备,开展了雷达电磁辐射阻塞效应试验,将有效干扰概率作为阻塞效应敏感参数并对其规律进行研究,进一步给出了相应的敏感判据及其测试误差.
1 雷达电磁辐射阻塞效应机理分析
阻塞效应属于电磁辐射场作用之一,是指当强干扰信号与有用信号同时加入射频前端时,接收机增益下降、灵敏度降低,甚至无法接收.下面以单频正弦波为干扰信号进行分析.选择单频正弦波的原因在于,根据傅里叶级数的原理,任何满足狄里赫利条件的信号都可以分解为直流和许多三角函数的分量,正弦波是组成复杂电磁环境的基本信号,将其作为干扰信号更易于分析效应规律,以实现研究目的.
假设空间电磁波进入接收机的信号为
ur(t)=AsEscosωst+AjEjcosωjt,
(1)
其中:ωs与ωj分别为有用信号与单频干扰信号的角频率;Es与Ej为空间中有用信号与干扰信号的场强;As与Aj为有用信号与干扰信号场路耦合及到达非线性电路前的选择系数.
非线性电路的输入输出关系常用精确至三阶的幂级数来表示[10],即
(2)
其中ai(i=0,1,2,3)为非线性系数,与电路特性有关.
将(1)作为输入信号代入(2),得到输出有用信号基波分量
(3)
故有用信号增益为
(4)
干扰信号强度较小时,系统工作在线性区,有用信号增益K≈a1;随着干扰信号增强,非线性失真不可忽略,出现增益压缩现象,有用信号输出电平减小直至0,非线性系数a3<0.
2 雷达电磁辐射阻塞效应试验
由上述电磁辐射阻塞效应机理分析可以推测,若用单频正弦波信号对雷达进行辐照,随着信号强度增大,接收机输出的有用信号电平逐渐降低,雷达对目标的检测能力下降,目标依照回波由弱到强依次消失.据此设计试验,观察雷达在干扰下产生的具体现象,选择合适的雷达电磁辐射阻塞效应敏感参数.
2.1 试验配置
受试雷达为某型X波段脉冲雷达,具有测量目标距离与方位角的功能.其工作带宽为±40 MHz,测距范围为15~15 000 m,方位扫描角为0 °~360 °,采用波导缝隙阵天线,极化方向为水平极化.图1所示为受试雷达主机界面与收发天线.

图1 雷达主机界面与收发天线Fig.1 Radar Host Interface and Transceiver Antenna
试验的具体布置如图2所示.干扰端由信号发生器、频谱分析仪、辐射天线、定向耦合器组成.试验中,信号发生器将干扰信号通过定向耦合器注入辐射天线,频谱分析仪监测干扰功率.辐射天线指向受试雷达,且与雷达天线、测试目标成三点一线.为保证试验结果的准确性,试验在开阔场地进行,场强不均匀性小于3 dB[14].
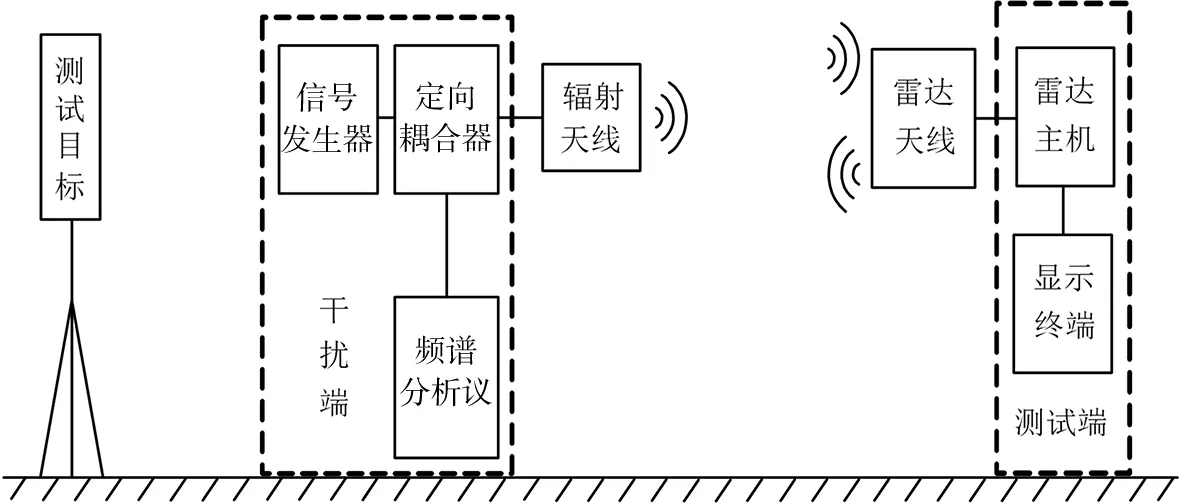
图2 试验配置图Fig.2 Test Configuration Diagram
2.2 电磁辐射阻塞效应敏感参数
利用正弦波辐照受试雷达观察产生的实际效应,以此来选择阻塞效应敏感参数.具体的试验步骤如下:1) 开启雷达确保其正常工作,可在显示器上观察到目标回波成像;2) 设置信号发生器输出与受试雷达中心频率相同的正弦波,缓慢增加干扰功率,观察雷达单个扫描周期显示器目标成像并记录干扰功率p.
目标成像如图3所示.其中,图3a为无干扰时测试目标在雷达显示器上的成像,红色环形区域有较强回波,这是由地面反射造成的.在施加正弦波后,雷达环形回波区域出现由干扰源指向圆心的扇形空白区域,且扇形向外延伸至区域内测试目标回波面积大幅减小,将扇形空白区域称为干扰扇面[15],如图3b所示.其机理可解释为,在施加正弦波干扰后,干扰信号由受试雷达天线进入接收机,由(4)可知,此时有用信号增益下降、输出电平降低.雷达天线在一维转台的带动下保持匀速旋转,其主瓣与辐射天线主瓣方向逐渐相向,进入接收机的干扰电平增大,有用信号输出电平逐渐降低,直至低于系统自动检测门限,系统判断为“无目标”,显示器原目标成像处出现空白;随着角度的逐渐偏离,雷达受扰程度降低,有用信号增益上升,目标成像继续出现,因此空白区域呈“扇形”.另外,随着干扰功率的增加,原干扰扇面角度增加,测试目标的成像继续变小,时有时无,直至完全消失,且在不同方向上出现新的干扰扇面,如图3c~f所示.其机理为,干扰功率增加后,相同天线角度下进入接收机的干扰电平增加,导致干扰扇面角度增加;同时,从副瓣耦合进入接收机内部的干扰信号也可造成阻塞,形成新的干扰扇面.综上所述,可将正弦波辐照下受试雷达随干扰功率的变化总结如下:1) 雷达环形回波区域出现角度逐渐增加的由干扰源指向圆心的干扰扇面;2) 在不同方向出现新的干扰扇面;3) 目标成像逐渐变小,时有时无,直至完全消失.
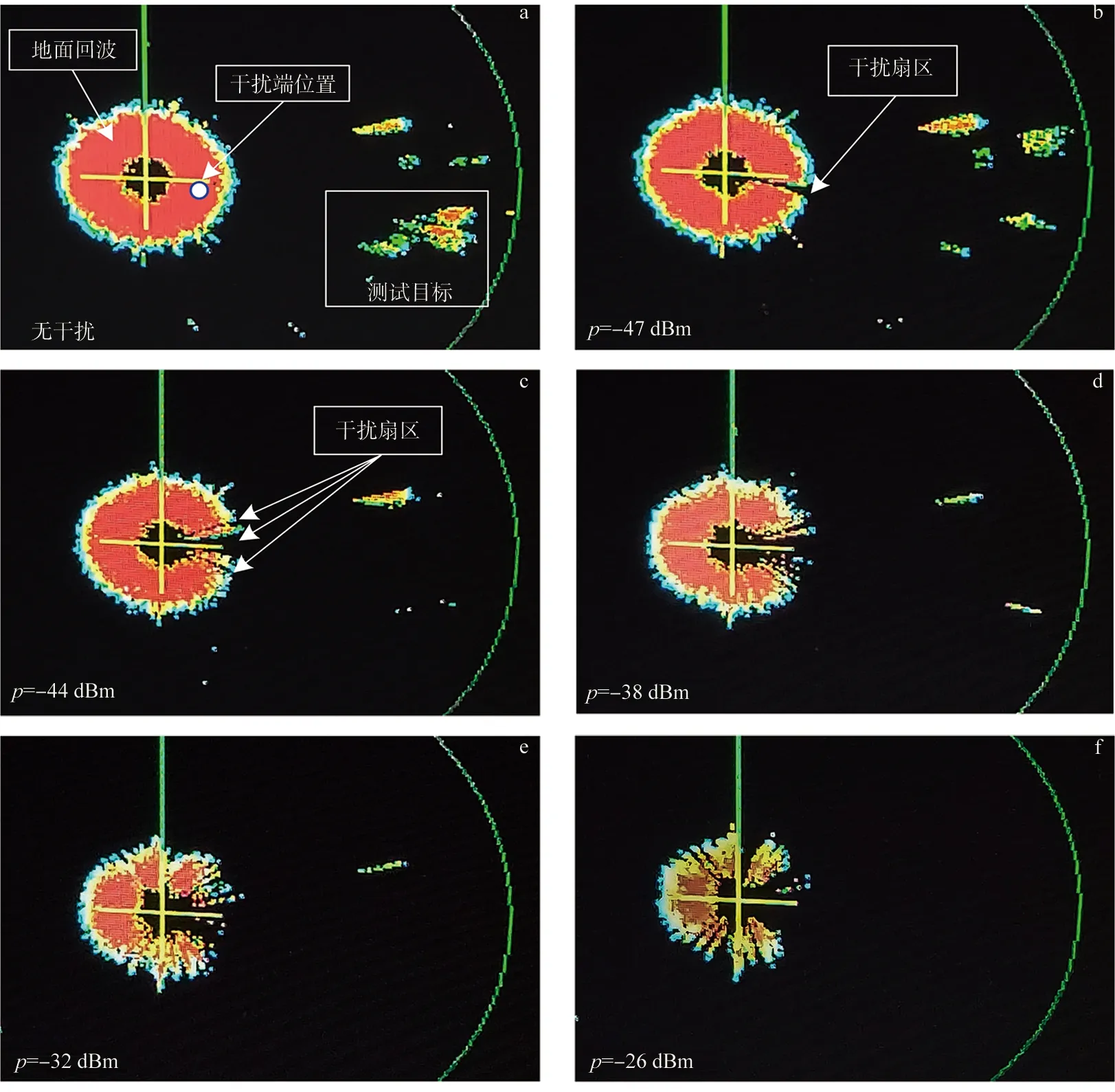
图3 不同强度干扰时目标成像Fig.3 Target Imaging Under Different Intensity Interference
基于上述第1种变化,可将是否出现特定角度指向圆心的干扰扇面作为阻塞效应敏感参数.然而,在屏幕上不易准确地判断干扰扇面是否出现,且其角度同样无法准确测量.以此为阻塞效应敏感参数,对于受试雷达而言可操作性不强,会引入较大的主观误差,难以满足需求.
基于上述第2种变化选择阻塞效应敏感参数,则每个新出现的干扰扇面都会面临前述问题,干扰扇面的数量也无法准确测定,同样不符合需求.
基于上述第3种变化做选择,可定义雷达单个扫描周期内目标成像完全消失为一次有效干扰,有效干扰概率为若干个扫描周期内有效干扰次数与总次数的比值.对于受试雷达的有效干扰可以通过目标成像准确地判定,有效干扰概率可以通过试验估测.有效干扰概率变化的实质是有用信号增益的变化,通过前述分析可知,决定有用信号增益的因素首先是雷达天线与辐射天线的相对位置,然后是干扰信号强度.选择有效干扰概率作为阻塞效应敏感判据,可有效避免位置因素的影响,直接建立其与干扰信号强度的关系,较客观地描述不同强度的干扰信号对雷达性能造成的影响.
2.3 电磁辐射阻塞效应敏感判据
已选定有效干扰概率作为阻塞效应敏感参数,通过试验研究其在不同功率、不同频率正弦波辐照下的变化规律,找出合适的敏感判据.具体试验布置如图2所示,方法如下:1) 开启雷达确保其正常工作,可在显示器上观察到目标回波成像;2) 设置信号发生器输出正弦波干扰信号,其输出功率不应对受试雷达造成影响;3) 调整信号发生器输出功率,每次调整后进行一定周期数的探测并统计其中未成像的次数,计算有效干扰概率,记录此时的干扰功率.
对于试验中探测周期数的设定,需要兼顾试验可操作性与减小误差的要求.扫描周期数取值过小时,结果偶然性太大;取值太大则会增加不必要的工作量.通过可重复性试验可知,扫描周期数选择20次时,试验结果可重复性较高,且不会大幅增加试验工作量,满足试验需求.结合受试雷达工作带宽为±40 MHz,选定干扰频偏Δfj=fj-f0(f0为受试雷达中心频率)为0,15,25,…,55 MHz,测得有效干扰概率随干扰功率的变化曲线如图4所示.
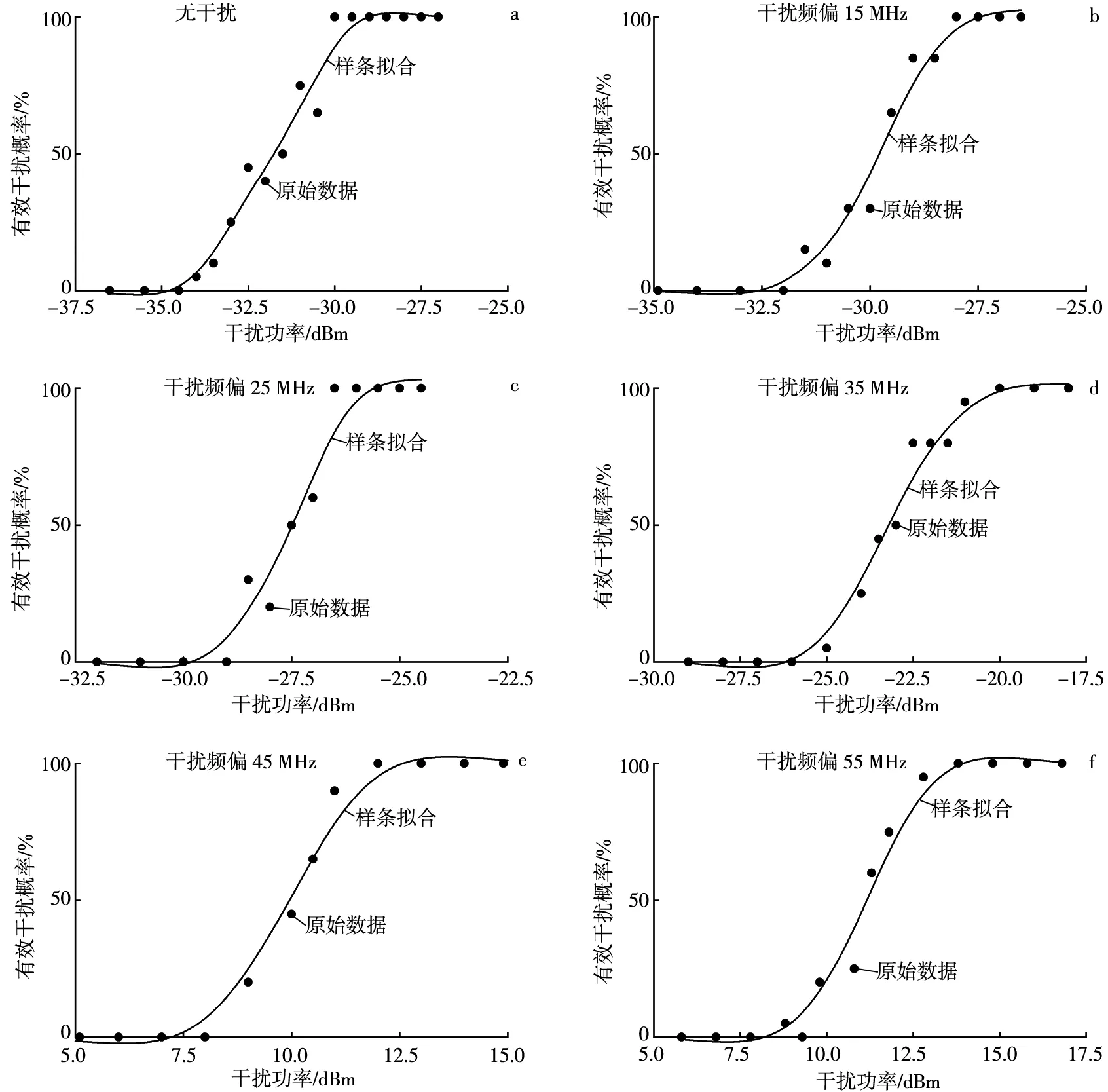
图4 有效干扰概率变化曲线Fig.4 Variation Curve of Effective Interference Probability
由图4可知,在不同的干扰频偏下,有效干扰概率与辐射功率的变化规律基本一致,即随着辐射功率的增强,有效干扰概率由0逐渐增大;其增长速率先升高后降低,直至雷达被完全阻塞.另外,当干扰功率相同时,在一定范围内,随着干扰频偏的增大,有效干扰概率呈明显降低趋势,符合一般认为的用频装备对带内干扰更为敏感的特性.
选择敏感判据侧重于试验的准确性与重复性,故对其要求为,在一定区域内,干扰强度的微小改变会引起受试设备工作性能的较大变化,即以“有效干扰概率/干扰功率”曲线斜率最大的点作为雷达阻塞效应敏感判据时误差最小.对拟合曲线进行插值,得到干扰源数组及对应的有效干扰概率数组,各点导数为
(5)
其中m=(xn-x1)/n.
通过计算所得有效干扰概率曲线最大斜率对应的有效干扰概率如表1所示,主要集中在47 %~62 %,平均值为54 %.由此可说明,在不同频偏干扰下,最敏感处的有效干扰概率较为接近,在54 %附近波动.为便于工程应用,可取有效干扰概率50 %作为电磁辐射阻塞效应敏感判据的理论值.另外,对于受试雷达而言,实际试验中很难出现恰好等于50 %的结果,可结合表1中数据提前设定控制误差,当试验步长小于控制误差时,若有效干扰概率处于40 %~60 %,即可将电磁干扰辐射电平作为雷达电磁辐射阻塞效应敏感电平;若此时试验结果未落入该区间,则取最接近区间两端的有效干扰概率对应电平均值作为雷达电磁辐射阻塞效应敏感电平.基于图4有效干扰概率曲线计算可知,若有效干扰概率达到40 %~60 %的任意值就判定为雷达受到有效干扰,其测试误差可控制在1 dB以内,具体数值如表2所示.
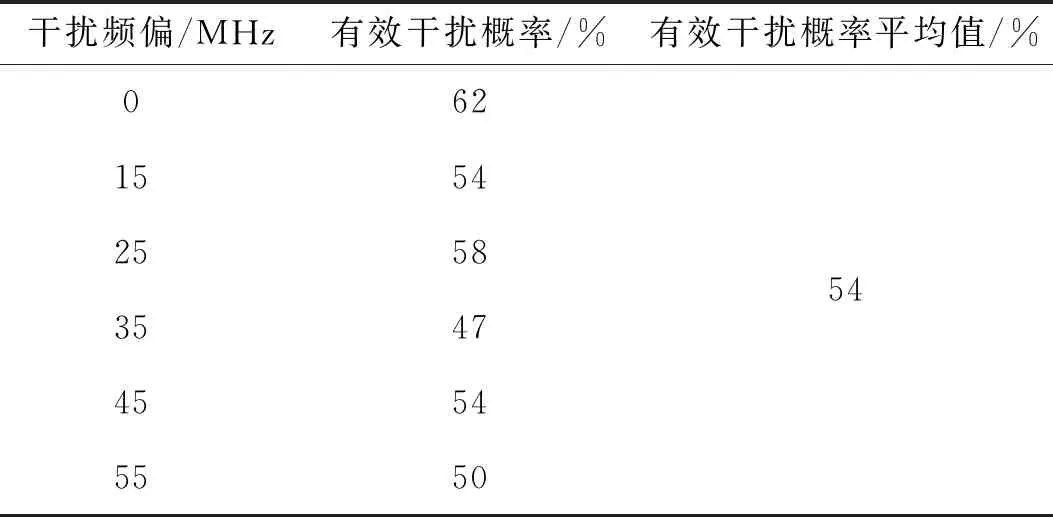
表1 斜率最大处的有效干扰概率Tab.1 Effective Interference Probability at the Maximum Slope
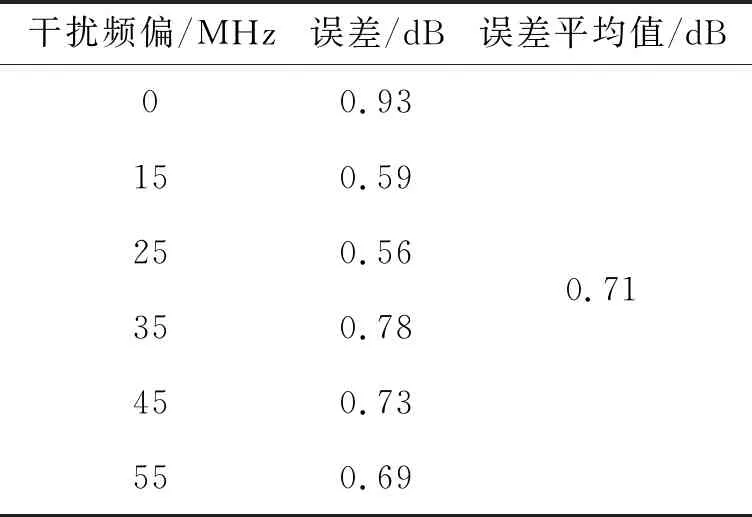
表2 有效干扰概率取40 %~60 %时的测试误差Tab.2 Test Error When the Effective Interference Probability Is 40 %~60 %
3 结 论
结合雷达电磁辐射阻塞效应的机理分析,从提高测试数据准确性、重复性出发,提出了受试雷达阻塞效应敏感判据,用于后续电磁辐射效应预测研究,具体结论如下.
1) 使用正弦波对雷达进行辐照,随着干扰功率的增大,雷达显示器上会出现干扰扇面,角度逐渐增加,数量变多;目标成像逐渐变小,时有时无,直至完全消失.
2) 将有效干扰概率作为受试雷达阻塞效应敏感参数,其在不同频率电磁辐射作用下的变化规律基本一致,具有普适性.
3) 分析试验结果,选定有效干扰概率50 %作为雷达电磁辐射阻塞效应敏感判据,当试验步长小于控制误差时,有效干扰概率处于40 %~60 %的电磁辐射干扰电平即可作为受试雷达的电磁辐射敏感电平(场强),以增强敏感判据的可操作性.
4) 所使用的对于敏感判据的研究方法可适用于其他型号雷达,所提出的敏感判据也可为研究其他型号雷达提供参考.
