一类流行性出血热周期模型的动力学分析
2022-05-10刘俊利
李 凤,刘俊利
(1.西安医学高等专科学校 基础部, 陕西 西安 710309;2.西安工程大学 理学院,陕西 西安 710032)
肾综合征出血热(hemorrhagic fever with renal syndrome,HFRS)[1],又称流行性出血热,其主要传染源是鼠类,潜伏期2周左右.流行性出血热是由汉坦病毒属各亚型引起的一类以发热、出血、肾功能损害等多种症状为临床表现的自然疫源性传染病.主要传播途径有动物源性传播、垂直传播和虫媒传播.根据其抗原结构基因特点,可分为至少40个亚型[2-5].其传染分布特点呈明显的地域性,且多发于秋冬季节.近几年的相关数据表明,中国是世界范围内流行性出血热疫情最重的国家[6],该疾病已严重影响人类的正常生活.
出血热的传染和爆发会随季节呈周期性波动[7].许多学者对具有周期性波动传染病的动力学行为进行了研究[8-11].研究成果主要集中在计算模型的阈值,利用阈值分析周期解的存在性和稳定性,讨论系统的一致持久性和灭绝性.国内对出血热的研究除了临床和统计学方面[12],还可以建立数学模型进而从数值模拟方面进行分析预测[13-15].本文中,笔者依据出血热具有周期流行的特点,在建立模型时考虑周期系数,建立一个非自治模型.
1 模型建立
根据图1中的仓室图建立如下模型:
(1)

图1 模型仓室图Fig.1 Compartment Diagram of Model
其中S(t),I(t)分别表示t时刻鼠群中的易感者、染病者.N(t)表示易感鼠和染病鼠的全体,即N(t)=S(t)+I(t),X(t)表示已具有传染性的出血热病毒(病鼠尿液污染或被病鼠啃咬过的食物等含有的病毒),A(t)为易感鼠的增长率,β1(t)为带病鼠对易感鼠的感染率,β2(t)为鼠释放的病毒对易感鼠的感染率,a(t)为染病鼠出血热病毒释放率,μ(t)为鼠的自然死亡率,σ(t)为病毒的清除率.A(t),β1(t),β2(t),μ(t),a(t),σ(t)是连续的正的ω-周期函数,ω>0.
显然,系统(1)的解是非负的.
引理1系统(1)的所有解最终有界且一致有界.
证由模型(1)易知
(2)
易证(2)有一个全局渐近稳定的正周期解
(3)
即
(4)
因此,(1)最终有界,由(1)中第3式可得X(t)最终有界.
对一个连续的ω-周期函数,定义
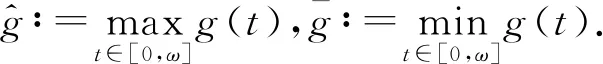



(5)
的基解矩阵,r(ΦB(ω))为ΦB(ω)的谱半径.由Perron-Frobenius引理,r(ΦB(ω))是ΦB(ω)的特征值,对应特征向量v*>0.

显然E0(t)=(N*(t),0,0)是模型(1)的无病周期解.下面根据文献[17],定义模型(1)的基本再生数.定义
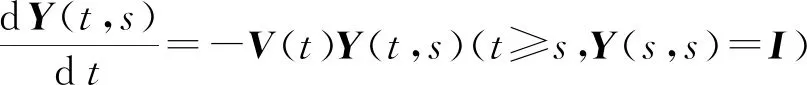
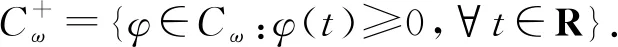
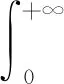
由文献[17],定义模型(1)的基本再生数为R0=r(L),其中r(L)代表算子L的谱半径.
定理1[17]R0满足如下结论:
1)R0=1⟺r(ΦF-V(ω))=1;
2)R0>1⟺r(ΦF-V(ω))>1;
3)R0<1⟺r(ΦF-V(ω))<1.
因此,当R0<1时模型(1)的无病周期解E0(t)=(N*(t),0,0)是局部渐近稳定的,当R0>1时不稳定.
2 疾病的灭绝和持久性
本节证明当R0<1时,无病周期解E0(t)=(N*(t),0,0)全局渐近稳定,说明疾病消失;当R0>1时,则疾病持续存在.
定理2当R0<1时,无病周期解E0(t)=(N*(t),0,0)全局渐近稳定,当R0>1时,它是不稳定的.
证由定理1,如果R0>1,则E0(t)=(N*(t),0,0)不稳定;如果R0<1,则E0(t)=(N*(t),0,0)局部渐近稳定,下面证明当R0<1时,E0(t)=(N*(t),0,0)全局吸引.
由(4)知,∀η>0,存在T>0,当t>T时,有N(t)≤N*(t)+η.当t>T时,由(1)得
考虑如下系统:



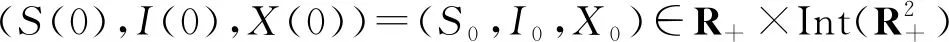

记M∂={(S0,I0,X0)∈∂Y0:Pm(S0,I0,X0)∈∂Y0,∀m≥0}.
下面证明
M∂={(S,0,0):S≥0}.
(6)
显然M∂⊇{(S,0,0):S≥0}.由模型(1)的第1式知S(t)>0,∀t>0.对任意的(S0,I0,X0)∈∂Y0{(S,0,0):S≥0},若I0=0,X0>0,因为
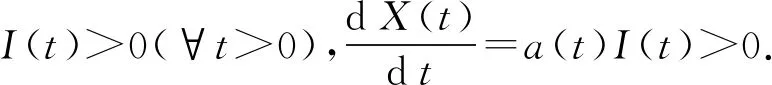

(7)



显然,M∂中的每个轨道收敛于E0,因此E0在M∂中是非循环的.通过文献[18]中定理1.3.1和注1.3.1得P相对于(Y0,∂Y0)一致持续,由文献[18]的定理3.1.1得(1)的解关于(X′,∂X0′)是一致持续的.

b(t)=β1(t)I(t)+β2(t)X(t)+μ(t),与S*(0)=0,矛盾.

3 数值模拟
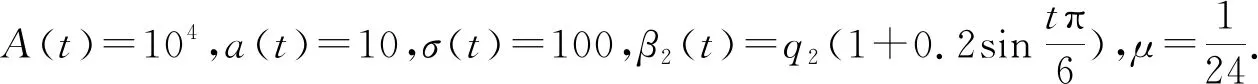
当q1=1.5×10-9,q2=2.4×10-9时,得R0=0.168 5<1,由定理2知,无病平衡点E0(2.4×105,0,0)是全局渐近稳定的,说明疾病绝灭.图2的a,b,c表示模型(1)的解随时间变化的曲线图.
当q1=1.5×10-7,q2=2.4×10-7时,得R0=8.797 1>1.由图3的a,b,c可知,疾病持续生存,系统的解趋向于一个正周期解,显示出血热疾病是持续存在的,与定理3结论一致,并且模型的解收敛到一个周期为12的正周期解.
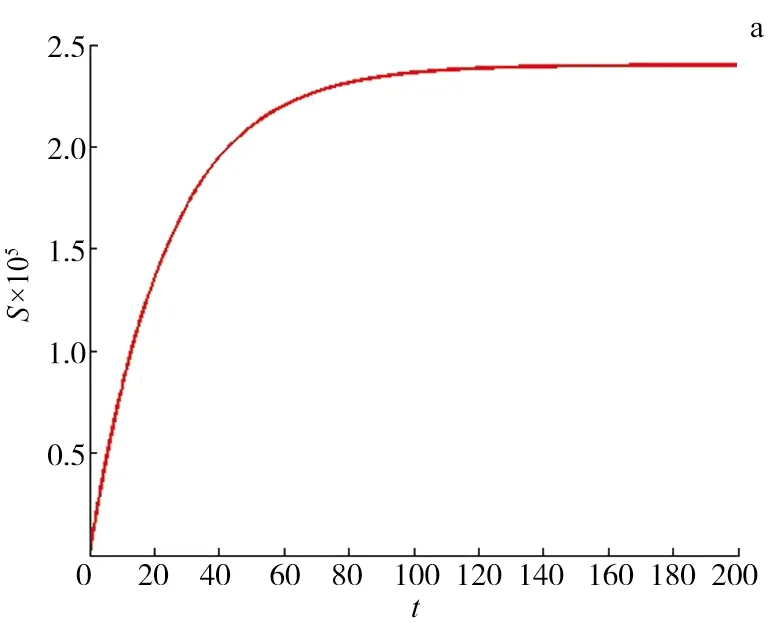

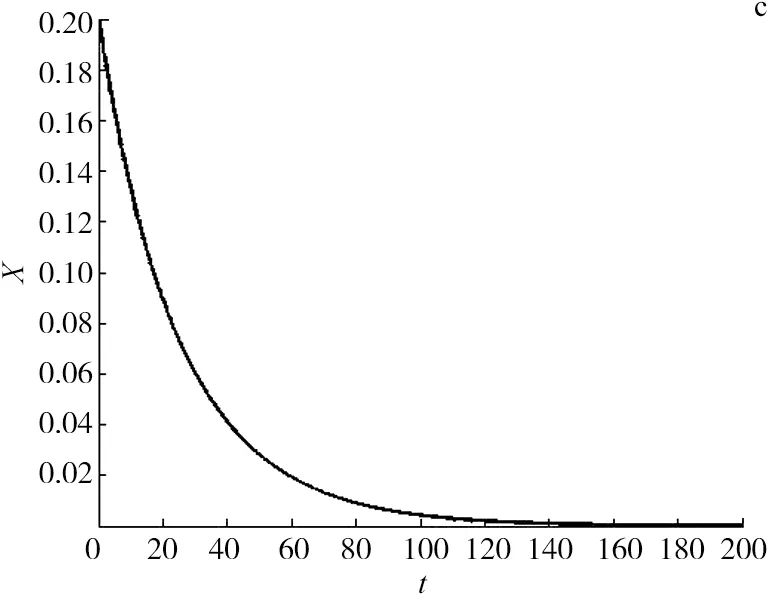
图2 当R0=0.168 5<1时,无病平衡点全局渐近稳定,疾病绝灭Fig.2 When R0=0.1685<1,the Diseas-free Peiodic Solution Is Glbally Asymptotically Stable and the Disease Dies Out


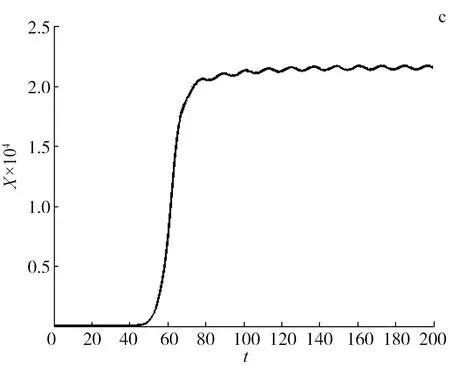
图3 当R0=8.797 1>1时,系统的解趋向于一个正周期解Fig.3 When R0=8.797 1>1 System Solution Tends to a Positive Periodis Solution
4 结 语
根据流行性出血热季节性爆发的特点,研究了一个周期的出血热疾病传播模型,模型的阈值通过积分算子的谱半径来定义,证明了无病周期解的全局稳定性和疾病的持久性.最后通过数值模拟验证了理论结果.数值模拟的结果表明,随着带病鼠对易感鼠的感染率,鼠释放的病毒对易感鼠的感染率的增加,出血热疾病会持续存在,疾病呈现周期震荡,因此清理环境.减少环境中的出血热病毒对控制出血热疾病是有利的.
