“先继承,再发展” 习题教学中科学思维的落实
2022-05-10北京
北京 郭 蕊
一、模型建构的落实
钱学森先生曾指出:“模型就是通过我们对问题的分解,利用我们考究得来的机理吸收一切主要因素,略去一切不主要的因素,所创造出来的一幅图画……”,也就是说,在模型建构的过程中,采用形象化的思维方式是最为有效的方法。中国科学院科普演讲团的王邦平老师曾提出物理模型解题法,该方法以“不变”的规范操作应对“万变”的高考试题,其操作程序如图1所示。学生只要长期按照模型解题法的操作步骤规范的解题,就能够摆脱背题、套公式的解题方法,从而真正做到用一套成熟的方法解决物理问题。为加强学生模型建构的能力,本文所采用的解题方法就是这套物理模型解题法。
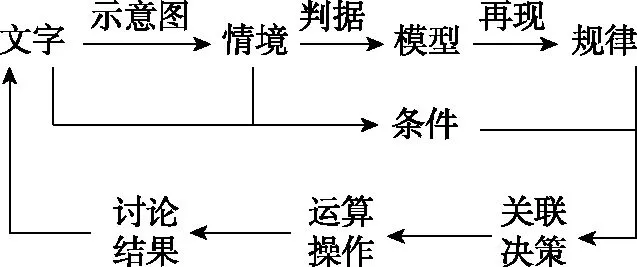
图1 物理模型解题法
1.对比相似物理过程,明确形象思维对模型建构的重要性
高三学生已经学习完高中所有的物理模型及规律,并建立了力学知识结构。但在相似物理过程的模型辨析上仍然有所欠缺,笔者在课前布置了两道学生易混淆物理过程的习题,课上安排不同的学生按照物理模型解题法的操作流程合作讲解这两道习题。甲同学讲解情境图的得出,乙同学讲解模型对应的规律及对应的条件,丙同学讲解如何挑选物理规律及最后的求解结果。
【例1】空间存在竖直向下,宽度一定的匀强电场E。质量为m,带电量为+q的粒子以水平初速度v0进入该电场,粒子离开电场时的偏转角度为θ,求粒子在电场中运动的竖直距离y及时间t。(不计粒子的重力)
甲同学:粒子受竖直向下的恒定电场力且有水平的初速度,模型为类平抛运动,情境图如图2所示。
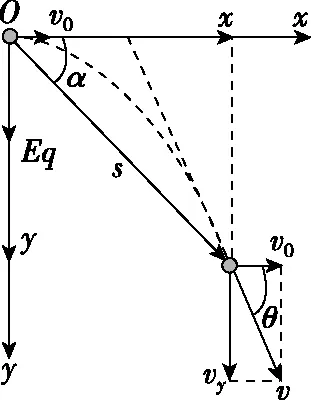
图2
乙同学:研究对象为单个物体,从牛顿运动定律结合运动学规律、动能定理分析,规律如下。直接条件有E,m,q,v0;间接条件有速度与水平方向的夹角θ。
模型:类平抛运动
牛顿运动定律结合运动学规律
水平:vx=v0(1)ax=0 (2)x=v0t(3)
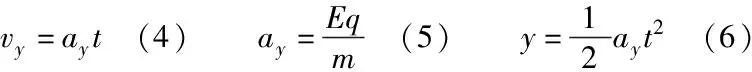
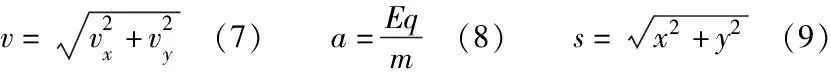

关系:tanθ=2tanα(12)

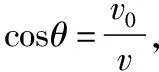
【例2】空间存在垂直纸面向外,宽度一定的匀强磁场B。质量为m,带电量为+q的粒子以水平初速度v0进入该磁场,粒子离开磁场时的偏转角度为θ,求粒子在磁场中运动的竖直距离y及时间t。(不计粒子的重力)
甲同学:粒子始终受到与速度方向垂直的洛伦兹力的作用,运动模型为匀速圆周运动,情境图如图3所示。
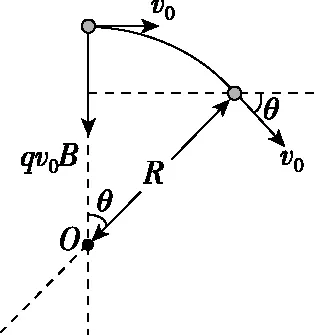
图3
乙同学:研究对象是单个物体,从牛顿运动定律结合运动学规律、动能定理分析,规律如下。直接条件有B,m,q,v0;间接条件有速度偏转角θ(匀速圆周运动中所对应的圆心角)。
模型:匀速(率)圆周运动
牛顿定律结合运动学规律
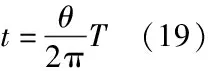
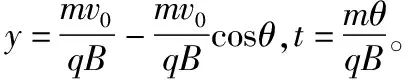
通过两道习题的讨论交流,让学生们再一次熟悉模型解题法的操作流程。虽然这两道习题的条件基本相同,但结果却截然不同。究其本质,是物理模型的不同。经过这样的对比,使学生们明确了形象思维对模型的确定起到了不可或缺的作用。
2.分析错因,提高物理知识与实践情境相联系的自觉性
相较于明确形象思维对模型建构的重要性,如何提高学生把物理知识与实践情境相联系的自觉性,才是重中之重。笔者采取分组讨论的形式,请学生将两道习题做错的原因填到错题错因分析表里,再进行全班汇总。两道例题都没有涉及运算操作后讨论结果的思维过程,所以在表中不加以分析。
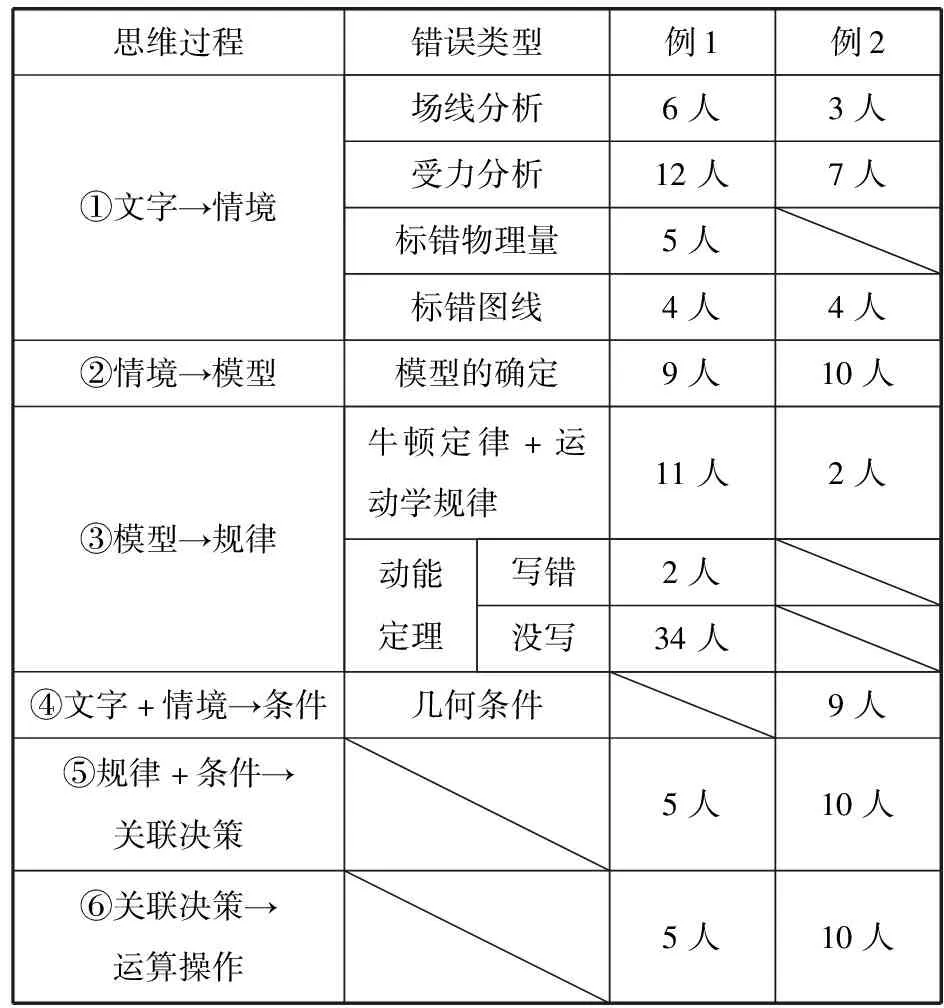
错题错因分析表
通过统计,学生已经能初步认识到情境图错误、规律书写时没有考虑动能定理是最为常见的两种错误。同一人在同一操作步骤中若出现多次错误,错误人数应记为1。未考虑动能定理的学生,不能确定书写后是否有误,错误人数不累计。整理出错题错因分析柱状图,如图4所示。
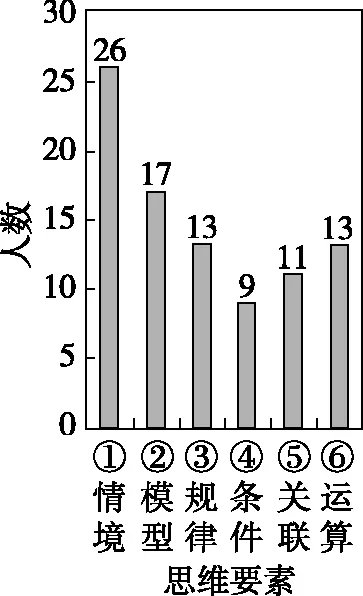
图4 错题错因分析柱状图
通过图4,学生能更直观的汇总错因,得知大部分问题都出现在了情境图上。在讨论的过程中,也有很多学生意识到例题1情境图出错,还会导致后续模型判定出问题;例题2情境图出错,也会导致找不到本题特定的几何条件。让学生们自己意识到问题的根源所在,提高他们把物理知识与实践情境进行联系的自觉性。
随后,教师引导学生从呈现在卷面上的表达形式总结每道例题的得分点,学生总结为“模型对应的规律”“本题的条件”“对照条件挑选规律后的运算操作”,这就进一步明确了习题的功能结构——“模型+条件+算法”。
二、质疑创新的落实
虽然已经有很多教师对高中物理习题教学进行了大量的研究,并且都致力于让学生们摆脱题海战术。但是,怎么才能真正达到“一题多解”“一题多变”“多题归一”呢?在解决文中两道例题的过程中,有的学生选择用不同的物理规律解决问题,这本质上就是“一题多解”。
对于“一题多变”,教师需要给学生一定的指导。由于习题是按照“模型+条件+算法”的结构组成的,在不改变模型的条件下,教师让学生以小组为单位,改编这两道习题。小组展示只需要说明改编的题干,画出情境图发生的变化,以及改编的条件和挑选好的规律。
【改编例题1】如图5所示,空间存在竖直向下的匀强电场E,在电场中有一固定的斜面,斜面与水平面的夹角为θ。质量为m,带电量为+q的粒子以初速度v0沿水平方向射出,恰好垂直地射到固定的斜面上,求该粒子落到斜面时的速度v。(不计粒子的重力)
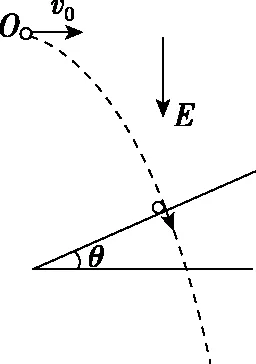
图5
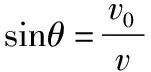
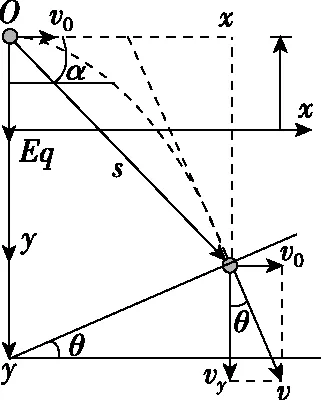
图6
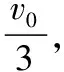

图7
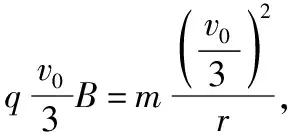
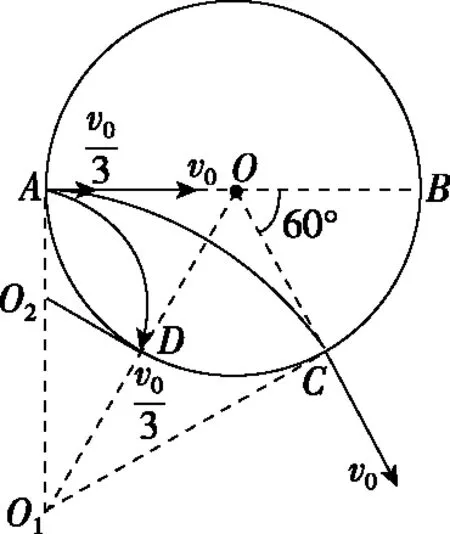
图8
改编例题的过程,学生能进一步体会习题的功能结构“模型+条件+算法”。展示改编题的过程,不仅能够提高学生按操作流程解题的自觉性,而且能够让他们认识到只要习题对应的条件发生了改变,所挑选的规律就会随之发生变化,结果自然就会不同。通过这样的感悟,学生可以真正理解“一题多变”的含义,进而落实提升质疑创新能力。
通过本文中的习题教学,学生们对习题一定有了更新的认识,教师将小结留在作业中,让学生有更大的思考空间。在汇总了大量学生的课后反思后,笔者发现大部分学生都能够清晰地认识到情境图的重要性。无论题目是否改编,习题的基本框架都是“模型+条件+算法”,很多习题实际上就是同一个模型变换了各种各样的条件而已。通过课后长时间的内化环节,学生完成了对“多题归一”的理解。
三、结束语
按照习题的功能结构“模型+条件+算法”,可将习题考查点总结为三大类。第一类考查的是学生的建模水平,模型建构除了本文中由运动画出情境图的类型外,还包括依据文字描述一步步抽象画出情境图并判断出相应模型的类型。第二类考查的是学生依据特定条件关联规律的水平,本文中的习题对应的条件相对简单,从文字中就可得出相应条件,更复杂的条件则涉及了画出准确的情境图得出习题特定条件的类型。第三类考查的是学生依据标、矢量运算,结合数学知识得出结论并讨论结果的水平,本文中并没有涉及到复杂运算及讨论结果的过程。

