高速铁路路基粗粒土填料动静力力学特性试验研究

2022-05-10王天亮宋宏芳卜建清尹赵爱

铁道学报 2022年4期

王天亮，张飞，宋宏芳，卜建清，尹赵爱

(1.石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室, 河北石家庄 050043；2.石家庄铁道大学道路与铁道工程安全保障省部共建教育部重点实验室, 河北石家庄 050043)

我国高速铁路的不断发展，列车速度的不断增加，对轨道结构稳定性和平顺度的要求越来越高，对路基填料性能也提出了更高的要求。粗粒土填料近些年被广泛地应用在诸多工程中，例如，砂石坝、铁路、公路工程，主要得益于其优越的力学性能。路基作为铁路线路的重要组成部分，具有承担上部结构自重和列车运行中产生的动荷载冲击的作用。细粒含量和含水率对粗粒土的力学性能有着重要影响，特别是不同细粒含量的粗粒土往往呈现不同的力学性能，所适用的工程特征也不尽相同。

在粗粒土静动力学特性研究方面，目前主要以试验和数值仿真等方法为主[1]。在粗粒土填料静力学特性研究方面，彭勃等[2]对红砂岩粗粒土的压实特性进行了研究，分析了压实厚度和能量对粗粒土压实特性的影响。陈乐求等[3]对改良粗粒土的静动力强度进行了深入研究，研究结果表明，水泥改良后的泥质板岩粗粒土静动力学性能明显提高。冷伍明等[4]借助大型三轴剪切试验，分析了重载铁路路基粗粒土填料的力学性能。杨尧[5]、刘轶[6]分别对低围压条件不同压实度、含水率和排水条件下的粗粒土静力特性进行了研究，分析了粗粒土的应力-应变曲线特征。

由于路基承受上部列车长期动荷载的冲击作用，许多学者进一步开展了粗粒土填料动力特性相关研究，对于粗粒土的动力特性研究多集中在应力-应变关系[7-8]、动弹性模量[9-10]和累积塑性变形[11-12]等方面。冷伍明等[13-14]分析了粗粒土填料临界动应力和累积塑性应变随围压和含水率的变化规律。梅慧浩等[15]、周文权等[16]针对动荷载作用下重载铁路路基粗粒土填料的累积塑性应变特征进行了分析，建立了相应的塑性应变预测模型。Zhai等[17]提出一种预测饱和粗粒土临界动应力的经验方法。Zhang等[18]研究了低温条件下不同粗粒含量粉土的动静力特性，认为粗粒土的含量对于冻土混合料的动静力特性有较大影响。Mei等[19]通过分析粗粒土的累积塑性应变特征，建立了考虑不同应力状态和轴向加载次数的塑性应变预测模型。以上研究可以看出，针对不同水分和温度条件下的粗粒土动力特性研究较为深入，但是关于不同细粒含量下粗粒土的动力特性研究相对较少。

综上所述，本文开展不同含水率和细粒含量下粗粒土的动静力学特性试验研究,分析在不同静荷载和围压下粗粒土的应力-应变特征、变形模量以及抗剪强度。同时，考虑反复动荷载作用下，研究不同围压和动应力幅值下粗粒土应力-应变滞回曲线变化规律，分析粗粒土动弹性模量和累积塑性变形特征。研究结果可为高速铁路粗粒土路基设计和早期病害发现提供重要依据。

1 试验方案

1.1 试验材料与设备

本次试验选用细圆砾土路基填料，颗粒粒径最大为20 mm，粒径大于2 mm的颗粒质量超过总质量的50%，粗颗粒形状以浑圆为主，属于AB组路基填料。其中，粒径小于0.075 mm的细粒土液限含水量为23.8%，塑性指数为8.77，塑限含水量为15.03%。

选取细粒占比分别为5%、10%和15%的粗粒土填料[20-21]，开展动力性能试验，颗粒级配曲线和基本物理指标如表1和图1所示。由表1可知，随着细粒含量的增加，粗粒土的最大干密度先增大后减小[22]，这主要是由于细颗粒填充粗颗粒孔隙，单位体积粗粒土干土质量增大，干密度随之增加；当细颗粒超过一定含量后，细颗粒将占据粗颗粒的空间，粗颗粒减少，单位体积粗粒土干质量减少，干密度随之降低。

表1 粗粒土的最大干密度和最优含水率

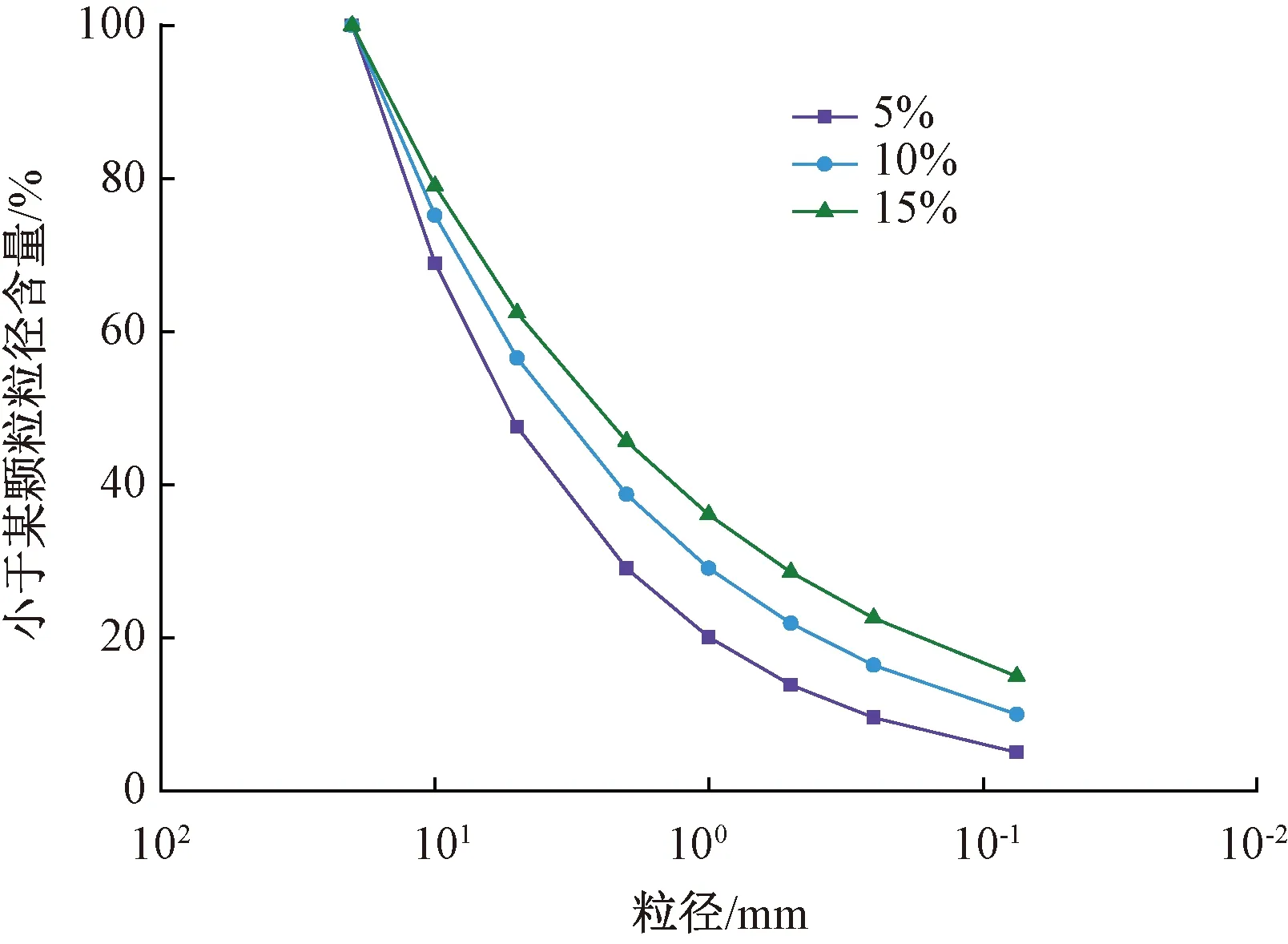
图1 粗粒土颗粒级配曲线

试验采用GDS动静三轴仪。静力试验的加载运用应变控制方式，在加载过程中速率取值为2 mm/min，当试样变形达到15%后停止试验。试验过程考虑三种不同的含水率，分别为4%、6%和8%。

动力加载采用应力控制循环加载方式，施加正弦波形轴向循环应力，循环次数最大值设定为50 000次，根据高速铁路列车运行速度和车长，计算得到荷载频率为5 Hz，动荷载应力幅值最大取120 kPa(表2)。试验时使用压力传感器采集循环荷载，使用位移传感器采集试样轴向变形。当试样的轴向累积应变达到5%，或试验循环次数达到预先设定的50 000次时，结束试验。

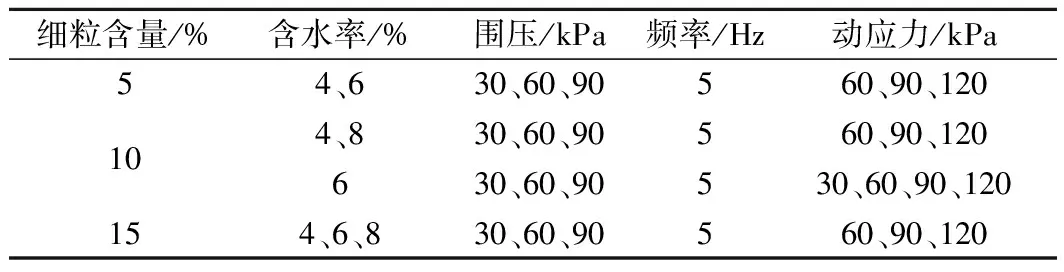
表2 粗粒土动力特性试验参数

1.2 试样制备及安装

在试样制作过程中，采用控制干密度法分三层击实试样。试验前称取对应质量的各种粒径的土颗粒，搅拌均匀，配制预先设计的含水量，试样尺寸为直径100 mm、高度200 mm，配制好的试样用保鲜膜密封24 h。试样制备好后，将试样放至于三轴试验压力室中，通过注水的方式施加围压。轴向力施加时，由于试验装置压力室不透明，不能直接进行位移控制，因此，先采用试接触的方式让加载轴与试样紧密接触，故设定0.01 kN接触力作为控制接触条件，当轴向力达到该值且稳定后，位移值清零，启动试验加载程序。

1.3 围压施加及排水条件

依据铁路路基填料原位应力条件，反映在试验中主要包含固结压力σ3、固结应力比Kc等指标。考虑基床结构周围所受压力较低，根据相关研究对路基围压实测值，试验围压最终选取为30、60、90 kPa[23]。

试验所用试样为按照要求击实的粗颗粒料，在试验过程中不考虑固结问题。考虑基床填料埋深较浅，且列车荷载作用具有瞬时特性，造成一定深度内基床填料的水来不及排出。因此，不考虑填料的排水问题，试验条件为不固结不排水。

2 静力特性分析

2.1 不同含水率条件下应力-应变关系曲线

图2～图4为粗粒土应力-应变曲线。由图可知，随着含水率的增加，偏应力总体呈下降趋势。试样含水率为4%，当应变为1.5×10-2～3.3×10-2时，试样达到最大强度；当试样含水率上升为6%时，峰值强度有所降低，峰值强度所对应的应变为2.8×10-2～4.2×10-2；含水率分别为4%和6%时的应力-应变曲线呈现出先增大后减小的趋势；当试样含水率为8%时，随着应变增加，应力呈现出先增大后逐渐趋于稳定的特征，试样呈现出应变硬化特性。这主要是由于随着土体中自由水含量增多，水对颗粒起到润滑作用，加剧了颗粒间的相对运动，导致试样强度降低。随着含水率的升高，应力-应变关系曲线由软化型逐步过渡到硬化型。

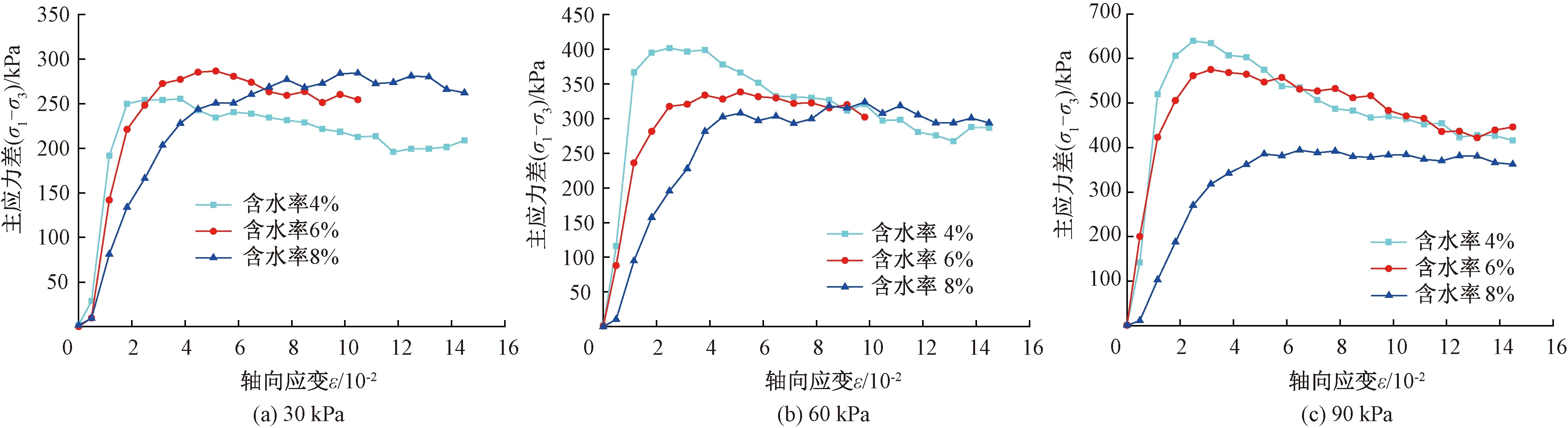
图2 细粒含量为5%的粗粒土应力-应变曲线

随着围压的增大，偏应力逐渐增大，在含水率和细粒含量相同的条件下，不同围压下粗粒土的应力-应变曲线具有相似的变化趋势。同时，在低含水率条件下，围压对于增大土体强度的作用效果较为明显，随着含水率的增加，围压对粗粒土强度的影响减弱。这主要是由于围压对土体的侧向约束作用，导致颗粒间的咬合力增大，限制了土体的侧向变形，进而土体强度增大。含水率增加至一定程度时，粗粒土颗粒间的摩擦力和咬合力减小，致使围压的作用减弱。

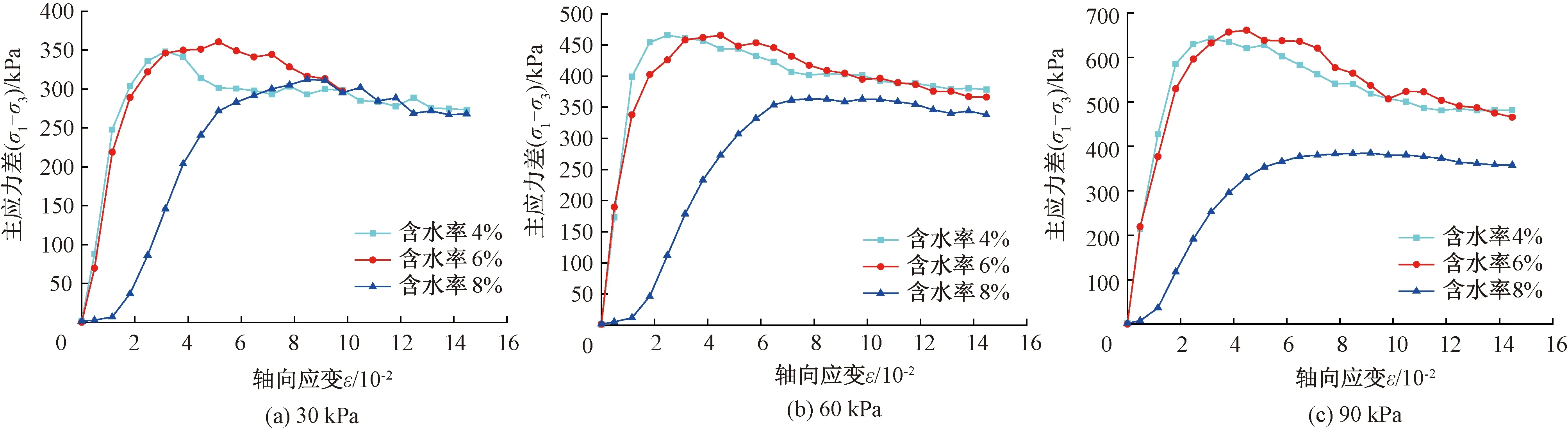
图3 细粒含量为10%的粗粒土应力-应变曲线

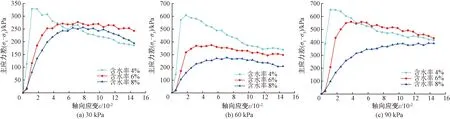
图4 细粒含量为15%的粗粒土应力-应变曲线

对于不同细粒含量的粗粒土而言，在相同的含水率和围压作用下，细粒含量为10%的试样抗剪强度高于其他两种试样。由此可见，当细粒掺量为10%时，粗粒土试样可以形成最优的配比组合[24]，此时，粗粒土试样抗剪强度达到最大。这主要是由于当细粒含量较小时，粗颗粒间的孔隙不能被填满，粗粒土之间的黏结力较小。随着细颗粒含量不断增多，细颗粒逐渐充满了粗颗粒之间的孔隙，随着细颗粒含量继续增加，细颗粒会将粗颗粒包裹，粗颗粒间摩擦力减小，导致另外两种情况粗粒土的抗剪强度相对较低。

2.2 变形模量特征

采用割线模量法[25]，计算粗粒土的变形模量。其中，对应力-应变软化型试样，变形模量采用其峰值点进行计算；对于没有明显峰值点的试样，变形模量计算选取应力-应变曲线上的转折点，略有波动或应力不再增大的点进行变形模量计算[26]。对于硬化型无峰值点的应力-应变关系曲线，取轴向应变0.06对应的主应力差作为峰值强度进行分析。由此得到不同含水率与变形模量之间的关系曲线，如图5所示。

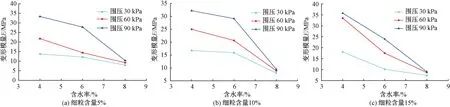
图5 变形模量与含水率关系曲线

由图5可看出，随着含水率的增加，粗粒土变形模量逐渐减小，变形也逐渐增大；细粒含量为10%，含水率由6%增加到8%时，变形模量急剧减小。由于围压对试样轴向变形具有一定的抑制作用，因此，变形模量则随着围压的不断增大而增大，但在含水率不断增大的情况下，围压对变形模量的影响作用逐渐减小。含水率为4%和6%时，围压对试样的径向抑制作用导致变形模量受围压影响较大。当试样细粒含量不同时，在同一围压下，变形模量随着细粒含量增大而增大；当含水率为8%时，围压对变形模量影响不明显。细粒含量为15%的粗粒土试样变形模量比其他细粒含量大，说明在一定条件下细粒含量增加有利于提升粗粒土抵抗变形的能力。当含水率为8%时，细粒含量对粗粒土试样变形模量影响不大，表明此时含水率是影响变形模量的主要因素。

2.3 抗剪强度参数

为分析粗粒土的抗剪强度，采用摩尔库伦准则求得粗粒土的黏聚力c以及内摩擦角φ，见表3。

表3 粗粒土的剪切强度指标

由表3中数据可知，粗粒土内摩擦角随含水率的增大而逐渐减小，但土体的黏聚力变化则正好相反。含水率增加导致细粒土中自由水含量增大，细颗粒的润滑作用降低了粗颗粒之间的咬合力和摩擦力，致使粗粒土的内摩擦角降低；然而，在有限的含水率条件下，细颗粒之间的黏聚力和结合水占据主导作用，且粗颗粒之间的孔隙被细颗粒充填，粗颗粒之间的黏结性在一定程度上发生了改变，致使粗粒土试样黏聚力增大。相同含水率情况下，内摩擦角随细粒含量的增加变化不大，黏聚力先增大后减小，在细粒含量为10%时黏聚力最大，表明细粒含量可以有效地提高粗粒土黏聚力，且存在一个最优的细粒含量值。

3 动力特性分析

3.1 累积塑性应变

安定性理论可以用来描述颗粒状材料的累积变形，基于该理论，轴向累积变形分为增量破坏、塑性蠕变和塑性安定三个范围，如图6所示[27]。

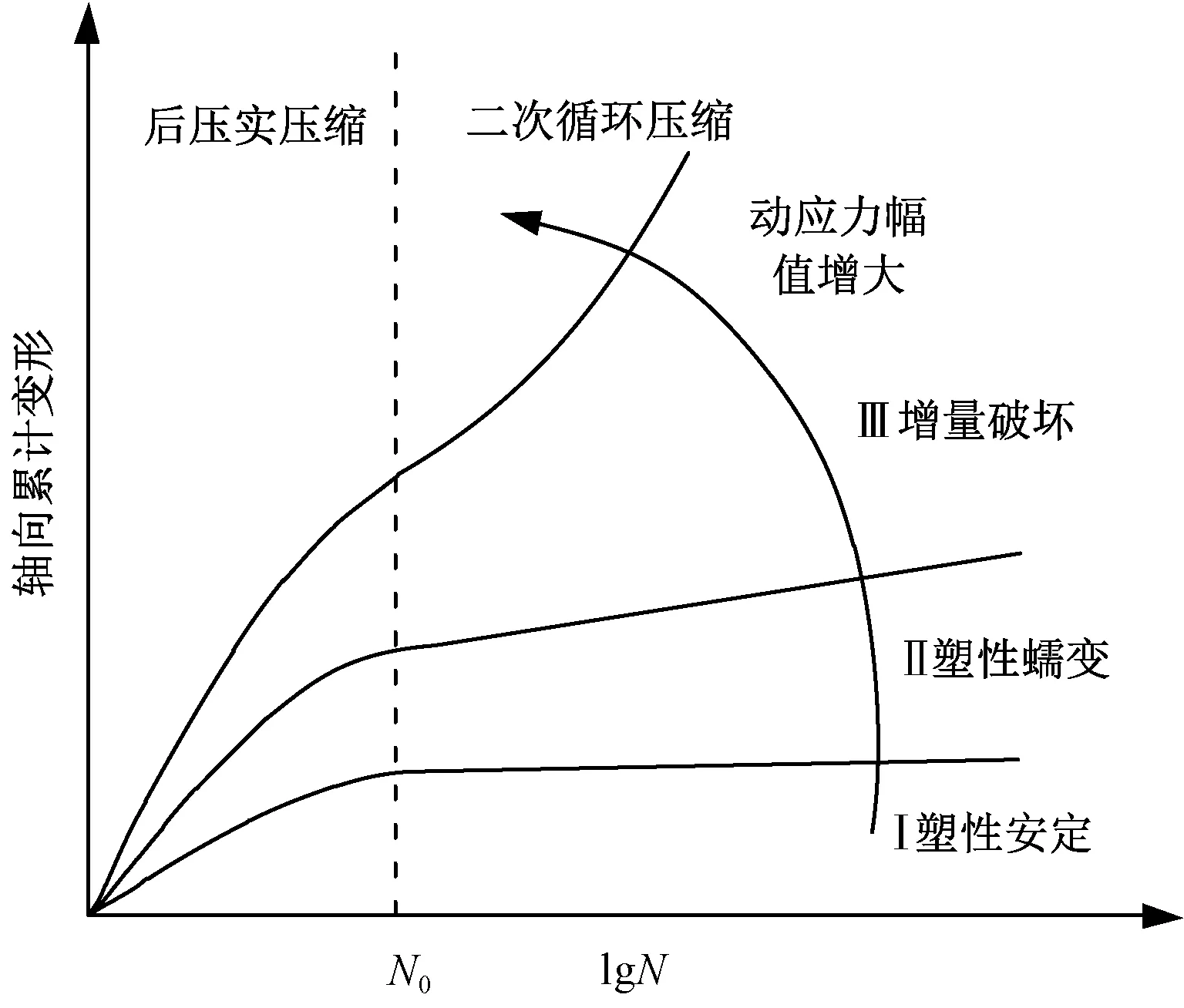
图6 不同动应力荷载下轴向累积变形与循环次数关系

为进一步对每个范围进行量化，Chen等[27]对安定范围标准进行了定义。

其中，1/as为图7所示三种累积应变曲线拟合曲线的斜率[27]。

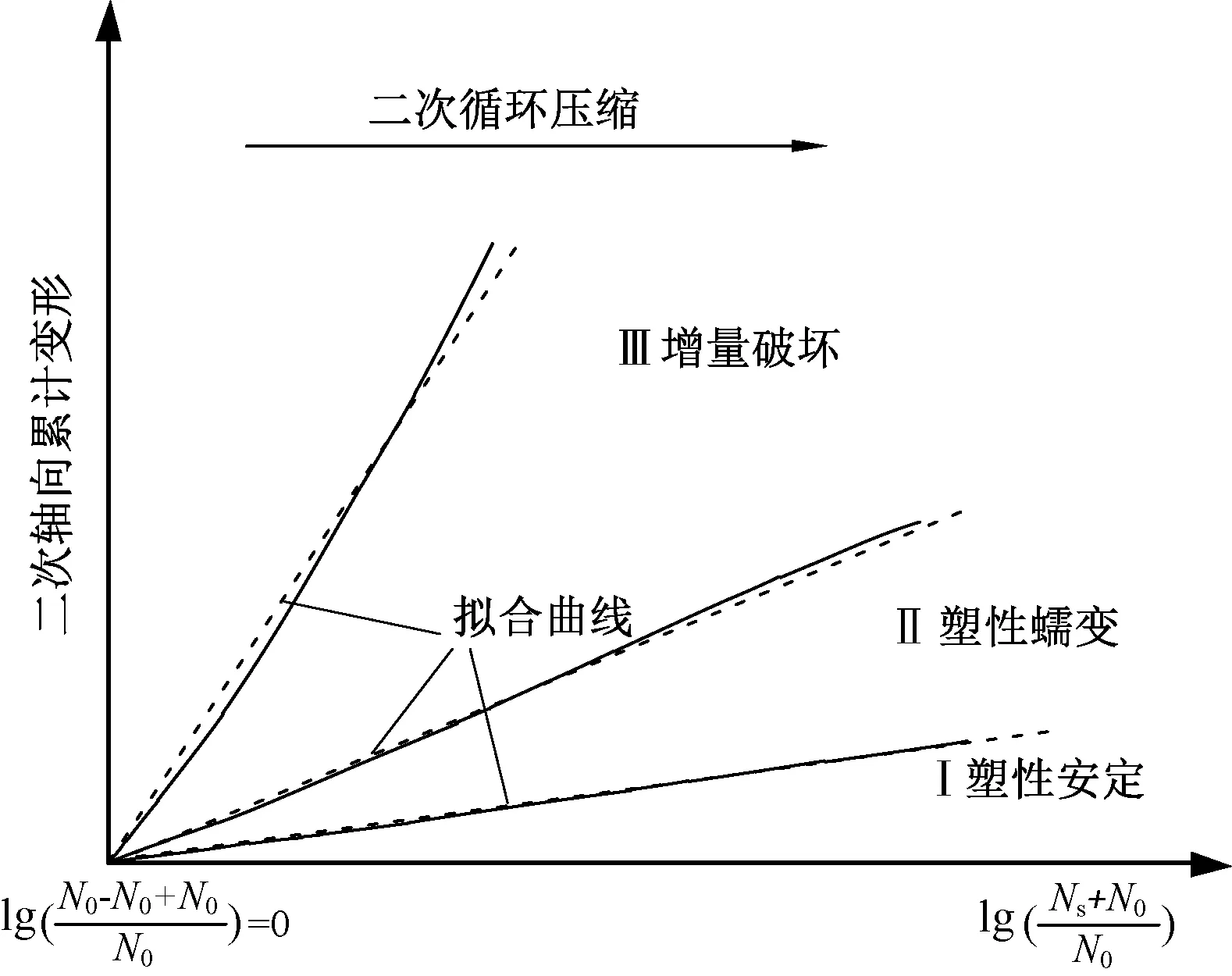
图7 二次变形与二次循环压缩次数关系示意

围压为60 kPa，细粒含量为10%时，不同含水率及动应力幅值下轴向累积应变与加载次数关系如图8所示。细粒含量分别为5%和15%的粗粒土在围压为30 kPa，含水率为6%条件下，不同动应力幅值下轴向累积应变与加载次数关系如图9所示。

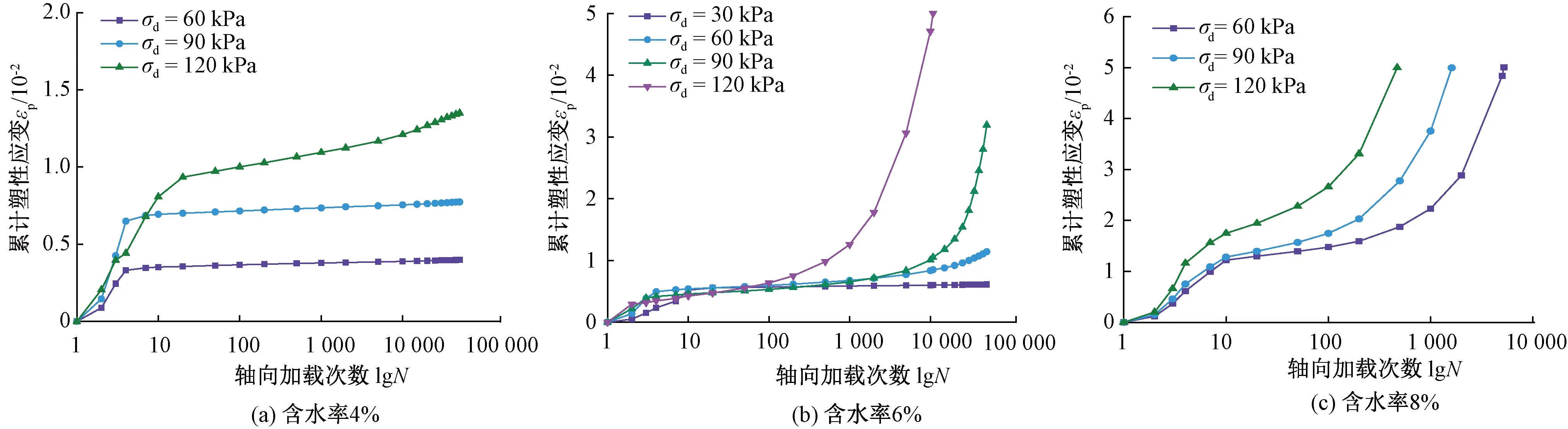
图8 细粒含量为10%、围压为30 kPa时，累积塑性应变与轴向加载次数曲线

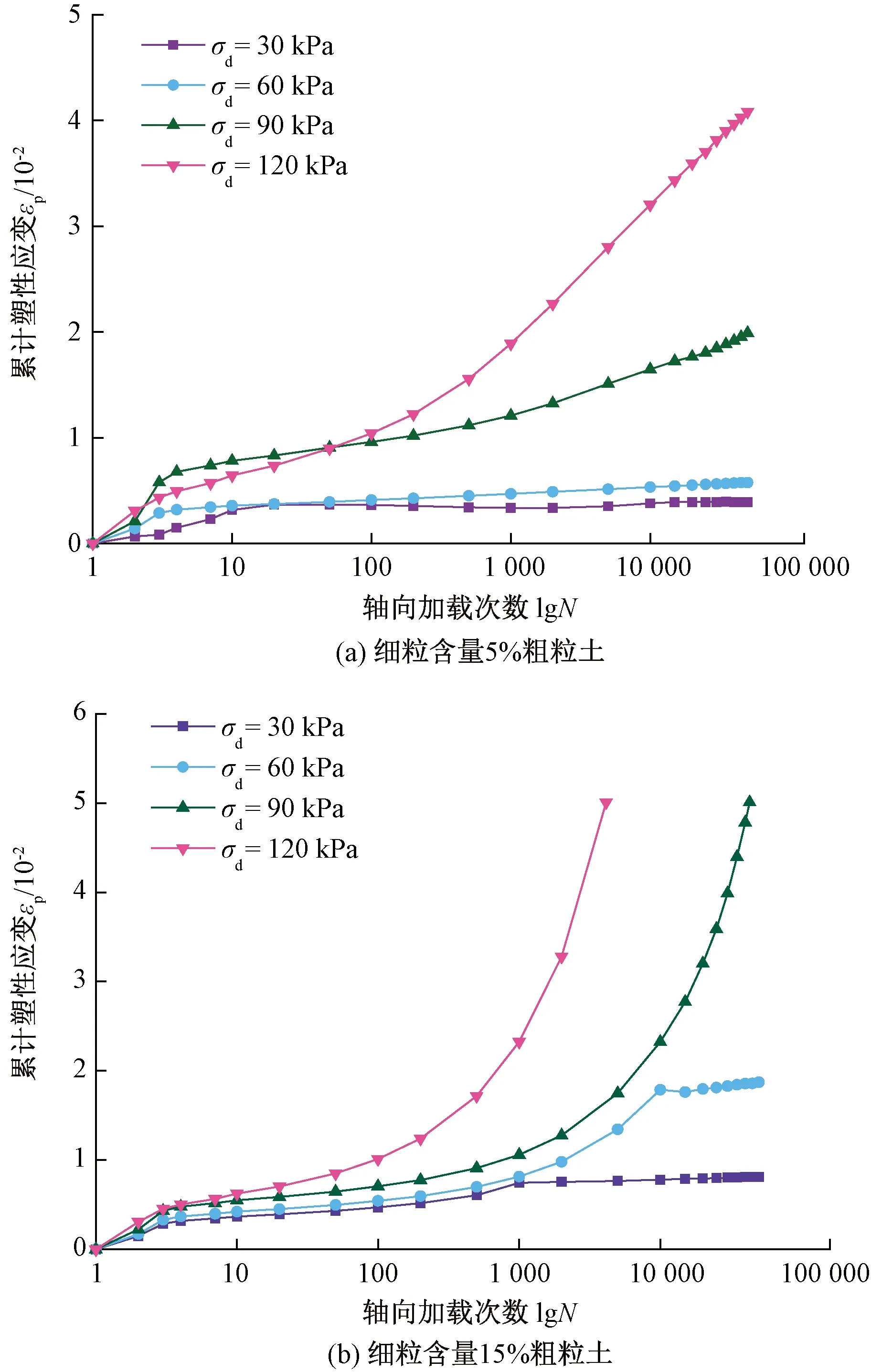
图9 含水率为6%、围压为30 kPa时累积塑性应变与轴向加载次数曲线

由图8可以看出，含水率4%条件下，动应力分别为60 kPa和90 kPa时，土体处于塑性安定范围，土体的累积变形稳定在0.35%～0.70%。随着动应力的进一步增大，土体逐渐过渡到塑性蠕变范围。当含水率增加到6%时，试样逐渐过渡到塑性蠕变范围(动应力幅值为60 kPa)，或处于增量破坏范围(动应力幅值分别为90、120 kPa)。当含水率达到8%时，试样全部处于增量破坏范围。

此外，处于塑性安定范围和塑性蠕变范围内的试样，前10个轴向加载周期会出现较大的累积轴向变形，累积轴向变形接近50%。对于已经位于增量破坏范围的土样，达到破坏标准时所需要的轴向加载次数随着动应力幅值的增加而逐渐减小。在较低的含水率下，较小的动应力幅值使轴向累积变形增加缓慢；在较高的含水率下，轴向累积变形增加显著。

由图8(b)和图9可以看出，不同细粒含量与较低动应力幅值条件下，累积塑性应变先增大后趋于稳定。动应力幅值的不断增大，累积塑性应变随着加载次数的增大而明显增大。细粒含量为5%，且动应力幅值σd分别为30、60 kPa时，粗粒土试样处于安定范围内；随着动应力幅值增大(90 kPa时)，粗粒土试样处于塑性蠕变范围内；当动应力为120 kPa时，土体逐渐过渡到增量破坏范围。当试样细粒含量上升至10%，施加的动应力幅值为60 kPa时，粗粒土试样处于塑性蠕变范围内，但塑性蠕变与增量破坏之间的界限未能明确；随着动应力幅值继续增大(大于90 kPa)，粗粒土试样位于增量破坏范围内。当细粒含量为15%，且动应力幅值分别为30、60 kPa时，粗粒土试样位于安定范围内；当动应力幅值持续增大(大于90 kPa)，粗粒土试样则直接跃至增量破坏范围。在此过程中，塑性蠕变范围不能明确得知，究其原因主要是试验所施加的动应力幅值跳跃较大，导致了塑性蠕变范围边界值缺失。综上可知，相同含水率条件下，细粒含量为5%的粗粒土抵抗塑性变形能力较好。

3.2 滞回曲线

图10给出了细粒含量为15%，围压为30 kPa，加载次数为10 000次，动应力幅值分别为30、60、90、120 kPa时，粗粒土的动应力-应变滞回圈曲线。由图10可知，动应力幅值分别为30、60、90 kPa时，动应变分别为0.29×10-2、0.31×10-2、2.32×10-2，试样均未达到破坏标准，动应力幅值为120 kPa时，试样出现破坏。可以看出，随着动应力幅值的增大，在相同的加载次数下动应变逐渐变大。但随着动应力幅值的增大，试样破坏时所需的加载次数逐渐减小。前10次的加载滞回曲线随着动应力幅值的增大逐渐密集，主要是由于随着动应力幅值增大，粗粒土初期压实速度逐渐变快，在较低的动应力幅值作用下初期压实需要更多次的循环加载。

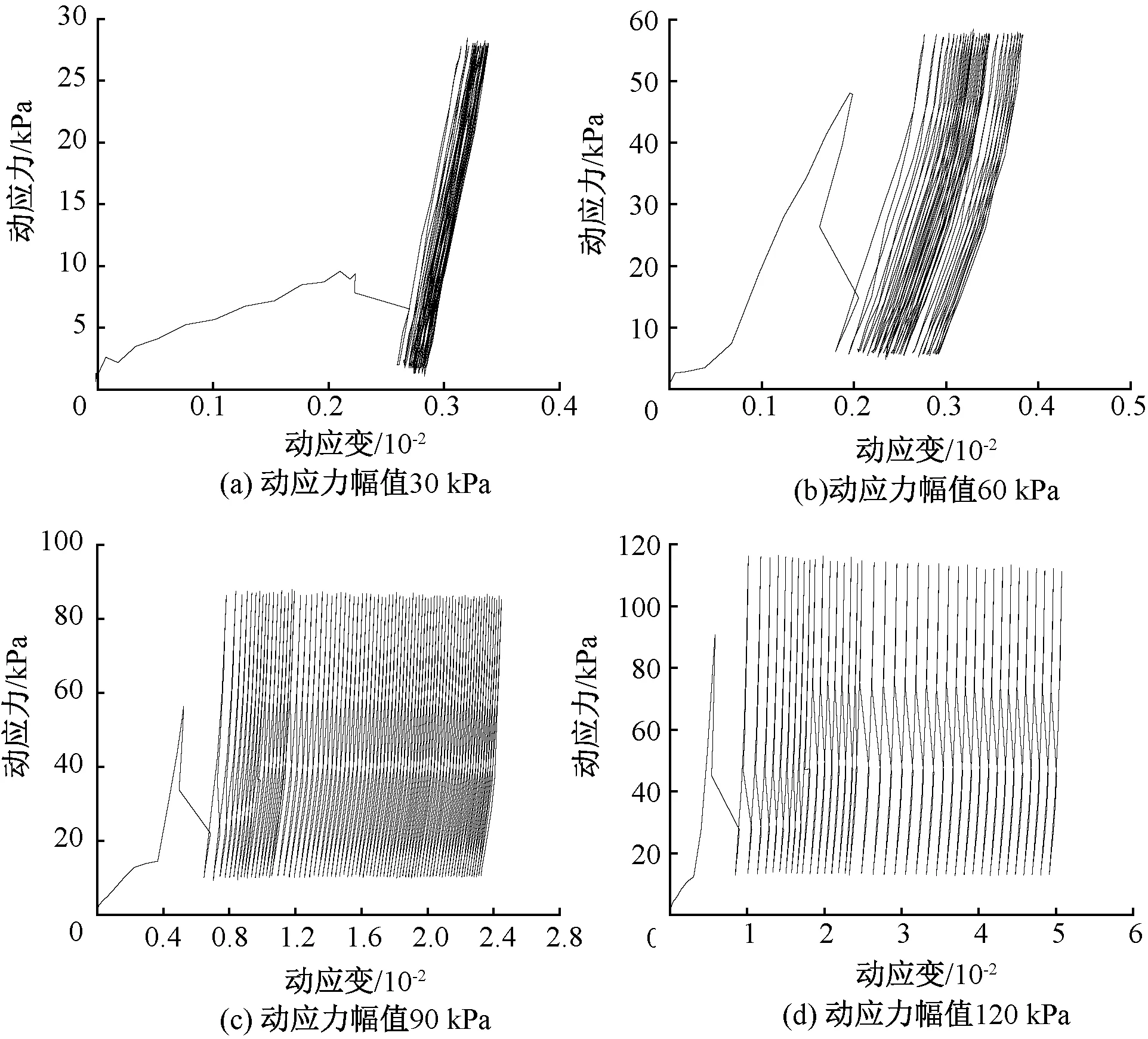
图10 不同动应力幅值下粗粒土的滞回圈曲线

3.3 动弹性模量

动弹性模量是土动力学中最重要的参数之一，等效线性本构模型是对动弹性模量随动应变衰减规律的定量描述。试验中的动荷载具有周期性，使得动应力和动应变之间表现出滞回关系，根据滞回曲线，粗粒土的动弹性模量可计算为

(1)

根据试验结果计算不同细粒含量和含水率条件下粗粒土的动弹性模量Ed。图11列出了动应力幅值为120 kPa，围压为30 kPa，含水率为4%时，不同细粒含量条件下动弹性模量与轴向加载次数之间的关系。图12给出了动应力幅值为120 kPa，围压为30 kPa，细粒含量为10%时，不同含水率条件下动弹性模量与轴向加载次数之间的关系。

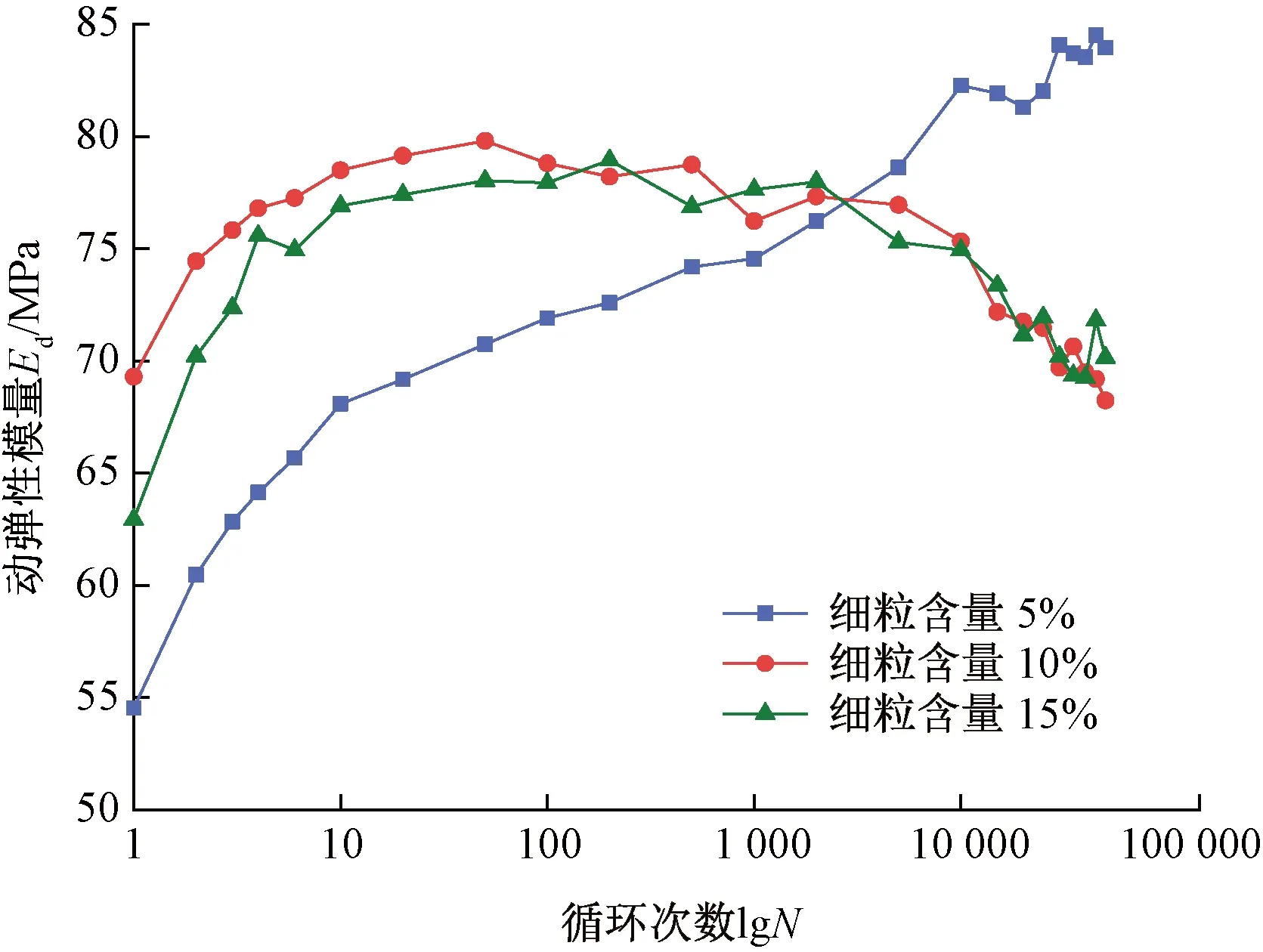
图11 不同细粒含量粗粒土动弹性模量

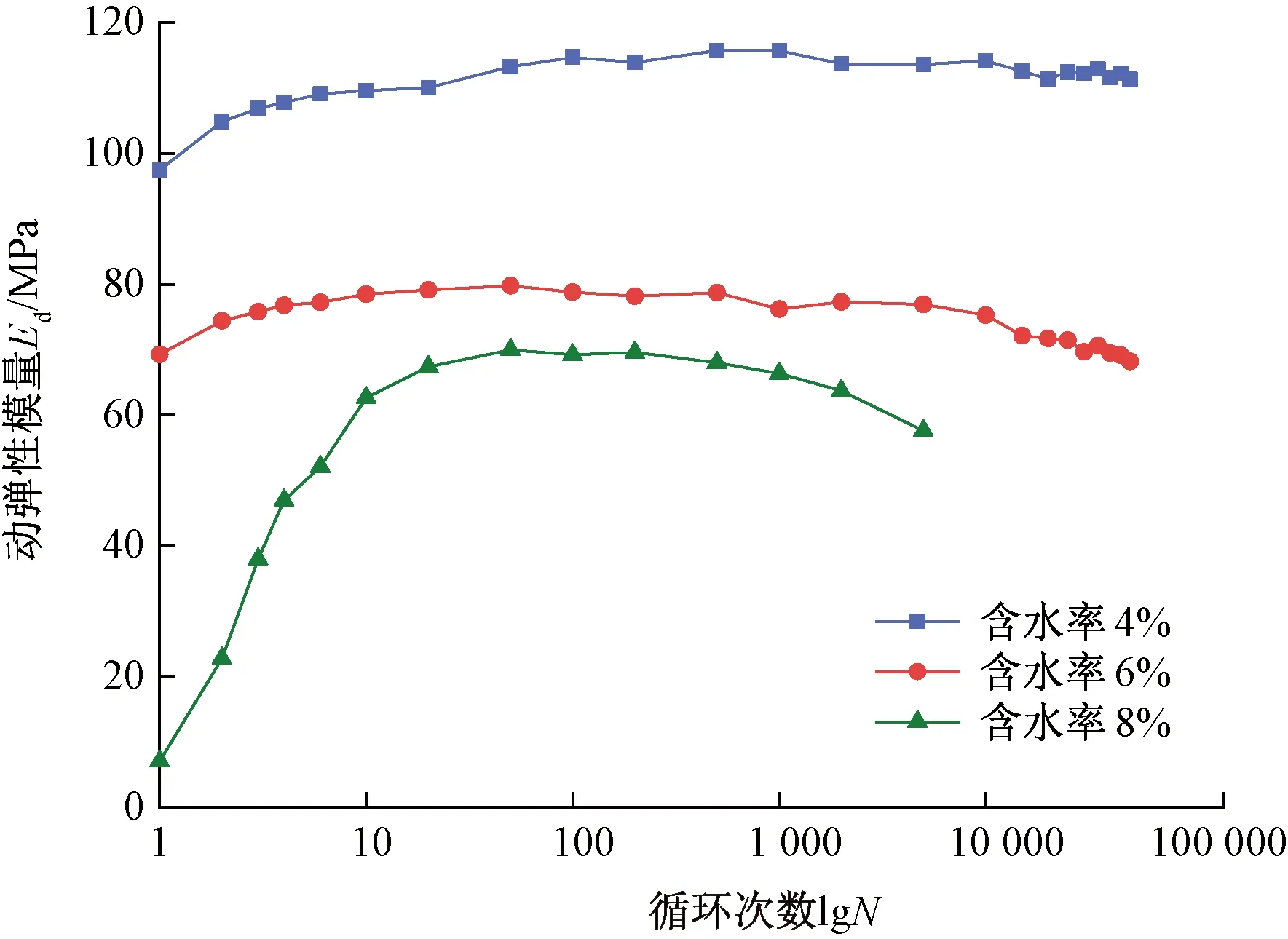
图12 不同含水率粗粒土动弹性模量

从图11可以看出，在前10次加载过程中，粗粒土动弹性模量随着加载次数的增加逐渐增大，细粒含量为10%的粗粒土动弹性模量最大，说明在较低的轴向加载次数下，细粒含量为10%的粗粒土最先被压实，而细粒含量为5%的粗粒土则正好相反。当加载次数为10～100次时，细粒含量为15%和10%的粗粒土动弹性模量增速逐渐减小，细粒含量为5%的粗粒土动弹性模量则继续保持较高的增长速度。

当粗粒土试样加载次数超过100次时，除细粒含量为5%的粗粒土动弹性模量持续增加外，其他两种类型粗粒土动弹性模量均呈现减小的趋势；当加载次数超过1 000次时，细粒含量为5%的粗粒土动弹性模量增长加剧；当加载次数超过5 000次时，细粒含量为5%的粗粒土的动弹性模量已经超过其他两种类型的粗粒土。这主要是由于细粒含量较低的粗粒土在加载初期由于土颗粒间的孔隙较大，导致其变形较大，随着加载次数增加，粗粒土颗粒之间逐渐形成一定的咬合骨架。细颗粒含量较大的粗粒土，加载初期由于细粒土的存在，粗粒土之间的孔隙相对较小，多被细颗粒填充，因此变形也较小，但细粒含量较高，抑制了粗颗粒之间稳定的咬合骨架的形成，导致摩擦力减小。

从图12中可以发现，在前10次加载过程中，含水率为4%的粗粒土动弹性模量最大，最先被压实，更易形成稳定结构；含水率为8%的粗粒土则正好相反，其动弹性模量在加载初期最小，随着加载次数不断增加其增长速率最快。当加载次数达到100次时，三种含水率的粗粒土动弹性模量逐渐趋于稳定，此时含水率为4%的粗粒土动弹性模量最大；当加载次数达到1 000次时，含水率为6%和8%的粗粒土动弹性模量开始减小，且含水率为8%的粗粒土动弹性模量减小速率要明显大于含水率为6%的粗粒土，而含水率为4%的粗粒土动弹性模量基本保持不变。这主要是由于含水率越大，颗粒之间的摩擦力越小，随加载次数的增加，土体的变形持续增大，动弹性模量减小。