基于小波奇异值与SVM 的GNSS 欺骗干扰识别技术*
2022-05-10仇佳吟冯少憧
张 洋,仇佳吟,冯少憧
(天维讯达(上海)通信科技有限公司,上海 200434)
0 引言
卫星导航技术日益成熟,全球卫星导航系统(Global Navigation Satellite System,GNSS)在军用和民用领域得到了广泛应用[1-2]。由于卫星导航系统多采用高轨卫星,导航信号传播链路损耗极大,到达地面信号功率微弱,约-160 dBW。在民用领域中,导航信号体制格式公开,产生了大量以卫星导航技术为基础的无人机管制设备。无人机管制设备使用时会发射卫星导航欺骗干扰信号,导致卫星导航信号受欺骗干扰和管制干扰的问题日益严重[3-4]。例如,伊朗曾利用全球定位系统(Global Positioning System,GPS)欺骗技术俘获美军无人机;设置在上海某机场附近的用于防止无人机越界的无人机管制设备,造成了卫星导航信号偏离实际位置,影响民航飞机起降安全[5];2020 年,上海某油库设置的用于防范无人机恐怖袭击的无人机管制设备,导致上海黄浦江某航道出现了船舶漂移到陆地转圈的现象,影响航运安全[6];美国曾在实验室中依靠GPS 成功控制无人机升降[7]。
对卫星导航欺骗干扰识别的研究已经成为国内外研究的热点,提出了以欺骗信号与真实信号功率差值为基础的信号功率检测技术,通过设定适当的功率检测门限识别欺骗信号。Jafarnia 等人[8]提出了一种解扩前的欺骗信号检测方法,进一步优化了信号功率检测技术,但其受外部电磁环境影响大,误判率较高。基于相关器功能的信号质量检测技术[9]降低了外部电磁环境对识别准确率的影响,但是不适用于大功率欺骗信号场景。张婧等人[10]在传统识别方法的基础上了引入了神经网络算法,分别提出了基于反向传播(Back Propagation,BP)神经网络和基于多项式支持向量机(Support Vector Machine,SVM)的GPS 干扰信号识别方法,对常见的含噪干扰信号具有较高的识别准确率,但是未对相似度较高的欺骗干扰信号做测试验证。2018 年,Yuan 等人[11]通过进行联合检测霍夫曼变换后得到的接收信号的载波多普勒和码多普勒,实现了对真假卫星导航信号的识别,但是复杂度较高。
本文提出了一种基于小波奇异值与SVM 的GNSS 欺骗干扰识别算法。文中第一部分介绍了GNSS 欺骗干扰信号识别原理;第二部分给出了实验与结果分析,分析比较了基于北斗导航系统的欺骗干扰识别技术和基于载噪比与经纬度的欺骗干扰识别技术;最后给出了总结。
1 欺骗干扰信号识别原理
1.1 欺骗干扰信号
GPS 信号分布在中心频率为L1、L2 和L3 的频段上,由载波信号、测距码和导航电文构成,其中测距码包括C/A 码和P 码。由两个10 级线性移位寄存器产生的m序列,经过模二加之后可得到C/A码,寄存器生成序列分别为G1和G2:
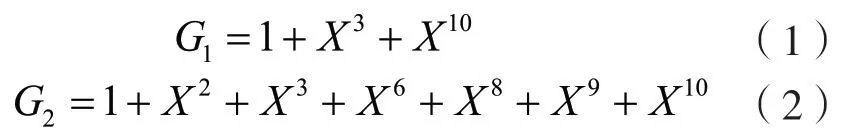
式中:X为二进制数据。
导航电文(数据码)包括卫星星历、卫星时钟改正参数、电离层改正参数等[12]。在L1 频率,比特速率为50 bit/s,每比特持续20 ms。数据码以组帧的方式组成,25 个主帧组成一帧,每个主帧由1 500 bit 组成,持续30 s,5 个子帧组成一个主帧,每个子帧长300 bit,共计6 s。卫星导航欺骗干扰信号与卫星导航信号构成基本一致,仅通过改变数据码,生成欺骗干扰信号,如图1 所示。
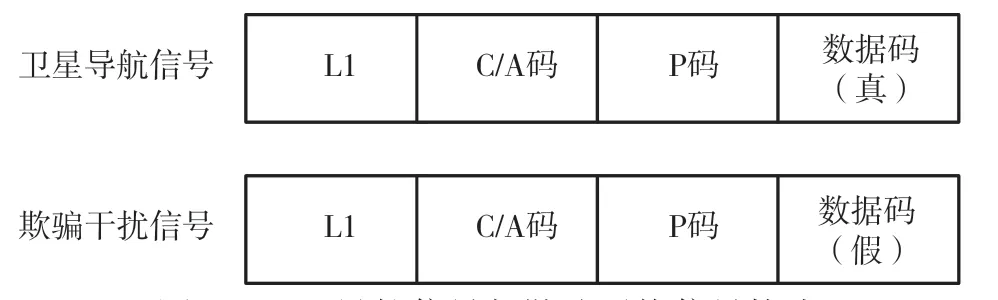
图1 卫星导航信号与欺骗干扰信号构成
1.2 欺骗干扰信号识别原理
基于小波奇异值与SVM 的欺骗干扰信号识别算法将小波变换、奇异值分解与SVM[13-15]相结合,实现准确识别卫星导航欺骗干扰信号的目的。小波变换具有较好的时频分辨特性,能够获得更多的欺骗干扰信号特征。通过滤波器将卫星导航信号f(t)正交投影到空间Vj和Wj,得到尺度j下离散小波变换的低频近似分量和高频细节分量:

式中:n=0,1,…,N-1 为离散时间序列号;j=1,2,…,J为层数;h和g分别为低通、高通滤波系数;A为低频近似分量;D为高频细节分量。
小波分解层数为j时,将真假卫星导航信号分解为近似分量和细节分量,并组成初始特征矩阵(D1,…,Dj,Aj),对该初始矩阵进行奇异值分解处理获得的信号特征,形成样本数据。
引入非线性支持向量机和径向基核函数将低维空间中的非线性可分样本映射到高维空间,形成线性可分样本,此时线性可分样本的最优超平面问题,即几何间隔,达到最大问题可转化为对偶优化问题。通过问题转化,得到最优解ai*,即为支持向量,样本集为{(xi,yi),i=1,2,…,n},xi为样本,yi∈{+1,-1}为类别标号,相应决策函数为:

式中:ai*为支持向量;b*为可通过任意支持向量求得的分类阈值;sgn()为符号函数。
本文以径向基核函数K(xi,xj)作为支持向量机的决策函数,具有精度高、参数少的优势,计算方式为:

式中:γ为自由参数。
2 实验与分析
2.1 预处理
在数据预处理中,根据卫星导航欺骗干扰信号数据码与卫星导航信号数据码不同,仿真卫星导航欺骗干扰信号数据码与卫星导航信号数据码如表1 所示,码长为8,伪随机噪声码(Pseudo Random Noise,PRN)为2。

表1 数据码
数据码的码率和码片宽度分别为50 bit/s、20 ms,由于C/A 码周期为1 ms,即每个数据码包含20 个C/A 码组,数据量较大。因此,本文截取C/A 码组的前10 个码进行仿真,如图2 所示,PRN 为2 时,C/A 码为1110010000。将数据码与C/A 码做异或运算,即扩频调制,如图3 所示。
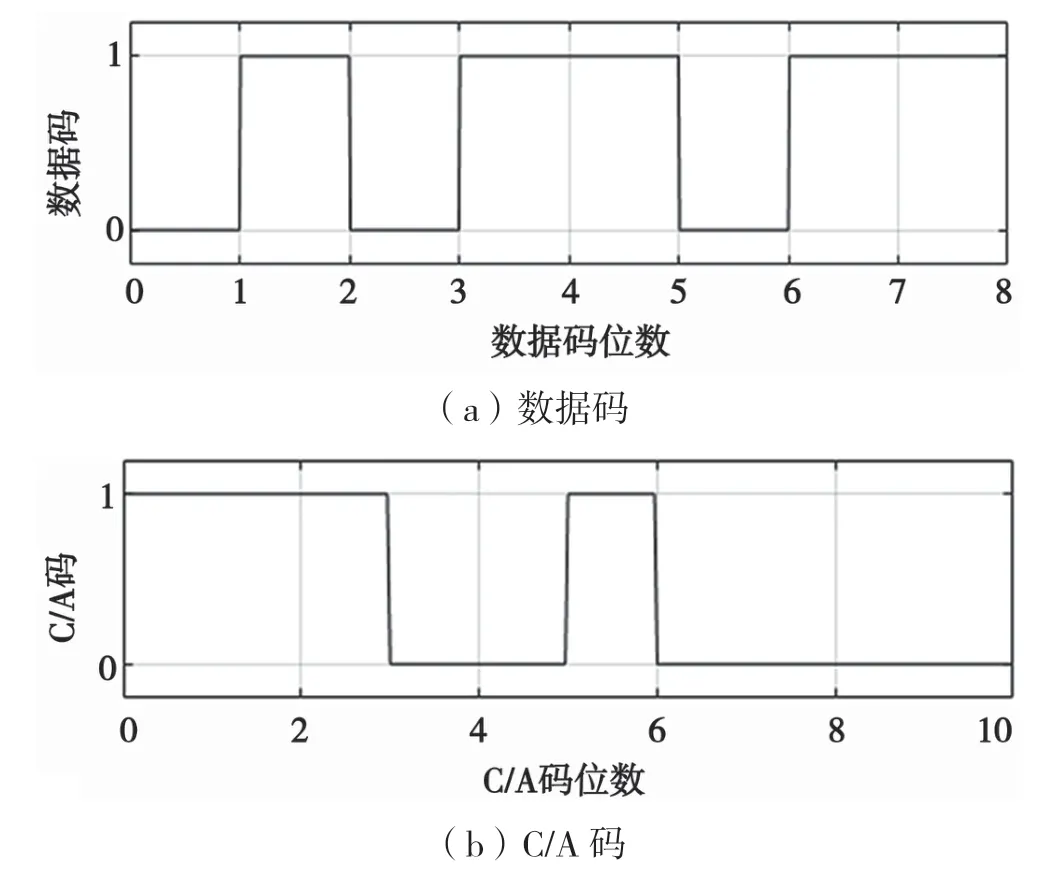
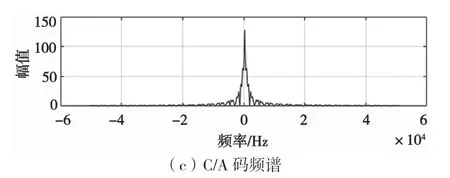
图2 数据码与C/A 码
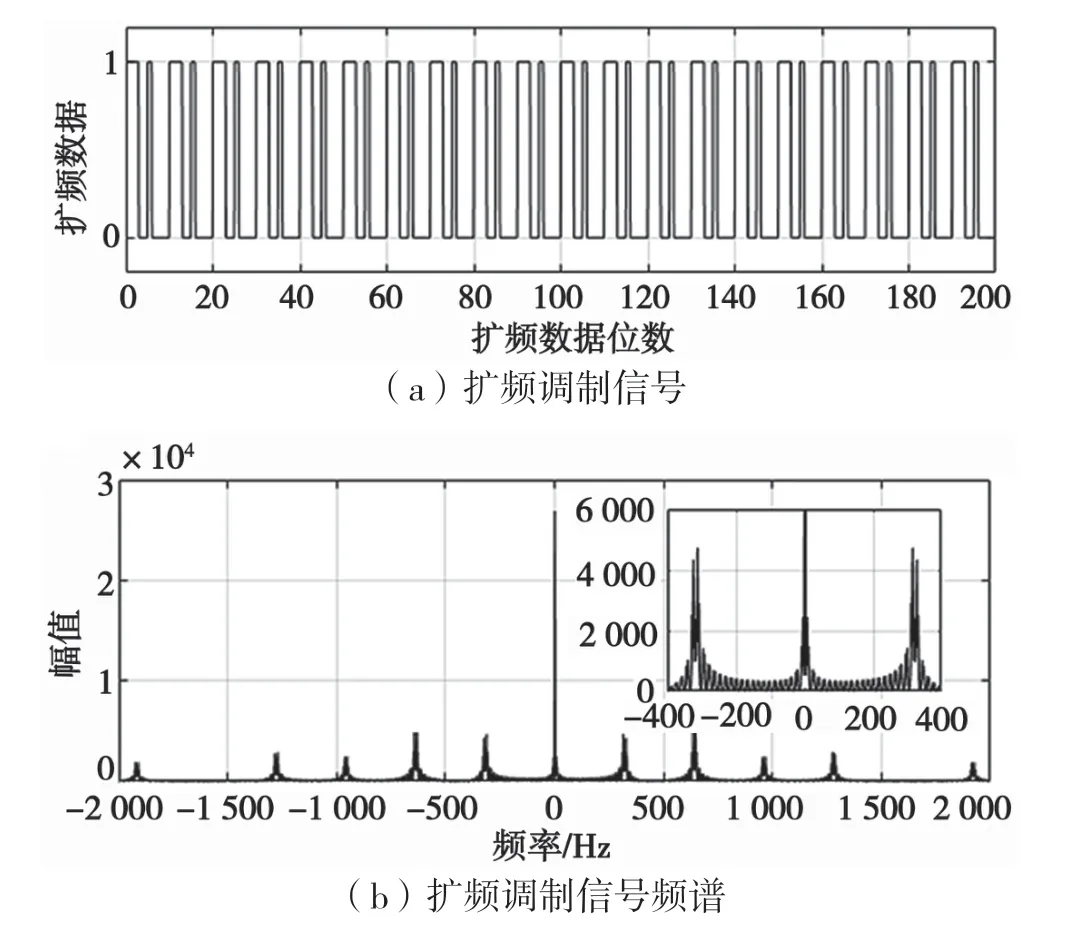
图3 扩频调制
扩频数据需载波调制后经卫星天线发射形成卫星导航信号,最后由地面接收并解调该导航信号。将卫星导航扩频数据、卫星导航欺骗干扰扩频数据分别进行载波调制,调制方式为二进制相移键控(Binary Phase Shift Keying,BPSK)调制,如图4 所示,调制后卫星导航信号与欺骗干扰信号频谱特征基本一致,识别区分难度较大。

图4 卫星导航信号与欺骗干扰信号频谱
2.2 卫星导航欺骗干扰信号分类识别
为了准确区分相似度较高的卫星导航信号与欺骗干扰信号,采用小波变换提取卫星导航信号与欺骗干扰信号频谱特征。小波分解层数为20 层,分别提取低频近似分量与高频细节分量,建立卫星导航信号与欺骗干扰信号高维初始矩阵分别为:

对两组高维初始矩阵做奇异值分解处理,降维得到卫星导航信号与欺骗干扰信号一维特征向量,如图5 所示,两者欧氏距离为2.82,相似度仍较高。
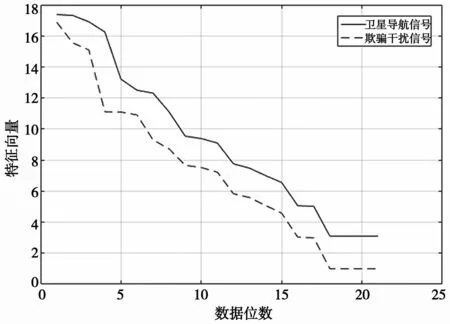
图5 卫星导航信号与欺骗干扰信号特征向量对比
采用非线性支持向量机结合径向基核函数分类处理相似度较高的一维特征向量,对卫星导航信号和欺骗干扰信号进行二分类,构造最优超平面,识别卫星导航欺骗干扰信号,如图6 所示。经过多次测试实验分析,基于小波奇异值与SVM 的GNSS 欺骗干扰识别算法能够准确分类识别卫星导航信号与欺骗干扰信号,识别准确率为90%。

图6 卫星导航信号与欺骗干扰信号分类识别结果
2.3 对比分析
由于北斗导航系统的日益成熟,本文对基于北斗导航系统的欺骗干扰识别技术和基于载噪比与经纬度的欺骗干扰识别技术进行了分析研究。
基于北斗导航系统的欺骗干扰识别技术通过计算其他导航信号与北斗导航信号的经纬度差值,并比较其与已设阈值的关系,识别欺骗干扰信号。识别结果如图7 所示,识别准确率可达95%以上,但是需要严格要求北斗导航信号未被干扰,适用条件苛刻。基于载噪比与经纬度的欺骗干扰识别技术通过载噪比以及经纬度变化识别欺骗干扰信号,大载噪比场景时,识别准确率为95%,小载噪比时,识别准确率较低。GNSS 欺骗干扰信号识别技术对比分析如表2 所示。
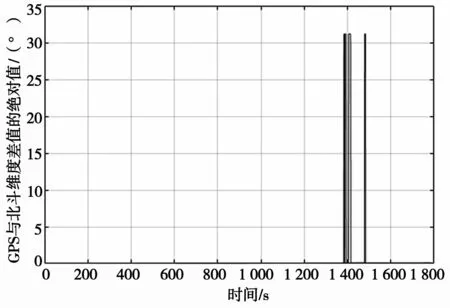
图7 基于北斗导航系统的欺骗干扰识别结果
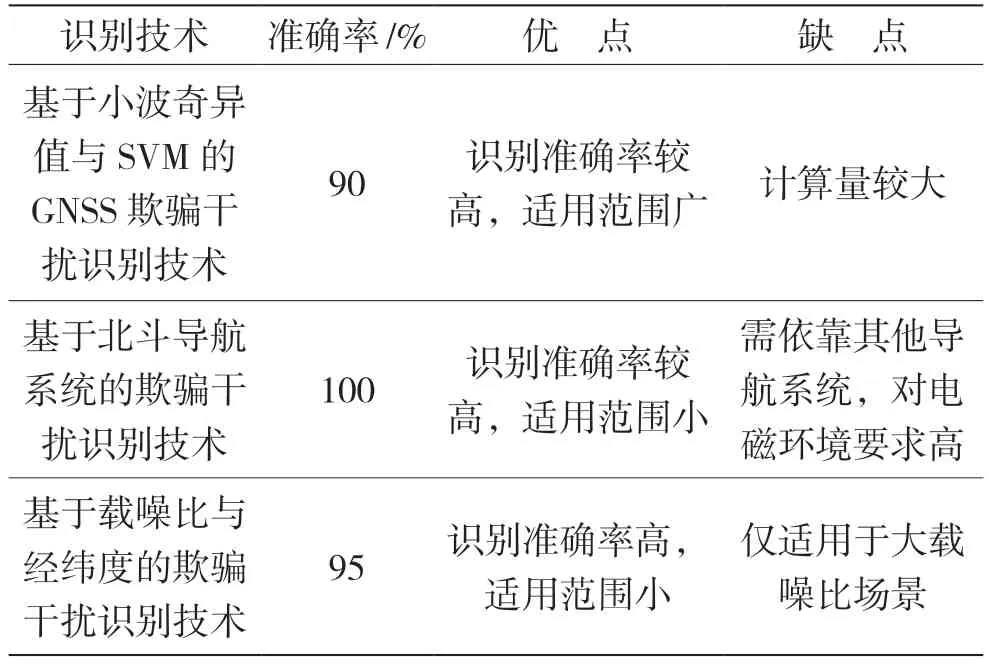
表2 GNSS 欺骗干扰信号识别技术对比分析
3 结语
本文提出了基于小波奇异值与SVM 的GNSS 欺骗干扰信号识别算法,对卫星导航信号和欺骗干扰信号进行了仿真;采用小波变换分别提取了卫星导航信号与欺骗干扰信号特征,形成了高维矩阵;使用奇异值分解对高维矩阵进行了降维处理,分别建立了低维特征向量;结合SVM 建立了最优超平面,实现了卫星导航信号与欺骗干扰信号的分类识别。研究结果表明,基于小波奇异值与SVM 的GNSS 欺骗干扰信号识别技术能够有效识别卫星导航欺骗干扰信号,适用范围广,识别准确率为90%。
