基于迭代网函数插值的椒盐噪声去除算法*
2022-05-10杨陈东曹盼盼杨慧慧项光辉李建飞
杨陈东 曹盼盼 杨慧慧 项光辉 李建飞
(西安航空学院理学院 西安 710077)
1 引言
图像在成像、传输时受到设备、环境等因素影响,容易产生噪声,其中,作为一种十分重要的噪声,椒盐噪声严重影响图像信息获取[1]。传统方法中,均值滤波(Mean Filtering,MF)利用周围像素均值代替噪声点像素,容易造成图像边缘模糊。为此,郭慧娟[2]等提出了一种自适应迭代均值滤波算法(Adaptive Iterative Mean Filtering,AIMF),该算法对噪声点采用多轮迭代去噪,较传统滤波算法有明显优势,特别对去除高密度噪声效果显著。梁利利等[3]将小波变换和均值滤波的优势结合起来,提出基于小波变换和均值滤波的图像去噪方法提高了去噪效果。
另一种典型的方法是中值滤波(Standard Median Filtering,SMF)算法[4],其优点是容易实现、去噪能力强且计算效率高,但是由于其对图像上的像素点粗略地采用邻域中值替代,易导致图像细节损失。因此,多位学者不断对其改进。CHANG等[5]使用阈值和标准中值来检测噪声,并加入了中心加权中值(Center Weighted Median,CWM)滤波器,将噪声像素值改变为更接近或与标准中值相同的新像素值。RIJI等[6]根据高密度噪声去噪效果差的缺陷,提出一种方向加权模糊中值滤波噪声检测与降噪方法,引入模糊梯度值检测噪声,利用邻域像素方向加权中值进行滤波,提高了滤波效果。
近年来,针对椒盐噪声去除的新方法也不断被提出,然而它们多数以增加运算复杂度为代价。Wu等[7]采用全变分(Total Variation,TV)图像修复模型去除椒盐噪声,当噪声密度过大时,也能有效地复原图像,但其计算复杂、时间成本高。黎彪等[8]针对椒盐和高斯白混合噪声,提出一种图像小波去噪的改进阈值函数,比其他阈值函数更加光滑,去噪效果更好。
网函数插值是一种多变元函数插值法,对于网函数空间中的函数,用网函数插值算子可以得到准确值。由于其易于掌握、结构简单以及便于计算机自动划分等特点得到广泛应用,如重力勘探区域场校正、植物群落种群分布格局以及分形插值等[9]。宋莎莎[10]等基于网函数插值的方法,对蝴蝶结效应进行修正,有效避免相关系数方法计算重复行数的不稳定性问题。谭振杰等[11]针对计算机生成图像和拼接图像伪造,提出一种基于网函数插值法的数字图像盲检测算法,该算法具有更高的效率、准确率和稳定性。侯海娜等[12]将网函数插值理论与TV模型结合,提出一种Net-TV算法用于图像修复。杨陈东等[13]将Net-TV算法应用于椒盐噪声去除,过多次迭代达到满意效果。张晰等[14]利用椒盐噪声的奇异点和不相关特性检测椒盐噪声,根据椒盐噪声所在位置,采用网函数插值方法对图像进行恢复和重构,有效去除高密度噪声。
本文基于网函数插值理论结合扩散的思想,构造迭代网函数插值算法去除椒盐噪声。利用典型的椒盐噪声检测算法,将像素点划分为含噪像素点和信号点。在含噪像素点处,利用网函数插值进行多次迭代,使得非噪声点信息逐渐“扩散”到噪声点,完成去噪。
2 迭代网函数插值去噪算法
网函数插值仅使用噪声点的邻域信息,可以在不依赖于邻域相关性的情况下修复噪声区域。如图1所示,矩形D是在直角坐标xO y的平面上的普通矩形,Pi(i=1,2,3,4)为D的四个顶点。过点Q作平行于D的两条平行线与四条边相交于四个点,记作Qj(j=1,2,3,4)(在有些个别的特殊情况下Qj和矩形D的顶点Pi相重合)。矩形D被划分为四个小矩形,面积记作Ai(i=1,2,3,4),D的面积为A(A=A1+A2+A3+A4)。
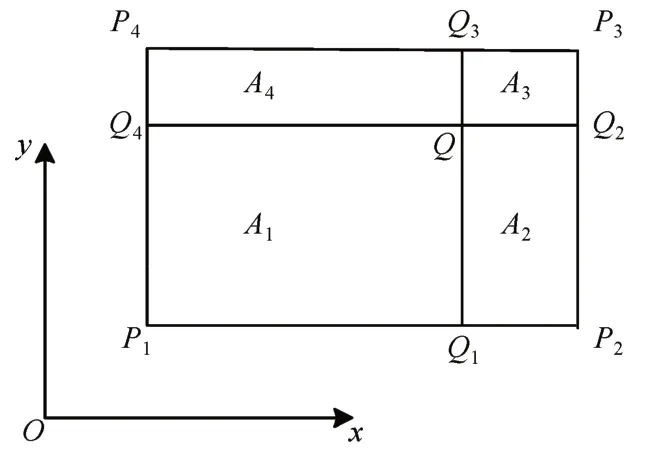
图1 矩形D示意图
记F(Q)为点Q的插值函数值(估计值),使用网函数插值法计算F(Q):

其中,A5=A1。理论证明,对于网函数空间的函数,只需要矩形四条边上的8个点的坐标,便可求出矩形内任意一点的准确值。对于不在网函数插值空间上的其它函数f(x,y),都有式子F(x,y)≈f(x,y),其中(x,y)表示矩形内点Q的坐标。一般而言,矩形的面积越小,F(x,y)与f(x,y)的误差越小。
假设Q是含噪点,D1是图像中某个3×3的正方形窗口,正方形4条边上的每个像素对应于点Q的邻域。如图2所示。那么,将含噪点Q邻域的8个点坐标点及其灰度值带入式(1)中,此时Ai=1(i=1,2,3,4),A=4,则有:
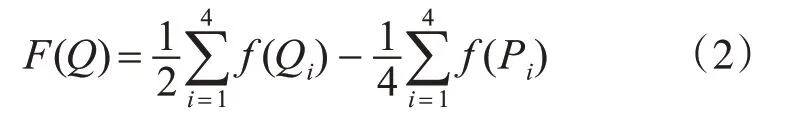
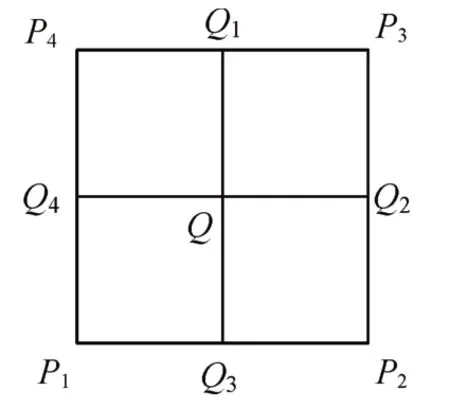
图2 矩形D1示意图
将3×3的窗口滑过整幅图像,即可完成一次去噪。如此循环多次,将修正后噪声点邻域正常像素值信息扩散到噪声点内部,便可提高去噪效果。从式(2)可以直观地看出,使用网函数插值算法计算每个像素点,具有运算简单、容易实现等特点。根据该算法特点,此处将其记作迭代网函数插值去噪算法,算法步骤如下:
步骤1:输入图像。
步骤2:图像延伸。噪声点检测和噪声去除需要邻域的像素值,为避免边界像素点检测不到而影响实验结果,处理图像时首先对图像进行延伸,即把四个边界值向各方向复制1个单位;
步骤3:噪声检测。采用文献[15]中椒盐噪声检测算法,当传入一幅图像,每个像素点以自身为中心的3×3的窗口,在图像自上而下、自左向右地滑动一次,将“salt”和“pepper”标记出来,生成掩膜Mask。
步骤4:噪声去除。根据步骤3生成的掩膜Mask,3×3的窗口自上而下、自左向右地滑动一次,对噪声点进行网函数插值。
步骤5:终止条件。如果满足终止条件,则执行步骤6,否则执行步骤4。终止条件可以根据具体情况设置,此处为了简单且说明问题,设置最大迭代次数T,如果当前迭代次数K>T时,满足终止条件。
步骤6:恢复边界。将延伸后图像还原为原始尺寸。
步骤7:输出图像。
3 实验结果及分析
在Windows10操作系统、8G内存、Intel i51.60GHz,Matlab2016(b)开发环境下,选用Lena图像、Cameraman图像以及House图像(如图3)进行实验,实验的图像均为8位整型、256级灰度,大小为256×256像素,随机添加密度为10%、30%、50%和70%的椒盐噪声。为验证算法性能,分别将本文算法结果与其余文献算法进行对比,并引入峰值信噪比(Peak Signal to Noise Ratio,PSNR)作为图像恢复效果的客观评价标准,PSNR越大,说明结果与原图像越接近,图像恢复质量越高。

图3 实验原图
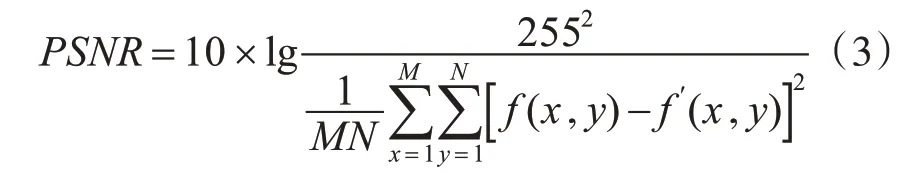
其中,f(x,y)为坐标(x,y)处的图像灰度值,f′(x,y)为去噪后坐标(x,y)处的图像灰度值。
3.1 有效性
添加密度分别为10%、30%、50%和70%随机椒盐噪声的Lena、Cameraman和House噪声图如图4所示。利用本文算法去噪效果如图5所示。

图4 加入不同噪声密度的噪声图

图5 不同噪声密度图像去噪效果图
从图5可以看出,包含不同密度的三种不同噪声图像,利用本文算法均能达到满意直观视觉效果。这表明,迭代网函数插值去噪算法能够有效去除低、中、高不同噪声密度椒盐噪声。
为进一步验证算法有效性,选取Lena图在50%密度噪声下,与不同文献去噪结果进行对比结果如图6所示,不同文献PSNR值如表1所示。
图6中,针对50%密度噪声,均值滤波(MF)与中值滤波(SMF)已经不能去除椒盐噪声,结果图中仍然存在明显的噪声。文献[5]、文献[6]和文献[8]虽然去除了椒盐噪声,但是导致图像边缘模糊。从结果图可以看出,本文算法能够去除椒盐噪声的同时,有效保持图像边缘细节。表1中,本文算法客观评价指标PSNR也高于其他对比文献,说明本文算法使得图像恢复质量更高,可以有效去除椒盐噪声并达到较好效果。


图6 各算法对噪声密度为50%的Lena图恢复效果比较

表1 各算法去噪后图像的PSNR/dB
3.2 收敛性和高效性
收敛性是迭代算法持续得到可靠、稳定结果的前提,然而并不是所有算法在持续迭代过程均能保持收敛。为验证本文算法的收敛性,图7展示了本文算法在不同噪声密度条件下,对Lena图像去噪过程中PSNR值的变化过程。表2列举出本文算法对不用密度噪声Lena图,不同迭代次数时PSNR数值。如表2所示,网函数插值迭代1次能够是图像质量有较大提升,这在文献[14]中也得到验证。更重要地,随着迭代次数增加,PSNR值能够不断提升,最终达到稳定。当噪声密度达到70%,随着去噪难度的增加,相应的迭代次数也随之增加,最终收敛于满意效果。这说明,本文算法能够保持良好收敛性。
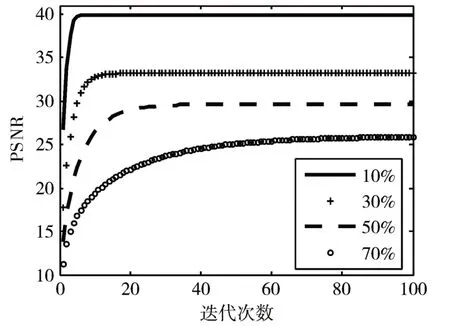
图7 不同噪声密度下本文算法迭代次数和PSNR的关系图
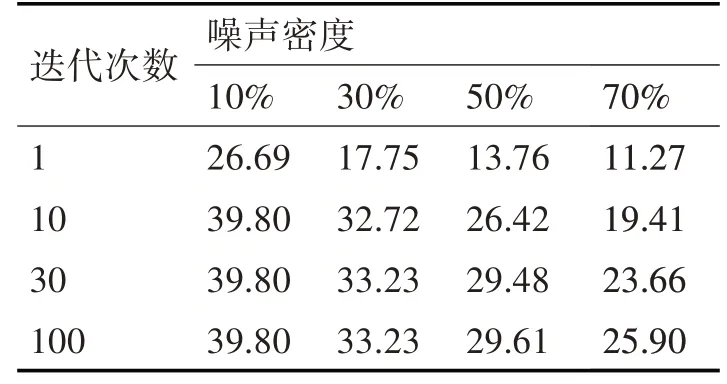
表2 本文算法不同迭代次数下Lena图PSNR/dB
为验证本文算法的运行效率,选取Lena图在不同噪声密度(10%、30%和50%)下,各算法运行时间进行对比。图7表明,含噪密度10%、30%的图像迭代10次时去噪效果趋于稳定,含噪密度50%的图像迭代30次去噪效果趋于稳定,因此实验中分别设置T为10、10、30次,结果如表3所示。可以观察到,含噪密度为10%和30%情况下,本文算法效率远高于其他算法,这主要由于其10次迭代就能趋于稳定状态。含噪密度50%的图像修复时间稍长,但是仍在可接受的范围内。显然,在去噪难度提升时,合理牺牲运行时间来保证去噪效果不可谓不明智的选择。事实上,从式(2)中可以得知,完成一次网函数插值只需要2次乘法运算和7次加法运算,这说明网函数插值十分高效,这无疑决定性地保证了本文算法具有较高效率。
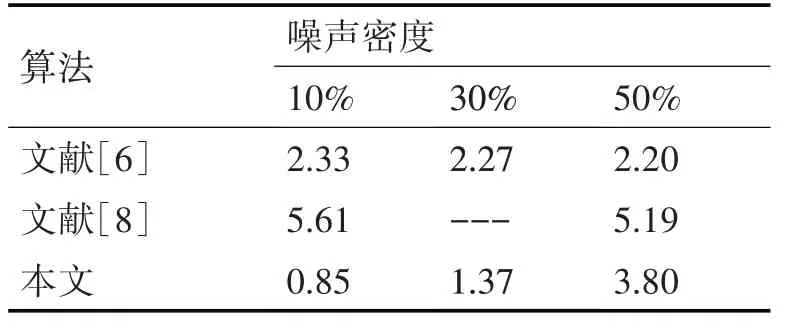
表3 各种算法处理含噪图像运行时间(单位:s)
4 结语
一种运算简单且有效去除椒盐噪声的图像去噪算法被提出。此算法利用网函数插值多次迭代去除噪声点:1)保持了高效的运算效率;2)多次迭代使得高密度噪声点被不断修正,去噪图像能够不断接近真实图像,取得良好去噪效果和收敛性;3)针对低、中、高不同水平椒盐噪声,该算法均有较好去噪效果,且能保护图像边缘信息。
