融入动态技能学习时间分类的知识追踪模型*
2022-05-10许晓东
宋 刚 许晓东
(江苏大学计算机科学与通信工程学院 镇江 212000)
1 引言
ITS是一个活跃的研究领域,旨在为学生提供个性化的指导。早期工作可追溯到20世纪70年代后期,在各种各样的人工智能和知识表示技术中,主要有基于规则和贝叶斯的学生知识和误解的表示,项目响应理论中逻辑回归的技能建模,强化学习和深度学习[1]。在知识追踪问题上,我们无法将学生的知识状态是定义为静态的,而且学生对每个知识点的掌握情况并不是独立的[2],DKT采用的是循环神经网络(RNN),它相对于著名的贝叶斯知识跟踪模型(BKT)取得了显著改善,其结果已被证明能够发现技能概念中的潜在结构,可用于课程优化[3]。但是忽略学生实际答题时间带来的个体化差异问题,会影响模型训练的准确度。
针对上述问题,本文将学生当前的答题时间编码,结合答题情况输入模型,结合改进的损失函数,来预测学生的表现。
2 相关工作
我们在这里回顾四种最先进的学生建模方法,用于评估学生的表现,无论是他们在心理计量学(IRT)或教育数据挖掘(BKT)中的优势,还是因为他们是表现最好的(PFA,DKT)。参见文献[4]进行一般性回顾。
2.1 基于项目反应理论的模型(Item Response Theory,IRT)
IRT假设学生的知识状态是静态的,并且在测试期间完成评估时以其熟练程度表示[5~8]。IRT为单个技能建模,并假定测试项目是一维的。它为学生i分配了静态熟练度θi。每个项目j都有自己的难度βi。IRT的主要思想是通过使用学生的能力和项目难度来估计学生i正确回答项目j的可能性。
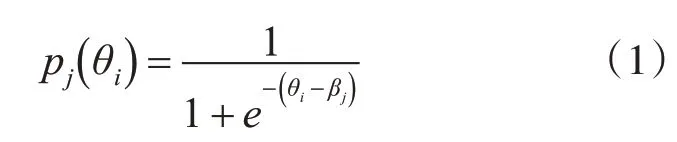
2.2 贝叶斯的知识追踪模型(Bayesian Knowledge Tracing,BKT)
贝叶斯知识追踪(BKT)模型[9]是一个将学生知识点掌握情况表示成一个二元变量,其中学生的表现是观察到的变量,学生的知识是潜在数据。该模型采用学生的表现,并使用它们来估计学生对特定技能的知识水平。引入BKT是为了在学习环境中进行知识跟踪,对于该学习环境,静态知识状态的假设已被丢弃。用以下4个概率不断更新学生对技能知识的标准BKT估计:[P(L0)掌握的初始概率,P(T)从未掌握转变为精通,P(G)猜测和P(S)滑移]。
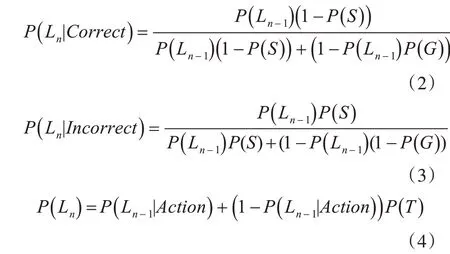
2.3 绩效因素分析(Performance Factor Analysis,PFA)
PFA是BKT的替代方案,它还放宽了静态知识假设,并以其基本结构同时为多种技能建模[11]。它定义学生i成功完成项目j的概率为
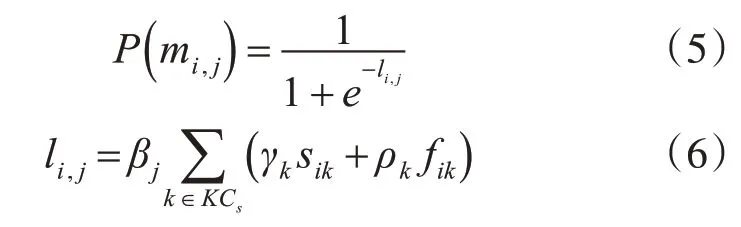
其中βk是技能k的偏差,而γk和ρk分别代表技能k每次成功和失败尝试的学习收益。sik是成功尝试的次数,而fik是学生i对技能k的失败尝试的次数。
2.4 深度知识点追踪(DKT)
DKT是在[3]中引入的。它使用长短期记忆(LSTM)[12]动态地表示学生的潜在知识空间。可以通过利用学生历史表现来推断学生通过习题增加的知识。DKT使用大量的人工神经元来表示潜在知识状态以及时间动态结构,并允许模型从数据中学习潜在知识状态。它由以下等式定义:

在DKT中,tanh和sigmoid函数均按元素种类应用,并通过输入权重矩阵Whx,循环权重矩阵Whh,初始状态h0和输出权重矩阵Wyh进行参数化。隐藏和输出单元偏置量用bh和by表示。
3 深度知识追踪
3.1 学生的学习时间分组评估
在教育领域[13~14]的几项研究工作中,根据他们先前在学习系统中各种内容上的表现,将学生分为具有相似学习能力的不同群体,以向具有相似学习能力的每组学生提供更多的适应性指导。目前大多数的网上学习平台,在缺少线下老师的管理情况下,学生的自制力低,追踪学生的学习状态,可以对学生的学习情况进行更准确的预测。在每个时间间隔对学生的学习情况动态评估,是根据下一个时间间隔开始之前,对他们处理知识点的时间进行聚类进行的。
1)时间间隔:时间间隔是一个段,是学生尝试回答系统中同一知识点的时间差。从这个角度来看,一个时间点(时间戳)是对知识点的一次尝试。
2)划分学生的尝试序列,将每个学生的响应序列划分为多个时间间隔有两个目的。
(1)减少计算量和内存空间分配,以便在整个较长的序列中进行学习。(2)在每个时间间隔后重新评估学生的学习状态,并在下一个时间间隔中将其动态分配到所属的组中。
图1举例说明一个学生的16次尝试响应序列,其中技能标签13进行了5次尝试,分为4个片段(时间间隔)的示例,其中一个片段代表一个时间间隔,在该时间间隔中,学生尝试的次数根据他们与系统交互过程中回答的问题数量而有所不同。
3)用于聚类的长期状态编码:根据学生技能学习的时间对学生的学习时间进行分组,可以从数据集D中获取,学习时间分类的配置文件被编码为具有技能数量长度的向量。获取学生当前技能的时间戳与先前尝试的该技能的时间戳之间的差值,在时间间隔内对学生i进行聚类,如下所示:

其中Timestamps(xj)1:z代表学生i对n个技能(x1,x2,…,xn)的从开始答题到当前答题的时间,表R(xj)1:z表示在1到z次的时间间隔内,对技能j最近一次的回答时间差,而表示一个向量,其中包含学生i对每种技能的学习次数概括,学习次数1到z。每个学生在与系统交互的生命周期中同一技能的学习可能会有不同数量的总学习次数。
4)K-means聚类:通过在数据D上进行聚类[15~16],聚类训练阶段,在不考虑学习次数的情况下找到每个学生组的质心。一旦计算出,在整个聚类过程中,每个组的质心将不再改变。将每次技能的学习状态(在训练和测试数据中)分为不同的组,其中1代表学习状态最差,递推,4代表当前学习状态最佳(参见图2)。

图2 技能学习的时间间隔对学生进行聚类
找到学生i学习技能所属的组,使用学习状态配置数据点在学习了所有K个聚类的质心之后,每个学生每次技能的学习状态Se gz都通过以下方程式分配到最近的聚类Cc中:
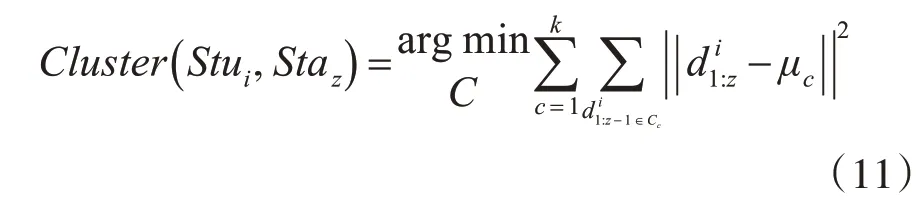
其中,μc是学生组去除极端情况下聚类集Cc(k均值聚类中C2,…,Ck-1)中点的平均值,状态描述数据表示学生i从学习技能次数从z-1到z的学习时间。
图3是5位学生对相同技能学习时间间隔的表示,是基于他们以前技能答题的时间间隔。答题数量的不同,时间间隔的总数也有差异,其中t1,t2,t3,t4代表学生对同一技能答题时间的时间间隔,t1代表的是学生第二次与第一次对该技能的答题时间差,依次,t2,t3,t4也是代表当前答题时间与上一次答题时间的时间差(其中线条越长代表时间间隔越长)。每次练习的时间间隔(t1,…,t4)都会根据当前技能的第几次练习z,均使用先前的表现数据通过k-means聚类方法进行分配。

图3 学习交互过程中,学生技能学习的时间间隔
3.2 训练目标
在标准DKT中,xt是学生互动元组xt={st,at}的单次编码矢量,它表示st所练习的技能的组合,并且在其中指示答案是否正确。但是学生的学习状态还需要另外加上ct+1,这是一个表示St ui在当前时间间隔技能st的学习状态,是从学生下次的答题时间获取的。在隐藏层中,当我们将响应序列的每个时间间隔的最后一个节点将用作下一个时间间隔的第一节点h0。输出yt是一个与问题数量相同长度的向量。
图4说明了如何通过在每次答题时,将学生的学习状态作为不同的小组信息纳入到DKT模型中来进行改进,以改进知识跟踪中的个性化。因此,可以结合学生下次的答题时间结合当前技能的答题情况获得下次答题正确的概率。为了在模型训练中验证这一假设,我们引入以下损失函数并将其最小化:

图4 在学生与系统的整个交互过程中,每次答题都与一个不同的组(集群)相关联
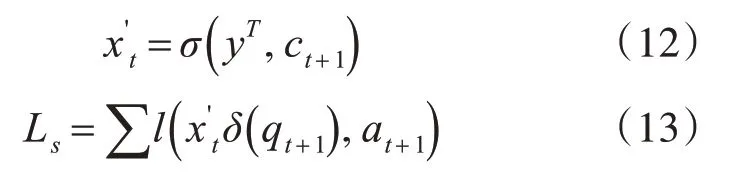
其中是加入学生当前学习情况的单次编码矢量,δ(qt)是技能在t时刻的one-hot编码,at+1是技能回答正确或错误(1或0)的编码,l是二元交叉熵函数。
在这方面,式(7)和(8)对于本文模型仍然有效,本文模型和DKT的输出yt相同,这为特定问题提供了预测的概率。输入层中每次学生答题的时间间隔的颜色表示学生根据其学习状态在该次答题中所属的组。通过添加该学生所属组的聚类信息Cl ust er(Stui,Staz),我们确保这些高水平统计信息仍可用于模型,从而在整个学年中进行预测。DKT模型就是这样做的,以相同的方式对待所有学生,而不考虑他们由于线上学习时间的差异性。相反,通过对学生的学习状态使用聚类,通过在不同的答题时间使用他们的实际学习概况数据来找到一群具有相似学习状态的学生。在每个不同的组中追踪学生的知识可以在学生的成绩预测中提供更大的效果。训练目标是在模型下最大程度地减少观察到的学生反应序列的交叉熵损失函数:

损失函数L'由式(15)定义,并且模型经过优化以最小化此损失函数,其中λ是任意非负实数。最后,我们在表1中总结了每种模型的特征。

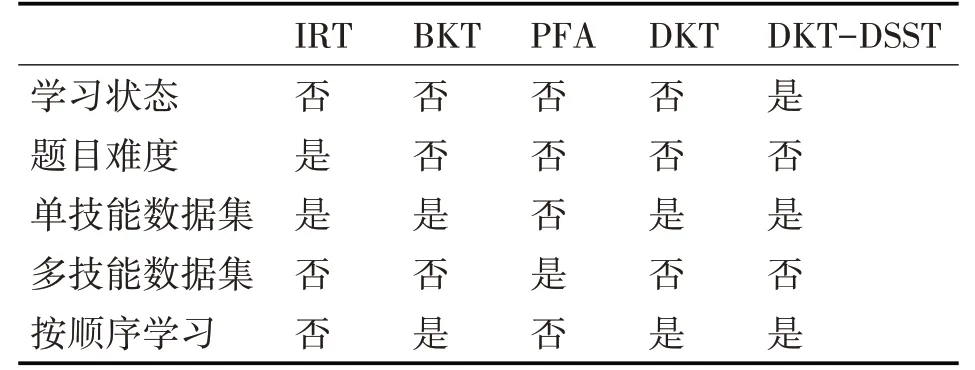
表1 不同模型对比
4 实验
4.1 实验环境及参数设定
本文使用Google的TensorFlow框架实施DKT算法来完成深度知识跟踪的实验。在实验中,我们按照学生的答题序列,将每个数据集随机分为80%的训练数据和20%的测试数据。使用EM训练BKT,并将迭代极限设置为200。DKT中RNN的权重是从具有零均值和小方差的高斯分布中随机初始化的。我们遵循文献[3]中的超参数设置,以0.01的学习率训练模型,训练迭代次数设为100。状态大小为200的单层RNN-LSTM被用作DKT模型的基础,同时也应用了Dropout以避免过度拟合[18],此外,我们还将标准梯度阈值始终设置为3.0。为了加快训练过程,使用了小批量随机梯度下降来最小化损失函数。我们对正则化参数λ执行超参数搜索。首先,根据LARS-EN[19]算法,来有效地计算弹性网络正则化路径,分别检查每个参数以识别给出良好结果的值范围。λ的初始搜索范围为{0、0.001、0.01、0.1、1.0、10.0}。在缩小每个参数的范围之后,对λ的组合进行网格搜索{0、0.25、0.5、1.0}。
4.2 评估方法
为了更好地解释模型的不同方面,文中使用AUC和r2结合使用作为评估指标,为我们提供评估模型的基础。
5 数据集
为了验证模型,我们在两个不同的辅导场景中的三个公共数据集上对其进行了测试,在该场景中,学生与教育环境中基于计算机的学习系统进行了交互。KDD Cup 2010明确的记录了学生开始的答题时间,ASSISTments中没有虽然没有明确标出,在数据集说明中发现了学生的答题时间是包含在log_id中的,数据集信息如表2。
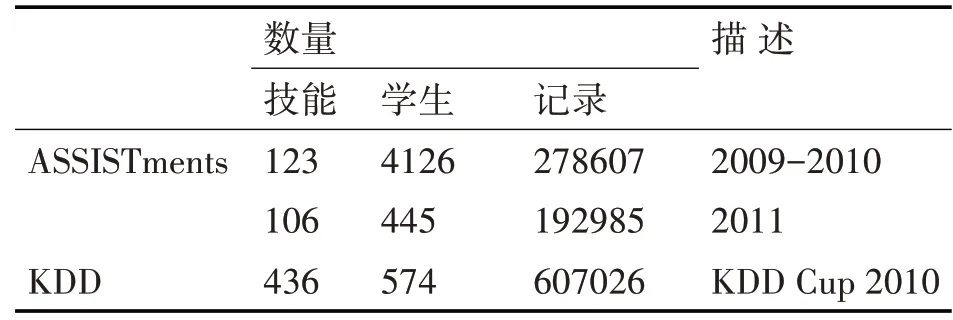
表2 数据集概述
6 实验研究
本文对学生状态的评估来提高预测结果,是对原始DKT算法的扩展,并与具有欧几里得距离的k均值聚类方法结合在一起。我们将所有模型进行比较:IRT[5],BKT[10],PFA[11],DKT[3]。但是,我们无法将其与其他变体模型进行比较,因为它们或多或少相似并且在性能上没有显着差异。对于IRT,我们使用Knewton[5]中的代码,而DKT的代码则来自WPI[17]。将每个模型做出的学生表现预测制成表格,并根据曲线下面积(AUC)和皮尔逊相关系数的平方(r2)评估准确性。
在表3中,本文模型的预测效果在所有数据集中的表现均优于最新模型。在ASSISTments09数据集上,与AUC为0.73的标准DKT相比,我们的DKT-DSST模型实现了0.81的AUC,这意味着10%的显着增长。在ASSISTments11数据集上,结果显示增加了5%,DKT-DSST中的AUC为0.83,而原始DKT中的AUC为0.79。在KDD数据集中,DKT-DSST在AUC=0.79的情况下相比原始DKT也实现了约2.5%的增益。在上述所有模型中,只有IRT模型需要学习问题难度,而所有其他模型仅依赖技能。在表4中,当我们比较r2模型时,BKT在ASSISTments09中为0.07,在ASSISTments11中为0.06,在KDD中为0.05。本文模型在所有数据集中的r2结果均高于0.21。
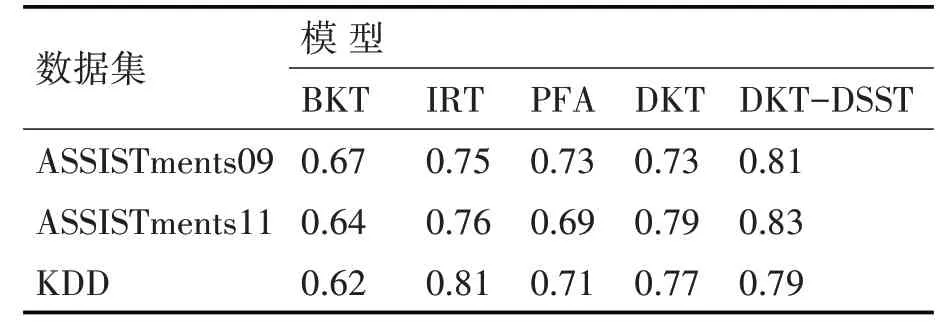
表3 AUC结果
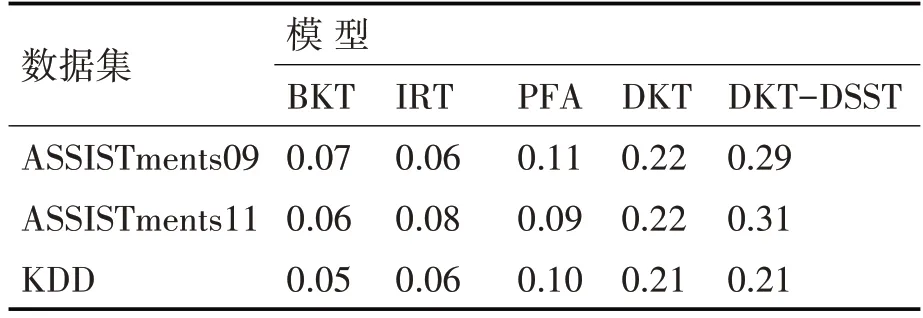
表4 r2结果
表5中我们发现通过融入了学生的学习时间,对模型训练效果只产生了正收益。我们对正则化参数λ执行超参数搜索。首先,根据后面将要说明的一些评估措施,对参数λ给出良好结果的值范围{0,0.25,0.5,1.0},在缩小每个参数的范围之后。对群集的各种划分还提供不同的性能,如表5所述。根据实验结果,将学生学习状态划分为6个群集,参数值为0.25时是本文模型的最佳参数。
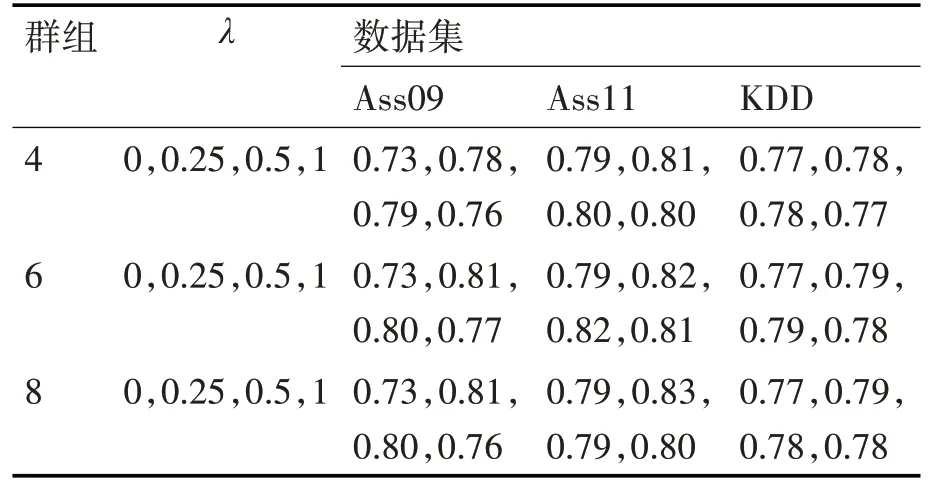
表5 AUC在不同分组下的实验结果
7 结语
本文提出将习题答题时间融入到传统的DKT模型中,并结合改进的模型损失函数,通过AUC与r2证明模型的准确度更强,达到改进目的。
