基于密度峰值优化K-means聚类算法的微博舆情分析*
2022-05-10叶瑾玫
叶瑾玫 程 科
(江苏科技大学计算机学院 镇江 212003)
1 引言
随着互联网的高速发展,互联网已经成为了人们工作和生活中非常重要的一部分。同时,互联网上的信息量也在不断的增长,甚至出现了信息的“大爆炸”。当今的互联网包含着各种各样的信息,网络舆情(Public Opinion)是其中非常重要的一种。
特别是微博的兴起,对企业网络舆情以及社会事件的发展趋势产生着巨大的影响力,作为互联网中的一种新媒体[1],企业将其运用到营销活动、产品或其他企业信息发布等管理活动中,同时也能够让消费者随时随地收听企业微博“直播”,对促进社会的经济建设具有极其重要的意义。
聚类分析是基于相似性的思想,指将相似度较高的数据对象划分为同一类簇,不同类别之间相似度较低的分析过程,通常又被称为无监督学习[2],与监督学习不同的是,在群集中没有指示数据类型的分类或者分组信息。现阶段的聚类算法中,最常用的有一下几种[3]:基于密度的聚类、基于网格的聚类、基于层次的聚类、基于划分的聚类。
K-means作为一种最经典、使用场景最广泛的一种基于划分的聚类算法[4],主要用于网络舆情的聚类分析。然而,该算法存在一些缺陷,随机选取的k个聚类中心点导致结果有很大的随机性,聚类结果很大程度上取决于一开始选取的位置,不能保证全局最优。针对上述情况,研究者围绕K-means算法展开了各种研究,加以改进算法缺点。文献[5]提出基于直方图方法从空间上划分样本数据,凭借数据分散布局具有本身一定的特色来找出初始类簇中心;文献[6]提出依据每个样本对象与类中心点的距离与之轮廓系数自适应地选择高质量样本来确定初始聚类中心;文献[7]生成样本的初始中心是利用密度敏感的相似性度量计算出对象的密度,该中心的生成具有启发性,以均衡化函数为基则确定K值。本文根据每个数据对象的密度分布来选择峰值密度较高的对象作为初始类中心点,并以初始中心数来确定类别数,使用选定的初始聚类中心进行聚类,提高数据分析的准确性、快速性,弥补了K-means算法选择初始聚类中心和类别数目的缺陷,且使得算法迭代次数大大减少。
2 改进的FSDPC算法
2.1 FSDPC算法
FSDPC算法是由Alex Rodriguez和Alessandro Laio于2014年提出,并将论文《Clustering by fast search and find ofdensity peaks》发 表 在Science[8]上。主要思想是寻找被低密度区域分离的高密度区域,类簇中心点的密度大于周围邻居点的密度并且类簇中心点与更高密度点之间的距离相对较大。因此,FSDPC算法主要有两个需要计算的量:局部密度ρi和相对最小距离δi(与局部密度更大的样本点之间的最小距离)[9]。这两个量都与点之间的距离dij相关。对于点的局部密度ρi定义方式有两种:

dij表示两点i和j之间的欧式距离,dc>0为截断距离,每个数据点与之距离不超过dc的点数目大概占数据点总数的2%。
δi与比自己局部密度更高的点的距离定义为
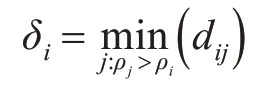
δi是具有最高局部密度的点与所有其他点之间的距离的最大值。定义为

计算出各点的ρi和δi值后,根据ρi和δi值生成决策图,如图1所示。
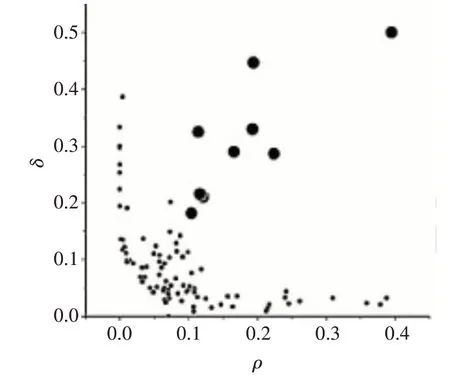
图1 决策图
从决策图中可以选出具有较大局部密度ρi值和较大距离δi值,γi=ρi*δi,γi按从大到小进行排序,γi的值越大则数据点越有可能为聚类中心[10]。
2.2 改进的FSDPC算法
在上述局部密度的计算公式中,截断距离dc参数需要手动设置这一缺陷直接影响了初始中心选取结果,即使将阈值定为选取数据对象的2%,但该算法的鲁棒性依然较弱,本文介绍基于相邻元素最大差值dc选取法。
计算出数据对象间的欧氏距离按升序进行排序,获取到距离集合di={di1,di2,…,din}(i=1,2,…,n),由图2可以看出,在同一个簇中数据点到数据对象i的距离较小,而另一个簇中的数据点到i的距离差距较大,这时距离集合可以设为di={di1,di2,…,dij,di(j+1),…,din}(j=1,2,…,n;i≠j),其中,dij=M,di(j+1)=L。M和L两个相邻的元素之间有着最大差值,则理想的截断距离dci可以定义为

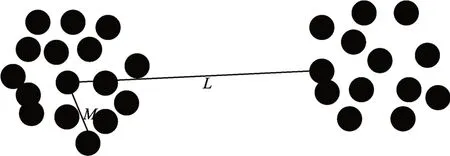
图2 截断距离示意图
对于离群点,从图3中可以看出离群点与簇内数据点同样有着最大差值,即dij=M,di(j+1)=N,则理想的截断距离为
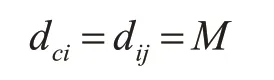
将各个数据对象的截断距离组成集合D={dc1,dc2,…,dcn},该集合中包含有数据群临界点以及孤立点的截断距离,为避免受到这些噪声点的影响,dc应取集合D中拥有最小截断距离的数据对象值,即dc=min(D)。
3 改进的k-means算法
3.1 K-means算法
K-means算法的思想很简单,把给定的样本集按照样本之间的距离大小划分开来,取k个类簇和k个初始中心,将数据样本点分配到与之距离最近的类簇中,以保证各簇中数据对象与簇中心的距离之差的平方总和最小,簇和簇之间的距离尽量拉大[11],数据对象间的相似程度以欧式距离为准则,采用方差作为目标函数,其定义为

K-means算法实现过程:
1)从样本集中随机指定k个点作为初始类簇中心;
3)重新计算每个集合的中心点;
4)新计算出来的中心点位置变化不大,趋于稳定,则聚类结束,反之循环上述步骤2)和3)。
3.2 改进的K-means聚类
将改进的FSDPC算法获取到的初始聚类簇中心在K-means算法中进行迭代,得到最终的微博聚类结果。实现过程如表1所示。

表1 聚类实现过程
4 实验过程与结果分析
4.1 实验过程设计
为验证改进后的算法在聚类效果上的优越性,分别用传统的K-means算法和本文基于密度峰值优化后的K-means算法应用于微博舆情分析实验中,然后根据实验结果对比分析,舆情分析应用的数据集情况见表2。
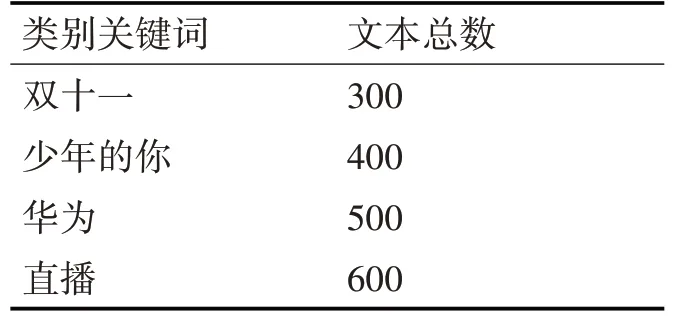
表2 实验数据集
舆情采集的爬取脚本用JavaScript语言编写,以微博中讨论较多,比较热门的话题作为关键词抓取数据。然后对文本集预处理,利用分词系统ICTCLAS对微博文档进行分词、搜集停用词表过滤掉已经淘汰的词语,建立微博文本的向量空间模型(Vector Space Model,VSM),使用向量空间信息检索范例提出的文本特征计算方法TF-IDF(词频-逆文档频率)来计算权重。
4.2 实验结果分析
本文采用F度量值作为聚类结果的评价标准。该方法结合了精确率(P)和召回率(R)两个指标,P和R分别由下面的计算公式得到[12]:

其中,TP为检索到的相关文本,即聚类的正确文档数,FP为聚类到的不正确的文本数,FN为未聚类到的正确的文本数,TP+FP表示所有相关的文本数,即聚类到的所有正确的文本总数,TP+FN表示用来聚类的文本总数。引出F度量值来综合精确率和召回率两个指标,度量值计算公式为
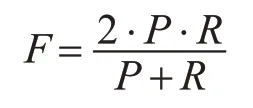
本文提出的算法和传统的K-means算法相比较,在F度量值和迭代次数上均有明显变化,实验结果如表3,表4所示。
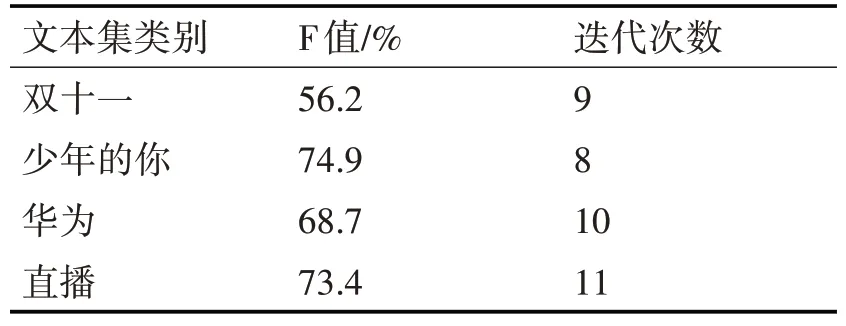
表3 传统的K-means算法的聚类结果
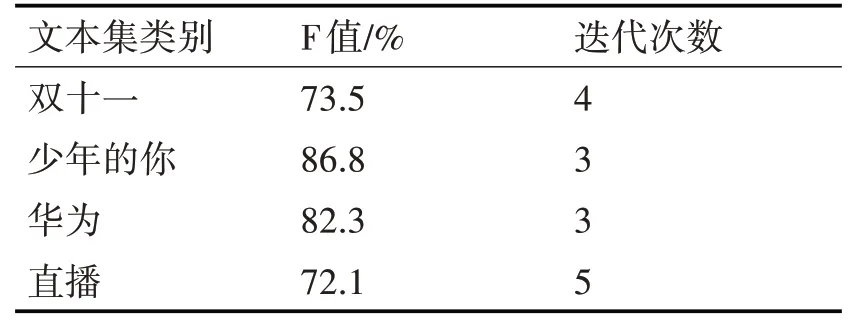
表4 本文算法的聚类结果
从表3,表4的结果对比可以看出,改进后的算法聚类效果对比传统的K-means算法,虽然有一类别F值稍稍偏低,但其他三类都明显高于传统K-means算法,在迭代次数上,改进后的算法明显要少于传统的K-means算法,从而证明改进后的算法减少了聚类时间。由此可见,改进后的K-means算法微博聚类分析上具有更高的准确度,而且保证了分析结果的稳定性,提高了在舆情分析过程中的效率,在舆情热点话题上具有更好的挖掘效果。
5 结语
本文主要对微博不同类别的舆情进行聚类分析,为了提高聚类效果,克服K-means算法随机选取初始聚类中心的缺陷,引入密度峰值算法,并对其相关参数进行优化,在一定程度上提升了聚类算法的全局搜索能力,更加准确、高效地对微博舆情进行聚类分析。聚类结果表明,密度峰值优化后的K-means算法具有更好的聚类效果,能够更加精确地挖掘出微博的热点话题。
