分离式三箱梁车-桥系统气动特性风洞试验

杨凌波，华旭刚，王超群，陈政清

(湖南大学 风工程与桥梁工程湖南省重点实验室，长沙 410082)

0 引 言

在桥梁抗风研究中，三分力系数是分析静风稳定、抖振响应、驰振稳定性的重要参数[1-2]，而作用在主梁-列车系统上的静风荷载直接影响到列车在桥上运行时的舒适性和安全性[3-4]。因此，研究主梁-列车系统三分力系数变化规律是桥梁抗风设计中的重要环节。分离式三箱梁以其良好的颤振性能和通行能力正在成为超大跨度公铁两用桥梁的首选结构形式之一。

近几十年来，已有大量学者对大跨度桥梁的车桥系统气动特性问题开展了风洞试验和计算流体力学（computational fluid dynamics，CFD）数值模拟研究[5-6]。在研究车桥系统气动特性时，风洞试验大多采用动态天平测量列车气动力，而常规天平无法测得脉动气动力或者测得的脉动气动力精度难以保证。何旭辉和邹云峰等[7-8]通过同步测压技术和动态天平测力方法对CRH2列车气动特性进行测试。试验结果表明当列车表面风压测点数量适当时，由风压积分可获得与天平测力精度相当的定常气动力，为测试列车气动力提供了一条新的思路。王玉晶等[9]针对高速列车在箱梁、T梁和路基三种不同结构形式上运行的系统模型进行节段模型试验，采用压力积分法计算作用在车辆上的气动力，分析了不同车况和线路构造形式及设置不同风屏障后的车桥气动特性。以上研究均表明车桥间的气动干扰对车辆和桥梁三分力系数影响显著。

韩艳等[10]基于CFD数值仿真平台，研究了静止车辆、风攻角和风场的紊流性对桥梁对车辆静气动力的影响。Wang等[11]通过CFD数值模拟，研究了侧风力作用下车辆模型受桥梁干扰的气动特性。通过CFD方法可以得到桥梁和车辆的静气动力，但桥梁的断面形式往往较简单，其计算网格的划分和边界条件容易确立。对于结构断面较为复杂的桥梁，可能存在多体结构气动干扰的情况，CFD方法有时难以保证计算精度，需要结合风洞试验来测试桥梁和列车的气动力。Wang等[12]通过风洞试验对高速列车通过桁架桥时的气动力进行了测量，还引入了CFD数值模型，分析了风速、风攻角和列车速度与列车所受到气动力之间的关系。

由于常规风洞试验无法做到雷诺数与实际结构一致，风洞试验得到的结构振动响应和三分力系数与实际结构存在着较大的差异，随着桥梁跨度的增加，主梁断面雷诺数效应的研究越来越重要。Schewe等[13]通过风洞试验发现导致风洞试验与现场实测的涡激振动起振风速不一致的原因是Strouhal数的雷诺数效应。任若松等[14]以两个常用的大跨度桥梁标准流线型桥梁段面为研究对象，利用压力积分法获得不同雷诺数下的三分力系数，发现桥梁断面局部细微差异不影响三分力系数随雷诺数的变化规律。Laima等[15]采用了大涡模拟（large eddy simulation，LES）方法研究了雷诺数对分离式双箱梁流动特性的影响，发现分离式双箱梁的扰流特性随流动区域和流动状态的不同而表现出不同的雷诺数效应。

分离式三箱梁具有良好的颤振稳定性和通行能力（梁宽较大），在未来人类征服更加宽阔的海峡、河谷过程中，特别是对于主跨超过2000 m的超大跨度公铁两用桥梁而言，具有广阔应用前景。而目前关于分离式三箱梁桥车桥系统气动特性问题的研究鲜有报道[16-17]，Wang和Yang等[18-20]对分离式三箱梁的气动特性和车桥系统的气动干扰效应做了初步的研究。主跨为3300 m的意大利墨西拿海峡大桥是最早采用分离式三箱梁方案的大桥，但由于资金匮乏，该项目至今尚未实施。在该桥的方案设计过程中，Diana教授对流线性断面分离式三箱梁的气动性能进行了一系列试验研究[21-23]。正在建设的甬州铁路桃夭门公铁两用大桥（斜拉桥，主跨666 m）和西堠门公铁两用大桥（斜拉-悬索体系，主跨1488 m）是世界首次采用分离式三箱梁的桥梁。由于分离式三箱梁断面构造复杂，可以推测其流场特性可能会比普通流线型断面乃至分离式双箱梁更为复杂。此外，作为典型的分离式结构，分离式三箱梁的雷诺数效应问题也特别值得关注。

依托在建的甬州铁路工程背景，本文对分离式三箱梁主梁-列车系统开展了节段模型测力风洞试验。测试了多种车桥组合工况下桥梁和列车的静力三分力系数，分析了腹板形状对分离式三箱梁断面三分力系数的影响和附属设施对主梁断面三分力系数的影响，研究了不同腹板形式主梁气动力的雷诺数效应，讨论了列车与主梁间的气动干扰效应，为同类型桥梁的抗风设计和研究提供参考。

1 试验方案

1.1 试验模型及设备

风洞试验在湖南大学风工程试验研究中心HD-2边界层风洞进行，该风洞试验段截面尺寸为3 m（宽）×2.5 m （高）。该试验段的来流为均匀流，3 m/s以上风速时湍流度不大于0.5 %。

在三分力测试试验中，主梁和列车节段模型只需模拟其断面几何外形。图1给出了三种不同腹板形状的分离式三箱梁断面，三种断面除了腹板形状有所区别外（前两种采用直线型腹板，后一种采用圆形腹板），其他几何特性基本相同。三种断面梁宽65.6～66 m（小倒角断面梁宽65.6 m，其他两种断面宽66 m），梁高4.5 m，中间铁路梁宽13 m，两侧公路箱宽19 m，箱梁断面见图2。主梁和列车节段模型采用1 ∶ 60缩尺比，主梁模型宽B= 1.1 m，模型高为H=0.075 m，模型的总长度取为L= 2.4 m。列车原型为CRH3动车组，模型断面宽b= 0.0544 m，高h=0.0604 m（不含车轮高度），列车模型与桥梁节段模型之间没有接触，模型安装见图3。

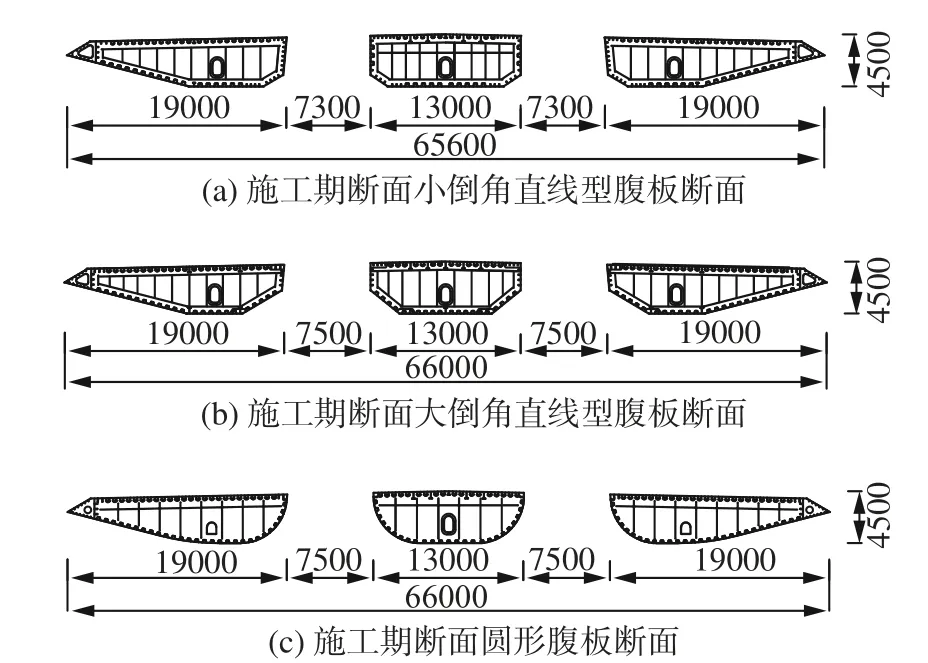
图1 施工状态下具有不同腹板形状的三种主梁断面 (单位：mm)Fig. 1 Cross sections of the bare girder with different web shapes (unit: mm): (a) section Ⅰ; (b) section Ⅱ; (c) section Ⅲ

图2 分离式三箱梁断面气动力示意图Fig. 2 Schematic diagram of the aerodynamic forces on the triple-box girder

图3 主梁节段模型安装示意图Fig. 3 Installation diagram of the girder model

数据采集系统由2个六分量高精度天平和三维超声波风速仪组成。试验采用的三维超声波风速仪型号为Young 81000，风速测试精度为0.05 m/s，采样频率为10 Hz。试验时，将模型通过特殊设计的基座装置（图4）水平安装在六分量高精度天平上，直接测量特定风速和风攻角下作用在模型上的三分力时程并计算各分量的平均值，进而获得该风攻角下无量纲三分力系数。低风速下测得的试验数据处于天平量程偏小的区间，为了验证其精度，进行了天平量程偏小区间的验证，确认了试验数据的准确性。由于测力天平数量有限，试验中两个和天平外观相似、尺寸一致的圆柱形连接件和天平按照图4的布置与桥梁模型支座以及列车模型支座相连。当需要测试车桥系统中主梁的三分力时，将天平和主梁模型支座相连，圆柱形连接件和两个列车模型支座相连。当需要测试某一侧列车时，将天平和对应的列车模型支座相连，圆柱形连接件和另一个列车模型支座以及桥梁模型支座相连。

图4 测力基座装置Fig. 4 Aerodynamic force measurement support

1.2 试验工况

表1列出了主梁节段模型（无列车）测力试验的工况。试验风攻角在−12°～12°之间变化，变化步长为1°。在主梁处于±12°风攻角时阻塞率为9.1 %。阻塞率会影响主梁截面表面的压力分布和流场结构，试验中应尽量减小阻塞率（抗风规范中建议阻塞率小于5%）。有研究成果表明[24-25]，当阻塞率为10%以下时，对方形横截面主梁的三分力系数和涡振性能影响较小，相对于低阻塞率不会产生较大的差异。对于扁平箱梁而言[26]，阻塞率大于5%会有明显的阻塞效应，三分力系数相对于低阻塞率有很大的差异。本文的模型断面高宽比很小，过小的模型难以模拟主梁断面和附属设施的细节（如列车轨道、风屏障栅格等），且小比例模型带来的雷诺数效应可能会更加明显，进一步影响测试结果的准确性。鉴于此，本研究没有采取更小的缩尺比进行试验。由文献[27]给出的修正公式得到本文模型在12°和−12°风攻角下的动压修正系数(1+εs+εW)2分别为1.143和1.092，其中εs表示固壁阻塞系数，εW表示尾流阻塞系数。阻塞率对三分力系数的影响将在后续的工作中进一步研究。

表1 主梁节段模型测力典型工况Table 1 Test cases for the aerodynamic force measurement of the girder model

本文模型外衣用ABS板做成，内部用三根芯梁和横梁骨架组成。由于做工误差，主梁模型某处局部的刚度较低，并且测力基座装置中的连接件的刚度偏低，无法完全满足刚性试验条件。在更高风速测试过程中，大风攻角下桥梁节段模型出现了明显的涡振。为了保证测试精度，本试验采用了节段模型在所有风攻角下均不发生涡振的较低风速（2.22 m/s、3.15 m/s和4.05 m/s）进行测试，测力试验在均匀流下进行，湍流度小于0.5%。为了对比腹板形状对气动力特性的影响，分别对三种不同腹板形状的施工期断面进行了测试。值得一提的是，作者在分离式三箱梁涡振性能试验研究中对主梁原始设计进行了气动优化，因此本文在成桥状态测力试验中对优化前及优化后的主梁（小倒角断面）均进行了测试。采取的气动措施包含[28]：将公路梁总高度3 m的防撞护栏+条形风屏障方案改为1.5 m高的防撞护栏 50 %透风率和3.6 m高的格栅形风屏障方案（总高度4 m）；将公路梁两道检修轨道移至内侧腹板正下方位置；在公路梁风屏障外侧布置9.4 cm高检修轨道；封闭公路梁内侧防撞护栏中间1/2高度；采用35 %透风率格栅封槽。

表2为不同腹板形式主梁气动力的雷诺数效应工况。为了避免主梁发生涡振，试验测试了在0°风攻角下不同腹板主梁在雷诺数为1.65×105～6.85×105时的三分力系数，采用的试验风速分别是2.23 m/s、6.10 m/s、8.00 m/s和9.30 m/s。

表2 不同腹板主梁三分力系数雷诺数效应工况Table 2 Test cases for the Reynolds number effect of the girder with different webs

桃夭门大桥为双线铁路桥，列车和桥梁（成桥状态有气动措施）存在多种工况组合。表3为成桥状态（小倒角断面，包含封槽、封栏杆等气动措施）车桥气动干扰测力的试验工况。由于车桥气动干扰测力试验在风攻角−3°、0°和3°时桥梁和列车模型均未发生明显风致振动，因此，选取10 m/s、15 m/s和20 m/s三个风速分别进行测试。

表3 主梁-列车系统气动干扰测力试验工况Table 3 Test cases for the aerodynamic force measurement of the girder-train system

1.3 三分力系数定义

主梁和列车的气动三分力坐标系的定义如图2和图5所示，需要说明的是，列车的力矩中心定义在两个列车轨顶（即列车轮底）高度中心处。主梁断面风轴坐标系下的三分力系数定义如下：

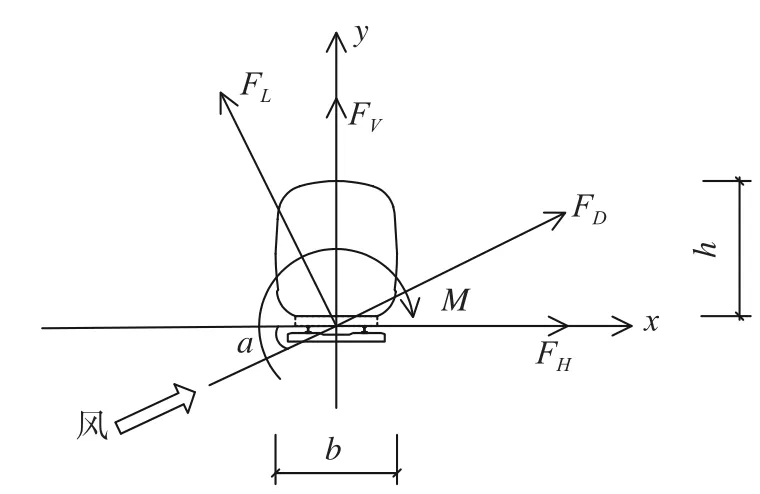
图5 列车三分力示意Fig. 5 Aerodynamic forces on the train

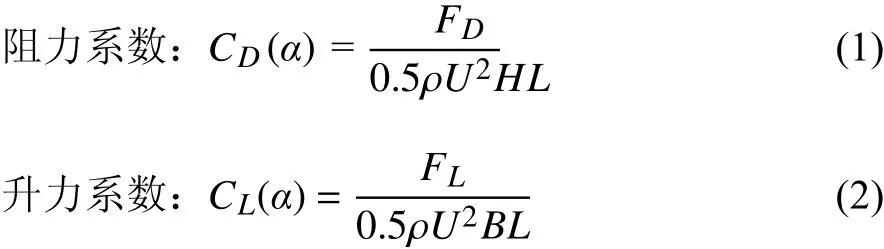
主梁断面体轴坐标系下三分力系数与风轴系下的三分力系数之间的转化关系为：

力矩系数在风轴坐标系和体轴坐标系下的表达式相同。其中，U为试验风速，空气密度ρ=1.225 kg/m3，L为测力节段模型长度；阻力系数以主梁高度H为参考长度，升力系数、力矩系数均以主梁断面的宽度B为参考长度。CD(α)、CL(α)、CM(α)分别为α风攻角时风轴坐标系下的阻力系数、升力系数和力矩系数。CH(α)、CV(α) 分别为风攻角α时体轴坐标系下的阻力系数、升力系数。

2 主梁三分力系数测试结果

如表1所示，主梁节段模型共进行了五种状态的试验测力试验。为了方便对比，本文所有桥梁三分力系数均采用相同的高度和宽度进行定义（宽B= 1.1 m，高H= 0.075 m，不含风屏障、防撞栏杆及检修轨道等附属设施高度）。

2.1 施工状态主梁三分力系数

图6给出了施工状态不同腹板主梁的三分力系数测试结果。由图6可知，三种不同腹板主梁三分力系数随风攻角的变化规律较为一致，即先减小后增大。对于施工状态的主梁，阻力系数在负攻角时较大，在−1° ～ 10°风攻角范围内，三种腹板主梁的阻力系数均小于1。大倒角和小倒角直线型腹板主梁阻力系数的最小值分别出现在α= 5°和α= 6°，圆形腹板主梁的阻力系数在α= 4°时最小。在−12°～10°风攻角变化范围内，三种不同断面主梁的升力系数和力矩系数曲线斜率都为正，说明施工期主梁有较好的颤振稳定性[29-30]。风攻角在10°～12°变化范围内，三种腹板形状主梁的升力系数和力矩系数曲线斜率均为负，随着攻角进一步增大，若超大跨度（数千米）桥梁采用分离式三箱梁断面，可能会发生驰振和单自由度扭转颤振[31]。由图6可见，主梁在施工状态不同断面下的静力三分力系数差异不大，说明腹板形状对分离式三箱梁的三分力系数影响很小。

图6 施工状态不同断面下主梁三分力系数Fig. 6 Aerodynamic force coefficients of the bare girder with different web shapes

2.2 成桥状态主梁三分力系数

为方便对比，图7给出了主梁节段模型在成桥状态下（小倒角断面），主梁有无气动措施三分力系数以及施工期静力三分力系数随风攻角变化的曲线。将工况1（施工期小倒角）和工况5（成桥状态有气动措施）的主梁三分力系数曲线放在一起比较。从图7可以发现，风攻角从最小−12°变化至最大12°时，两种状态下主梁的阻力系数变化趋势都是先减小后增大，而施工状态小倒角断面主梁的阻力系数增大的趋势滞后了许多。两种状态下的升力系数和力矩系数随风攻角变化的趋势一致。由于栏杆、风屏障等附属设施的存在，主梁阻力系数数值整体增大，可见成桥状态下的主梁较施工状态下的主梁受到的静风阻力更大。

图7 成桥状态主梁三分力系数(小倒角断面)Fig. 7 Aerodynamic force coefficients of the girder (section Ⅰ)

从图7可以看出，在成桥状态下增加气动措施之后会引起三分力系数的改变。成桥无气动措施时，主梁的三分力系数曲线−8°～0°风攻角区间内存在明显波动，且在−8°到−7°处出现明显突变，推测是多体断面流场结构形态的变化[32]，王光崇[33]研究的分离式双箱梁的阻力系数和升力系数曲线在−5°也发生了突变，其中的机理需要通过流场显示，利用CFD数值模拟和PIV（Particle Image Velocimetry）可视化技术进一步研究。

当风攻角从−8°到−7°，成桥状态下未增加气动措施主梁的升力系数曲线斜率从正变为负，可能引起驰振。在增加气动措施之后，三分力系数随风攻角变化的曲线变得更加平滑。可以看出，格栅封槽等气动措施在改善主梁的涡振性能[28]的同时，使得主梁的三分力系数随风攻角变化的曲线变得相对平缓。在风攻角−12°～−9°范围内，成桥状态下主梁的力矩系数曲线斜率为负，可能引发单自由度扭转颤振。

成桥有气动措施时，主梁的阻力系数与王光崇[33]和郭夏[34]得到的分离式双箱梁阻力系数随风攻角变化的趋势均比较接近，即先减小后增大且拐点大约在风攻角为−2°到0°之间；所测风攻角范围内，主梁的升力和力矩系数曲线斜率大多数为正，和一般扁平箱梁和分离式双箱梁变化规律基本一致[34]。

2.3 主梁雷诺数效应

图8给出了攻角0°下施工期大倒角直线型腹板主梁和圆形腹板主梁的静力三分力系数随雷诺数的变化情况。从图8（a）可见，大倒角直线型腹板和圆形腹板主梁的阻力系数在雷诺数1.65×105～6.85×105有明显波动。大倒角直线型腹板主梁阻力系数随雷诺数增加而减小，阻力系数由从0.897下降到0.678，下降幅度为24.4 %。圆形腹板主梁阻力系数高于大倒角腹板主梁，随着雷诺数的增加，阻力系数出现先减小后增大的趋势。在雷诺数为5.87×105时阻力系数最小数值为0.798，相较于最大时的1.171减小31.9 %。

图8（b）中可见，两种腹板形式主梁的升力系数在试验雷诺数范围内无明显波动，圆形腹板主梁升力系数数值高于大倒角腹板主梁，在雷诺数为6.85×105时最大差值为0.063。对比图8（c），圆形腹板主梁的力矩系数随雷诺数的增加而减小，力矩系数由0.038降低到0.027，变化幅度为28.9 %。大倒角腹板主梁的力矩系数无明显变化。在雷诺数为6.85×105时，两种腹板形式主梁的力矩系数相近。

图8 不同腹板形式主梁的雷诺数效应比较Fig. 8 Comparison of the Reynolds number effect for the girder with different webs

在一定雷诺数范围内，两种腹板形式主梁的三分力系数随雷诺数的变化趋势差异较大。大倒角直线型腹板主梁阻力系数随雷诺数的增大呈下降趋势，升力系数和力矩系数并无明显的变化趋势。圆形腹板主梁的阻力系数和力矩系数随雷诺数变化有较大波动，力矩系数无明显变化。

3 车桥系统试验结果分析

3.1 不同来流风速的影响

桥梁节段模型风洞试验中, 因桥道断面较为钝化、绕流分离点较为固定, 试验中一般可忽略雷诺数的影响[35-36]。CRH3列车断面虽近似矩形, 但周边采用弧形圆滑断面, 其绕流分离点与雷诺数有关。已有研究[37]表明在车—桥系统定常气动力测试中通常可忽略雷诺数的影响。

表4对比了当列车处于迎风侧时不同风速下0°风攻角的车桥系统三分力系数（主梁为小倒角断面）。测试结果表明，列车-主梁系统在不同风速下的三分力系数差别很小，即雷诺数的影响很小。因此，表5～表7中给出的测试结果均为所有测试风速下三分力系数的均值。为便于比较，在本节中所有主梁三分力系数均采用相同的高度和宽度进行定义，宽B= 1.093 m，高H= 0.075 m（不含风屏障、防撞栏杆及检修轨道等附属设施高度）。

表4 不同风速下的主梁与列车三分力系数Table 4 Aerodynamic force coefficients of the girder and the train under different wind speeds

表5 仅列车/主梁的三分力系数Table 5 Aerodynamic force coefficients of the single train or the girder

3.2 单列车-主梁系统

为分析车桥系统车辆和主梁气动力的相互影响，首先测试了0°攻角下仅桥梁的三分力系数，相关结果如表5所示。需要说明的是，表5中列车模型的三分力系数来自参考文献[38]，文献中的列车模型采用CRH2列车，宽为0.076 m，高为0.074 m，与本文中CRH3列车断面气动外形相似，CRH2和CRH3列车在低风速下测得的阻力系数差异较小[39]。

为研究单列车处于主梁不同位置时主梁-列车系统列车和主梁气动力的相互影响，将0°风攻角下单列车在不同车道时列车与主梁三分力系数进行对比分析。如表6所示，当列车处于主梁上时，由于公路梁风屏障（2.5 m高50%透风率的风屏障+1.5 m 高防撞护栏，总高4 m））和铁路梁风屏障（50%透风率，高度3.6 m）的双重减风作用，列车的阻力系数显著降低[40]。试验中的列车是静止的，静态列车模型模拟动态列车会导致风偏角和实际风偏角不符合，对高速列车通过桥梁时的气动特性估计不准确[13]。关于风偏角对列车气动性能的影响将在后续的工作中进一步研究。

表6 主梁系统三分力系数(单列车)Table 6 Aerodynamic force coefficients of the train-girder system (single train)

列车的存在使主梁的阻力系数略有降低；列车位于迎风侧（车道1）和背风侧（车道2）时，由于列车离主梁前缘较远且几乎处于主梁形心上方，列车位于迎风侧或背风侧对主梁的影响差别不大；列车的存在改变了主梁上缘流场结构，使主梁的升力系数数值略微增大；车桥之间的气动干扰对主梁的力矩系数影响较小。

3.3 双列车-主梁系统

由于桥梁为双线铁路桥梁，可能出现双车交会的情况。风攻角0°、两列车同时存在时列车与主梁的三分力系数如表7所示。

表7 主梁系统三分力系数(双列车)Table 7 Aerodynamic force coefficients of the train-girder system (double trains)

对比表7、表6和表5可以发现，与单列车-主梁系统类似，双列车的存在使主梁的阻力系数显著减小，而升力系数和力矩系数较之变化不大。单列车位于迎风侧时的列车和双列车时位于迎风侧的列车，两者的阻力系数和力矩系数十分接近，前者的升力系数要小于后者。双车同时存在时，由于迎风侧列车的遮挡效应，背风侧车辆的气动力显著减小，与李永乐等[41]的研究结果一致。当双车交会时，背风侧列车受到的力突降，会车后，背风侧列车受到的风荷载又突增。在整个会车过程中，列车风荷载突降又突增，影响列车的稳定性，对行车的舒适性和安全性极为不利。

3.4 不同风攻角对列车-主梁系统的影响

图9给出了在−3°、0°和3°风攻角下，无列车、单列车存在和双列车同时存在时主梁的三分力系数。从图9可知，在−3°、0°和3°三个攻角下，相对于无列车影响的主梁，迎风侧列车存在时，主梁的阻力系数分别下降了17.3 %、10.1 %和8 %。双列车的存在导致主梁的阻力系数分别下降了43.9 %、29.1 %和57.3 %。在±3°攻角下，列车的气动干扰使主梁的力矩系数数值降低。在不同风攻角下，列车的存在相对于无列车时会使主梁的升力系数值提高。在攻角0°下，列车的存在使主梁的力矩系数数值略有增大。

图9 不同攻角下列车对主梁三分力系数的影响Fig. 9 Effect of trains on the aerodynamics force coefficients of the girder at different wind attack angles

4 结 论

本文对分离式三箱梁桥主梁-列车系统开展了节段模型测力风洞试验，测试了多种车桥组合工况下桥梁和列车的静力三分力系数，研究了气动干扰效应。主要结论如下：

1）直角或曲线腹板形式对分离式三箱梁的三分力系数影响很小。在风攻角10°～12°范围内，施工期主梁的升力系数和力矩系数为负，对于主梁可能产生较大静风位移的超大跨度桥梁而言，有发生驰振和单自由度扭转颤振的风险。

2）成桥无气动措施时，分离式三箱梁在风攻角从−8°变到−7°时，主梁的升力系数斜率从正变为负，可能发生驰振；在风攻角−12°～−9°范围内，主梁的力矩系数曲线斜率为负，可能发生单自由度扭转颤振；三分力系数曲线出现突变，推测是多体断面流场结构形态的变化。

3）气动措施对分离式三箱梁的三分力系数影响较大。封槽盖板等气动措施使主梁的三分力系数曲线变得更加平滑；成桥状态分离式三箱梁的三分力系数随风攻角的变化规律与分离式双箱梁和一般扁平箱梁十分接近。

4）不同腹板形式主梁的三分力系数在一定雷诺数范围内随雷诺数的变化趋势差异较大。大倒角直线型腹板主梁阻力系数随雷诺数的增大呈下降趋势，升力系数和力矩系数并无明显的变化趋势。圆形腹板主梁的阻力系数和力矩系数随雷诺数变化有较大波动，力矩系数无明显变化。

5）列车与分离式三箱梁间存在显著的气动干扰，且不同风攻角间存在明显差异。单个列车存在时，列车所处的轨道位置对主梁的三分力系数影响不大；当两列车相遇时，主梁的阻力系数较无列车和单列车工况明显减小。列车的存在对主梁的升力系数和力矩系数影响不大。双列车会车时，背风侧列车受到的气动力先突降后突增，对行车安全不利。