高速地铁通过隧道车外压力波研究

陈大伟，丁叁叁，宋军浩，姚拴宝

(中车青岛四方机车车辆股份有限公司，青岛 266111)

0 引 言

随着社会的发展和生活水平的提高，人们的出行压力越来越大，地铁作为解决城市交通压力的有效工具，具有大通勤量和高效率等特点，可以有效地解决城市地面交通阻塞问题，近年来得到了飞速发展。目前各大城市都建有或在建城市轨道交通系统，地铁列车的最高运行速度也从80 km/h逐渐提高到160 km/h，如广州地铁3号线、郑州地铁郑许线最高运行速度120 km/h；成都地铁18号线最高运行速度140 km/h；北京地铁大兴新机场线最高运行速度160 km/h。

随着运行速度的提高，隧道内空气与列车间的相互作用产生的隧道压力波问题变得越来越显著。高强度的压力波由车外传至车内引起司机和乘客耳膜出现不适症状，严重时会对人体健康造成影响。目前关于隧道压力波的研究大多集中在高速动车组方面[1-5]，地铁列车速度较低时，隧道空气动力学效应不明显，对地铁列车通过隧道产生压力波的研究较少。梅元贵[6]对特长隧道和中长隧道两种条件下的车外瞬变压力和车内压力波动特性进行研究，归纳了隧道长度、列车速度和气密性指数对车内压力变化的影响特性。冉腾飞[7]采用三维非定常数值计算方法对地铁列车由明线驶入隧道及站间运行时产生的最大车体表面峰峰值进行了分析比较。徐世南[8]对地铁车辆通过最不利长度隧道时的空气动力学性能进行数值模拟，得到并分析了车体表面压力峰峰值与列车速度和隧道净空面积关系。骆建军[9]对区间隧道段内设置扩大段+通风竖井组合式缓解设施改变高速地铁隧道内瞬变压力的作用进行了研究，结果表明合适的扩大段位置和增大断面积可以有效的缓解隧道内的压力和压力梯度。杨伟超[10]对地铁内列车的运行过程进行了模拟，分析了中间风井和区间隧道通风对车体压力的影响。

本文结合高速地铁运行隧道一般结构，建立地铁列车模型和隧道模型。采用数值仿真方法对列车通过隧道压力波进行了仿真分析，研究不同运行速度、隧道断面面积、编组形式、隧道长度等对车外压力波动幅值影响规律。

1 数值计算方法

1.1 数学模型

列车通过隧道时，隧道内空气受到列车和隧道壁面空间的限制而受到挤压，须将空气视为可压缩的理想气体。因此，计算采用三维、非定常、可压缩的时均Navier-Stokes方程和标准k-ε两方程湍流模型。计算采用Fluent 14.0，压力速度修正采用SIMPLEC算法，对流项采用高阶精度的二阶迎风格式离散，扩散项采用二阶中心格式离散。

1.2 计算模型

计算模型采用采用四辆编组B型地铁列车，几何模型做适当简化，忽略转向架的影响。列车编组图如图1所示，头、尾车对称分布，长度均为20 m，中间车长度19 m，横截面投影面积为9.071 m2。车外压力测点以四编组为例共16个，其中头、尾车各5个，每节中间车3个。如果编组加长，头、尾车测点位置不变，中间车的测点数量依照每节车3个逐渐增加，测点位置位于车厢中间区域。

图1 列车几何模型及测点布置Fig. 1 Geometry model of the train and the measurement point layout

隧道模型断面根据现有断面情况，如图2所示。净空面积为26.63 m2，地铁B 型车与隧道截面的阻塞比为0.341。

图2 隧道模型断面Fig. 2 Cross section of the tunnel model

1.3 计算域及边界条件

为模拟列车通过隧道的相对运动过程，采用滑移网格法进行模拟。计算域如图3，外场区域为半圆形远场，长度为250 m，高度为50 m，宽度为100 m，隧道长度与计算工况保持一致。

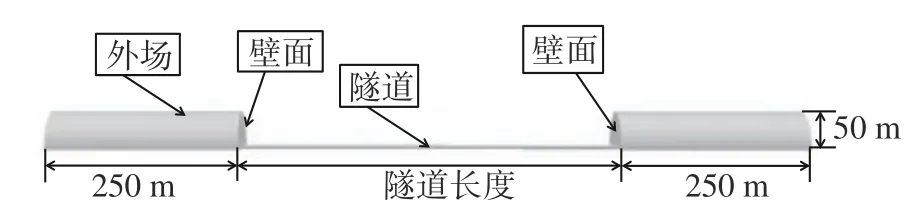
图3 计算区域Fig. 3 Computational domain

采用ICEM CFD划分计算区域的空间网格，列车模型结构复杂，采用非结构网格进行离散，头部和风挡区域单独加密，外场区域采用结构化网格，计算网格如图4。

图4 计算网格Fig. 4 Computational grid

边界条件：外场均为压力出口，出口压力为101325 Pa，靠近隧道的两侧壁面均为固壁边界，列车、隧道和地面也为固壁边界。若无特殊说明，列车均从距离隧道入口100 m的位置匀速进入隧道。

2 数值方法验证

为验证列车隧道压力波数值计算方法的准确度，利用中国科学院力学研究所的高速列车双向动模型实验平台测试列车通过隧道时的压力波试验数据，进行相同工况的数值仿真计算。

考虑到目前缺乏地铁列车的隧道压力波试验结果，且不同类型列车、不同速度等级下的列车隧道压力波计算方法是相同的。本文数值计算方法验证采用的列车模型是CRH380A。试验模型为缩比尺寸为1∶8的三辆编组CRH380A，列车运行速度为310 km/h，隧道长度为60 m，隧道净空面积为1.56 m2。车体表面测点位于中间车长度方向中心位置，图5给出了车体表面压力随时间变化的试验数据（红线）和数值计算结果（黑线），可以看出：数值计算结果与试验数据的压力波曲线基本一致，动模型试验的压力波幅值为3 556 Pa，数值计算得到的压力波变化幅值为3490 Pa，相对误差为1.9%，表明本文采用的计算方法和网格离散方法能够较为准确的模拟列车通过隧道时的压力变化。

图5 列车车体表面测点压力随时间的变化曲线Fig. 5 Time variation of the pressure at the measurement points of the train surface

3 计算结果及分析

以下主要对列车速度、阻塞比、隧道断面形状、列车编组形式、隧道长度进行分析。

3.1 列车速度

不同速度在最不利隧道长度条件下隧道通过的车外压力波动曲线如图6所示。不同速度下隧道压缩波、膨胀波叠加至车身的变化使测点压力波动趋势有所不同。可以看出：运行速度越高，车外压力波动越显著；对于头车和中间车测点，列车进入隧道后产生的第一个车外压力波动峰峰值最大，对于尾车测点，列车进入隧道时产生的压缩波对该区域的压力波动影响可以忽略，而尾车进入后产生的膨胀波对该区域的压力波动影响较大，列车进入隧道后产生的第二个压力波动峰峰值对尾车车外压力波动的影响最大。列车出隧道时产生的车外压力波动较弱，对列车影响很小。

图6 列车表面测点在不同运行速度条件下的压力波动曲线Fig. 6 Pressure fluctuation at the measurement points of the train surface for different running speeds

不同速度等级条件下的车外压力波如图7，隧道断面为矩形断面，净空面积为26.63 m2，可以看出：列车运行速度越高，车外压力波动峰峰值和最大值越大，最小值的绝对值越大；在各个速度等级条件下，越靠近头车，车外压力波动越显著；对于不同速度、不同位置的测点，压力最小值的贡献量都显著大于压力最大值的贡献量，即负压占主导位置；对于压力峰峰值，列车运行速度越高，压力峰峰值对速度的变化越灵敏，对于测点H3和M1，车外压力峰峰值与列车运行速度的2.7次方成正比，对于测点M4，车外压力峰峰值与列车运行速度的2.6次方成正比，对于测点T1，车外压力峰峰值与列车运行速度的2.9次方成正比。

图7 列车表面测点在不同运行速度下的压力波动幅值Fig. 7 Pressure fluctuation amplitude at the measurement points of the train surface for different running speeds

3.2 阻塞比

阻塞比是指车体正向投影面积与隧道净空面积的比值，定义为，和分别对应列车横断面积和隧道横断面积，该参数是影响列车车外压力波动的关键参数之一。为分析阻塞比对隧道压力波的影响，图8给出了不同阻塞比条件下的测点M1处的车外压力波动，可以看出：不同速度条件下，车外压力波动随阻塞比的变化趋势基本一致。随着阻塞比的增大，最大值、最小值和峰峰值均逐渐增大，且阻塞比越大，车外压力波动的增大幅度越显著。从列车以120 km/h通过隧道压力波数据可以看出：与阻塞比为0.2的车外压力波动相比，当阻塞比增大为0.45时，车外压力的最大值、最小值和峰峰值的绝对值分别增大91.4%、75.9%和81.3%。

图8 不同阻塞比条件下的测点M1压力波动幅值Fig. 8 Pressure fluctuation amplitude at the measurement point M1 under different blockage ratios

3.3 隧道断面形状

图9给出了最不利长度条件下，运行速度为120 km/h时，列车通过两种断面隧道的车外压力波动。从图中可以看出：当隧道断面的净空面积不变时，隧道断面形状的变化对列车车外压力波动峰峰值、最大值和最小值的影响都可以忽略。

图9 不同隧道断面形状下的测点压力波动幅值（速度120 km/h）Fig. 9 Pressure fluctuation amplitude at the measurement points for different tunnel cross-section shapes (V = 120 km/h)

3.4 列车编组形式

地铁车辆的编组形式多样，对于同一种车型，不同的编组形式导致列车长度发生明显的变化。四编组、六编组和八编组三种编组形式以120 km/h速度通过最不利长度隧道得到的车外压力波动如图10。可以看出：头车区域测点的车外压力最大值显著大于尾车区域测点的最大值，而尾车区域测点的车外压力最小值显著小于头车区域测点的最小值，从头车到尾车，车外压力峰峰值逐渐减小。对于不同的编组形式，车外压力波动的变化趋势基本一致，编组越长，车外压力波动越剧烈。对于测点M1，与四辆编组相比，八辆编组列车的车外压力波动峰峰值、最大值和最小值分别增大12.6%、32.3%和3.5%，可见，最大值的变化幅度最大，最小值的变化幅度最小。

图10 不同编组形式下压力波动幅值沿列车长度方向分布（速度120 km/h）Fig. 10 Pressure fluctuation amplitude distribution along the longitudinal direction of the train for different formation forms (V = 120 km/h)

3.5 隧道长度

为了分析隧道长度对隧道压力波的影响，四编组列 车 以120 km/h通 过500 m、1000 m、2000 m和3000 m四种长度的矩形断面隧道测点M1处的车外压力波动如图11所示。可以看出：隧道长度为2 000 m时，车外压力波动的最大值、最小值和峰峰值均最为恶劣，从500 m到2 000 m变化时，车外压力波动的最大值、最小值和峰峰值的绝对值均逐渐增大。与隧道长度为500 m时的车外压力波动相比，隧道长度为2 000 m时，车外压力波动的最大值、最小值和峰峰值的绝对值分别增大2.1%、24.8%和17.6%。

图11 M1测点在不同隧道长度条件下压力波动幅值Fig. 11 Pressure fluctuation amplitude at the measurement point M1 for different tunnel lengths

3.6 入口缓冲结构

隧道口安装合理的缓冲结构能够减弱列车通过隧道时产生的车内外压力波动，并且可以降低隧道出口区域的微气压波。缓冲结构的设计参考城市地铁隧道缓冲结构型式，缓冲结构为喇叭型，长度为30 m，最大断面面积为40 m2，并考虑了无开口和开口两种型式，开口缓冲结构是在无开口缓冲结构的顶部设计了两个压力释放孔，如图12所示。

图12 隧道洞口缓冲结构Fig. 12 Hood structures at the tunnel opening ends

图13给出了不同缓冲结构条件下测点M1处的车外压力波动曲线，可以看出：各压力波动曲线的波动形式基本一致，列车进入隧道后产生的第一个压力波动峰峰值最为剧烈，安装缓冲结构之后，第一个压力波形的最大值降低。

图13 不同隧道缓冲结构下M1测点压力波动曲线Fig. 13 Pressure fluctuation at the measurement point M1 for different tunnel hoods

表1给出了不同缓冲结构类型对应的车外压力波动值，可以看出：安装缓冲结构之后，列车进入隧道时的压力波的最大值降低，而压力波的最小值变化不明显。安装缓冲结构可减弱列车进入隧道的第一个压力波峰值，进而有助于降低隧道微气压波。

表1 不同缓冲结构类型对应的测点压力波动幅值Table 1 Pressure fluctuation amplitude at the measurement points for different tunnel hoods

4 结 论

本文针对高速地铁列车通过隧道过程中车外压力波动，从运行速度、阻塞比、隧道断面形状、列车编组形式、隧道长度、缓冲结构形式方面进行了仿真分析研究，主要得到如下结论：

1）同一列车通过同一隧道，列车运行速度越高，车外压力波动越剧烈，车外压力波幅值约与速度2.6～2.9次方成正比。

2）随着阻塞比的增大，车外压力的最大值、最小值和峰峰值均逐渐增大，且阻塞比越大，车外压力波动的增大幅度越显著。与阻塞比为0.2的车外压力波动相比，当阻塞比增大为0.45时，车外压力的最大值、最小值和峰峰值的绝对值分别增大91.4%、75.9%和81.3%。当隧道断面面积不变时，同一列车以同一速度通过隧道时，断面形状对车外压力波的影响很小。

3）不同的编组形式，车外压力波动的变化趋势基本一致，编组越长，车外压力波动越剧烈。应根据最为关心的列车位置确定最不利隧道长度，对于列车不同位置的车外压力波动而言，最不利隧道长度也不同，对于工程实际问题，需要具体问题具体分析。

4）安装缓冲结构之后，列车通过隧道时的压力波的最大幅值降低，对压力波的最小幅值变化不明显。安装缓冲结构可减弱列车进入隧道的第一个压力波峰值，进而有助于降低隧道微气压波。