智能汽车转向避撞运动轨迹规划
2022-05-10刘忠强
刘忠强
(四川工程职业技术学院,四川 德阳 618000)
目前,国内外已有许多学者针对智能汽车避撞运动轨迹规划问题进行了深入研究。SANGWOO等人通过全面考虑车辆的位置、速度和方向等关键因素设计出一种人工势场,来解决智能汽车实时避撞轨迹规划问题。HILGERT J等人采用Elastic Band Theory理论规划出智能汽车的紧急避撞轨迹,以轨迹局部的曲率变化最小为规划约束要求,从而提高了紧急避撞时的行驶稳定性。FUNKE等人使用曲率连续变化的回旋曲线与圆弧组合方式规划智能车辆在紧急换道时的轨迹和避撞过程中车辆运动的横向位置与纵向速度,实验结果证实该方法能够适应更多极端工况。陈成等人在动力学、连续曲率、目标位置状态等约束下,采用四阶贝塞尔曲线规划出车辆避撞轨迹,同时在实际环境数据基础上进行实验测试。江浩斌等人首先采用Sigmoid函数规划一条紧急避撞参考轨迹,再采用hp自适应伪谱法以最小变道距离为目标对避撞换道轨迹进行优化,提高了智能汽车紧急换道轨迹规划的适应性和实时性。王斌基于汽车运动轨迹预测和行驶中的各种因素,对快速搜索随机树算法进行了改进,从而可以规划出满足平滑性和安全性的避撞轨迹,仿真结果证明该方法能够使汽车成功避开前方障碍车。张一鸣等人提出首先对前车的运动轨迹进行预测,再利用贝塞尔曲线来规划自车的运动轨迹,最后通过序列二次规划方法优化求解自车运动的目标位置,获得最优化的避撞运动轨迹。总体来说,汽车的避撞轨迹规划要以安全性约束、动力学约束为前提,并兼顾实时性和舒适性。
1 转向避撞场景分析
智能汽车在行驶中通过激光雷达、视觉传感器及车联网等实时采集各种路况信息,并结合主车位置和运行状态,首先根据主车与前车的距离值来判断能否通过纵向制动实现避撞。若采取纵向制动无法避开前方障碍车辆时,则要通过换道方式来实现转向避撞。
主车(Subject Vehicle, SV)在当前车道高速行驶,而前车(Forward Vehicle, FV)在当前车道低速行驶,并且两车车距较小,已经不能仅靠纵 向制动来避免发生碰撞。因此,需要向旁边车道转向换道来实现避撞目标,如图1所示。
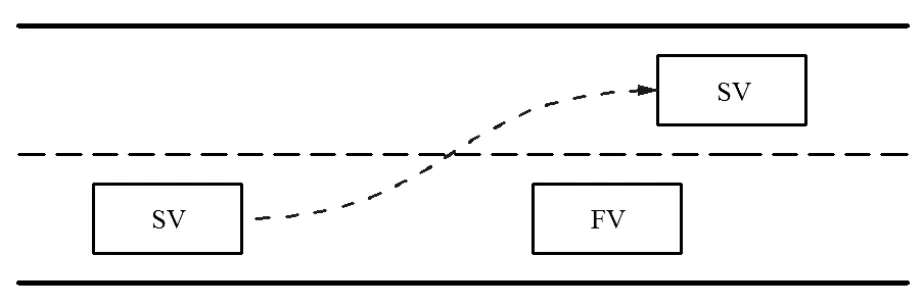
图1 转向避撞场景示意图
2 横向运动轨迹规划
由于汽车运行速度较高,为确保车辆转向换道时的平顺性,避免突然发生转向,大多使用多项式曲线方法来拟合描述车辆避撞轨迹。这种轨迹规划方法操作简单、实时性高,易于工程实际应用。因此,本文采用常用的五次多项式轨迹规划方法描述转向换道避撞时的横向运动规律。
设横向运动位移方程的一般形式为
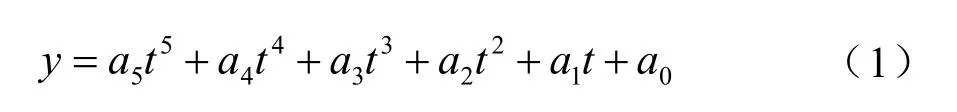
式中,为横向位移,为换道时间。
对式(1)求导,得横向运动速度方程为

对式(2)求导,得横向运动加速度方程为



标准车道宽度为3.5 m,设车辆纵轴线在转向换道的初始时刻和完成时刻均与车道宽度中心线重合,由车辆横向运动前后的边界条件可知,若初始时刻的状态为(0,0,0),则完成时刻的状态为(3.5,0,0)。由于汽车换道总时间一般小于15 s,若依次取转向换道避撞总时间为3 s、5 s、7 s,将参数代入式(4),则可分别得到如下系数矩阵。
当转向换道时间为3 s时,系数矩阵为

当转向换道时间为5s时,系数矩阵为
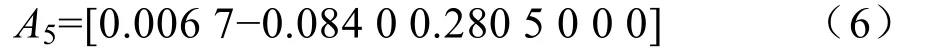
当转向换道时间为7s时,系数矩阵为
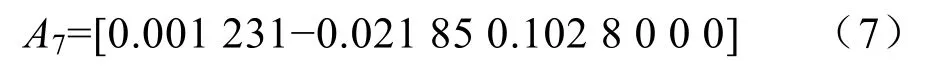
将式(5)—式(7)分别代入式(2),可得不同转向避撞时间下车辆横向运动速度与时间的关系曲线,如图2所示。将式(5)—式(7)分别代入式(3),可得不同转向避撞时间下车辆横向运动加速度与时间的关系曲线,如图3所示。从图2和图3可知,最大横向速度与最大横向加速度都随着转向避撞时间增大而减小,3 s时的最大横向速度与最大横向加速度远大于5 s和7 s时的最大横向速度与最大横向加速度,5 s和7 s时的最大横向速度与最大横向加速度比较接近。
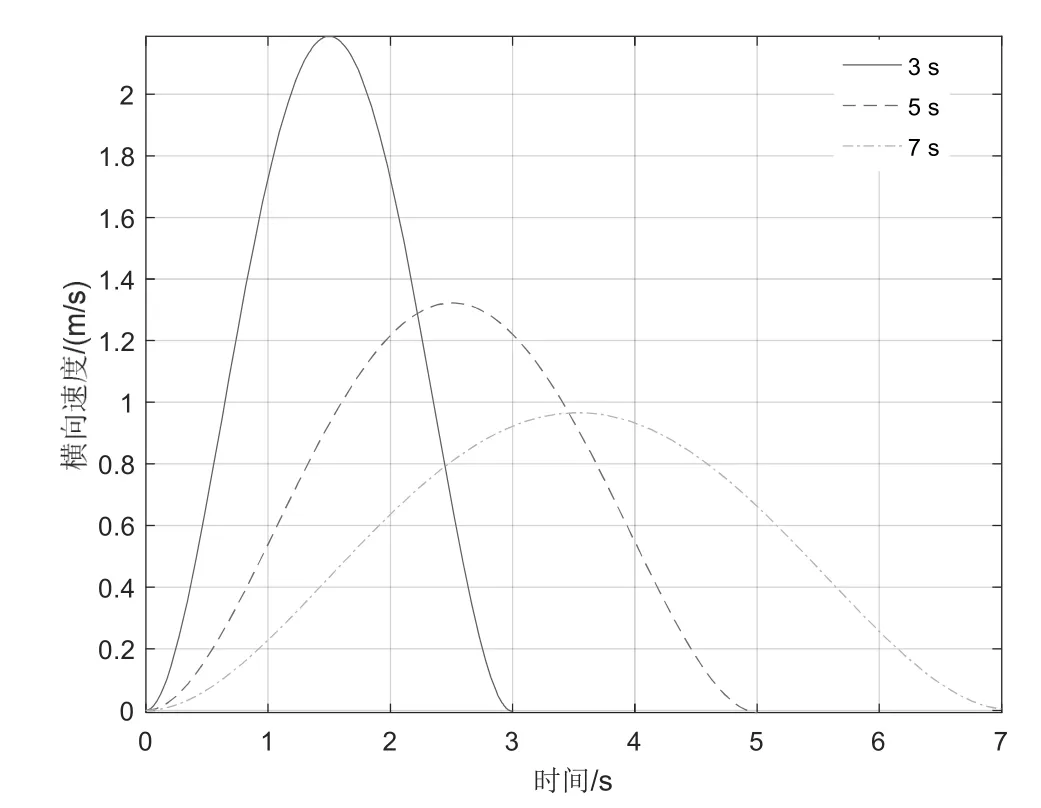
图2 横向运动速度与时间的关系

图3 横向运动加速度与时间的关系
3 纵向运动速度规划
以转向换道初始时刻的主车右后角点为坐标原点,建立直角坐标系,设主车SV右后角点坐标为(x,y),前车FV左后角点坐标为(,),如图4所示。

图4 转向换道避撞示意图
由于主车SV初始速度很高,所以在转向换道过程中采取纵向匀减速运动,前车FV为低速匀速直线运动,则经过时间后,可得各坐标表达式为

式中,为主车车身长度,为主车初始速度,为主车减速度。

式中,为主车与前车的距离,为前车速度,为前车车身宽度。
根据两车碰撞安全性约束要求,两点坐标需要满足条件如下:

式中,为主车车身长度,为两车安全距离。
设两车经过时间,实现y=y,将式(6)、式(7)代入式(8),则

考虑转向换道的轮胎地面动力学约束和平稳舒适性要求,这里选取转向换道避撞时间为5 s。设主车车身长度为4.8 m,前车车身宽度为1.8 m,前车行驶速度为50 km/h,安全距离为0.5 m,两车车距的范围取为0 m~35 m。当主车初始车速处于高速工况时,根据式(10)和式(11),则可建立主车车速分别为90 km/h、100 km/h、 110 km/h时纵向运动最小减速度与车距的关系曲线,如图5所示。图5表明两车距离越小,车辆纵向运动所需的最小减速度将快速增加;主车车速越高,车辆纵向运动所需的最小减速度也更大。若取主车车速为100 km/h,主车减速度分别为两车车距在25 m、30 m、35 m时对应的最小减速度,则根据式(8)可得转向换道避撞的轨迹曲线,主车车速确定时,两车初始车距越大,则车辆运动的纵向位移越大,如图6所示。

图5 纵向运动最小减速度与车距的关系

图6 转向换道避撞轨迹
4 结论
本文针对智能汽车转向避撞运动轨迹规划问题,从车辆运动学角度分别对车辆横向运动和纵向运动两个维度作了研究讨论,并未充分考虑车 辆动力学影响因素。其中针对纵向运动速度规划只讨论了前车为匀速直线运动的情况,而前车运行状态时刻都处于不断变化中,旁边车道也可能会出现通行车辆干扰的问题。因此,未来还应该基于转向避撞场景的实际工况进一步全面深入地研究运动轨迹规划问题,从而提高轨迹规划方法的可行性和适应性。
