基于改进层次分析-物元可拓的岩爆预测模型

侯克鹏　邵琳　李岳峰　乔木　王团辉

摘要：岩爆是岩土工程中棘手的地质灾害，预防预测是治理的关键。数学建模方法是岩爆预测领域的常用手段。论文结合层次分析法和物元可拓理论进行建模，用于工程中的岩爆预测。首先，对层次分析法进行改进，精简计算量;其次，对物元可拓模型进行改进，避免特征值超出节域时关联函数失效的问题;最后，将改进后方法结合建模并应用于白鹤滩水电站岩爆预测，预测结果与实际情况一致，是一种可靠易操作的岩爆预测模型。

关键词：层次分析法;物元可拓模型;分级预测;工程应用

中图分类号：TD31文献标志码：A

岩爆是开挖时岩石破坏造成的失稳并伴随着能量的猛烈释放的一种动力现象，主要发生在高地应力，高埋深，高地温等地质条件复杂的地区，爆发时常伴随着岩石的松动、剥落、弹射甚至抛出[1]，往往会造成人员伤亡和经济损失。通过预测进行预防是目前最佳防护手段。岩爆机理复杂，难以预测，研究人员引入大量的数学模型对其进行预测研究[2-8]，取得了较好的效果。层次分析法[9-17]与物元可拓模型[18-21]在岩爆预测领域应用广泛。

徐琛[9]、卢富然[10]、石晓燕和董源[11-13]等采用1～9标度层次分析法与熵权法相结合确定权重建立岩爆预测模型并应用于不同的工程中;殷欣等[14]采用1～9标度层次分析法与反熵权法相结合确定权重建立属性区间识别岩爆预测模型，取得了良好的效果;刘晓悦等[15]采用标度构造层次分析法与基于指标相关性的指标权重法（criteria importance through intercriteria correlation，CRITIC）相结合确定指标权重，将權重用于多维云模型中构造岩爆预测模型并应用于工程中;刘磊磊等[16]采用均衡函数优化1～9标度层次分析法获得权重，结合靶心贴近度方法用于工程中岩爆预测;李亚阁等[17]采用1～9标度层次分析法与模糊综合评价法结合建立岩爆预测模型，总结了一种有效的岩爆预测模型。层次分析法主要用于预测指标权重的确定，现有研究在层次分析法的应用上多选用1～9标度法构建比较矩阵[9-17]，在应用过程中需要进行较大的矩阵运算，岩爆的发生是一个复杂的过程，需要综合考虑用于预测的各种因素，得到的预测结果才会更可靠，在应用中如果将预测指标数量扩大化，势必会造成模型的不实用性，选用3标度法构建比较矩阵可以减少权重计算量，很好地弥补了指标数量多造成的计算量大的问题。此外，相对于1～9标度法，3标度法的使用减少了评价过程中的主观性、模糊性。

自熊孝波等[18]首次将物元可拓模型应用于岩爆的预测中来，国内外学者后续对岩爆的物元可拓模型做了相关研究：CHEN等[19]应用变权物元可拓模型对国内外经典岩爆案例进行预测，并与云模型、集对理论模型和功效系数法对比，预测效果更佳;尹彬等[20]采用非对称贴近度替换物元可拓模型评价中的最大隶属度原则，将物元可拓模型应用于西藏甲玛铜矿取得了良好效果;郭生茂等[21]采用熵权法确定物元可拓模型所用权重，将物元可拓模型应用于指导厂坝铅锌矿的岩爆防治。现有的岩爆物元可拓模型多是针对其建模过程中所需权重进行分析与改进，但物元可拓模型本身存在特征值超出节域时关联函数失效的问题[3]，现有研究中少有人对其改进。本文采用无量纲化方法对其改进，改进原理在于无量纲化方法可以将物元可拓模型所需元素归一化到固定区间，通过对建模所需元素的范围确定，从而确保特征值不会超出节域，保证物元可拓模型的普遍可用性。

综述所述，本文选用无量纲化方法改进物元可拓模型，采用3标度法确定物元可拓模型所需的指标权重，建立了改进层次分析-物元可拓的岩爆预测模型，该模型简化了用于传统权重确定的计算量，且采用无量纲化方法对传统物元可拓模型本身存在特征值超出节域时关联函数失效的问题进行了改进。将建好的模型对白鹤滩水电站地下隧洞的岩爆进行预测，获取一种地下工程中岩爆灾害的预测问题的新方法。

1 原理

1.1 层次分析法

层次分析法[22]（analytic hierarchy process，AHP）是一种多指标权重确定的方法，确定指标权重分四步走：构建递阶层次结构、建立判断矩阵、对判断矩阵进行一致性检验和指标权重确定。

首先，确定递阶层次结构。按照参考文献[10]中，选择三层的递阶层次结构，其示意图如图1所示。

其次，建立判断矩阵。本文中对应为目标层A与准则层B之间判断矩阵描述为表1。

1.2物元可拓模型

物元可拓模型[24]是一种全局性最佳决策目标的综合评价模型，主要步骤如下：

（1）确定岩爆危险等级评价指标体系

（2）确定经典域R

假设岩爆危险等级分为z个等级，评价指标有n个，则经典域物元可描述为式（5）：

（3）确定节域R

取各指标在z个岩爆等级中所对应取值范围中的最小值和最大值，构成节域物元，整理于式（6）：

（4）确定待评岩爆物元R

假设待评价的岩爆有m个，那么第i条待评岩爆物元为式（7）：

（5）无量纲化

对传统的物元可拓模型而言，确定完经典域、节域、待评岩爆物元后即可进行建模评测，但这样的模型一般应用于待评物元特征值在节域范围内的指标，一旦评物元特征值超出节域时，会造成关联函数失效，进而导致无法做出预测。针对这一问题，本文参考前人研究成果，对经典域、节域、待评岩爆物元做无量纲化处理，见公式（8）与（9）：

（6）计算岩爆烈度等级评价指标的关联度

第i个岩爆第k个指标关于岩爆烈度等级j的关联函数为式（10）、（11）和（12）：

2工程实例分析

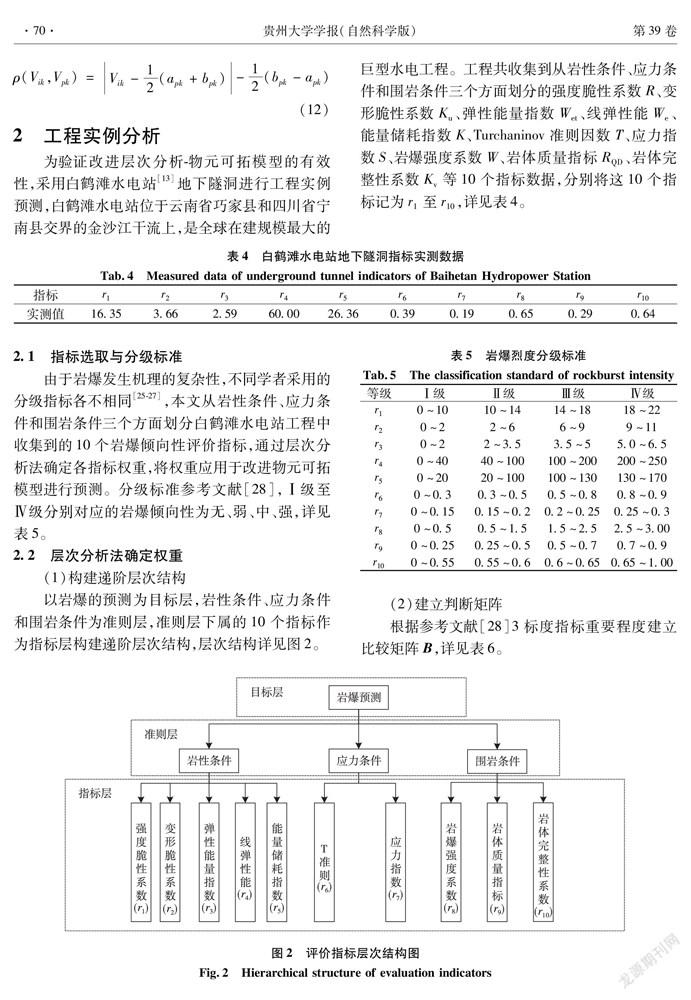
为验证改进层次分析-物元可拓模型的有效性，采用白鹤滩水电站[13]地下隧洞进行工程实例预测，白鹤滩水电站位于云南省巧家县和四川省宁南县交界的金沙江干流上，是全球在建规模最大的巨型水电工程。工程共收集到从岩性条件、应力条件和围岩条件三个方面划分的强度脆性系数R、变形脆性系数K、弹性能量指数W、线弹性能W、能量储耗指数K、Turchaninov准则因数T、应力指数S、岩爆强度系数W、岩体质量指标R、岩体完整性系数K等10个指标数据，分别将这10个指标记为r至r，详见表4。

2.1指标选取与分级标准

由于岩爆发生机理的复杂性，不同学者采用的分级指标各不相同[25-27]，本文从岩性条件、应力条件和围岩条件三个方面划分白鹤滩水电站工程中收集到的10个岩爆倾向性评价指标，通过层次分析法确定各指标权重，将权重应用于改进物元可拓模型进行预测。分级标准参考文献[28]，Ⅰ级至 Ⅳ级分别对应的岩爆倾向性为无、弱、中、强，详见表5。

2.2层次分析法确定权重

（1）构建递阶层次结构

以岩爆的预测为目标层，岩性条件、应力条件和围岩条件为准则层，准则层下属的10个指标作为指标层构建递阶层次结构，层次结构详见图2。

（2）建立判断矩阵

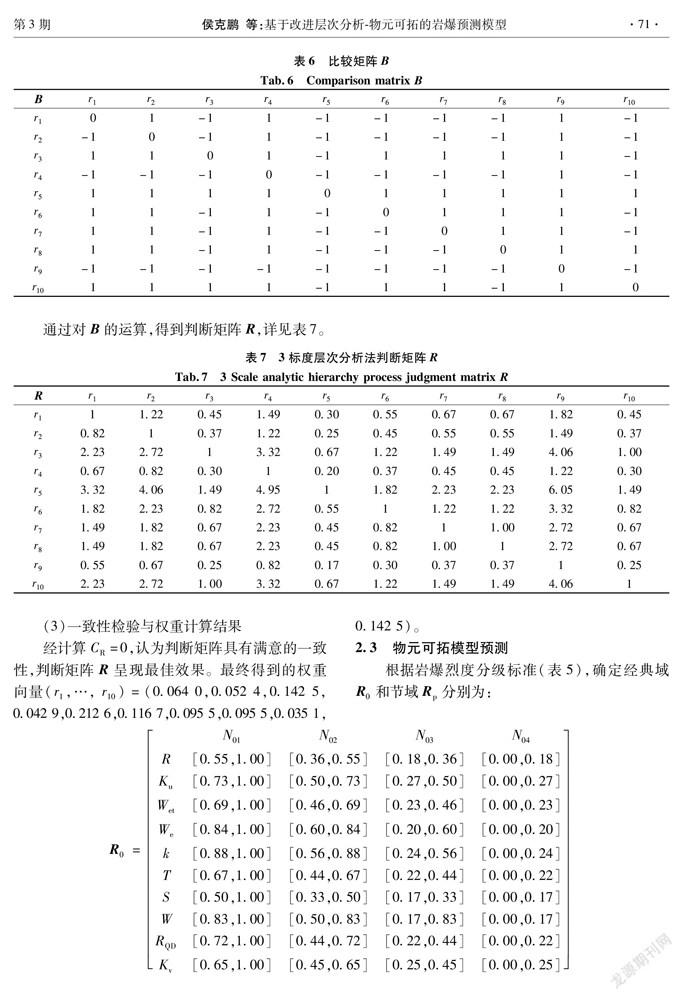
根据参考文献[28]3标度指标重要程度建立比较矩阵B，详见表6。

通过对B的运算，得到判断矩阵R，详见表7。

（3）一致性检验与权重计算结果

2.3物元可拓模型预测

根据岩爆烈度分级标准（表5），确定经典域R和节域R分别为：

依据式（9）和（10）对表5中工程实测数据进行无量纲化处理，最终计算工程数据的岩爆烈度等级关联度，计算得到Ⅰ级关联度为-0.253 5，Ⅱ级关联度为0.153 1，Ⅲ级关联度为-0.221 6，Ⅳ级关联度为-0.521 2，详见表8。

由表8可知，本文模型预测的四个等级关联度中，Ⅱ级的关联度最大（0.153 1），根据最大关联度识别准则，本文预测的白鹤滩水电站样本岩爆情况为Ⅱ级，即弱岩爆。

经对比[13]，该结果与实际情况完全一致。可以说明该模型预测准确，是一种工程应用价值较大模型，可以作为现场经验判断的一种补充。

3结论

1）从岩性条件、应力条件和围岩条件三个方面划分白鹤滩水电站工程中收集到的10个岩爆倾向性评价指标，采用3标度理论构建改进的层次分析法，确定各预测指标的权重向量（R，…，Kv）=（0.064 0，0.052 4，0.142 5，0.042 9，0.212 6，0.116 7，0.095 5，0.095 5，0.035 1，0.142 5）。

2）对物元可拓模型的经典域、节域、待评岩爆物元进行无量纲化处理，将节域中的值控制在0～1之间，从而改进物元可拓模型，结合基于3标度理论的层次分析法，建立改进的层次分析-物元可拓模型，计算白鹤滩水电站工程实例的岩爆烈度等级关联度，计算得到Ⅰ级关联度为-0.253 5，Ⅱ级关联度为0.153 1，Ⅲ级关联度为-0.221 6，Ⅳ级关联度为-0.521 2。

3）采用最大关联度识别准则预测工程实例岩爆烈度，预测样本岩爆情况为Ⅱ级，即弱岩爆，与实际等级一致，是一种具有实践参考价值的岩爆烈度分级模型。参考文献：

[1]钱七虎. 岩爆、冲击地压的定义、机制、分类及其定量预测模型[J]. 巖土力学， 2014， 35（1）： 1-6.

[2] 景杨凡， 陈玉明， 李岳峰， 等. 基于判别分析法的岩爆烈度预测研究[J]. 有色金属（矿山部分）， 2022， 74（1）： 97-102.

[3] 胡建华， 尚俊龙， 周科平. 岩爆烈度预测的改进物元可拓模型与实例分析[J]. 中国有色金属学报， 2013， 23（2）： 495-502.

[4] 龚剑， 胡乃联， 崔翔， 等. 基于AHP-TOPSIS评判模型的岩爆倾向性预测[J]. 岩石力学与工程学报， 2014， 33（7）： 1442-1448.

[5] 王超， 李岳峰， 张成良. 基于大样本数据挖掘分析的岩爆烈度分级预测模型[J]. 昆明理工大学学报（自然科学版）， 2020， 45（1）： 26-31.

[6] 王超， 李岳峰， 邵琳， 等. 基于9种无约束优化算法的岩爆预测BP模型优选[J]. 昆明理工大学学报（自然科学版）， 2021， 46（5）： 32-37.

[7] LI Y F， WANG C， XU J K， et. al. Rockburst prediction based on the KPCA-APSO-SVM model and its engineering application[J]. Shock and Vibration， 2021， 1（1）： 1-12.

[8] 吴顺川， 张晨曦， 成子桥. 基于PCA-PNN原理的岩爆烈度分级预测方法[J]. 煤炭学报， 2019， 44（9）： 2767-2776.

[9] 徐琛， 刘晓丽， 王恩志， 等. 基于组合权重-理想点法的应变型岩爆五因素预测分级[J]. 岩土工程学报， 2017， 39（12）： 2245-2252.

[10]卢富然， 陈建宏. 基于AHP和熵权TOPSIS模型的岩爆预测方法[J]. 黄金科学技术， 2018， 26（3）： 365-371.

[11]石曉燕， 范俊奇， 郭鹏， 等. 深地下工程岩爆影响因素的模糊层次综合分析及评价[J]. 防护工程， 2021， 43（4）： 37-42.

[12]董源， 张引， 习朝辉. 基于组合赋权-TOPSIS理论的岩爆预测研究[J]. 人民珠江， 2018， 39（9）： 87-91.

[13]董源， 裴向军， 张引， 等. 基于组合赋权-云模型理论的岩爆预测研究[J]. 地下空间与工程学报， 2018， 14（S1）： 409-415.

[14]殷欣， 刘泉声， 王心语， 等. 基于组合赋权和属性区间识别理论的岩爆烈度分级预测模型[J]. 煤炭学报， 2020， 45（11）： 3772-3780.

[15]刘晓悦， 杨伟， 张雪梅. 基于改进层次法与CRITIC法的多维云模型岩爆预测[J]. 湖南大学学报（自然科学版）， 2021， 48（2）： 118-124.

[16]刘磊磊， 张绍和， 王晓密， 等. 变权靶心贴近度在岩爆烈度预测中的应用[J]. 爆炸与冲击， 2015， 35（1）： 43-50.

[17]李亚阁， 章光， 焦文宇. 基于模糊层次分析法的岩爆预测研究[J]. 山西建筑， 2008（2）： 108-109.

[18]熊孝波， 桂国庆， 许建聪， 等. 可拓工程方法在地下工程岩爆预测中的应用[J]. 解放军理工大学学报（自然科学版）， 2007（6）： 695-701.

[19]CHEN J H， CHEN Y， YANG S， et. al. A prediction model on rockburst intensity grade based on variable weight and matter-element extension[J]. PLOS ONE， 2019， 14（6）： 1145-1152.

[20]尹彬， 陆卫东， 贾宝山， 等. 岩爆危险性评价的变权物元可拓模型[J]. 金属矿山， 2017（5）： 54-59.

[21]郭生茂， 刘涛， 赵丽军， 等. 熵权物元可拓模型在岩爆危险性等级评价中的应用[J]. 有色金属（矿山部分）， 2015， 67（4）： 89-93.

[22]徐建华. 现代地理学中的数学方法[M]. 2版. 北京： 高等教育出版社， 2004.

[23]杜栋， 庞庆华， 吴炎. 现代综合评价方法与案例精选[M]. 2版. 北京： 清华大学出版社， 2008.

[24]蔡 文， 杨春燕， 林伟初. 可拓工程方法[M]. 北京：科学出版社， 1997.

[25]陈秀铜， 李璐. 基于 AHP-FUZZY 方法的隧道岩爆预测[J]. 煤炭学报， 2008， 33（11）：  1230-1234.

[26]田睿， 孟海东， 陈世江， 等. 基于深度神经网络的岩爆烈度分级预测[J]. 煤炭学报， 2020， 45（S1）： 191-201.

[27]汤志立， 王雪， 徐千军. 基于过采样和客观赋权法的岩爆预测[J]. 清华大学学报（自然科学版）， 2021， 61（6）： 543-555.

[28]关贤欢， 郑相悦， 荣帅. 基于改进层次分析法-云模型的岩爆烈度等级预测[J]. 化工矿物与加工， 2018， 47（8）： 43-47， 55.

（责任编辑：于慧梅）

Based on Improved AHP-Matter-Element Extension

of Rockburst Prediction Model

HOU Kepeng SHAO Lin LI Yuefeng QIAO Mu WANG Tuanhui

（1.Faculty of Land Resource Engineering， Kunming University of Science and Technology， Kunming 650093， China;

2.Yunnan Key Laboratory of Sino-German Blue Mining and Utilization of Special Underground Space， Kunming 650093， China）Abstract： Mathematical modeling method is commonly used in the prevention and prediction of rockbursts， the tricky geological disasters in geotechnical engineering. Combined with the analytic hierarchy process （AHP） and the theory of matter-element extension model， the new model was established to predict rockbursts in engineering. The advantages of the new model are as follows： the analytic hierarchy process （AHP） is improved， using the smaller amount of calculation; the matter-element extension model is improved to avoid the problem of correlation function failure when the eigenvalue exceeds the node domain. The new model， applied to the rockburst prediction of Baihetan Hydropower station， showing good consistency between the actual observation and the prediction， is proved to be reliable and practical in rockburst prediction.

Key words： analytic hierarchy process; matter-element extension model; classification forecasting; engineering application