新工科背景下工程数学课程的教学改革
2022-05-09荀燕琴任国凤王爱珍付建梅
荀燕琴,任国凤,王爱珍,付建梅
新工科背景下工程数学课程的教学改革
荀燕琴,任国凤,王爱珍,付建梅
(忻州师范学院 电子信息科学与技术系,山西 忻州 035000)
基于新工科背景对高水平工程人才的培养要求,研究了作为工程基础课程的工程数学的教学改革问题.基于新时期对课程的要求,对课程内容和教学方法进行改革,从新工科培养要求进行教学实例及仿真的融合,根据新工科的内涵引领立德树人,引入学习与思考、辩证发展等思政元素.通过新工科背景下的教学改革,不仅解决了教师教的困难,更解决了学生学的困难的问题,有效提升了学生的理论学习及实践应用能力,使之成为新时期合格的工程技术人才.
工程数学;教学方法;新工科;课程思政
为推动新工程建设及工程教育改革创新,2017年2月以来教育部先后主持开展多场研讨会,形成了“复旦共识”“天大行动”和“北京指南”,并发布了一系列政策文件[1].2018年10月,教育部、工业和信息化部、中国工程院联合发布《关于加快建设发展新工科实施卓越工程师教育培养计划2.0的意见》[2],进一步将新工科建设提到了新高度.
工程数学是工科专业的一门专业基础课程[3],承接于公共基础课程高等数学,扩展至许多专业的专业必修课程,如通信工程专业的信号与系统和数字信号处理,物理专业的电磁场理论、流体力学,自动化专业的自动控制理论[4-5]等.教师应积极进行教学改革,努力提高课堂质量,提升学生的学习创新能力.本文以陆庆乐等编写的教材《工程数学·复变函数》[6]为例阐述相关教学改革问题.
1 课程内容改革
工程数学课程对于工科类专业的重要性显而易见,但是其课程难度也让很多学生望而却步,工程数学一直是挂科率较高的科目之一,学生普遍反映课程难且不容易掌握.随着学院对课程的优化,工程数学的课时数量被削减,如何在有限的课时内实现课程内容有效的讲授,是课程改革所面临的一个难题.
1.1 根据内容侧重点精练课程
在教学过程中要精练课程内容,工程数学是偏重应用的工程类数学,因此在数学中偏重的理论推导在这里可以忽略或者概述.如2.2节中函数解析的充要条件,学习的目的是为了利用定理去判定函数的解析性,因此在这里大篇幅的定理证明过程被忽略,但是在解析性的充分性证明过程中推理出了复变函数的导数公式,因此综合考虑,在讲解此部分内容时,根据函数解析性定义推理证明定理的必要性的过程可以忽略,而充分性的证明则需要详细描述,以此向学生展示导数公式.其他相关内容侧重处理案例见表1.

表1 内容侧重处理案例
通过对课本知识点的详细研究及侧重点处理,可以有效地精练课程内容.
1.2 根据例题梳理章节内容
在授课过程中,有意识地培养学生的总结及思考能力,通过一些例题对一个知识点进行扩张,并且连接相关的知识点,进一步压缩课程,同时提高学生的学习效率.


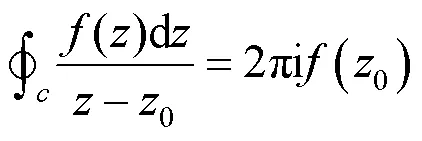
由此可见,在授课过程中可以根据知识点的相关性,进一步梳理知识点,提高授课的效率.
总而言之,教师应根据教学目的,有效处理教学内容,做到有的放矢;根据知识点的融会贯通,处理及总结相关知识点,有效压缩教学内容,同时提高教学效率,满足新时期对课程的优化要求.
2 教学方法及教学手段改革
2.1 教学方法改革
在教学过程中要注重教学方法,在精练课程内容的基础上提高教学效率.在授课过程中可以采用对比法、讨论法、自主学习法等提高教学效率.
在教学过程中通过复变函数和实变函数的对比,可以有效地提高课程的教学效率,相关知识点案例见表2.

表2 复变函数和实变函数相关知识对比
2.2 教学手段改革
工程数学课程的主要特点在于其理论性强、内容抽象、概念定理繁多、各章节的前后联系密切、解题的方法和技巧都有针对性等[7].传统的课堂教学以讲授为主,教与学的过程较为枯燥.传统方法是让学生进行纯粹数学理论知识的学习和训练,相对比较枯燥乏味,学生不容易学,教师不容易教.为了加深学生对所学知识的理解,提高学生的学习兴趣,有必要进行教学改革,充分结合先进技术和仿真工具,开展研究性教学.
2.2.1在理论课程讲授中加入Matlab仿真 在新工科背景下,将Matlab仿真应用于课程教学,可以将数学知识和学生将要学习的专业课程联系起来,提高数学教学的针对性,加深学生对理论及算法的理解,提高其实践能力.在章节的讲解中,通过Matlab的应用,提高学生对课程的兴趣,通过鲜活的实例加深对晦涩的理论知识的掌握.
解求复变函数极限的Matlab程序为:
syms z complex
z0=1+1i*2;
fz=z^2;
Subs(fz,z,z0).
运行结果为:ans=-3+4i.
[R,P,K]=residue([2,-1,1][1,-1])
%R表示留数;P表示极点位置;K表示直接项.
运行结果为:R=2 P=1 K=2.
求积分的Matlab程序为:
W=2*PI*I*2.
运行结果为:W=0+12.57i.
解求Laplace变换的Matlab程序为:
syms t s a b,f=exp((-b)*t)*sin(a*t),F=laplace(f,t,s).
运行结果为:
f=sin(a*t)/exp(-b*t);
F=a/((b+s)^2+a^2).
2.2.2在授课过程中引入应用实践复变函数及积分变换是电子专业的一门学科基础课,后继课程为信号与系统、通信原理等电子专业核心课程.课程开设的目的是深化本专业的数学基础,扩大学生的数学知识面,培养学生的抽象思维能力,提高学生的数学建模能力和解决实际问题的能力,为本专业的后续课程作准备.在授课过程中,通过联系后续课程的实际问题解决,深化学生对工程数学中理论的理解,同时可以提高学生的学习兴趣.
案例1在实际应用中,电路问题等均可建模成常系数微分方程.在求解常系数微分方程时,可以用laplace变换求解方程的系统函数,进而求解系统函数的零极点分布和幅频特性曲线.

图1 系统的零极点分布

图2 系统的幅频和相频特性曲线
案例2在语音信号的处理中可以利用傅氏变换进行信号的分析.通过语音的傅里叶变换,可以将时域信号转换到频域进行分析.
原始语音信号见图3a,经过傅里叶变换之后的频谱见图3b,其表示各频率分量的大小,同时还可以得到语谱图(见图3c),其表示信号频率分量随时间的变化规律,反映了语音信号的动态频谱特性.

图3 语音信号的处理
3 课程思政
思政教育符合新工科背景下的内涵引领,在课程中融入思政教育不仅可以提升学生的学习兴趣,还可以提升学生的思想道德修养[8-9].
3.1 授课中渗透学习和思考的辩证关系
学习与思考、勤学与善思是相互联系和相辅相成的,只有把学习和思考紧密结合起来,才能学到切实有用的知识.孔子曰:“学而不思则罔,思而不学则殆.”这句名言深刻道出了学习与思考的辩证关系,告戒我们学习要防止“学而不思”和“思而不学”这2种现象.学习的过程实际是一个不断思考认知的过程,如果没有思考,再好的知识也难以吸收,正所谓“不深思则不能造于道,不深思而得者,其得易失”.
在复变函数中,复变函数积分和留数定理都是用来求解积分的.对于第三章来说,求解闭合曲线积分有柯西古萨基本定理、柯西积分公式、高阶导数公式,每个公式有各自的使用条件和范围,对于实际复杂积分式,通常不能直接套用某个公式,需要进行思考,选择部分分式或者其它形式化成公式形式,才可以应用.又如留数定理公式,其实质是应用复合闭路定理,相当于第三章的延伸,运用其求解积分只需求出被积函数在奇点处的留数即可.在实际求解中,选择哪种方法去求解,都需要在熟悉理论的基础上勤于思考和总结.
在-函数的引入过程中,根据实际物理现象中在某个瞬间给系统某个输入这种情况建立数学模型,发现实际并不存在这样的函数,因此有了特殊函数即-函数.所学的知识来源于生活,包括牛顿定理的引入也是由于苹果的落地现象,在生活中要善于思考,善于发现问题.同时,-函数的引入对于求解类似问题提供了数学模型,便于类似问题的求解.
在教学过程中,时刻提醒学生要勤于思考,善于发现问题,解决问题,才能学有所成.
3.2 授课过程中渗透辩证发展观念
结合我国实际和时代条件,学习和运用辩证唯物主义世界观和方法论,要学习掌握认识和实践辩证关系的原理,坚持实践第一的观点,不断推进实践基础上的理论创新.因此在课程中可以渗透辩证发展观念,理论实践结合,引导学生进行创新.
案例3在课程中学过fourier变换及其应用,为什么还需要学习Laplace变换?fourier变换和Laplace变换是什么关系?
工程数学相关思政案例见表3.

表3 工程数学中的课程思政
4 结语
新工科是基于国家战略发展新需求、国际竞争新形势、立德树人新要求而提出的我国工程教育改革方向,其内涵是以立德树人为引领,以应对变化、塑造未来为建设理念,以继承与创新、交叉与融合、协调与共享为主要途径,以新理念、新模式培养未来多元化、创新型、具有可持续竞争力的卓越工程人才[10-11].在实际授课中,注意理论与实际的结合可以提升学生的工程处理能力,提高授课效率;同时课程中引入思政元素,提升学生的思想道德修养.
新工科类的高技术人才是时代对当代大学生的要求,复变函数与积分变换课程作为工科课程的基础理论课程,也应该顺应发展趋势,对工程数学教学进行全方位改革,将新工科理念融入课堂教学,真正培养具有科学素养和全面发展的专业型工程类人才,提高时代竞争力.
[1] 蔡敏,张东立.应用型本科高校工程数学课程的教改研究[J].教师,2020(23):58-59.
[2] 宋述芳,吕震宙,张伟伟,等.“新工科”建设背景下工程数学教育改革探索研究[J].科教文汇(上旬刊),2019(6):68-71.
[3] 彭慧春,李继清,宋晓漓.新工科背景下多学科交叉探究式数学教学模式的探讨[J].教育现代化,2018,5(50):169-171.
[4] 王洋,董良杰,于春海.“工程数学”课程的教学改革的研究[J].农业网络信息,2017(8):99-101.
[5] 杨威,高淑萍,陈怀琛,等.新工科背景下线性代数教学改革与探索:以国家精品在线开放课程《实用大众线性代数》为例[J].高教学刊,2020(5):8-12.
[6] 陆庆乐,王绵森.工程数学·复变函数[M].4版.高等教育出版社,1996.
[7] 杨文霞,何朗,刘扬.新工科背景下工程数学课程群教学改革与实践:以武汉理工大学为例[J].大学教育,2020(1):25-27.
[8] 吴旭.新工科建设背景下工程数学教学改革与探索[J].教育教学论坛,2019(30):88-89.
[9] 申立平,吴延红.案例教学法在工程数学课程改革中的研究[J].数学学习与研究,2018(21):27.
[10] 刘三明.将思政教育融入应用工程数学课堂教学中的探索[J].教育教学论坛,2020(22):346-347.
[11] 高明.高等数学课程思政教学探索[J].天津市教科院学报,2019(3):60-66.
Teaching reform of engineering mathematics under the background of new engineering education
XUN Yanqin,REN Guofeng,WANG Aizhen,FU Jianmei
(School ofElectronic Information Science and Technology,Xinzhou Normal University,Xinzhou 035000,China)
Based on the training requirements of the new engineering background for high-level engineering talents, the teaching reform of engineering mathematics as a basic engineering course was studied.Based on the requirements of the course in the new era,reform the course content and teaching methods,integrate the teaching examples and simulation from the training requirements of the new engineering education,guide the establishment of morality and talents according to the connotation of the new engineering education,and introduce the ideological and political elements of learning and thinking,dialectical development and so on.Through the teaching reform under the background of new engineering education,it can not only solve the difficulties of teachers′ teaching,but also solve the difficulties of students′ learning,effectively improve students′ abilities of theoretical learning and practical application,enable students to become qualified engineering and technical talents in the new era.
engineering mathematics;teaching method;new engineering education;curriculum thought and politics
1007-9831(2022)04-0070-06
O174.5∶G642.0
A
10.3969/j.issn.1007-9831.2022.04.014
2021-10-19
忻州师范学院教学改革创新项目(JGYB202006);山西省高等学校教学改革创新项目(J2021572)
荀燕琴(1988-),女,山西临汾人,讲师,硕士,从事信号处理、智能算法研究.E-mail:361942664@qq.com
