基于SEIR模型的COVID-19传染力研究

马思婕，黄珈铭，印英东，曾楚仪

（广州大学数学与信息科学学院，广东 广州 510006）

0 引言

2019年末，新冠突袭无疑是人类史上的一大灾难，短短几日便让人们看到了它的“威力”。2020年3月11日，世卫组织将新冠肺炎疫情认定为全球大流行。实际上，全球大流行并不是第一次出现，西班牙流感、H1N1猪流感、西非埃博拉疫情……这也侧面告诉人们：在以往经历中吸取经验，寻求合适的预测模型进行科学防疫尤为重要。

在疫情早期便有许多学者开始了与COVID-19相关的研究，不过早期的数据、现象还不够成熟，过早过快地下结论会造成较大偏差。本文在相对成熟的数据及现象下进行了分析预测，对疫情走势进行有效预测及传染力判断，希望通过对COVID-19的研究，得到较成熟的模型，为日后类似突发情况提供帮助。

1 模型建立

1.1 人群流动分析

在考虑居家隔离、医学隔离、入院治疗等防疫政策和医学干预的情况下，本文对各舱室人群的流动情况进行了分析（见图1）。

图1 人群流动变化

在模型建立的过程中，为了排除其他因素干扰，将不考虑非COVID-19所引起的人口变化，如自然死亡等。在将模型实践到具体地区时，假设该地区在所研究时间段内人口恒定，系统内各类人口总和不发生改变。浦江创新论坛系列活动“特别对话：科技创新与全球健康共治”［1］中，复旦大学附属华山医院感染科主任张文宏表示：在现实中存在复阳、二次感染情况，但属于极小概率事件，故在模型中将不考虑二次感染情况，即被感染者人群痊愈后归入康复者类中，不再流动转变。

1.2 各类人群关联性的微分方程建立

根据1.1中各类人群的流动分析，可建立如下各类人群关联性的微分方程：

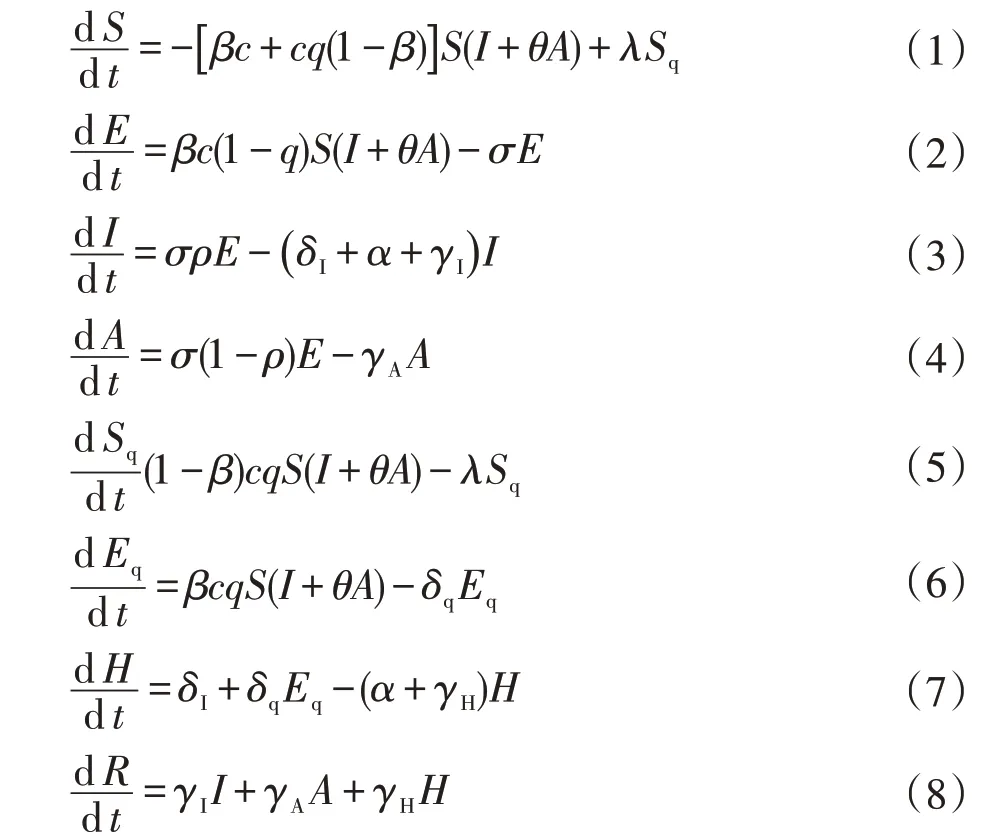
该模型中引进了一些参数以表现群体的变化流动。式中：c代表一个暴露的具有感染力的患者的接触率；β代表每次接触的传播概率；q代表接触者被追踪到隔离的概率；σ代表受感染个体转向受感染类的转化率；λ代表隔离的未感染接触者被释放到更广泛的社区的速度；δI代表有症状的感染者转变为住院患者的比率；δq代表隔离易感人群转变为住院患者的比率；θ代表无症状感染者相对于有症状感染者传播力的比值；γI代表未住院有症状感染者的康复率；γA代表无症状感染者的康复率；γH代表住院患者的康复率；α代表死亡率。

2 模型求解

本文分别以北京市总人口、武汉市总人口为初始易感人群作为研究对象，通过北京市卫生健康委员会网站［2］、湖北省卫生健康委员会网站［3］公开发布的官方数据为原始数据，收集2020年1月23日—3月17日的疫情信息并对所获得的数据进行处理与筛选。数据处理与筛选后出现数据缺失的情况，因此在得到正确的实验数据前本文进行了数据的缺失度检验，发现数据缺失度为1.37%，缺失度较低。经分析可知缺失部分为MAR随机缺失，可直接选用模型方法对数据进行填补。对于处理后得到的理想数据进行去噪处理与汇总，得到两城市较准确的COVID-19感染人数变化数据，为本文模型的训练预测拟合提供重要基础。

2.1 参数估计相关计算

（1）由疫情防控指南了解到［4］，一般隔离周期为14 d，故可得到隔离的未感染接触者被释放到更广泛社区的速度λ=1/14。

（2）由世卫组织的相关研究［4］可知，COVID-19的平均潜伏期为7 d，故可得到受感染个体转向受感染类的转化率σ=1/7。

（3）其他参数的估测方法。对于SEIR模型中的参数估计，本文采用基于分支过程的Monte-Carlo算法［5］，通过建立随机并基于分支过程描述COVID-19的传播过程（见图2），从而对数据进行预测（见表1）。

表1 参数的计算估计取值

图2 分支过程

根据分支过程理论，病毒传播过程中人与人接触产生的传播是随机独立的。对这种大量随机行为的描述符合计算机Monte-Carlo算法的应用要求。

本文以收集到感染人数数据的前80%作为训练集拟合目标函数，后20%作为参数估计集用于优化函数中的参数取值。为了增强算法应用的准确性，本文在执行模型的过程中，不断调整步长以求得较优的参数取值。对实际数值和模拟数值用最小二乘法衡量其相似程度，不断优化参数取值。由多种参数的取值并兼顾疫情发展带来的参数变化，进行疫情发展过程模拟。模拟结果与实际数据进行对比，发现模拟的贴合度达到91.49%，有理由认为算法拟合出的模拟情况从概率意义上表明了未来实际疫情的发展趋势。

2.2 基本再生数R0的计算结果

由于疫情暴发中经历了医疗资源不足以及相关隔离政策颁布的过程，因此COVID-19传播前期的R0与传播后期的R0有较大区别［6］。根据现实情况可知，由于医疗资源供应在2020年2月13日左右充足，因此本文以2020年2月13日为分界点，对两城市的R0进行前期和后期计算，得到结果，如表2所示。

表2 R0分界计算结果

2.3 基于模型的感染者数据走势预测

通过上文中相关参数的估计，对后续感染者的数据走势进行了预测，预测情况，如图3所示。

图3 预计累计感染人数与实际情况比对

3 灵敏度分析

为研究本模型是否能较为灵敏地进行预测，且误差是否会对模型结果造成显著影响，本文通过改动在SEIR模型中对传染影响较大的两个参数c，q，以观察最终拟合曲线的改变情况，结果如图4所示。

图4 基于参数c，q的模型灵敏度分析

改动参数c，即暴露的具有感染力的患者的接触率发生了改变，这是对疫情下防疫政策的直观体现。观察图4可以看到，模型预测的累计感染人数产生较大波动，但参数变化造成的预测值变化在合理范围内。表明本模型在进行预测时对于参数c的变动感应较为灵敏，可以依据不同的防疫政策、措施进行合理预测，适用度较广泛。

同时，本文在保持c取值为14.8的情况下，对参数q进行灵敏度分析。

改动参数q，即接触者被追踪到隔离的概率，这是对防疫体系成熟与否的直观鉴定，相对成熟的防疫体系下，参数q自然相对较高，反之则较低。观察图4可以看到，改变参数q的值，参数变化造成的预测值变化在合理范围内。表明本模型在进行预测时对于参数q的变动感应较灵敏，再次验证本模型可以为不同的情境、防疫体系进行合理预测。

综上可知，在不同病毒、不同的防疫防护政策下，模型反应灵敏，具有时效性，可为不同类型传染性病毒、不同地区及国家不同的防疫政策、措施提供模型基础。

4 结语

针对COVID的传染力研究，本文建立了改进的SEIR病毒模型，并且以医疗资源以及相关隔离政策颁布情况前后进行分析。以2020年2月13号作为分界日期，2月13号之前为前期，之后为后期，将模型实践到北京市及武汉市，得到北京市前期基本再生数R0=2.135 0、北京市后期R0=1.973 0；武汉市前期R0=3.127 0、武汉市后期R0=2.429 0。同时，本文研究结果表明，北京市的疫情高潮会在2020年2月3日左右到来，武汉市的疫情高潮将会在2020年2月6日左右到来，该段时间病毒传播的概率最高，要注意防控，严防严控才能有效降低病毒的传染力。