裂缝-孔隙型碳酸盐岩气藏稳态产能评价方法

刘荣和，张文彪，冷有恒

(1.中国石油川庆钻探工程有限公司，四川 成都 610051；2.中国石油(土库曼斯坦)阿姆河天然气公司，北京 100000)

0 引 言

裂缝-孔隙型碳酸盐岩储层储集空间类型多样，溶蚀孔洞与裂缝广泛发育，在气藏开发过程中形成2套渗流场，介质间流体窜流相互耦合，使得气藏产能受到诸多因素影响，若直接采用常规气藏产能方程进行评价，其结果与实际情况差异较大，因此，有必要开展裂缝-孔隙型碳酸盐岩气藏稳态产能评价方法研究。

中国学者对垂直裂缝井或压裂井的产能方面做了大量的研究，但对发育天然裂缝的裂缝-孔隙型碳酸盐岩储层产能研究相对较少[1-7]。王子胜等[8]建立了双重孔隙压敏介质油藏不稳态产能模型，分析了应力敏感系数、窜流系数、裂缝储容比及表皮系数对不稳态产能的影响；朱斌等[9]通过建立和求解裂缝-孔隙型两区复合地层定井底流压生产数学模型，分析了不同储容比、窜流系数、近井区渗透率、污染半径下的产量随时间变化特征；刘德华[10]将裂缝-孔隙型储层等效为2个均质圆环地层，建立了裂缝-孔隙型介质储层产能计算模型，分析了基岩渗透率、裂缝渗透率及裂缝供给半径对米采油指数的影响；冯金德等[11]采用等值渗流阻力法建立了裂缝型低渗透油藏稳态渗流的理论模型，研究了天然裂缝参数对产量及压力的影响规律；杨济源等[12]采用马丢函数计算了椭圆坐标系中的气体渗流微分方程，求出双重介质气藏非稳态产能表达式，讨论了表皮系数、渗透率各向异性、弹性储容比等参数对不稳态产能曲线的影响；商克俭等[13]则采用数值模拟分析了窜流强度、高速非达西效应、应力敏感及滑脱效应对裂缝-孔隙型双重介质生产的影响。但上述研究并没有考虑天然裂缝参数对气藏稳态产能的影响，为此，该文利用Kazemi模型对裂缝-孔隙型碳酸盐岩气藏进行简化，将双重介质复杂渗流问题分解为基质层线性渗流与水平裂缝径向渗流问题，基于双重介质稳态流动，建立了综合考虑裂缝渗透率、裂缝开度、裂缝条数及窜流系数的裂缝-孔隙型碳酸盐岩气藏稳态产能模型，对气井稳态产能进行敏感性分析。研究成果对深入认识双重介质碳酸盐岩气藏的生产动态具有重要意义。

1 模型假设及渗流特征描述

在裂缝-孔隙型碳酸盐岩气藏的实际地层中，裂缝分布杂乱且无规律，直接研究其稳态产能特征相当困难。为了研究方便，采用Kazemi模型将裂缝-孔隙型地层简化为由水平裂缝和水平基质层相间组成的地层(图1)。

针对Kazemi模型做出如下假设：①地层为水平、均质、各向同性的立方体，长、宽均为L，厚度为h；②地层被N条水平裂缝分割成厚度均等的基质层，裂缝开度为e，基质层厚度为h/N；③基质层与水平裂缝为2套不同的渗流系统，各系统内地层压力相同且同步下降；④气井位于立方体地层中心，气体为弱可压缩的牛顿流体；⑤气体等温渗流，无任何特殊的物理化学现象发生；⑥气体遵循达西渗流规律，忽略重力与毛管力。

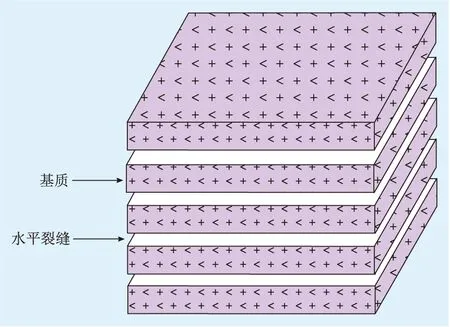
图1 Kazemi模型Fig.1 The Kazemi model

假定Kazemi模型为双孔单渗模型，渗流过程依次分为3个阶段：第1阶段为水平裂缝系统向井筒流动阶段；第2阶段为基质层系统向水平裂缝系统窜流阶段，窜流量等于水平裂缝系统向井筒的流入量；第3阶段为基质层系统向水平裂缝系统拟稳态流动阶段。在此认识基础上，开展裂缝-孔隙型碳酸盐岩气藏稳态产能方程研究。

2 裂缝-孔隙型碳酸盐岩气藏稳态产能计算公式

在Kazemi模型中，1个基质层向2条水平裂缝窜流，每条水平裂缝获得该基质层1/2窜流量，同时1条水平裂缝接受2个基质层向其窜流，即1条水平裂缝获得的流量等于1个基质层流出的流量。因此，在建立裂缝-孔隙型碳酸盐岩气藏稳态产能模型时，将1个基质层与1条水平裂缝构建为1个单元体来进行研究。

2.1 基质层向水平裂缝窜流

假设基质层中的流体都集中在基质层的中线位置，从该位置向基质层与水平裂缝的接触面流动(图2)，流体流动符合线性渗流规律，不考虑气体紊流；图2中红色箭头表示流体流动方向。

图2 1个基质层内流体向1条水平裂缝线性窜流示意图Fig.2 The schematic diagram of linear channeling of fluid in a substrate layer to a horizontal fracture

基质层向水平裂缝线性窜流的运动方程为：

(1)

式中：νm为基质层中的气体渗流速度，10-6m/s ；α为地层形状因子；Km为基质层的渗透率，mD；μ为气体黏度，mPa·s；dp/dx为基质层中的压力梯度，MPa/m。

根据真实气体状态方程，得到气体的密度为：

(2)

式中：ρg为气体的密度，kg/m3；ρgsc为气体在标准状态下的密度，kg/m3；psc为标准状态压力，MPa；Tsc为标准状态温度，K；Zsc为标准状态下的气体偏差因子；p为气体压力，MPa ；T为气体温度，K；Z为气体偏差因子。

根据渗流速度的定义，基质层中的气体渗流速度νm又可写成：

(3)

式中：qscr1为一个基质层向一条水平裂缝线性渗流的窜流量，10-6m3/s；A为线性渗流的截面积，m2；L为气藏立方体地层边长，m。

将式(2)代入式(3)，再将式(3)代入式(1)，可得：

(4)

对式(4)两端积分：

(5)

式中：pm为基质层的地层压力，MPa；pf为水平裂缝的地层压力，MPa；h为气藏地层厚度，m；N为地层中水平裂缝条数；h/2N为气体从基质层的中线位置流到裂缝接触面的距离，m；x为基质层中流体的流动距离，m。

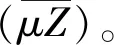
(6)

2.2 水平裂缝向井筒流动

不考虑气体紊流，水平裂缝中的流体向位于中心的井筒做径向流动，当立方体地层边长足够大时，流动范围可等效为半径为L/2的内切圆(图3)，图3中红色箭头表示流体流线及其流动方向。

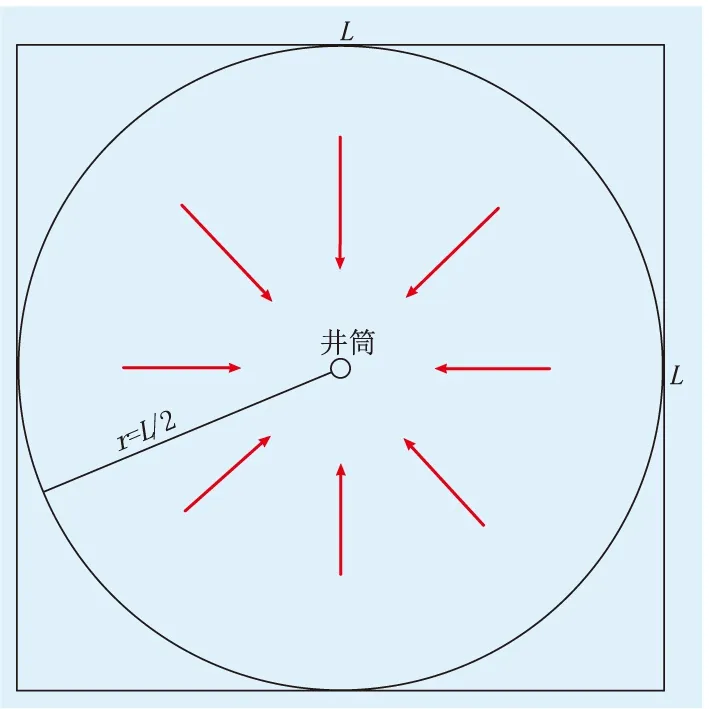
图3 1条水平裂缝内流体向井筒径向流动示意图Fig.3 The schematic diagram of fluid radial flow in a horizontal fracture to wellbore

气体在水平裂缝中的径向流运动方程为：

(7)

式中：νf为水平裂缝中的气体渗流速度，10-6m/s ；Kf为水平裂缝渗透率，mD；dp/dr为水平裂缝中的压力梯度，MPa/m。

根据渗流速度定义，水平裂缝中的气体渗流速度νf又可写成：

(8)

式中：qscr2为1条水平裂缝向井筒流动的流入量，10-6m3/s；e为水平裂缝开度，m；r为气体在水平裂缝中的流动半径，m。

将式(2)代入式(8)，再将式(8)代入式(7)，整理得到：

(9)

对式(9)两端积分，可得1条水平裂缝向井筒径向流动的流入量为：

(10)

式中：pwf为井底流动压力，MPa；rw为井筒半径，m。

2.3 裂缝-孔隙型气藏稳态流动

当裂缝-孔隙型气藏稳态流动时，1个基质层向1条水平裂缝线性渗流的窜流量等于1条水平裂缝向井筒径向流动的流入量，则：

(11)

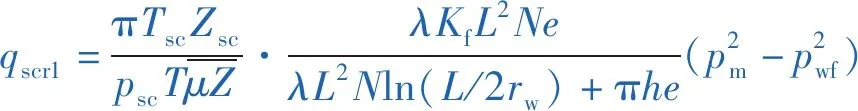
(12)

式(12)即为考虑了裂缝渗透率、裂缝开度、裂缝条数及窜流系数的单元体稳态产能方程。当裂缝-孔隙型碳酸盐岩气藏中存在N条裂缝时，其稳态产能方程可表示为：

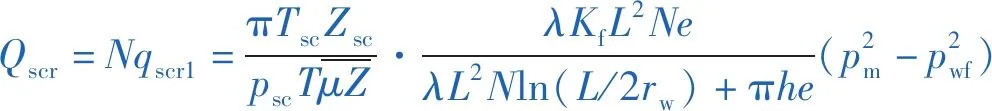
(13)

式中：Qscr为裂缝-孔隙型碳酸盐岩气藏存在N条裂缝时的产气量，10-6m3/s。

3 实例应用

3.1 实例计算

以土库曼斯坦CH裂缝-孔隙型碳酸盐岩气藏为例，气藏地层温度为390 K，气体相对密度为0.65，平均黏度为0.028 2 mPa·s，平均偏差因子为1.169 4，井筒半径为0.1 m；其他基本参数见表1、2。

根据表1、2中数据，采用稳态产能模型计算4口气井无阻流量并与实测数据无阻流量对比，两者相对误差在±5.0%以内(表3)，证明了稳态产能模型的可靠性。

表1 CH气藏气井其他基本参数Table 1 The list of other basic parameters of gas wells in CH gas reservoirs

表2 CH气藏气井系统测试数据统计Table 2 The statistics of system test data for gas wells in CH gas reservoirs

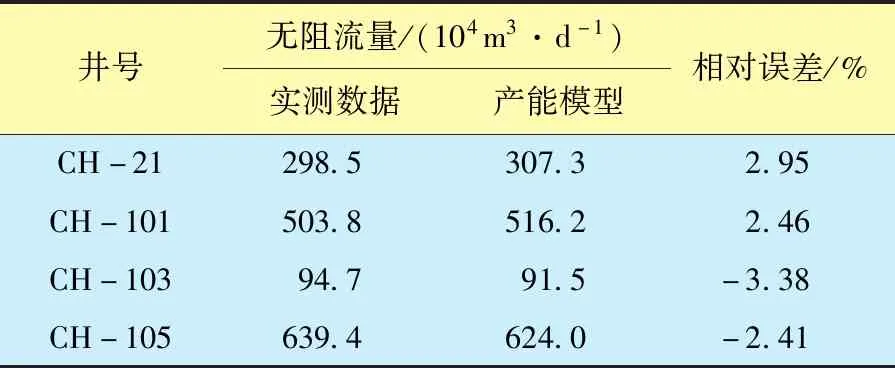
表3 CH气藏气井产能实测无阻流量与产能模型无阻流量对比Table 3 The comparison of measured open-flow capacity of gas wells in CH gas reservoirs with the open-flow capacity of the productivity model

3.2 影响因素分析

3.2.1 裂缝渗透率对产能的影响

以CH-21井为例，保持其他参数不变，绘制裂缝渗透率分别为0.25、0.50、1.00、2.00、4.00 D的裂缝-孔隙型气藏气井IPR曲线(图4)。由图4可知：裂缝渗透率对气井产能影响显著，裂缝渗透率越大，气井无阻流量越大；当裂缝渗透率由0.25 D增至0.50、1.00、2.00、4.00 D时，气井无阻流量分别提高了1、3、7、15倍，两者表现出正相关。

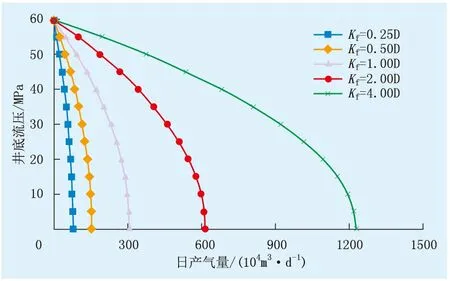
图4 裂缝-孔隙型气井不同裂缝渗透率下流压与日产气量关系Fig.4 The relationship between flow pressure and daily gas production in fractured-porous gas wells with different fracture permeabilities

3.2.2 裂缝开度对产能的影响

以CH-21井为例，保持其他参数不变，绘制裂缝开度分别为0.5、0.6、0.7、0.8、0.9 mm的裂缝-孔隙型气藏气井IPR曲线(图5)。由图5可知：裂缝开度对气井产能影响较明显，裂缝开度越大，气井无阻流量也越大；当裂缝开度由0.5 mm分别增至0.6、0.7、0.8、0.9 mm时，气井无阻流量分别提高19.8%、39.5%、59.1%、78.6%，两者表现出正相关。

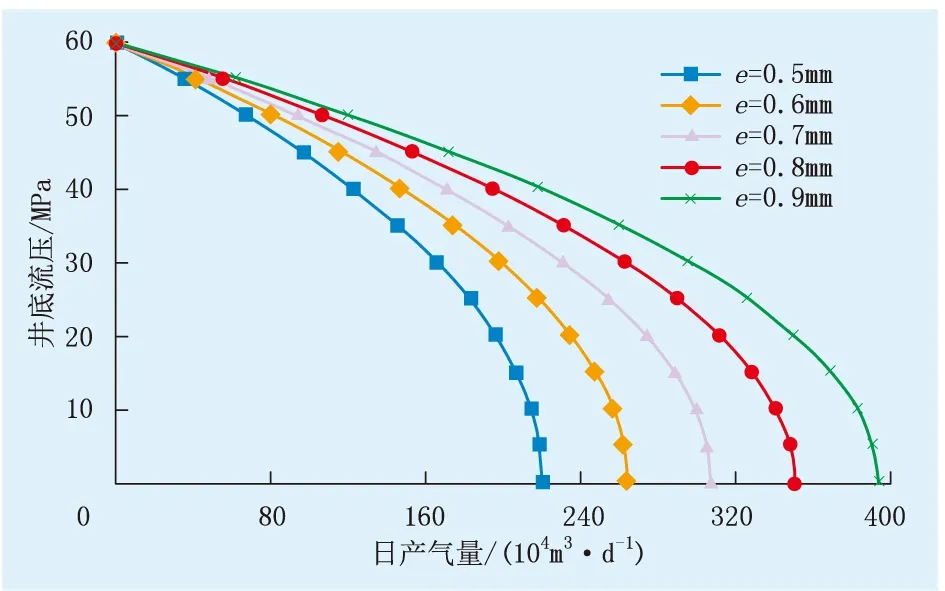
图5 裂缝-孔隙型气井不同裂缝开度下流压与日产气量关系Fig.5 The relationship between flow pressure and daily gas production in fractured-pore gas wells with different fracture openings

3.2.3 裂缝条数对产能的影响

以CH-21井为例，保持其他参数不变，绘制裂缝条数分别为100、150、200、250、300的裂缝-孔隙型气藏气井IPR曲线(图6)。由图6可知：裂缝条数对气井产能影响较为显著，裂缝条数越多，气井无阻流量越大；当裂缝条数由100分别增至150、200、250、300时，气井无阻流量分别提高51.4%、102.7%、154.1%、205.5%，两者表现出正相关。

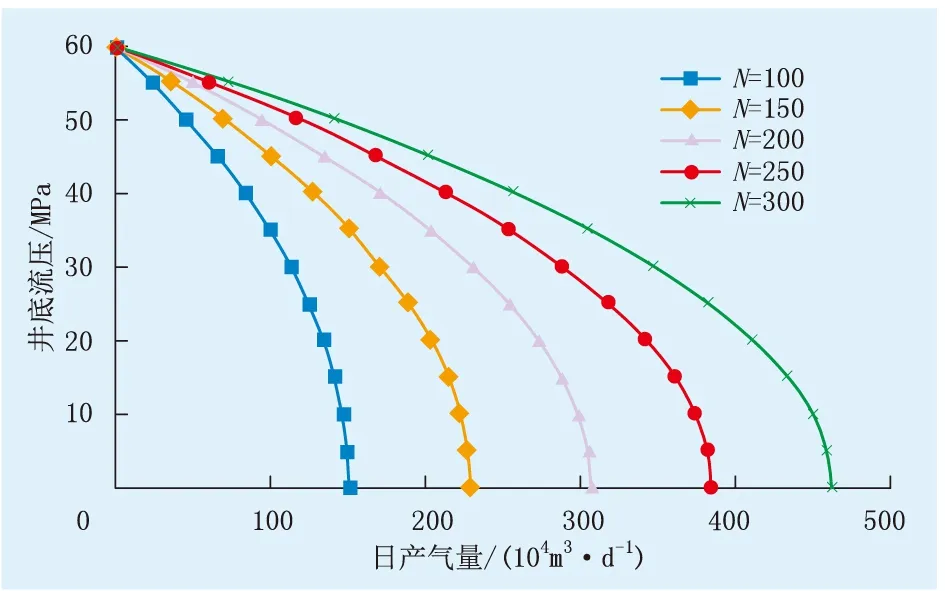
图6 裂缝-孔隙型气井不同裂缝条数下流压与日产气量关系Fig.6 The relationship between flow pressure and daily gas production in fractured-pore gas wells with different number of fractures

3.2.4 窜流系数对产能的影响

以CH-21井为例，保持其他参数不变，绘制窜流系数分别为5×10-12、5×10-11、5×10-10、5×10-9、5×10-8的裂缝-孔隙型气藏气井IPR曲线(图7)。由图7可知，随着窜流系数不断增大，气井无阻流量也随之增加，但其增加程度却逐渐降低；当窜流系数由5×10-12增至5×10-11、5×10-10、5×10-9、5×10-8时，气井无阻流量分别提高109.6%、135.4%、138.4%、138.4%，这表明窜流系数大于5×10-9时，气井无阻流量基本不再受窜流系数变化影响。

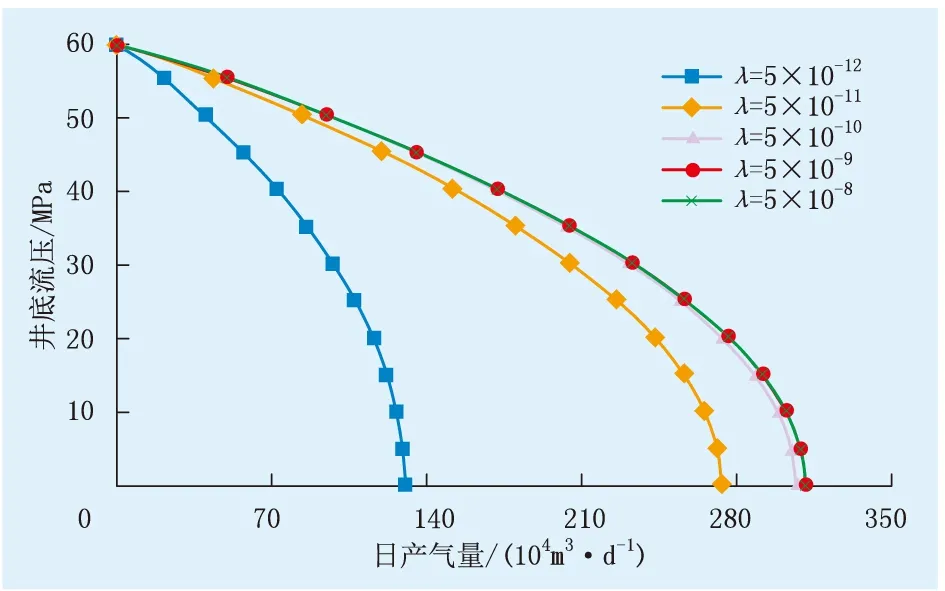
图7 裂缝-孔隙型气井不同窜流系数下流压与日产气量关系Fig.7 The curve of flow pressure and daily gas production in fractured-porous gas wells with different channeling coefficients

4 结 论

(1)利用Kazemi模型对裂缝-孔隙型碳酸盐岩油藏模型进行简化，将双重介质的复杂渗流问题分解为基质层线性渗流与水平裂缝径向流问题，建立了综合考虑裂缝渗透率、裂缝开度、裂缝条数及窜流系数的裂缝-孔隙型碳酸盐岩气藏稳态产能模型，为该类型气藏稳态产能预测提供了一种新方法。

(2)通过实例计算，产能模型预测结果与产能实测计算的无阻流量相对误差在±5.0%以内，模型可靠性高。

(3)裂缝渗透率、开度及条数与气井无阻流量表现为正相关，裂缝渗透率、开度及条数越大，气井无阻流量越大；窜流系数与气井无阻流量表现为“厂”字形关系，当窜流系数大于5×10-9时，气井无阻流量基本无变化。