基于应力敏感与基质收缩效应的低渗油藏数值模拟方法及应用

万晓龙，王思仪，郭西峰，兰正凯

(1.中国石油长庆油田分公司，陕西 西安 710018；2.低渗透油气田勘探开发国家工程重点实验室，陕西 西安 710018；3.中国地质大学(武汉)，湖北 武汉 430000；4.南京特雷西能源科技有限公司，江苏 南京 210000)

0 引 言

安塞油田位于鄂尔多斯盆地中部，主力产层为长6油层组，深度约为1 100～1 400 m，孔喉细小、分选性差、非均质性强，属于典型的低渗透油藏[1-2]。国内外学者普遍认为低渗透油藏储层非均质性严重，孔隙容易收缩、应力敏感性强，岩性变化非常明显[3-6]，低渗透油藏开采过程中往往只考虑应力敏感效应，忽略了基质收缩效应也会影响低渗透油藏渗流特征，降低储层的渗流能力，对油井产能影响较大[7-8]。现有的大多数商业化数值模拟软件忽略了模拟过程中基质收缩和应力敏感效应共同对计算结果的影响，不能真实地反映低渗透油藏生产特征[9]。为解决上述问题，需要建立一套考虑应力敏感与基质收缩双重效应的数学模型来描述低渗透油藏储层渗透率的变化过程，在此基础上，定量表征应力敏感与基质收缩双重效应对产能带来的影响。考虑到研究区孔隙结构的复杂性，文中基于分形理论描述渗透率，其间涉及的孔隙度变化则引入考虑应力敏感和基质收缩双重效应的关系式，由此建立考虑双重效应的渗透率演化模型，将模型计算结果与现场生产动态进行对比，验证其可靠性。

1 基质渗透率动态变化模型

低渗透油藏油井投产后，地层孔隙压力随着地层流体的采出而逐渐降低。此时地层的岩石骨架受到上覆压力的影响，岩石被压缩在孔隙壁表面，岩石骨架之间会发生一定的塑性变形。从力学角度看，颗粒间结构比较稳定、抗挤压能力强，变形能力低。但孔隙之间的塑性颗粒容易变形，尤其是泥质含量较高的岩石。当有效压力降低时，塑性变形严重，储层的渗透性主要受孔隙大小和孔隙压力的影响。当孔隙压力降低、孔隙尺寸减小，储层的渗透性急剧降低，这被称为储层的应力敏感和基质收缩效应[10]。

油井生产过程中，基质孔隙中的流体逐渐被采出，基质孔隙压力逐渐降低，但上覆岩层的压力不变。在此过程中，初始压力平衡状态被打破，形成压力差，此压力差即为孔隙上的有效载荷，有效载荷会压缩孔隙。基质的孔隙度在有效载荷的作用下变化如下：

dφm=cmidpm

(1)

式中：φm为基质孔隙度，%；cmi为基质压缩系数，MPa-1；pm为基质压力，MPa。

应力敏感导致孔隙度减小，随着流体采出，压力平衡被打破之后，支撑颗粒发生形变，基质收缩，造成孔隙度增大，因此，需要综合考虑应力敏感和基质收缩双重效应对孔隙的影响。在式(1)的基础上，应用渗流方程积分得到考虑应力敏感和基质收缩共同作用产生的孔隙度比率变化[11]：

(2)

式中：ρs为基质密度，g/cm3；R为流动常数，8.314 Pa·m3/K·mol；T为绝对温度，K；E为杨氏模量，MPa；φmi为原始基质孔隙度，%；pi为原始地层压力，MPa。

低渗油藏基质孔隙结构复杂，流体在其间的运移受到含水饱和度、孔喉连通性、迂曲度等参数的综合影响，苏海波等提出了基于分形理论的低渗透油藏油水相对渗透率模型[12]，充分考虑了孔隙结构的复杂性，文中为简化计算流程，且重在探讨基质收缩与应力敏感对渗透率的影响，因此，不考虑边界层效应，将模型简化为：

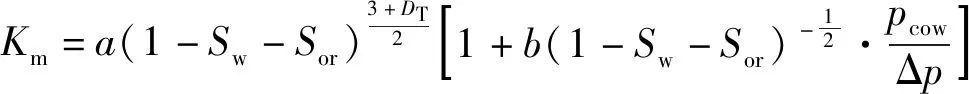
(3)

(4)

(5)

式中：Km为油相渗透率，mD；Sw为含水饱和度，%；Sor为残余油饱和度，%；DT为孔喉迂曲度的分形维数，值越大表明孔道越弯曲；pcow为油水间的毛细管力，10-6MPa；Δp为生产压差，MPa；Df，o为无量纲油相分形维数；Df为无量纲孔隙分形维数；rmin为最小有效渗流半径，m；rmax为最大有效渗流半径，m。

考虑基质收缩与应力敏感时，孔隙度比率如式(2)所示发生变化，同时也会影响分形维数的变化，进而改变渗流特征。孔隙度比率与分形维数的关系可以用式(6)～(8)来表征：

(6)

(7)

(8)

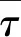
基于式(1)～(8)，可求得在考虑基质收缩与应力敏感双重效应时的低渗油藏基质渗透率演化规律。

2 数学模型的建立与求解

2.1 模型基本假设

流体渗流时忽略对流和扩散引起的质量变化，另外对于常规的黑油和组分模型，不涉及温度的变化，因此作以下假设：①地层流体充满整个多孔介质；②储层中只有易压缩、黏度恒定的运移流体；③油藏温度始终保持不变。

2.2 数学模型

(1)运动方程：

(9)

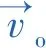
(2)连续性方程：

(10)

式中：qo为单位时间采出的油量，m3/s；So为含油饱和度，%；t为采油时间，s。

联立式(3)、(9)、(10)，得到考虑基质收缩与应力敏感效应的控制方程。

文中采用有限差分法对模型进行求解，上述模型更准确地描述了基质孔隙的变化，但未对实际储层中裂缝系统进行考虑。因此，在模拟计算时，针对孔隙-裂缝双重介质，基质孔隙采用文中模型计算，裂缝部分采用传统方法，并基于隐式裂缝压力-显式基质压力法，在渗流方程中引入对角矩阵方程，用预处理共轭梯度法求解，最终确定任意时刻的储层压力。

3 考虑双重效应的模型应用

3.1 考虑双重效应对渗透率的影响

图1为考虑与不考虑双重效应影响的渗透率变化。由图1可知，随着有效压力的下降，储层的渗透率出现不同程度的降低。有效压力为0～5 MPa，渗透率显著降低，当有效压力增加至5 MPa以后，渗透率下降幅度较小。对于低渗油藏，考虑收缩效应、应力敏感效应双重效应带来的不利影响增加。分析认为：当围压保持不变时，随着储层有效压力降低，储层有效压力升高，储层被压实而收缩，流通通道变窄、变小、甚至变少，从而使储层的渗透率下降。有效压力刚开始下降时储层的形变程度相对较大，储层的渗透率下降较快，压力敏感性较强；当有效压力增加至一定水平后，岩石的形变逐渐趋于极限，此时储层渗透率下降变慢，压力敏感性减弱。

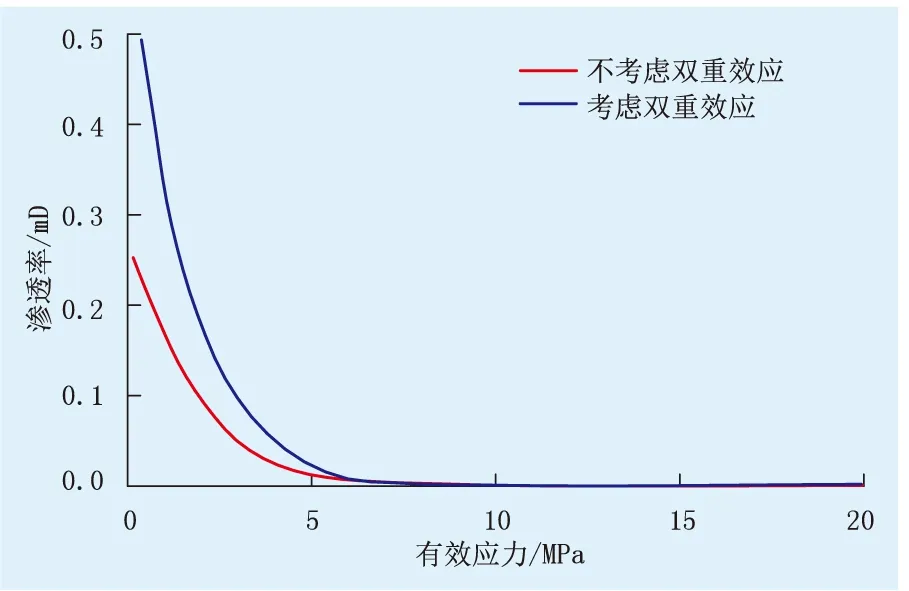
图1 考虑与不考虑双重效应影响渗透率变化Fig.1 The changes in permeability with and without dual effects

3.2 现场实例分析

基于安塞油田长6低渗透油藏已钻8口井的测井数据，利用petrel软件进行地质建模，采用序贯高斯模拟，以相模型为约束，建立孔隙度模型，如图2所示。通过协克里金函数，以相模型和孔隙度模型为双重约束，建立了渗透率模型，如图3所示。

图2 研究区孔隙度三维分布地质模型Fig.2 The geological model of 3D porosity distribution in the study area

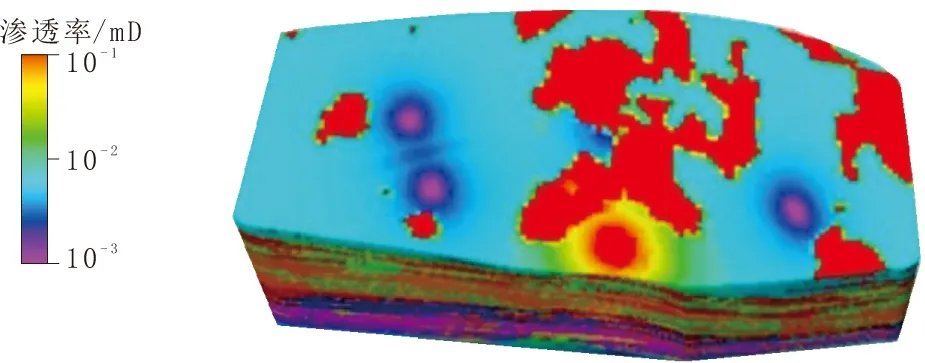
图3 研究区渗透率三维分布地质模型Fig.3 The geological model of 3D permeability distribution in the study area

综合分析安塞油田长6低渗油藏特征及岩心数据，确定低渗油藏模型参数(表1)，并赋予上述地质模型。用显式裂缝压力-隐式基质压力离散方法对数值模型求解并用实际生产数据验证。对该低渗油藏开展精细模拟，根据储层物性、油层分布特征，划分网格系统为：I方向为119个节点，J方向为65个节点，K方向为50个模拟层，网格总数为386 750个。

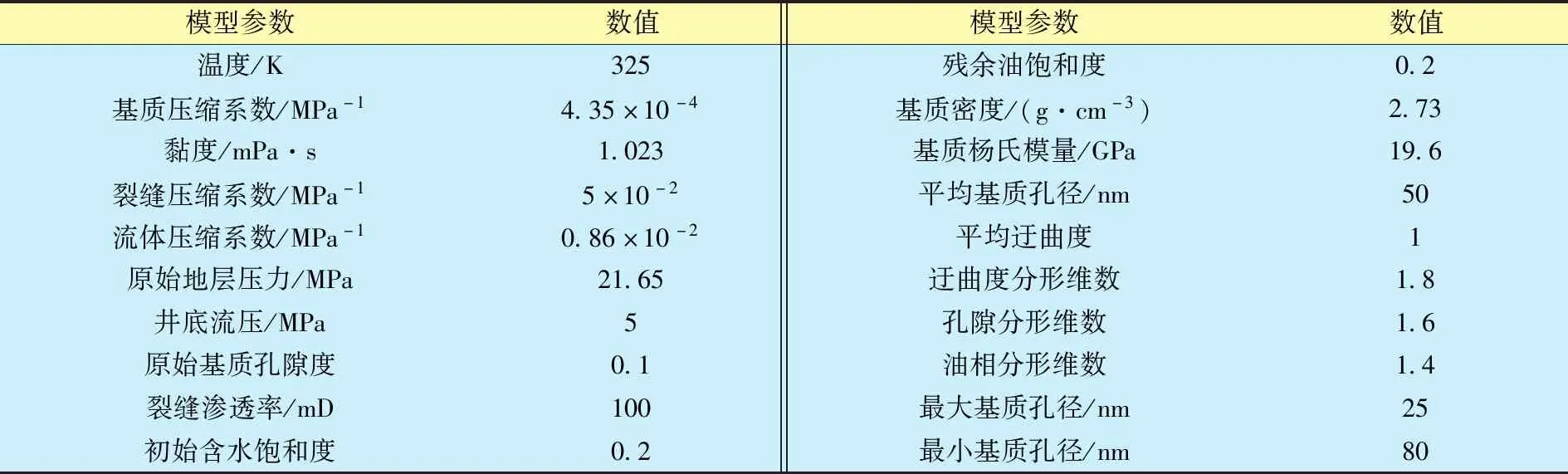
表1 长庆安塞低渗透油藏基本参数Table 1 The basic parameters of Changqing Ansai low-permeability reservoir

以研究区A9井为研究对象，进一步利用模型预测生产数据。该井2017年10月28日投产时地层压力为21.65 MPa，初期日产油为37.2 t/d。由于受到应力敏感与基质压缩双重效应，孔隙度及渗透率将发生动态变化，首先提取变化后模型中孔隙压力随生产时间变化趋势，并与Eclipse模拟结果进行对比。对比发现文中模型和Eclipse模拟孔隙压力结果基本一致(图4)，说明模型具备可靠性。

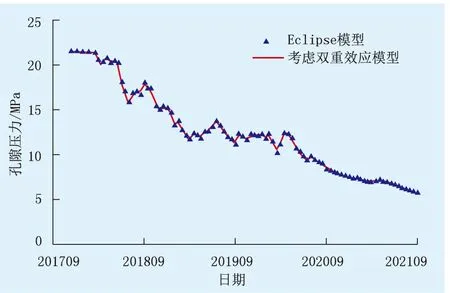
图4 研究区单井模拟数据对比Fig.4 The comparison of single well simulation data in the study area

进一步利用模型预测生产数据，生产数据如图5所示。由日产油曲线可知，该井生产早期产油情况较好，地层能量充足，产量递减速度较慢，目前日产油为16.0 t/d。考虑致密油藏储层双重效应，利用图2、3中三维地质模型开展数值模拟研究，图中计算出的该井产油量样本点数据的相关系数为0.92，而仅考虑基质应力敏感效应得到的结果相关系数为0.84，二者相比，预测准确率提高了8%，说明文中数学模型计算值与实际动态生产数据匹配程度较高，可用于预测后期油井产量。

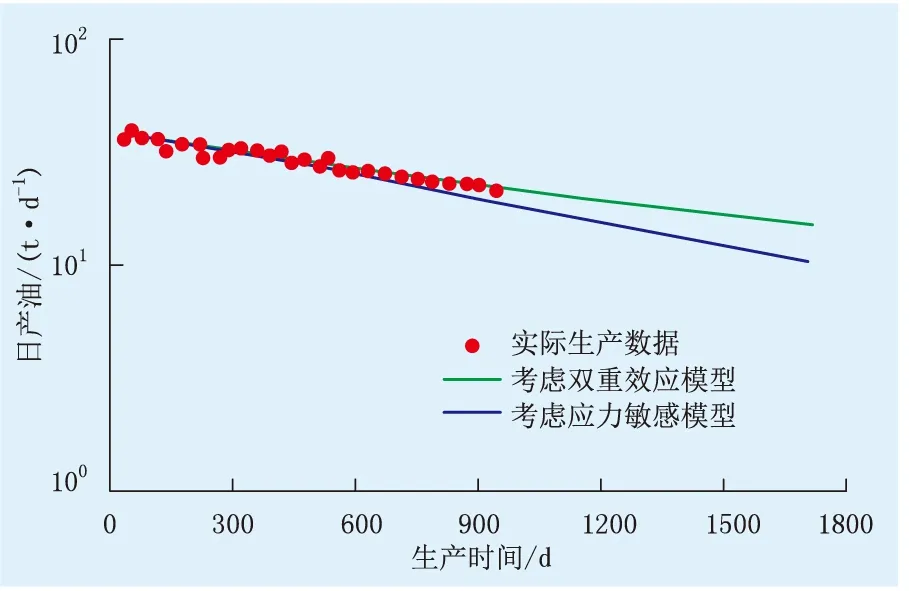
图5 考虑双重效应模型与实际日产量对比Fig.5 The comparison between the model considering the double effect and the actual daily production

4 结 论

(1)考虑应力敏感与基质收缩的双重影响，并结合分形理论对渗透率进行表征，构建了低渗油藏渗流数学模型，明确了低渗透油藏应该考虑双重效应对储层渗透率的交互影响。

(2)应力敏感效应会降低孔隙度，基质收缩效应会释放孔隙空间，模拟发现，若只考虑应力敏感效应，在低于5 MPa有效应力下，会导致储层渗透率估算偏低，但当有效应力高于5 MPa时，二者差别不大。

(3)以安塞油田长6低渗油藏A9井为研究对象，文中模型计算数据与实际日产量吻合程度较高，说明该计算模型对于预测研究区内油井生产动态具有重要意义。