基于字典学习算法的地震资料去噪处理应用研究

杨海涛, 李 琼,1b, 钱浩东, 宋 鑫, 雍 鹏

(1.成都理工大学 a.地球物理学院;b.地球勘探与信息技术教育部重点实验室，成都 610059;2.中国石油集团 川庆钻探工程有限公司钻采工程技术研究院，广汉 618300)

0 引言

信噪比、分辨率、保真度是地震数据质量的三大评价标准，其中高信噪比是三者(高信噪比、高分辨率、高保真度)的基础[1]。由于野外采集数据的时候总会受到周围环境的影响以及多次波的存在，使去噪成为解释作业之前的重中之重。相较于已有的去噪方法诸如：离散余弦变换[2]、F-K 域滤波[3]、小波变换[4]、Radon变换[5]等，压缩感知理论[6-7]的出现，打破了之前采样间隔的限制，在稀疏及重建提供了新方向。诸多学者提出了一系列稀疏重建算法和字典学习方法(ISTA算法、MP算法、BP算法以及DCT字典等)，后续又有不少学者进行优化得到了OMP算法、FISTA算法以及K-svd字典。

基于压缩感知的去噪，就是将实际数据在稀疏域中采用对应的稀疏基变成系数矩阵，再通过系数矩阵来重建地震道，再对系数矩阵进行处理，最终达到预期去噪效果。笔者应用OMP算法解决K-SVD字典的迭代问题，并与DCT字典对比研究。

1 方法原理

1.1 压缩感知理论(Compression sensing，CS)

压缩感知改变了以往抽样定理采样的前提——信号x(t)是有限带宽的，其频谱的最高频为fc，压缩感知采样的前提是 “信号x(t)可以在某变换域稀疏表示，其稀疏度为K”。与之前相比，CS是边采样边压缩，将模拟信息转化为AIC，大大降低了地震数据的采集数据量。压缩感知可分为三步：稀疏、观测以及重建(图1(b))。

图1 信号采样压缩流程Fig.1 Signal sampling compression process(a)传统信号压缩过程;(b)压缩感知理论框架

压缩感知的数学模型可以表示成式(1)。

y=Cf

(1)

其中：y为长度为m的采样结果即观测信号；C∈Rm×n(m≪n)为m×n维的采样矩阵；f为长度为n的待采样信号。由此可知，压缩感知需要的采样数据量与之前相比大大降低了，但所采集的地震数据一般都是时间域内的非稀疏信号，因此信号是需要稀疏表示来满足CS采样的前提——信号在某变换域内是K稀疏的。常用来做稀疏基的有小波、曲波(Cuverlet)、Seislet、Radon、离散余弦等。根据信号的稀疏化表示，绝大多数地震信号都能在某一个变换域内对其稀疏化表示，因此可表示为[8]式(2)。

f=Ψx

(2)

其中：Ψ∈Rn×n是稀疏矩阵；f是被信号x的稀疏表示。

将式(1)代入式(2)式可得式(3)。

y=Cf=CΨx

(3)

可以将CΨ合并成一个矩阵B∈Rm×n，可得：

y=Bx

(4)

由于矩阵B是一个m×n维矩阵，且m≪n，因此方程组是一个欠定方程组。Candes等[6]提出有限等距性质(Restricted Isometry Principle, RIP)即：零空间特性、约束等距性和相干程度低。由上述的理论可知(常数矩阵)δk∈(0,1)应需满足：

(5)

观测矩阵一般使用Gauss矩阵，因为随机高斯矩阵与大部分固定稀疏基矩阵是不相干的。对地震数据进行观测，故选用正交基作为变换基时，B是满足RIP性质的[9]。

当满足RIP条件时，信号重构最直接的方法是L0范数的最优化问题：

(6)

由于式(6)的求解是个NP(欠定)问题。Candès[6]指出，可以把复杂性和不稳定性较高的L0范数最优化问题，转化为等价的L1范数最优化问题，因此式(6)可转化为：

argmin‖x‖1s.ty=Bx

(7)

而关于信号重构，目前可大致分为两大类：

1)凸规划算法。在稀疏重建模型中，Candès[5]指出可以把复杂性和不稳定性较高的L0范数最优化问题，转化为等价的L1范数最优化问题。诸多学者相继提出基追踪(BP)、梯度下降法、凸集交替投影法(POCS)以及迭代阈值法等方法。

2)贪婪迭代算法。这类方法通过从感知矩阵列中选出一个和观测矩阵最匹配的原子，经过不停地迭代重构出稀疏信号，主要包括匹配跟踪算法以及其优化算法——正交匹配追踪算法等。故OMP算法被经常使用，是基于MP算法的基础做斯密特正交化，使迭代速率明显加快了。

1.2 信号质量客观评价方法

信号质量客观评价方法大致以下几种：①信噪比(Signal to Noise Ratio, SNR);②均方误差(Mean Square Error, MSE);③峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)[10]。

信噪比：

(8)

其中：x、y分别为去噪信号和原始信号，且均为M*N阶矩阵。

峰值信噪比：

(9)

其中，MSE为均方差误差。

1.3 正交匹配追踪算法

正交匹配跟踪算法(Orthogonal Matching Pursuit，OMP)的原理是基于MP算法原理，是利用筛选与误差相关性最大的原子，利用原子的线性组合去重构出最优近似信号[11]，OMP算法具体流程如图2所示。

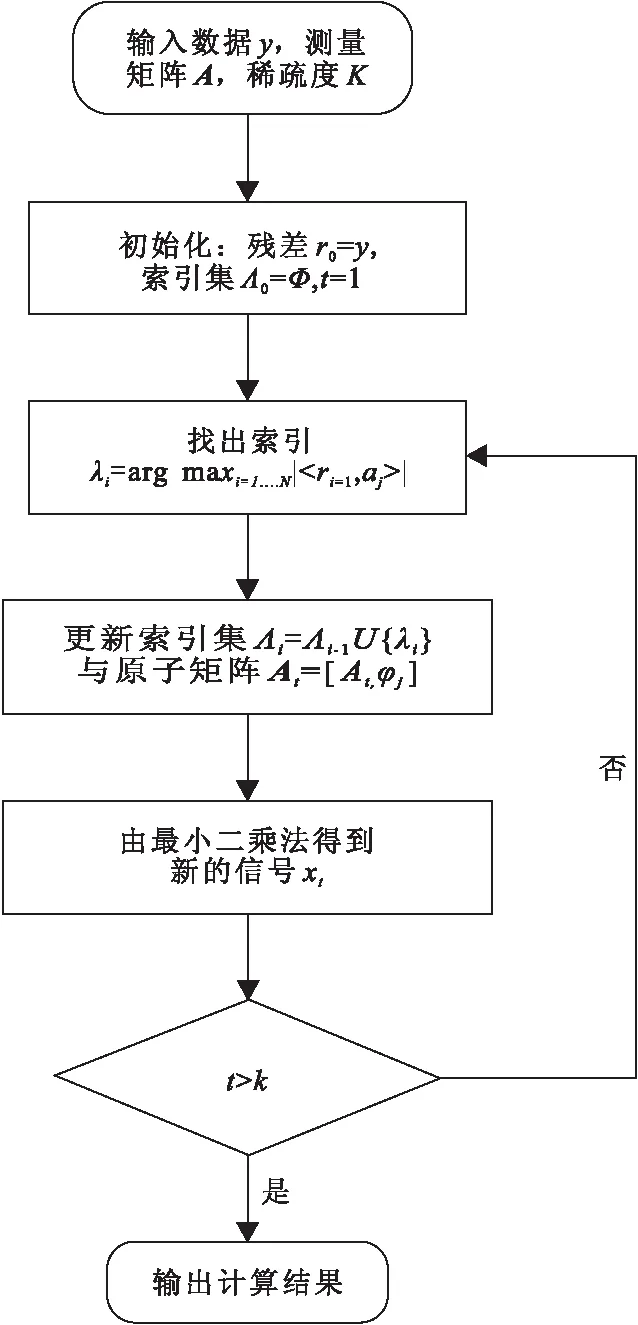
图2 OMP算法流程图Fig.2 Algorithm flowchart of OMP

1.4 DCT字典

DCT 字典是通过离散余弦变换的正交变换来得到的，能较好地对周期信号进行分辨，其特点为能量集中，低频部分为其主要集中部分，同时可以去掉高频信号中的无用的一部分，因此适用于对地震资料局部的特征进行处理反变换为式(11)。

给定一组序列y(n)，经过DCT变换得到式(10)。

(10)

(11)

式中0≤n≤N-1，其矩阵形式为：

Yc=CNy

(12)

其中CN经过DCT变换就可以得到字典D(图3)。

图3 DCT字典Fig.3 DCT dictionary

1.5 K-SVD字典学习

K-SVD是一种字典学习的构建算法，从矩阵角度分析，其目标就职是把输入的训练样本F矩阵分解成两部分：(字典)D和(稀疏矩阵)S。K-SVD字典学习其实是K-means算法的一种改进算法，利用稀疏约束条件来进行制约，然后利用逼近信号与原始信号差值的奇异值分解来不断迭代更新，求解有两个阶段，即稀疏编码和字典学习[12]。与固定字典DCT相比，K-SVD字典多了更新训练的过程，在对地震资料进行去噪处理时，是通过对实际信号所得出的自适应字典，比固定字典更具稳定性。首先假设Y为M*N阶训练样本矩阵，K-SVD算法中求解系数矩阵时采用OMP算法。在更新字典阶段：

(13)

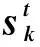
图4 K-SVD学习字典Fig.4 K-SVD learning dictionary

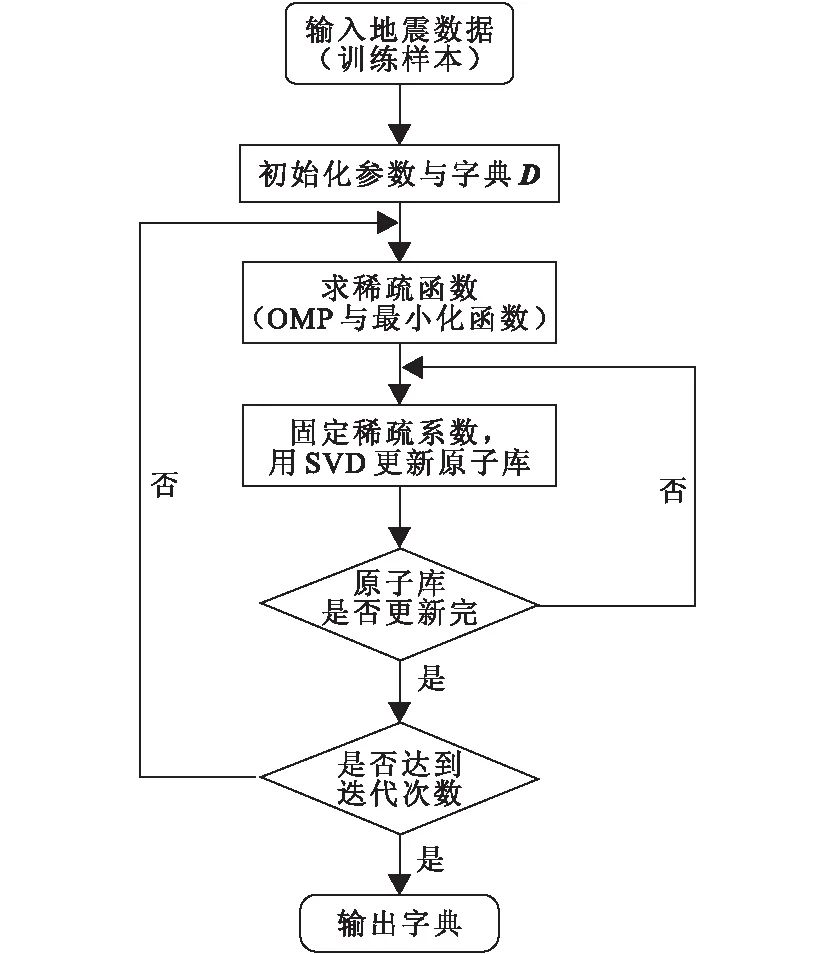
图5 K-SVD学习字典流程Fig.5 Algorithm flowchart of K-SVD

3 模型测试

为了证明K-SVD与DCT变换矩阵下的OMP算法的去噪效果，笔者选用主频30 Hz的雷克子波，设计了如图6(a)的三层模型的弹炮合成记录与图6(b)所示的六层地层模型，图6(a)设计为总长为2 560 m，道间距为5 m，波速分别为2 000 m/s、2 400 m/s、2 300 m/s，因此该模型513道接收。图6(b)设计为总长为5 120 m，道间距为10 m，波速分别为2 300 m/s、3 200 m/s、5 500 m/s、3 700 m/s、6 000 m/s，因此该模型也为513道接收。

图6 原始模型及加噪单炮合成记录Fig.6 The original model and noisy single shot synthesis record(a)三层单炮记录；(b)六层单炮记录；(c)三层加噪单炮记录；(d)六层加噪单炮记录

图6(c)和6(d)是为加噪模型的单道地震合成记录，对比原始模型可以明显看到噪音的存在。以两种字典学习型进行去噪，从而得到如图7所示的去噪效果图。对于不同地层，就峰值信噪比来说，表1的PSNR值是由Matlab计算出来的，从表1中可以看出，两种学习字典的峰值信噪比PSNR都随着地层的增加而减小；为了更清晰对比，由图7(e)与7(f)、7(g)与7(h)可知，对同一地层来说，从图7中红线框中可以看DCT字典对同相轴的损害要更高一点，可以看到K-SVD字典明显比DCT字典的效果好，但K-SVD较之DCT，由于在字典的稀疏编码阶段通过奇异值分解不断地更新字典，在噪声强度较大的情况下，去噪效果有了显著的提高，且具有更强的稳定性；缺点是由于迭代的次数比较多，导致运行速度较慢。K-SVD算法中求解系数矩阵时采用OMP算法，是在MP的基础上进行施密特正交化，这样就不用再多次选择原子，故减少了运算时间。

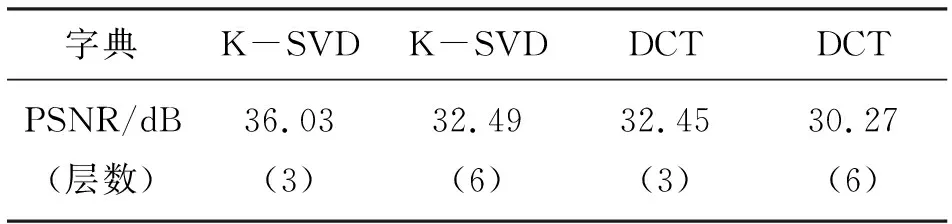
表1 降噪方法的评价指标表Tab.1 Noise reduction evaluation index table

图7 去噪图及残差图Fig.7 Result and residual graph(a)三层模型DCT效果图；(b)三层模型K-SVD效果图；(c)六层模型DCT效果图；(d)六层模型K-SVD效果图；(e)三层模型DCT残余图；(f)三层模型K-SVD残余图；(g)六层模型DCT残余图；(h)六层模型K-SVD残余图

4 实际资料处理效果评价

实际地震资料为某工区叠后资料，根据已有的地质、测井等资料的查证，可以知道该工区地层的目的层频带范围大体位于8 Hz至70 Hz之间，主频分布在20 Hz至28 Hz之间。由于研究区的侏罗系三工河组储层砂体构造整体复杂，砂层横向变化大，且整体较薄，同时受煤层强反射的影响，造成了砂体识别困难。

图8(b)为加上随机噪声后的剖面图，分别应用DCT与K-SVD字典进行去噪处理，得到图9 (a) 与图9 (b)，为了更清晰地看到去噪效果，特输出如图9(c)与图9(d)的残差图。

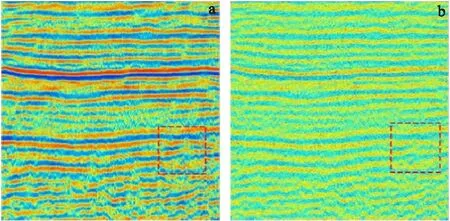
图8 原始剖面与含噪叠后地震剖面Fig.8 The original profile noisy post-stack seismic section(a)原始剖面；(b)加噪剖面

图9 去噪图及残差图Fig.9 Result and residual graph(a)DCT字典去噪图；(b)K-SVD去噪效果图；(c)DCT残余图；(d)K-SVD残余图

图9(a)、图9(b)与图8(b)对比分析，再综合表2的PNSR(峰值信噪比)可知，K-SVD和DCT去噪效果能力都较好，都能很好地去除大量的随机噪声。残差图中只显示噪声点，从图9(c)、图9(d)中对比可看到，K-SVD去噪精度更高一些，而且DCT字典对有用信息有所损害(图中红色虚线框)，学习字典则对地震资料的纹理细节无损害，没有对原始信号品质产生破坏。

表2 降噪方法的评价指标表Tab.2 Noise reduction evaluation index table

从重构信息部分来看，就地震能量破坏程度来说，K-SVD较DCT轻，同时图9(b)包含的信息量更为丰富，红色线框处同相轴对比更明显，有效信息破坏程度较之9(a) 更轻，几乎没有破坏原始信息，信噪比高很多。

5 结论

笔者通过两种学习字典的去噪与重建效果对比研究：

1)表明两种字典都可以有效地对地震资料进行去噪，对比分析可知，K-SVD结合了压缩感知下的匹配追踪算法的去噪效果要优于DCT字典，DCT字典对地震资料的纹理细节有所损害，而K-SVD学习字典则几乎没有损害。

2)随着地层复杂性的提高，K-SVD学习字典能够根据实际资料训练出自适应的学习字典，更具稳定性，去噪效果之后剖面也更加清晰，能得到更多有用的分层信息。

3)字典学习可以提高构造解释与储层预测的准确性，对于海量地震数据的解释分析工作具有极其重要的意义。