如何正确运用方差分析——拉丁方设计定量资料一元方差分析

胡纯严 ，胡良平 ，2*

（1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029

拉丁方设计是考察一个试验因素和两个非试验因素对定量观测结果影响的一个试验设计方法。本文将介绍该设计类型的要点、定量资料一元方差分析的计算公式，以及基于SAS软件实现拉丁方设计定量资料一元方差分析的方法。

1 拉丁方设计的要点

1.1 概述

当试验中涉及一个试验因素，还涉及两个区组因素（通常包括个体因素和时期因素），若它们之间的交互作用不存在或可以忽略不计，一种节省样本含量的设计方法为拉丁方设计。根据试验因素的个数和水平数，可将拉丁方设计分为一般拉丁方设计（简称拉丁方设计）［1-2］和希腊拉丁方设计［3］或正交拉丁方设计［4］；还可以按“单个体型区组因素”与“多个体型区组因素”和有无重复试验，进一步划分拉丁方设计类型。这些细分的拉丁方设计的区别主要体现在“实用性（例如，单个体型区组因素且无重复试验，可以最大限度减少样本含量，反之亦然）”与“分析结果的精确度（例如，当不同时期测量结果存在携带效应时［5］，基于常规方差分析模型计算得到的结果不够精确）”两方面。

1.2 单个体型无重复试验5×5拉丁方设计

【例1】为了比较五种防护服对脉搏数的影响，拟选择五名受试者在五个不同日期进行试验，试验设计和定量观测结果见表1［6］。试分析五种防护服对脉搏数影响之间的差别是否有统计学意义。

表1 穿五种防护服测得的脉搏数（次/分）

防护服种类是一个试验因素，它有5个水平，即A、B、C、D、E；试验日期和受试者是两个区组因素；试验因素的5个水平随机排列成5×5的拉丁方阵（注：最初人们采用拉丁字母而不是英文字母）的形式，假定三个因素之间的交互作用可以忽略不计。这样的试验安排被称为拉丁方设计。

1.3 单个体型有重复试验3×3拉丁方设计

【例2】为了研究三种饲料对奶牛产奶量的影响，拟选择6只奶牛进行试验，每只奶牛在三个时期被随机喂养三种饲料。试验设计和定量观测结果见表2［5］。试分析三种饲料喂养的奶牛产奶量之间的差别是否有统计学意义。

饲料种类是一个试验因素，它有A、B、C3个水平；观测时期和奶牛编号是两个区组因素；试验因素的3个水平随机排列成3×3的拉丁方阵形式（见表2前3行），假定三个因素之间的交互作用可以忽略不计，这样的试验安排被称为拉丁方设计。为了提高试验结果的精确度，再选择3只奶牛，采用类似的设计，但拉丁方阵需要重新排列，见表2的后3行。这就形成了单个体型且有两次重复试验的3×3拉丁方设计。

表2 三种饲料喂养的奶牛产奶量的观测结果

1.4 多个体型无重复试验7×7拉丁方设计

【例3】为比较7种药液（分别为A、B、C、D、E、F、G）的作用强度，用7个离体肠管标本进行试验。将它们中的每一个视为一个区组，再将每个区组内的肠管均分成7份，随机接受7种药液的处理，然后测定作用强度的大小。试验设计和结果见表3［7］。试分析7种药液的平均作用强度之间的差别是否有统计学意义。

表3 7种药液作用强度的测定结果

2 拉丁方设计定量资料一元方差分析的计算公式

拉丁方设计定量资料一元方差分析的计算公式见表 3［3，5］。

表3 r×r拉丁方设计定量资料一元方差分析表

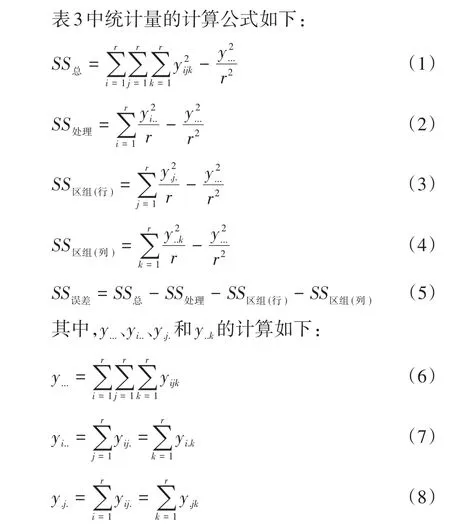
3 拉丁方设计一元定量资料的实例与SAS实现

3.1 对例1的分析与解答

【分析与解答】设例1资料所需要的SAS程序如下：

【SAS输出结果及解释】

以上第一部分输出结果表明：方差分析的模型有统计学意义（F=6.80，P=0.001 1）。

以上第二部分输出结果表明：仅受试者脉搏数的均值之间的差别有统计学意义，这意味着个体之间的差别比较大；而不同防护服对受试者脉搏数影响之间的差别不明显。

以上输出的是各种防护服所对应的脉搏数的均值和标准差。C、E、A三种防护服对应的均值稍高一点。

因为研究者关心的是防护服对脉搏数的影响情况，故不必要将两个无统计学意义的因素（因为其中包含了试验因素：防护服种类）删除掉，采用单因素5水平设计定量资料一元方差分析来处理受试者因素。

3.2 对例2的分析与解答

【分析与解答】设例2资料所需要的SAS程序如下：

【SAS输出结果及解释】

以上第一部分输出结果表明：方差分析的模型有统计学意义（F=21.07，P=0.000 1）。

以上第二部分输出结果表明：饲料种类（diet）、奶牛个体（cow）和观测时期（time）三个因素对结果的影响均有统计学意义。

以上输出的是三种饲料所对应的奶牛产奶量的均值和标准差，结果显示：饲料C所对应的均值（72.67）最大，饲料B所对应的均值（57.50）次之，饲料A所对应的均值（45.17）最小。它们之间两两比较的结果见图1。

图1 基于TUKEY法对饲料种类三个水平下均值进行两两比较

由图1可看出：饲料C与饲料B的均值差别无统计学意义，饲料B与饲料A的均值差别无统计学意义；但饲料C与饲料A的均值差别有统计学意义。由于TUKEY法控制的是最大试验误差率［1，7］，所以，两两比较的结果显得差别不够明显。若采用LSD法进行两两比较，所得结果见图2。

图2 基于LSD法对饲料种类三个水平下均值进行两两比较

由图2可看出：饲料C与饲料B、饲料A的均值之间差别都有统计学意义。因为LSD法控制的是比较误差率（要求放宽松了）［1，8］。

3.3 对例3的分析与解答

【分析与解答】设例3资料所需要的SAS程序如下：

【SAS输出结果及解释】

以上第一部分输出结果表明：7种药液对应的作用强度均值之间的差别有统计学意义（F=14.21，P＜0.000 1），而标本的均值之间、测定次序的均值之间的差别均无统计学意义。

将7×7拉丁方设计视为单因素（特指“药液种类”）7水平设计，重新对资料进行方差分析（见前文SAS程序的第2个过程步）。以上第二部分输出结果表明：7种药液的作用强度的均值之间差别有统计学意义（F=12.60，P＜0.000 1），不同药液的作用强度是不尽相同的，具体两两比较的结果见图3。

由图3可看出：药液B的作用强度最强，其均值为17.43，此均值与其他6个均值之间的差别均有统计学意义；药液A的作用强度明显低于药液B，其均值为7.86，此均值与药液C的均值之间差别有统计学意义，而与其他均值差别均无统计学意义。

图3 基于TUKEY法对药液种类7个水平下均值进行两两比较

4 讨论与小结

4.1 讨论

在本文例3中，若每行上的试验是在同一离体肠管标本上进行7次重复试验，就属于单个体型区组因素的7×7拉丁方设计，这样从第2个时间点到第7个时间点上观测的结果都会受到之前各时间点上所接受处理的影响，结果的准确性就会降低。

在本文例2中，若第2个拉丁方设计不是“重复试验”，而是第2个试验因素3个水平（设为α、β、γ）的随机排列出来的3×3方阵，被称为“希腊拉丁方设计”［3］，其含义是两个试验因素的水平分别用“拉丁字母”和“希腊字母”来表示。并且，用这两种字母排列成的两个3×3方阵彼此之间是互相正交的。因此，这种拉丁方设计又被称为正交拉丁方设计［4］。

值得注意的是：在拉丁方设计（涉及1个试验因素2个区组因素）和希腊拉丁方设计（涉及2个试验因素2个区组因素）中，要求因素之间互相独立。若实际问题中的因素不满足独立性要求，在设计表格的行列交叉处应尽可能进行2次及以上独立重复试验。否则，结果的可信度很低。

4.2 小结

本文介绍了拉丁方设计的要点，以及拉丁方设计定量资料一元方差分析的计算公式；借助SAS软件对两个实例的拉丁方设计定量资料进行一元方差分析。在讨论中，提到了应用拉丁方设计需要了解的几个问题。