如何正确运用方差分析——交叉设计定量资料一元方差分析

胡纯严 ，胡良平 ，2*

（1.军事科学院研究生院，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029

交叉设计是考察一个试验因素和两个区组因素（即重要非试验因素）对定量观测结果影响的一个试验设计方法。本文将介绍该设计类型的要点、定量资料一元方差分析的计算公式，并基于SAS软件实现交叉设计定量资料一元方差分析。

1 交叉设计的要点

1.1 概述

当试验中涉及一个试验因素，还涉及两个区组因素（其中一个为时期因素，另一个为个体因素）时，若它们之间的交互作用不存在或可以忽略不计，一种节省样本含量的设计方法为交叉设计。根据试验因素的水平数和时期因素的水平数，可将交叉设计分为三种类型，即2×2交叉设计（或二阶段交叉设计）、3×3交叉设计和三阶段交叉设计［1］。

若每个区组中只有一个受试对象（观察单位），则称为“单个体型交叉设计”；否则，就称为“多个体型（不能节省样本含量）交叉设计”［2］。

1.2 2×2交叉设计

【例1】在针麻研究中，为比较A、B两种参数电针刺激后痛阈值上升情况，以条件近似的16只大白鼠进行交叉试验。先将每两只条件相同的大白鼠配成一对，共8对。用随机方法决定每对中一只大白鼠接受刺激的顺序，另一只大白鼠接受刺激的顺序相反。试验结果如表1所示［3］。

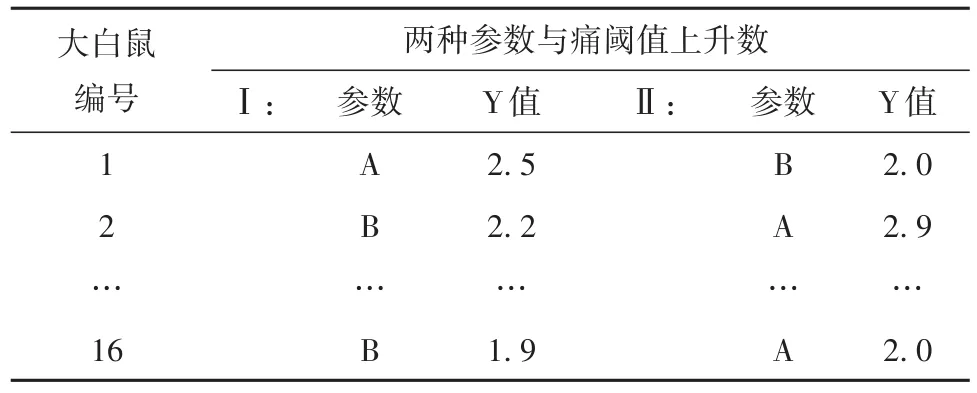
表1 给大白鼠两种不同参数电针刺激后痛阈值上升数（mA）

1.3 3×3交叉设计

【例2】假定为了研究A、B、C三种药物对高血压的治疗效果，希望考察三种药先后用于同一位患者的疗效，于是进行了如下试验研究。从高血压患者中随机选取12名，随机均分成6组，每组患者接受药物的顺序依次为 ABC、ACB、BAC、BCA、CAB、CBA，观测每次服药后的血压值。设计与资料见表 2［1］。

表2 A、B、C三种药物用于每一位高血压患者的疗效观测结果（kPa）

1.4 三阶段交叉设计

【例3】假定有A、B两种治疗高血压的药物，拟通过小规模的预试验来进行探索性研究，以判断两种药物的疗效之间的差别是否有统计学意义。研究者给出了以下两种设计方案。

方案一：从高血压患者中随机选取12名，再用随机的方法让其中6名患者在三个时期内按先A后B再A的顺序接受治疗，记为ABA；另外6名患者在三个时期内按先B后A再B的顺序接受治疗，记为BAB。观测的指标是血压下降值（kPa）。设计与资料见表 3［1］。

表3 方案一中高血压患者在三个时期服用两种药的血压下降值（kPa）

方案二：从高血压患者中随机选取12名，按病情、性别、年龄等重要的非试验因素将12名患者配成6对，每对中的两名患者在前述重要的非试验因素方面非常接近。再采用随机的方法让每对中的一名患者在三个时期内按先A后B再A的顺序接受治疗，记为ABA；另外一名患者在三个时期内按先B后A再B的顺序接受治疗，记为BAB。观测的指标是血压下降值（kPa）。设计与资料见表4［1］。

表4 方案二中高血压患者在三个时期服用两种药的血压下降值（kPa）

2 交叉设计定量资料一元方差分析的公式

2×2交叉设计定量资料一元方差分析的计算公式见表 5［3-4］。

表5 2×2交叉设计定量资料一元方差分析表

表5中各统计量的计算公式如下：

3 交叉设计一元定量资料的实例与SAS实现

3.1 对例1的分析与解答

【分析与解答】设例1资料所需要的SAS程序如下：

【SAS输出结果及解释】

以上第一部分输出的是交叉方差分析模型的计算结果，因F=29.68，P＜0.000 1，说明该模型具有统计学意义。

以上第二部分输出的是交叉设计模型中的三个因素的方差分析结果，除时间因素（time）外，另两个因素都有统计学意义。可以在上面的过程步程序中删除时间因素（time）后重新运行程序，得到如下结果：

在以上第一部分结果中，与前文类似结果相比，误差自由度由14增加为15，误差均方由0.025 669 64下降为0.024 479 17。

在以上第二部分结果中，与前文类似结果相比，两个因素对应的F值都有所增加且P值相应地有所变小。说明采用现在的随机区组设计定量资料一元方差分析模型拟合此定量资料更合适。

由上述结果可知，A参数电针刺激后痛阈值的均值（2.87）高于B参数电针刺激后痛阈值的均值（2.34）。

3.2 对例2的分析与解答

【分析与解答】设例2资料所需要的SAS程序如下：

【SAS输出结果及解释】

以上第一部分输出的是交叉方差分析模型的计算结果，因F=9.95，P＜0.000 1，说明该模型具有统计学意义。

以上第二部分输出的是交叉设计模型中的三个因素的方差分析结果，除时间因素（time）外，另两个因素都有统计学意义。可以在上面的过程步程序中删除时间因素（time）后重新运行下面的程序：

【SAS输出结果及解释】

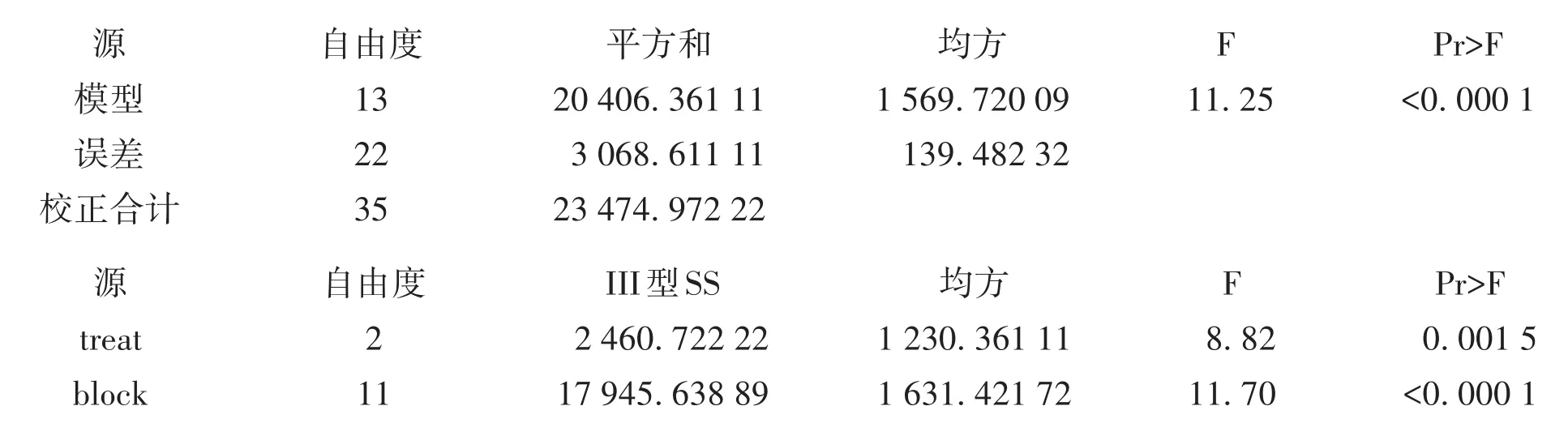
以上第一部分结果中，与前文类似结果相比，误差自由度由20增加为22，误差均方由138.761 11上升为139.482 32。

以上第二部分结果中，与前文类似结果相比，两个因素对应的F值略微减少，P值也变小。说明采用现在的随机区组设计定量资料一元方差分析模型拟合此定量资料更合适。

以上输出的结果是三种降压药对应的血压平均值及标准差。

由图1可看出：A药与B药所对应的均值之间的差别具有统计学意义，B药的疗效好于A药的疗效。

图1 采用TUKEY法对三种药物所对应的均值的两两比较结果

3.3 对例3的分析与解答

【分析与解答】设例3资料所需SAS程序如下：

【SAS输出结果及解释】

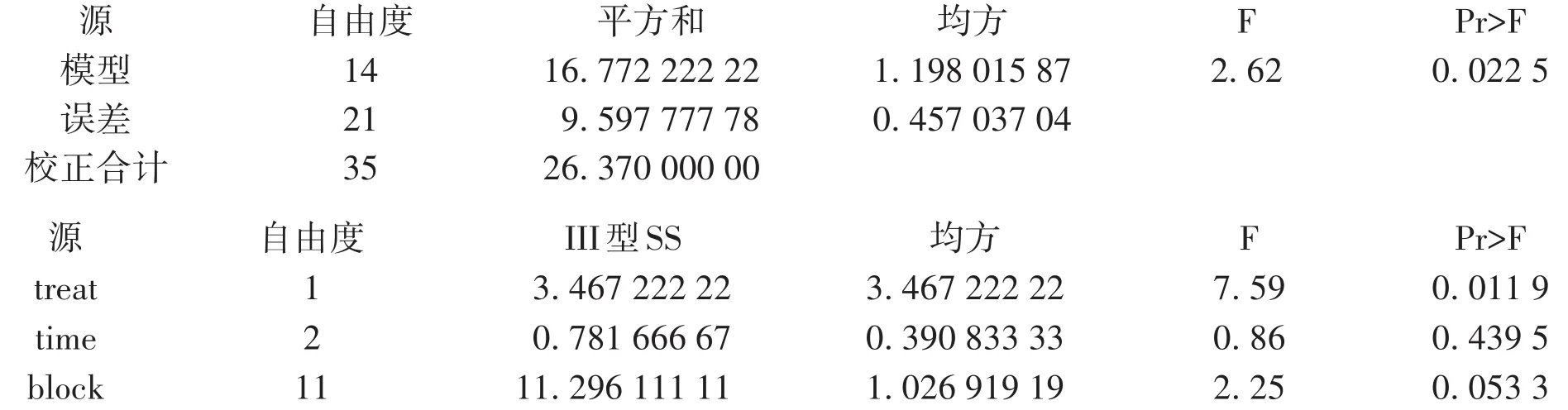
以上第一部分输出的是交叉方差分析模型的计算结果，因F=2.62，P=0.022 5，说明该模型有统计学意义。

以上第二部分输出的是交叉设计模型中的三个因素的方差分析结果，仅试验因素（treat）具有统计学意义（F=7.59，P=0.011 9）。若按单因素两水平（因为试验因素只有两个水平）设计定量资料一元方差分析计算，则输出结果如下：

以上输出结果是单因素两水平设计定量资料一元方差分析模型的计算结果，F=7.36，P=0.010 4，说明此模型有统计学意义。此结果的第一行，与前面关于模型的分析结果相同（因为模型中只有一个两水平的试验因素）。

由上述结果可知，A药的平均血压下降值（3.11）大于B药的平均血压下降值（2.39）。

4 讨论与小结

4.1 讨论

本文给出的3个实例都属于“单个体型区组因素（即每个区组内只有一个受试对象）的交叉设计”，在时期因素的两个或多个水平下对每个区组里的一个受试对象进行重复试验和测量，严格地说，各区组上的多个测定结果之间存在一定程度的相关性，故不符合方差分析关于定量资料应满足“独立性”的要求；更为严重的是，在第1个时间点之后的多次测定结果不可避免地要受到之前“处理”的影响，特别是当试验因素类似“药物种类”或“药物剂量”时，这种影响可能是持续的逐渐累积的过程，这种现象被称为“携带效应”［5］。因此，单个体型交叉设计定量资料一元方差分析结果的精确度不够高。解决这个问题的措施有如下三个：其一，采用多个体型区组因素的交叉设计，即每个区组里应包含多个受试对象（其数目应等于时期因素的水平数）；其二，可尝试采用混合效应模型处理定量资料，通过寻找适合的方差和协方差结构的混合效应模型［6-7］，最大限度地提高结果的精确度；其三，可尝试采用广义估计方程方法求解交叉设计定量资料方差分析模型中的参数［8-9］。

4.2 小结

本文介绍了交叉设计的要点，介绍了交叉设计定量资料一元方差分析的计算公式；借助SAS软件对三个实例（即三种不同类型）进行交叉设计定量资料的一元方差分析。在讨论中，指出单个体型交叉设计存在的不足之处，并提供了三个解决措施。