基于UU试验方法在黏土地基承载力计算方法研究

覃震林

(柳州市勘察测绘研究院有限公司，广西 柳州 545006)

1 引 言

《地基基础设计规范》和《高层建筑岩土工程勘察标准》计算地基承载力用到的两个理论公式，都是以摩尔-库伦破坏理论，即基于地基土受力达到抗剪强度而破坏。由于土的抗剪强度指标因地基土受力条件不同而不同，受力条件又由地基土的排水条件和加荷速率决定，对于正常固结黏土地基，采用不固结不排水UU指标计算地基承载力。但现行的《土工试验方法标准》采用的UU试验加压方法并不符合地基实际受力条件，其得出的抗剪强度指标用于地基承载力计算不尽合理：

按现有的勘察程序，在钻探现场对主要受力层土层(假设其为同一层土，土层厚 8 m)按竖向间隔 1 m～2 m取样，如此最上一个样与最下一个样深度相差了 3 m～6 m，原位所受的竖向压力相差了约 55 kPa～110 kPa。而用如此不同压力下的“同一土层”试样进行“混合”UU试验，只会得到一条倾斜的抗剪强度线而不是水平线。原因就出在不同压力下的“同一土层”试样进行“混合”UU试验。本文建议将一倍基宽深度内划分几个力学亚层，每一亚层因为厚度小而可视为“同一深度即有着同一剪前压力”，按各亚层的实际受力对试样进行加压，并将各亚层的CU按厚度加权平均得到的标准值作为承载力计算参数更合理。

2 工程案例对比分析

2.1 工程概况

分析地基中一点的应力状态变化过程，为方便起见，设一无埋式筏板基础，厚层饱和正常固结黏土，天然重度γ=20 kN/m3，无地下水。基底下亦即地面下 5 m深度的一个点，如图1所示：

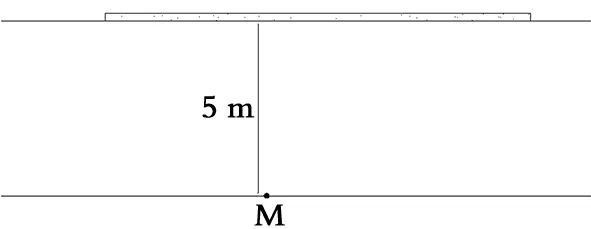
图1 基底下某深度1个土单元示意

2.2 土单元应力过程分析

对于正常固结黏土，一般认为总应力固结不排水CU强度包线、固结排水CD强度包线及有效应力强度包线都是通过原点的直线，其中效应力线是“真正的”破坏强度线，CD线可认为是有效应力强度线。

未设筏基前，此点受荷为：大、小两个主应力分别为竖直向和水平向，此时该点已完成了固结(自重固结)，竖直向σZ=σ1=rh=20×5=100 kPa，水平向应力σX=σ3=K0×σ1=0.7×100=70 kPa，为便于描述，设此时的应力状态为X1(前缀X表示“现场的”)。注意到此状态X1已有了主应力差。详细描述其受荷过程应是：

在地质历史上，该点自重压力σZ=σ1从0逐渐增加到 100 kPa，同步形成静止侧压力σX=σ3，按σX=σ3=K0×σ1的关系式，σX=σ3亦从0开始，逐渐增加到K0×100=70 kPa。这一漫长的地质过程属于固结排水剪切CD过程，如图2所示。

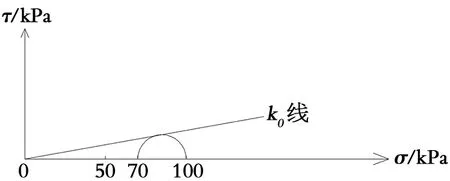
图2 K0条件下土单元的莫尔应力圆

之后，基础和上部结构形成了附加荷载P0=P，在土自重压力和建筑附加压力工作同作用下，土中此点大、小两个主应力方向较X1状态发生变化，不再是竖直—水平向，此时的应力状态为X2，注意到此状态也已有了主应力差。此点是否达到破坏按摩尔-库伦破坏准则即是地基承载力的验算问题，譬如按塑性展开深度确定的地基承载力(在现行的地基基础规范中的5.2.4式—1/4板宽展开深度)。

2.3 土单元破坏原理

据“密度—有效应力—抗剪强度”的唯一性关系规律，对于同一种饱和正常固结黏土，存在单一的有效应力强度包线(超固结黏土也存在如此关系)，剪前孔隙比小则极限应力圆越大，预固结应力越大，则极限应力圆越大。

2.4 不同试验方法土单元破坏过程对比分析

以自然环境下(现场)正常固结黏土为例，其多接近或达到饱和，在现代的建筑施工速度较快，地基在建筑荷载产生的附加荷载下来不及排水固结，故试验采用不固结不排水UU，有如下3种UU试验方法，具体为：

方法一：按《土工试验方法标准》

以3件～4件试样为一组至少6组进行试验备样，据“密度(孔隙比)—有效应力—抗剪强度”的唯一性关系规律，这几组试样须取自同一层土同一深度，以使其具有相同的剪前孔隙比。

首先，对试样进行人工饱和处理，为便于对下面加荷过程叙述的形式统一，对各试件进行0压力围压加荷，即预固结压力σc=0，此时各试件应力状态为同一个点圆A。之后，分别对各试样施加不同大小的周围压力增量△σ3=100 kPa、200 kPa、300 kPa、400 kPa，即σ3=100 kPa、200 kPa、300 kPa、400 kPa，△σ3施加过程试样处于密封不排水状态，即不固结，周压增量△σ3全部由孔隙水承担，此时各试样的应力状态仍为一个个点圆，但位置不同；最后，施加主应力差qu=σ1-σ3至剪破，得到几个极限总应力圆，如图3所示。

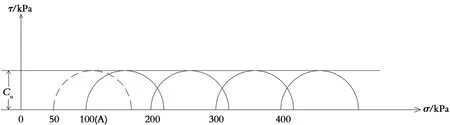
图3 σc=0的UU莫尔极限应力圆

由于饱和正常固结黏土在同一个剪前孔隙比下(同一个预固结压力σc=0 kPa)，故在UU剪切过程中不管周围压力增量△σ3(由于预固结压力σc=0 kPa，也即周压σ3=)是多大，极限总应力圆的主应力差qu大小都相同，全部σ3(由于预固结压力σc=0 kPa，也即周压σ3=△σ3)全部转为超静孔隙水压力，其对抗剪的贡献为零，故形成的几个极限应力圆大小相同，位置各异，有效强度包线仅一条，此为水平包线，qu/2=Cu。

方法二：按《地基基础设计规范》

首先对试样进行人工饱和处理，然后按《地基基础设计规范》4.2.4条对每一组试样施加自重应力值的预固结周围压力σc=σZ=100 kPa，此时各试样应力状态为同一个点圆B。固结后分别施加不同大小的周围压力增量△σ3=0 kPa、100 kPa、200 kPa、300 kPa，即σ3=100 kPa、200 kPa、300 kPa、400 kPa，△σ3施加过程试样处于密封不排水状态，即不固结，周压增量△σ3全部由孔隙水承担，此时各试样的应力状态为一个个点圆，但位置不同；最后，施加主应力差qu=σ1-σ3至剪破，得到几个极限总应力圆，如图4所示。

图4 σc=σZ=100 KPa的UU莫尔极限应力圆

同方法一的理由，由于饱和正常固结黏土在同一个剪前孔隙比下(同一个预固结压力σc=100 kPa)，故形成的几个极限应力圆大小相同，位置各异，有效强度包线仅一条，此为水平包线，qu/2=Cu。

方法三：按笔者修正的方法

在试验中对试件模拟地基土实际受力过程：首先，直接让试样在预固结周围压力σc=K0×σZ=K0×σ1=70 kPa作用下预固结，各试件应力状态为同一个点圆，σ3=70 kPa。然后，在排水条件下施加主应力差主应力差q=σ1-σ3=100-70=30 kPa，各试件应力状态为同一个点圆，此时不会剪破，因为其应力迹线是K0线，其应力圆是一个小圆(此即是基底下 5 m深处未加附加荷载时的应力状态)。最后，在不排水条件下施加主应力差qu=σ1-σ3至剪破(此即是基底下 5 m处施加附加荷载后的应力状态)。如此最大限度地模拟了实际的受力过程。

也可近似取试验的预固结周围压力σc=σ3=1/3×σ1+2×σ3=100+2×70=240 kPa=80 kPa(试验状态S1的第1个σ3，S1前缀S表示“试验的”)，即让各试样在此σc=80 kPa排水预固结，此时各试样的应力状态为同一个点圆C。预固结后对各试样分别施加不同大小的周围压力增量△σ3=0 kPa、100 kPa、200 kPa、300 kPa，即σ3=80 kPa、180 kPa、280 kPa、380 kPa，△σ3施加过程试样处于密封不排水状态，即不固结，周压增量△σ3全部由孔隙水承担，此时各试样的应力状态仍为一个个点圆，但位置不同；最后，施加主应力差qu=σ1-σ3至剪破，得到几个极限总应力圆，如图5所示。

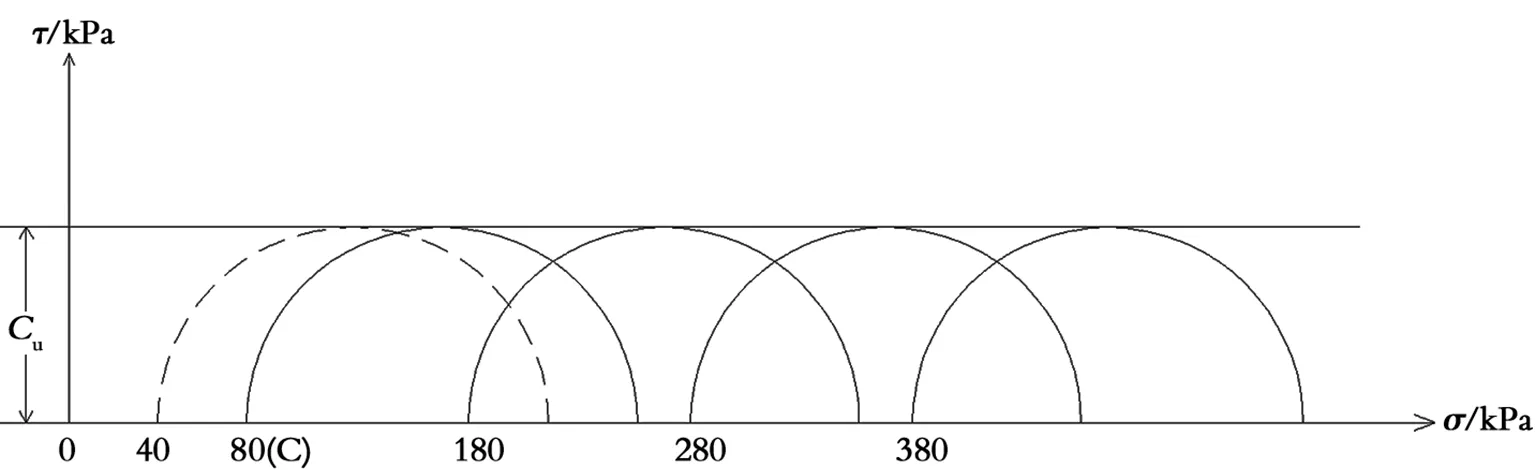
图5 σc=80 KPa(≈K0σZ)的UU莫尔极限应力圆

同方法一的理由，由于饱和正常固结黏土在同一个剪前孔隙比下(同一个预固结压力σc=80 kPa)，故形成的几个极限应力圆大小相同，位置各异，有效强度包线仅一条，此为水平包线，qu/2=Cu。

通过以上分析，对三种试验方法的特点分别总结如下：

方法一：是在σc=0排水预固结，周压σ3全部由孔隙水承担，此时各试件应力状态仍为一个个点圆；最后，在不排水条件下施加主应力差qu=σ1-σ3至剪破，得到几个大小相同的极限总应力圆。

方法二是在σc=100 kPa排水预固结，周压σ3全部由孔隙水承担，此时各试件应力状态仍为一个个点圆；最后，在不排水条件下施加主应力差qu=σ1-σ3至剪破，得到几个大小相同的极限总应力圆。

方法三简化为在σc=80 kPa作用下预固结，周压σ3全部由孔隙水承担，此时各试件应力状态仍为一个个点圆；最后，在不排水条件下施加主应力差qu=σ1-σ3至剪破，得到几个大小相同的极限总应力圆。

3 结 语

通过以上分析，以上3种方法的不同仅在于预固结周围压力σc的不同，其中方法三更符合地基土真实的受力情况——地基土真实预固结周围压力σc=80 kPa。由于方法一的预固结周围压力σc=0小于方法二σc=100 kPa和方法三σc=80 kPa(即地基土真实的附加荷载之前剪前围压)，故其剪前孔隙比也大于后二者，其总极限应力圆直径亦小于后二者，方法一试验结果小于方法三，即较真实情况偏低。同理，方法二试验结果大于方法三，较真实情况偏高。

对方法三试验结果的处理是：每一组3件～4件试样作3个～4个极限应力圆，因其内摩擦角理应为“0”，这几个极限应力圆不应作公切线，而应取各个极限应力圆的平均值qu，再按Cu=qu/2得一个Cu值平均值，以不少于6个Cu值平均值统计标准值。由于不同深度的土层实际所受的预固结压力不同，故即使是同一土质，Cu亦随深度增大而增大。因此，在勘察现场取样时对同一土层，亦应在不同深度取样，且按不同深度的实际压力设定UU试验的剪前预固结压力σc。也就是对同一层土按深度分为几个力学亚层(深度亚层)进行采样和试验，各力学亚层的Cu代表值即标准值是不同的。

对于《地基基础设计规范》1/4b展开深度的地基承载力公式(5.2.5)，规范要求其各项系数按板底下1b内的内摩擦角标准值查表，对于此UU试验值，内摩擦角标准值显然为0，则公式中Mb、Md、Mc三个系数中前两个为0，仅Mc项为3.14。而板底下1b内的Cu标准值如何统计呢？因为筏板下越深处的Cu值越大，笼统地将1b深度范围内不同深度的Cu值进行统计从统计学意义而言也不合理。另一方面，采用公式(5.2.5)由于塑性破坏从基础底部(两侧边)开始逐渐向下开展到1/4b深度(当然涉及更复杂的非线性弹塑性问题，实际没这么简单)，如果按1b深度统计，是将下部较大的Cu值统计进来，而实际上发挥更大作用的是上部的较小的Cu值，从而计算承载力会高于实际承载力，当然，此公式按1/4b展开深度计算承载力本身已含有安全储备却是另一回事。

基于以上分析，如果按板底下1b内的进行计算承载力，则细化为按一倍基宽深度内划分几个力学亚层(深度亚层)，各亚层的Cu按厚度加权平均，较浅部的权重大于较深部的权重，如此统计得到的Cu标准值作为承载力计算参数。