基于机器学习的航班静态四维轨迹预测研究

梁海军，韩琪聪

(中国民用航空飞行学院空中交通管理学院，四川 广汉 618307)

1 引言

静态四维轨迹预测指的是空管部门在航班飞行前对航班飞越航路关键点的时间和高度进行估计。基于航班静态四维轨迹的估计结果，空管部门可以提前预知运行过程中空域单元的飞行流量，同时针对重大活动管制、恶劣天气等因素对相关空域单元的影响，管制部门也可以提前进行航班飞行调配，以提高空中交通的运行效率[1]。同时，航班运行过程中也可以基于静态轨迹估算结果实施飞行计划与雷达航迹匹配、飞行冲突和飞行一致性告警等空中交通关键管理手段。因此精确的四维轨迹预测是保证飞行安全、维护空中交通秩序、提高交通效率和经济性的重要基础。最初的四维轨迹预测方法的基本思想是将整个航班飞行过程分为不同阶段，按不同阶段需要完成的飞行目的建立运动学和动力学方程[2]并求解来完成估算。文献[3]提出了一种基于飞行剖面划分的航班轨迹估算。由于这类预测方法未考虑飞行环境条件变化对飞行的影响，且飞行阶段的没有明确合理划分，因此预测结果误差较大。后续的一些算法引入航空器意图等因素来进行航班四维轨迹预测[4-5]，但该类算法的预测模型较为简单，未能精确的把握航班飞行过程的随机性特点，因此容易造成过拟合使得预测结果波动较大。随着航班运行数据的大量存储[6]，后续的算法引入了历史数据分析来进行四维轨迹估算[7]，文献[8]提出了一种基于数据融合分析的飞行轨迹估算方法。鉴于上述分析，提出了一种在历史雷达或ADS-B(automatic dependency surveillance-broadcast)监视数据的基础上，采用概率统计模型对飞行过程中航班的飞行状态转移关系进行建模，并通过历史数据求解最优模型参数，最后以最大后验概率预测关键点的飞越时间和高度。历史数据中包含了航班历次飞行的航班位置以及环境因素，是被证明了安全、可行和正确的飞行路线。算法挖掘历史数据规律而不必对飞行过程人为划分阶段进行四维轨迹预测，结果更加的精确可信。

2 背景描述

2.1 问题描述

现有的空管自动化系统以时间戳10 s对航空器监视数据进行保存，包含其雷达监视信息、与飞行计划匹配信息、预警告警信息等。在进行模型参数优化之前，需要先对历史数据进行处理，将数据以航班号和飞行日期建立搜索索引，且针对单次飞行的航班数据进行平滑、去噪和插值等预处理[9]，并将所有经纬度信息转换到直角坐标系下。轨迹集采用下式表示：

S={S1，S2，…，ST}

(1)

(2)

其中：式(1)表示按时间保存的原始估计数据，式(2)表示按航班号为j飞行日期为i的航班轨迹，共包含t个位置更新点单个轨迹点包含x、y、z和t等元素，分别代表直角坐标的位置和时间戳。

静态四维轨迹预测主要需要解决以下问题：

1) 建立航班飞行状态转移M，包含未知参数λ={λ1，λ2，…，λk}；

2) 基于历史轨迹运用合适算法(如EM)迭代优化模型未知参数；

3) 基于最优模型预测航班静态四维轨迹。

2.2 模型描述

基于HMM[10]建立飞行过程转移模型，HMM通过描述离散状态动态转移和观测值与状态之间的关系来预测对象未来时刻信息，广泛应用于地面交通“停留位置”预测，包含如下：

HMM={O，Q，A，B，π}

式中：O表示观测值序列，Q表示隐状态序列，A表示隐状态转移概率矩阵，B表示观测概率矩阵，π表示隐状态初始分布。A中元素aij=p(qt+1=j|qt=i)表示当t时刻状态为i时t+1时刻状态为j的概率，B中元素bij=p(ot=j|qt=i)表示当t时刻隐状态为i时观测值为j的概率。HMM具有如下性质(称为马尔科夫性质)：

p(qt|qt-1，…，q1，ot-1，…，o1)=p(qt|qt-1)

p(ot|qt，…，q1，ot-1，…，o1)=p(ot|qt)

在建立HMM模型的基础上，需要解决如下问题[12]：

1) 模型参数学习

(3)

上式为EM迭代算法，迭代过程中未知参数λ(g+1)>λ(g)总是成立，当迭代满足结束条件时的参数λ(g)即为EM算法下的最优参数。公式中O为历史监视数据序列，q∈Q为某一时刻的航班隐状态。

2) 隐状态序列估计

3 飞行状态转移建模

采用HMM对飞行过程建模的关键是对模型参数{O，Q，A，B，π}进行正确合理描述，既能完整的包含观测值和隐状态的所有取值，又能提高算法的效率和预测精度。分别对飞行过程中位置和高度建模，通过位置和高度模型预测经过关键点的时间和高度。文章重点介绍位置建模方法，高度建模类似。

3.1 观测值建模

历史轨迹包含航班飞行时段内按周期更新的位置、速度、航向等信息。若以此离散轨迹点对观测值建模，其数据量较大，且相邻轨迹点属性由于航空器性能限制不会产生急剧变化，因此为简化模型和提高效率，采用固定网格化地图对位置观测值进行建模[11]，固定间隔高度对高度观测值进行建模。

从图1可知，将整个地图分为6×8的相同尺寸网格，从左上到右下分别标记为(1，1)、(1，2)…(6，8)。划分网格之后，航班飞行轨迹就可以使用网格标记序列表示轨迹。如图1中轨迹T即可表示为[(1，1)，(2，2)，(3，3)，(3，4)，(3，5)，(4，6)，(5，7)，(5，8)]。显然，轨迹的观测值序列取决于网格化地图的划分方案，当划分不合理时会导致轨迹描述缺失问题[12]。采用网格化地图对观测值建模需要根据计算量与预测结果精度进行平衡找到最佳参数。当网格尺寸τs(km2)较小时，建模精度高但计算量大；反之，在减小计算量的同时降低了建模精度，对应的高度层间隔参数τh(m)对模型产生相同的影响。建模时仅需对飞行计划航路包络线范围的地图及高度层进行处理。

图1 网格化地图方案示意图

3.2 隐状态建模

本文中HMM隐状态才是对关键点经过时间和高度最直接的描述，但是从历史数据中不能直接获得，因此需要通过与观测值序列建立相应关系进行求解。民航航班须在计划航路范围内飞行，因此位置隐状态集合选择计划航段两侧偏移10 km的矩形区域，同时额外添加停止和偏航2个状态以完整的描述航班位置，图1中qi即为一个航段隐状态。在高度方向上选择标准民航飞行高度层作为高度模型隐状态。在状态转移过程中，取第一次到达某一航路段的时间/高度为预测结果中该航段起始关键点的时间/高度。

针对具体飞行计划，可以通过解析AFTN报文中的航路关键点建立模型隐状态集合。图1中所示的轨迹T包含4个航路隐状态、1个偏航和1个停止状态。

3.3 隐状态转移概率矩阵

隐状态转移概率矩阵描述了各时刻航班位置/高度在隐状态之间转移的概率。航班飞行状态的位置转移的可能性如下：① 当前航路段；② 下一航路段；③ 偏航区域；④ 降落机场(停止)。状态转移之间的关系是可以描述为“有向图”，且包含一个到本状态的转移关系，边上的权值为状态转移概率。高度方向上状态转移包含当前以及相邻的上下高度层。图2描述了各位置隐状态之间转换：

根据图2可知，下一时刻状态依然为当前状态的概率为0.94；为下一状态的概率为0.035；为偏航状态的概率为0.005；为停止状态的概率为0.02。每一隐状态的转移概率处于矩阵同一行，每行概率和为1表明模型列举了隐状态的所有转移的可能性。

图2 位置隐状态转移有向图

3.4 观测概率矩阵

观测概率矩阵描述了隐状态与观测值之间的概率分布关系，本文中观测矩阵的意义是对应某一隐状态的航班位置/高度分布在某一标记的网格化地图区域/高度层的概率。同一观测值与隐状态的转移概率处于同一行，每行概率和为1表明观测值可能为任一隐状态之间存在对应关系。如图1所示，假设t时刻航班处于隐状态q，其观测值概率如表1所示：

表1 状态q的观测值概率Table 1 Observation probability of q

3.5 隐状态初始分布

根据马尔科夫性质简化模型计算时，其中转移概率p(qt|qt-1)和观测概率p(ot|qt)可从模型参数A和B中获取，那么还需要在建模时确定参数是隐状态初始分布p(q1)，本文中即为航班初始位置的分布。由于民航航班在机场跑道起飞，因此模型中位置隐状态初始分布选取以机场跑道起点为中心的圆形区域均匀分布；高度隐状态初始分布选择机场标高为均值的均匀分布，分布的待定参数通过历史数据进行学习优化。

4 静态四维轨迹估算

本章主要针对位置模型简要介绍参数学习和隐状态序列预测相关算法[13]，高度模型类似。

1) 根据原始历史监视数据信息(航班位置序列和飞行计划)完成观测值序列O与隐状态序列Q的建模；

2) 基于航班历史监视数据轨迹集TS学习模型参数，算法通过马尔科夫性质简化后采用EM算法[7]学习模型参数。

3) 在完成模型参数学习之后，根据网格化处理之后的观测值序列求出最可能的隐状态序列。

取状态转移过程中第一次到达某个隐状态的时间/高度作为经过该状态起始关键点的时间和高度；选择监视数据更新周期为预测周期以保证时间预测精度，当更新周期较短时，可以通过前向算法来降低轨迹预测算法的时间复杂度。令

∂i(t)=p(o1，…，ot，qt=i|λ)

(4)

则模型参数迭代优化可简化为：

(5)

按照式(4)的定义，有如下递推关系：

(6)

其中：a、b为模型参数A、B中的对应值，k为模型隐状态数量，因此通过前向算法可将计算复杂度从kT降低到k2T，其中T为预测周期数。

5 仿真实验

本章基于2014年1月1日至2014年12月30日的真实历史监视数据预测某一航班12月31日的四维轨迹为例进行仿真实验[14]，首先针对所有航班数据通过不同的观测值建模参数τs和τh与预测结果精度之间的关系确定建模参数，随后针对任一航班预测结果与传统的运动学、动力学和基于历史数据的回归模型方法的四维轨迹预测结果对比验证本文算法的有效性。首先引入预测结果误差评价因子[15]：

1) 关键点预测误差

2) 累计预测误差：

3) 在航班整个飞行过程中关键点飞越时间/高度预测误差的均值和标准差。

5.1 观测值建模参数

在观测值建模时，选取不同的网格尺寸以及高度间隔进行仿真实验，比较整个航班飞行过程中的经过时间/高度预测均值和方差，以确定最合适的建模参数τs和τh，在预测精度相近的情况下，选择尽量大的τs和τh以提高算法效率。

根据实验结果可知：

1) 关键点飞越时间和高度的预测误差均值都随着网格和高度尺寸变大而变大，但方差总体在一个较为稳定的范围内浮动变化；

2) 由表2可知，预测时间误差均值在网格边长小于 4 km时缓慢增长，超过该值后预测误差均值急速增长，根据“肘部原则”τs选择16 km2(边长为4 km的正方形)；

3) 由表3可知，预测高度均值在高度分层小于30 m时缓慢增长，超过该值后预测误差均值阶梯增长，因此τh选择30 m。

表2 不同网格化方案下的时间预测均值和标准差Table 2 Means and standard variation of predicted time on different gridded cell

表3 不同高度间隔方案下的高度预测均值和标准差Table 3 Means and standard variation of predicted altitude on different altitude separation

5.2 预测结果对比

选取5.1节网格尺寸和分层高度间隔参数进行建模、学习和预测，并与传统的运动学和动力学以及回归模型预测结果进行对比，其算法预测时间误差曲线和算法预测高度误差曲线分别如图3、图4所示。图3中纵坐标所示的预测时间是自航班起飞时刻T0开始的秒数。

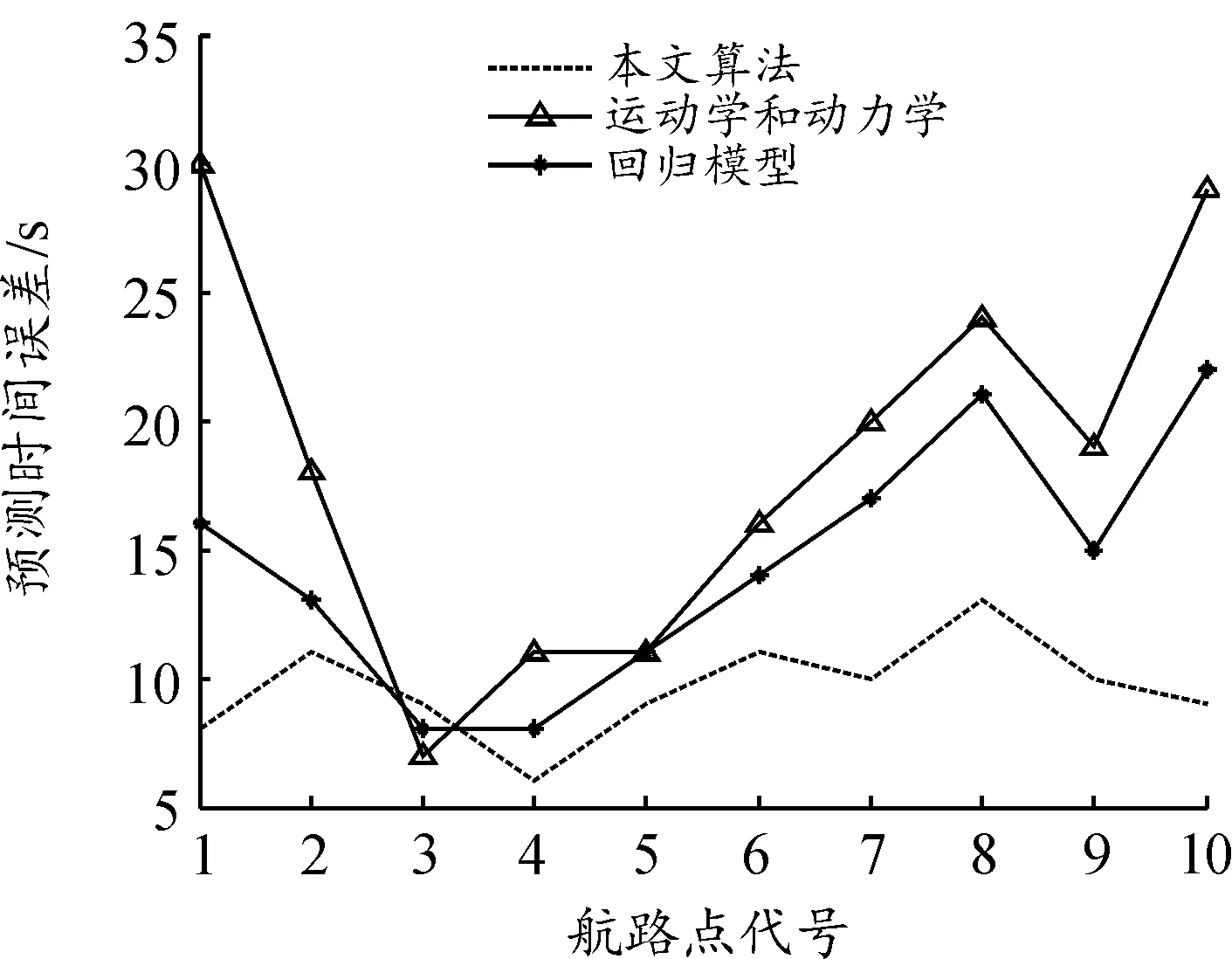
图3 算法预测时间误差曲线

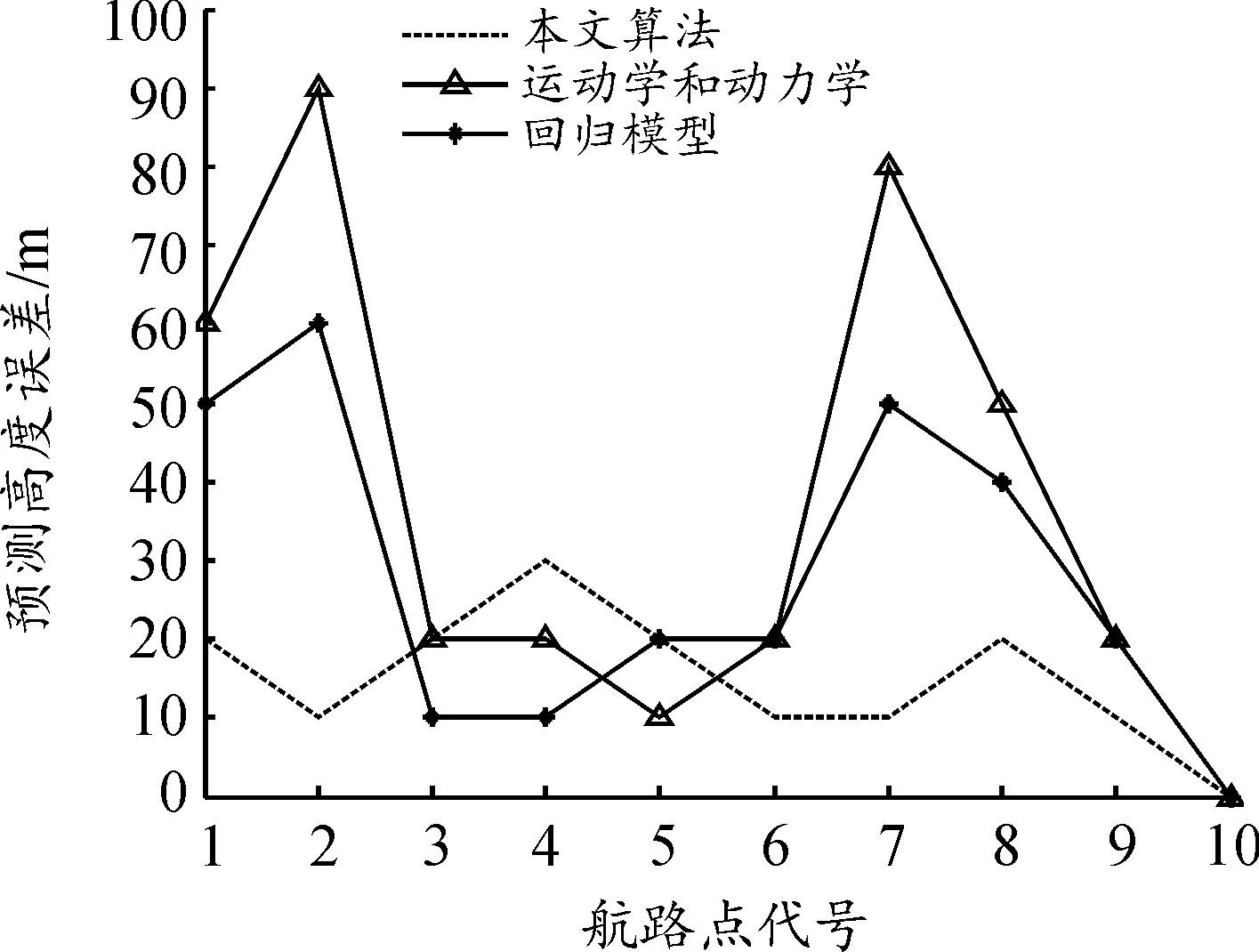
图4 算法预测高度误差曲线

6 结论

1) 与传统的运动学、动力学方法和基于历史数据的回归模型相比：本文提出的方法能更加准确的把握航班历史数据规律，不必对航班飞行过程划分阶段处理；航班飞越关键点的时间和高度预测结果也更精确和稳定。

2) 以本文提出的方法为基础，管制部门实施的调控措施能够提高空中交通运行效率。