两侧小基坑开挖对深基坑围护结构的影响研究

吕金华

（沿海铁路浙江有限公司，浙江 宁波 315012）

1 工程概况

沿海软土地区某大型铁路枢纽改建工程站房共设3层，地下1层，地上两层。地铁2号线铁路南站位于国铁南北通道下方，为地下二层，呈南北走向，属宁波站的地下交通配套工程，与国铁车站一体化共建。

该工程所在场地位于软土断陷向斜盆地中部，地形平坦开阔，地貌类型单一，属第四系冲湖积平原。基坑主要岩性为淤泥质黏性土及黏性土，属典型的软土地基，场地内地下水位埋深0.9～1.2m，受气候影响，水位有一定的变化，但变化幅度不大。

沿海软土地区某大型铁路枢纽改建工程深基坑工程开挖总面积约28000m，国铁南北通道开挖深度10.15m，宽度124m；地铁车站开挖深度20.9～23.7m，宽度40.9～60.2m；地铁结构为地下两层四柱五跨钢筋混凝土现浇结构。基坑安全等级为一级。在深基坑的四个角有四个耳房，耳房中又夹有地铁出入口，耳房基坑最大开挖深度10m，该工程在设计时要求深基坑开挖完成，浇筑底板后，方能开挖两侧小基坑，这样也延长了工期。本文主要研究了若两侧基坑同时开挖，对深基坑围护结构及地基稳定性到底产生多大影响。某大型铁路枢纽改建工程深基坑工程开挖局部图如图1所示。

图1 某大型铁路枢纽改建工程深基坑工程开挖局部图

2 基坑开挖的三维有限元模型的模拟

深基坑工程进行计算分析，因某大型铁路枢纽改建工程深基坑开挖面较大，南北距离长，且南北端头井围护结构形式不同，再加上两侧小基坑不对称开挖，基坑形式复杂。因此，有限元模型应抓住基坑开挖有限元模型的主要因素，建立模型之前应对实际工程做出适当简化。根据工程经验和文献资料，对于深基坑开挖其影响范围宽度一般为挖深的3～4倍，影响深度为挖深的2～4倍。

该工程的基坑开挖有限元模型，取模型宽度为最大开挖深度的约4倍，深度取到⑤1粉质黏土，取南端基坑简化成模型进行分析，模型的基本尺寸为长×宽×高=240m×150m×90m。模型建立的示意如图2所示。

图2 基坑三维模型示意图

2.1 模型单元及边界条件

选做基坑数值计算模型的共设置为921210个单元，314182个节点。基坑边界条件是整体模型的底面约束X与Z方向位移，左右侧边界约束X方向位移，背面约束Y方向位移，由于基坑支撑只取实际支撑的一半，所以在正面施加Y方向位移约束与X、Z方向位移转动约束，立柱桩桩端约束竖直方向的转动。顶面土体施加-1kN/m的超载。

2.2 模型计算的主要参数

2.2.1 土体参数

该工程实际土层数较多，但考虑到将计算模型简化的需要，本文模型将土层性质相近的土层合并，模型计算的具体参数如表1所示。土体设置为三维实体单元。

表1 模型各土层物理力学参数

2.2.2 围护结构

基坑外侧的三轴水泥土搅拌桩设置为水泥土板重力坝，深度为地面下10m范围，厚度为1.5m；国铁通道范围的钻孔灌注桩是有单一的钻孔桩组成，其受力形式与连续墙类似。因此，可以根据其抗弯刚度相等的原则，将钻孔灌注桩等效为一定宽度的地下连续墙形式，进行模型分析。根据相关文献和相关的工程经验表明，将钻孔灌注桩等效为地下连续墙，其结果偏于安全，因此是合理的。按照抗弯刚度相等原则，根据该工程钻孔灌注桩的直径为900mm，间距为1050mm，由刚度相等原则可得：

可得：

通过计算式（2），可得换算连续墙厚度为565mm来建立计算模型。取内地连墙800mm，外地连墙1000mm。围护结构设置为实体单元，通过布尔运算——差集实现与岩土体间的联系，通过匹配面线实现接触面共享。三维模型的围护结构具体参数见表2所示。

表2 围护结构具体参数

2.2.3 支撑等结构

I-1深基坑共设3道支撑，每一道支撑有主撑、斜撑、围檩，第1道支撑还有用于提供施工作业场地的栈桥面板；I-4小基坑开挖深度4m，无支撑，为悬臂结构；由于I-4重力坝区域是地铁出入口，开挖深度14.5m，设2道支撑；I-5小基坑开挖深度9m，上部4.5m为悬臂结构，在4.5m处设有1道支撑；考虑到主撑、斜撑、围檩的截面尺寸差不多，为了方便计算，其单元形式采用线性梁单元，截面统一为1000mm×1000mm混凝土矩形截面，栈桥面板采用500mm厚板单元。

2.2.4 格构柱与立柱桩

I-1深基坑立柱桩—格构柱的截面形式都为四肢角钢格构柱，但截面尺寸不一，但多数格构柱的角钢尺寸为L145×16，缀板尺寸为400×200×10mm，间距600mm，为简化计算模型，格构柱都设置为线性梁单元，且将格构柱都等效为圆形空心钢柱。以下为等效换算方法：

（1）格构柱构件长细比，按下式计算：

式（3）～（4）中：、为构件对主轴x和y的计算长度；i、i为构件截面对主轴x和y的回转半径，其中i=0.43b，i=0.43h。

（2）格构式轴心受压构件的稳定性按实腹式公式计算，但对虚轴x、y的长细比应取换算长细比。四肢组合的角钢构件，其采用的缀件为缀板时，按下式简化计算：

式（5）～（6）中：λ、λ为整个构件对x、y轴的长细比；为分肢对最小刚度轴1—1的长细比，其计算长度取为：焊接时，为相邻两缀板的净距离；螺栓连接时，为相邻两缀板边缘螺栓的距离。

（3）根据抗弯刚度相等原则，角钢格构柱对x、y轴的刚度均相等，则有：

根据式（3）～式（7），并代入相关数据，可以算的等效空心钢柱的直径为600mm，厚度12mm。

I-1深基坑立柱桩—格构柱的形式种类繁多，桥梁立柱桩由20根φ1500，69根φ900的桩组成，最深埋深深度约80m，嵌入圆砾层。

2.2.5 土体本构关系

本跨既有线深基坑有限元模型的土体本构模型采用弹塑性的摩尔-库伦（C-M或M-C）强度理论。

1773年Coulomb针对岩土特性，提出了土体对任何一个受力面上的极限抗剪强度的表达式：

式（8）中：为土体的内摩擦角；σ为土体的受力面上的法向应力；为土的黏聚力。

1910年摩尔（Mohr）提出材料的破坏是剪切破坏，并指出在破坏面上的剪应力是为该面上法向应力的函数，即：

对于此函数，τ=()坐标为一条曲线，叫作摩尔包线。土的摩尔包线通常近似用直线表示，即式（8）表示线性方程。通过简化后的库伦公式表示的摩尔包线的土体强度理论为摩尔-库伦强度理论。

当岩土处于应力空间状态时，此时的摩尔-库伦屈服准则的屈服面为不规则的六角形截面角锥体的表面，如图3所示。

图3 摩尔-库伦屈服面

2.3 有限元模型模拟施工工况步骤

基坑的现场实际开挖工况，结合有限元模型模拟土层开挖，具体设定总体土层为9层，每次开挖一次开挖到位，即钝化该层土，I-1基坑安置3道混凝土支撑。本文数值模拟实际开挖过程共设置10个施工阶段，第一阶段为土层未开挖状态下的围护结构、立柱桩、初始地基平衡状态。MIDAS/GTS模拟实际施工开挖工况的具体步骤如表3所示，第5阶段的模型如图4所示。

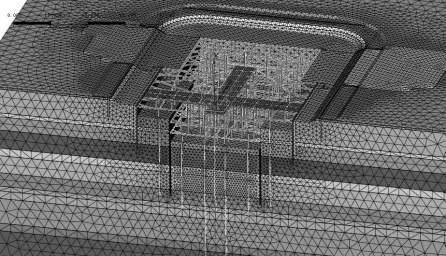
图4 第5阶段的模型图

表3 MIDAS/GTS模拟实际开挖施工步骤

表3 续表

本文数值模拟深基坑和两侧小基坑同时开挖过程共设置5个施工阶段，第一阶段同样为土层未开挖状态下的围护结构、立柱桩、初始地基平衡状态。MIDAS/GTS模拟假定施工开挖工况的具体步骤如表4所示，全部开挖完后的模型如图5所示。

表4 MIDAS/GTS模拟假定开挖施工步骤

图5 全部开挖完后的模型图

3 模拟实际开挖工况下围护结构变形与监测结果

3.1 初始地应力分析

对于深基坑工程，土方的开挖是在土体自重作用下固结沉降完成后开始。对基坑开挖进行前应对自重应力作用下的土体应力和土体位移完成后的原状进行模拟，作为后续施工阶段的初始阶段。建立模型时将土体实体单元和模型边界激活，位移值设置为零，作为自重应力阶段计算。MIDAS/GTS计算模型的土体自重应力平衡如图6所示。

图6 自重应力平衡云图

3.2 围护结构变形分析

该基坑工程最外层为双轴搅拌桩，外侧围护为钻孔灌注桩，内侧为地下连续墙结构。随着深基坑的施工开挖，基坑区域的原有土体平衡状态被改变，而由于存在围护结构等的作用，导致围护结构会随着施工开挖深度的加深而导致围护结构变形。由于基坑内侧土体卸荷，基坑外侧土体会对围护结构产生侧向作用。图7为基坑围护结构三维图。

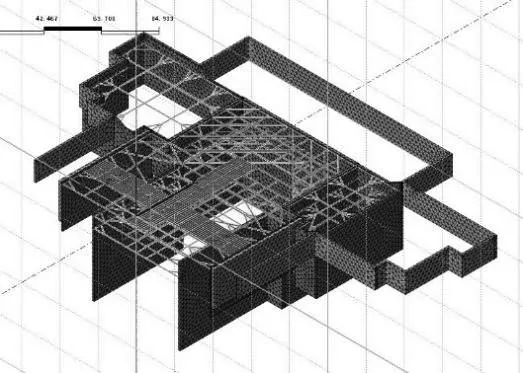
图7 基坑围护结构三维图

3.2.1 模拟实际开挖与假定开挖工况下围护结构变形

经模型分析，在两种不同工况下，I-1基坑地连墙在深基坑开挖到底面后，最大深层水平位移东西侧均约为14mm，整体变形较大在地下连续墙顶面以下约17m处；东西两侧地连墙顶面最大位移约为8mm；南端头地连墙最大深层水平位移在跨中顶面以下约12m处，变形约20mm；基坑围护结构的最大深层水平位移的位置不同，主要和基坑开挖过程中所受超载及支撑位置、地连墙的长度，从而影响墙体的整体刚度所致。在本模型计算中，没有考虑地下水的变化影响，但是在该工程实际监测过程中，水位的变小很小，均在土层面以下1～2m深度处，所以本模型静态情况下，模拟基本合理。

图8和图9为实际开挖计算模型和假定开挖施工工况下的围护结构东侧中部地连墙深层水平位移曲线，图10和图11为实际开挖计算模型和假定开挖施工工况下的围护结构西侧中部地连墙深层水平位移曲线。从这两组图形可以看出，I-1深基坑开挖对地连墙变形的影响较大，特别在基坑开挖的最后一层土更甚，这时地连墙容易达到受力极限状态，开挖时需实时监测地连墙变形情况，从而保证深基坑的安全施工；从这两组图形还可以看出，两侧耳房小基坑的开挖对地连墙变形的影响不大，主要由于小基坑开挖深度不深，对土体平衡影响不大，但是在西侧开挖深度较大的出入口处，还是有一定的影响，施工单位在开挖时应做好充分的施工前分析，保证安全施工。图12为实际开挖工况下南端头地连墙位移图，该处深层水平位移量较大，模型计算达到了20mm，但在实际监测过程中达到了40mm，临近了设计报警值，主要因为该处经常堆放大量建材以及停放大型机械设备，施工荷载很大，基坑边上尽量不要堆放建材，大型施工机械要与基坑围护结构保持一定距离。

图8 实际开挖东侧地连墙位移图

图9 假定开挖东侧地连墙位移图

图10 实际开挖西侧地连墙位移图

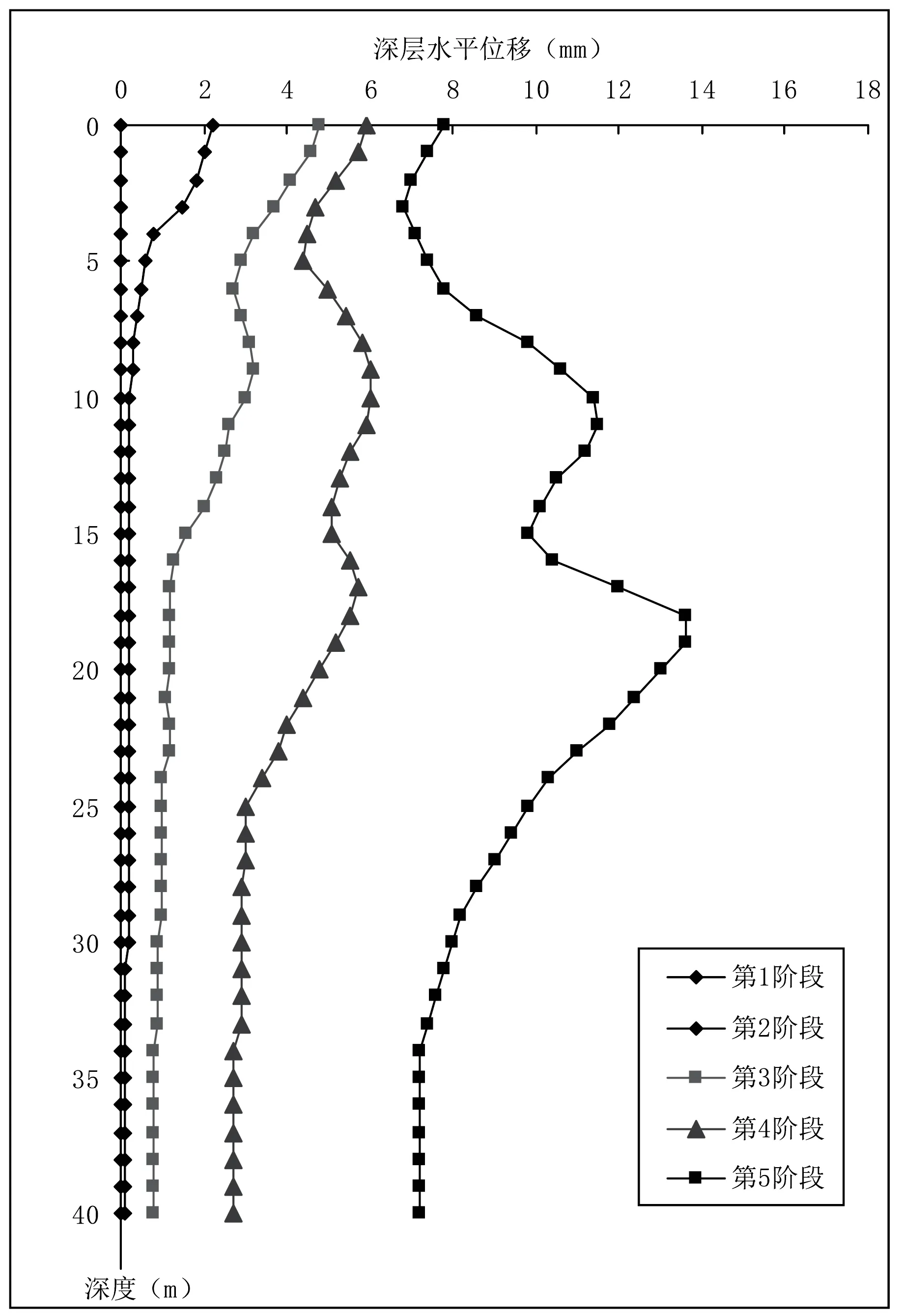
图11 假定开挖西侧地连墙位移图

图12 实际开挖南端地连墙位移图

3.2.2 模拟实际开挖与假定开挖工况下支撑轴力

从图13和图14可以看出，各道支撑轴力均随着基坑开挖深度的增加而增加，当第二道支撑安置后，第一道支撑轴力基本稳定，无明显增长变化，当第三道支撑安置后，第二道支撑轴力无明显增长变化，其中第一道支撑轴力最大值为-2180.56kN，第二道支撑轴力最大为-2580.23kN，第三道支撑轴力最大约-3810.41kN。小基坑开挖时能轻微的释放I-1深基坑支撑轴力。小基坑的开挖时，I-5支撑支撑轴力最大值为-1341.64kN，I-4重力坝第一道支撑支撑轴力最大值-782.05kN，I-4重力坝第二道支撑支撑轴力最大值-1591.11kN。

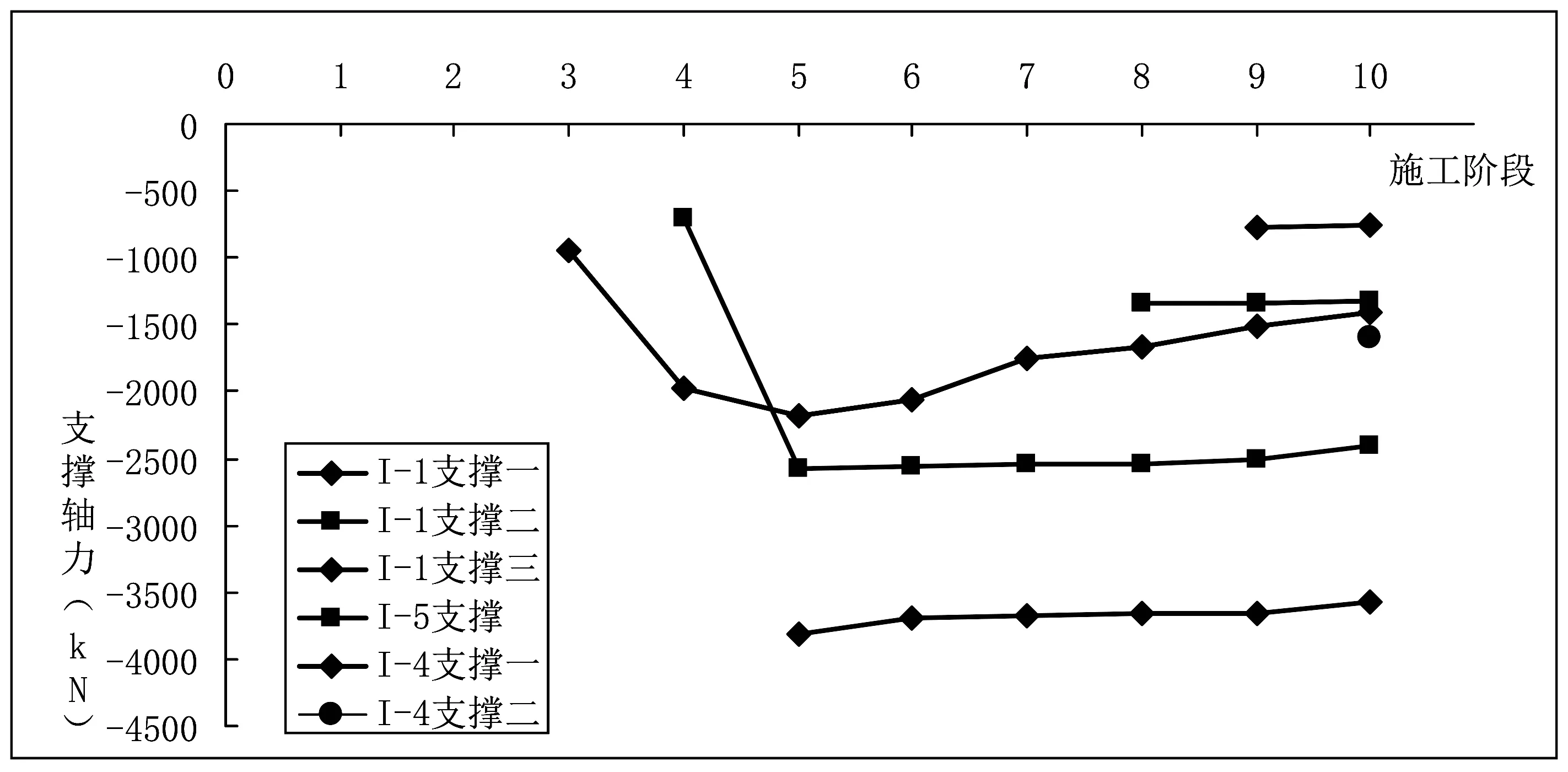
图13 实际开挖最大支撑轴力

图14 假定开挖最大支撑轴力

表5所示为基坑支撑开挖模拟计算最大值与最大监测值、最大设计报警值对比，从表中可以看出，I-1基坑支撑最大监测轴较计算值大的有第一、二道支撑，第三道支撑最大监测值较计算值小；而各道支撑设计轴力安全系数相对较高，其比值均小于0.5，说明支撑的设计偏于安全。最大计算支撑轴力与监测轴力的比值在0.7～1.2，模型还是比较真实地反映了实际工程。

表5 水平支撑轴力开挖模拟计算最大值与最大监测值、设计报警值对比

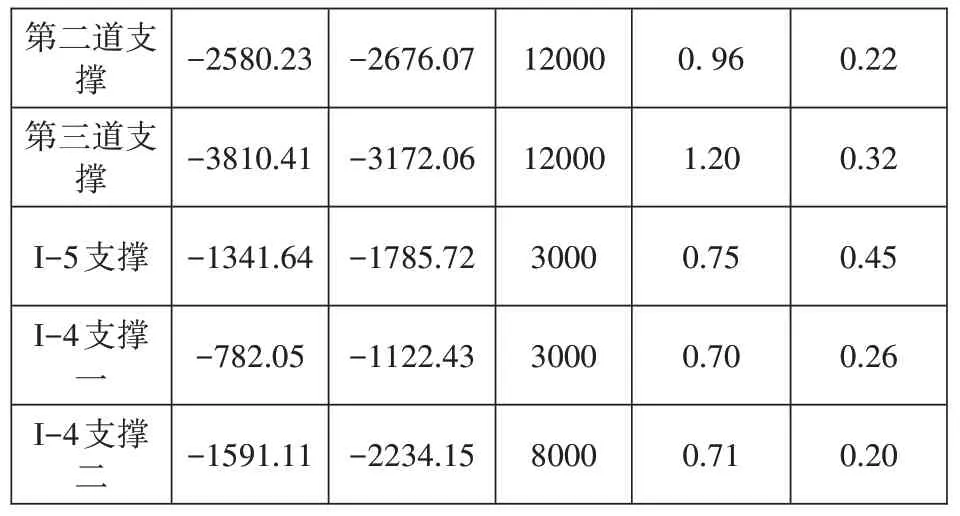
表5 续表

4 结语

由模型分析数据可知，两侧小基坑同时开挖有利于释放I-1深基坑东西两侧土压力，反而减小深基坑围护结构深层水平位移和支撑轴力，但是两侧小基坑开挖深度较小，且每个小基坑内的地铁出入口，由于出入口开挖深度较大（约为15m），出入口施工时要凿开深基坑地连墙与深基坑相通，待出入口施工完成后，两侧耳房小基坑才能进行下一步施工，所以必须在深基坑下部结构都完成，保证深基坑围护结构的稳定后，才能进行出入口的施工，否则无法控制深基坑围护结构的安全稳定。两侧小基坑与深基坑同时开挖，坑内结构物也无法同时完成，从而无法缩短工期，并且导致施工作业面紧张，施工混乱，管理困难，容易造成安全隐患。所以在深基坑开挖完成后再开挖两侧耳房小基坑较为合理。