基于不完全信息博弈的电能交易商电能交易战略决策方法

张琳娜，柳永妍，李昊炅

(1.国网山西省电力公司，山西 太原 030001；2.国网湖南省电力有限公司电力科学研究院，湖南 长沙 410007)

0 引言

我国在《关于进一步深化电力体制改革的若干意见》(中发〔2015〕9号文)中明确要求“开放售电侧，多途径培养市场主体”，允许五类主体参与售电业务，单独核定输配电电价。将市场竞争引入售电侧，推进以完全充分竞争为特征的市场开放自由化进程是未来区域电网的大势所趋[1]。这其中需要建立主体多元、份额平衡、有序竞争的售电侧市场化格局，使电价能够有效反映其成本和合理利润，还原电力的商品属性。

高渗透率分布式电能资源(Distributed Energy Resource，DER)接入区域电网运行为实现售电侧市场化所要求的“多买多卖”格局提供了重要途径和手段[2]。文献[3]提出了含高渗透DER的区域电网市场化运营模式，设计了基于电能管理计划的能量管理流程，并指出合理有效的电能交易战略对于提高该运营模式中市场交易主体的经济效益至关重要。

目前售电主体竞争交易策略主要可分为三类:预测交易时段的市场清算电价(MCP)的方法；利用交易市场公开发布的信息估计竞争对手竞价行为的方法以及基于博弈论的方法。文献[4]通过借鉴发电侧最优竞价策略，采用预估对手竞价行为的方法对售电市场竞价策略进行了仿真分析。文献[5]将多供电公司之间的多人不完全信息博弈问题转化为双人博弈问题，给出了基于Stackelberg博弈的供电公司最优竞价策略。发电侧交易竞争主要有如下三类方法:基于博弈论的方法；基于优化规划理论的分析方法和基于人工智能的方法[6]。文献[7]针对发电侧竞争博弈方法进行了研究，分析了低谷和高峰竞价下不同容量发电厂商的市场竞争力，比较了纳什均衡点电价与统一清算电价的偏差。

现有电力市场竞价策略的研究仅单一考虑售电侧或发电侧，属于单边竞争策略，在发电侧开放的基础上进行售电侧市场化需对双边市场竞价战略进行研究。本文以文献[3]所提出的区域电网市场化运营模式为基础，对其中的电能交易商的电能交易战略进行研究。基于售电侧市场零售电价和发电侧电厂边际电价与负荷的关系建立电量电价模型，根据发电厂商和负荷类型确定相应的可靠性电价，在可靠性电价的基础上采用营销学中反向定价的方法确立电能交易商的战略方案，基于不完全信息博弈论对电能交易商采用不同战略方案的产量和收益进行算例分析。

1 区域电网市场化运营模式

文献[3]提出的区域电网市场化运营模式是基于高渗透率分布式电能资源接入运行的现实，以分层汇聚的方法形成多个电能交易商，参与售电侧的市场竞争，图1为文献[3]提出的区域电网市场化运营模式的组织结构。

图1 区域电网市场化运行模式的组织结构

交易商在电力市场中承担汇聚电能、交易电量的职能。交易商利用以电价为主的动因刺激手段在发电侧交易平台上依据电能资源的不同类型和系统负荷需求分时段发布交易计划，吸引各类电能资源参与，同时，也在售电侧交易平台上依据负荷变化分时段发布交易计划与外边电力市场进行交易，获取优质用电用户。因此，交易商的获利主要来源于售出价与购入价的差值，制定合理的战略方案来确定交易计划成为电能交易商的首要研究问题。

2 电能交易商交易战略制定

电能交易商将从发电厂商处购买来的电能销售给用户，通过赚取其中的差价来盈利。电能交易商需充分掌握发电方售电和购电方购电的电量电价模型，在此基础上建立电能交易商购售电交易战略。设电能交易商i的战略集合为M)，B(G，E，N))}，j=1，2，…；每个战略zj取决于如下信息:面向用户的售电侧交易战略S(P，Q，M)，以及面向发电厂商的购电侧交易战略B(G，E，N)。

2.1 售电侧交易战略

售电侧交易战略S(P，Q，M)，取决于如下信息:售电市场价格P，电能交易商为不同容量等级用户设定的分级电价或电价批零差价率组合Q以及各容量等级用户市场所占比例组合M。

对于用户，商品的价格对其需求量有直接的影响，通常用需求函数表征商品需求量随价格变动而变动的模型。需求函数是指其他条件相同时，每一价格水平上买主愿意购买的商品量，可表示为:

式中，D表示商品需求量；P表示商品价格。

相应的逆需求函数为:

对于电力市场而言，市场电价与电能销售量多成线性关系，其函数表达式可利用历史交易数据统计得到。利用需求函数获得一定电价下市场的电能需求量，即用户购电的电能逆需求函数为:

式中，P为市场售电电价；q为交易电量；α、β为依据供求曲线确定的常数系数。

针对不同类型负荷，根据负荷的缺供电量(Energy Not Supplied，ENS)[8]，确定各类负荷的可靠性电价。

系统的平均缺供电量指标为:

式中，λk为负荷k的缺供电量指标；Lk为各负荷的负荷数。

各负荷可靠性电价Pk(λk)为:

式中，1＜ξ＜2，μi表示用户k的电价可靠性系数，当λk＜λ0时，Pk(λk) ＞P；当λk=λ0时，Pk(λk)=P；当λk＞λ0时，Pk(λk)＜P，这表明相同可靠性的负荷对应相同的价格浮动准则。当λk＞ξλ0时，为了保证电能交易商的基本利益，规定P0min为最低可靠性电价。

在各类负荷可靠性电价的基础上，对于不同容量的用电负荷，采用营销学中的反向定价法[9]，以可靠性价格Pk为基础，根据负荷用电容量等级确定对其的售电电价，即:

式中，qa为考虑负荷类型的不同容量等级用户的分级电价；a表示用户容量级别；ra%为向各容量等级用户售电的电价批零差价率。若其战略为通过低价吸引大容量用户，则可增加大容量用户的电价批零差价率，减小小容量用户的电价批零差价率，例如对小容量零售用户其电价批零差价率可设为0。因此电价组合Q可表示为Q={qa}或Q={ra}。

各容量等级用户所占比例组合M={ma%}可根据历史统计数据获得，其中ma%为a级用户占比。

2.2 购电侧交易战略

对于发电侧电能交易商而言，一般采用系统边际电价作为各发电厂商的报价基础。系统边际电价[10]是指在现货电能交易中，按照报价从低到高的顺序逐一成交电量，满足负荷需求的最后一个电能供应者的报价。在区域电网市场化运行模式中，电能交易商可基于历史交易数据，采用例如线性回归等方法建立发电侧售电边际电价与系统负荷的关系，可表示为:

式中，G为发电侧售电边际电价；q为交易电量；本文中认为电能交易商购售电电量相同；δ、γ为根据历史数据确定的常系数。

购电侧交易战略B(G，E，N)取决于如下信息:发电侧售电边际电价G，即取为发电侧系统边际电价，电能交易商为不同容量等级发电厂商设定的分级电价或电价批零差价率组合E以及各容量等级发电厂商所占比例组合N。

考虑电能的商品特性，针对不同的发电形式，根据系统出现的功率缺额s的失负荷价值(the value of loss load，VOLL)，确定交易商购电侧各类发电厂商的可靠性电价[11-13]。

式中，V(s)为失负荷价值；s为缺出力量；ε为电力需求弹性系数，取0.23。

根据不同发电形式出力的概率分布，联立式(8)可计算发电商实际输出功率的电价可靠性系数:

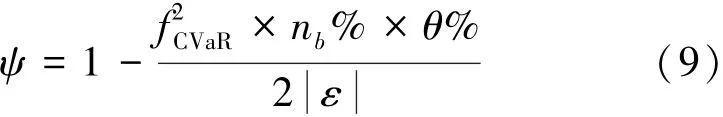
式中，nb%为b级发电商市场占比；θ%为该发电形式发电量的市场份额占比；fCVaR为风险缺额因子，可由发电机组的实际输出期望和最大缺额输出期望得出。

则发电商的可靠性电价Gl可以表示为:

在确定各类发电厂商可靠性电价的基础上，为尽可能多地汇聚不同容量等级的电能资源，采用与售电侧类似的反向定价方法，依据各发电厂商容量级别，以可靠性电价Gl为基准设计分级电价，即:式中，eb为从不同容量等级发电商购电的电价；b表示发电商容量级别；hb%为向各容量等级发电商购电的电价批零差价率。若其电能汇聚目标为大容量发电厂，则可给大容量发电商较小批零差价率，使其成交电价接近该类发电商的可靠性电价，给小容量发电商较大批零差价率或给出高于可靠性电价的报价。反之，若其电能汇聚目标为小容量发电厂，则可主要针对小容量级别发电厂给予较小批零差价率。因此电价组合E可表示为:E={eb}或E={hb}。

同样，各容量等级发电厂商所占比例组合N={nb%}可根据历史统计数据获得，其中nb%为b级发电商市场占比。

2.3 交易商电能交易战略

双边市场下电能交易商电能交易战略如图2所示。

图2 电能交易商交易战略模型

在售电侧，电能交易商i需根据各级用户占比组合M和市场电价P，确定方案j下的电价批零差价率组合Qj，形成售电侧交易战略；在购电侧，需根据各级发电厂商占比组合N和边际电价G，确定方案j下的电价批零差价率组合Ej，形成购电侧交易战略，进而形成交易商i的双边市场交易战略组合Zi。

3 基于博弈论的电能交易商战略方案

在区域电网市场化运营模式下，一级电能交易商通过在电能交易平台内发布购售电的电能交易计划，实现最大化自身经济收益的目标。在制定各自电价策略后，需要与战略未知的其他交易商进行战略博弈，以确定利益最优的战略方案组合。

3.1 不完全信息静态博弈

按参与人行动的先后顺序，博弈可划分为静态和动态博弈两种，按参与人对其他参与人的特征、战略空间及支付函数的知识可划分为完全信息博弈和不完全信息博弈，具体分类见表1[14]。

表1 博弈分类及对应的均衡概念

本文中的各个电能交易商同时在交易平台上发布电能交易计划，彼此无法获知对手的战略方案，只能通过对历史数据的统计，得出对手选择各战略方案的概率，因此交易商之间的博弈属于不完全信息静态博弈。

对于交易商而言，其获利取决于电能的售量与售价，电力市场中成员在同一市场内进行电能交易，作为商品的电能是同质的。对于同质产品，若交易商采取价格竞争的方式提升自身收益，则即使只有两家企业的垄断行业也可实现完全竞争，所有产品只能按边际成定价，企业将无法获利，此即伯川德悖论[15]，故电力市场中采用价格博弈是不可行的；若交易商采用售量竞争的方式提升自身收益，则需依据市场规律建立售购电价与售购电量的函数关系，并设立不同的战略方案与其他交易商进行博弈，此即不完全信息库诺特模型[16]。

3.2 单边多战略博弈

单边多战略场景是指交易商只需在售电侧与购电侧中的一侧进行博弈。以售电侧博弈为例，各交易商针对不同容量等级的用户采取不同的批发电价，发电侧则采用固定成本的模型。以两交易商售电侧市场竞争为例，根据售电侧市场逆需求函数，可得市场电价与交易电量的关系为:

式中，α、β为逆需求函数的常数系数；q1、q2分别为交易商1、2的交易电量。

将市场用户分为4级，根据式(4)获得各战略中a级用户电价qa，结合市场中各容量等级用户所占比例组合M和用户电价可靠性系数，交易商i的战略可以表示为:

式中，ma为a级容量用户市场占比；μx表示x类用户对应的电价可靠性系数。

为获得最大收益，交易商i的期望利益函数为式中，为交易商i的战略方案j，F是对手选择各个战略方案概率的组合。以交易商售电侧均具有两种战略方为例，博弈中两交易商均无法获知对方的准确战略，但对方对各个战略的选择概率是公共信息。若交易商1采用战略，则其期望利益函数为:

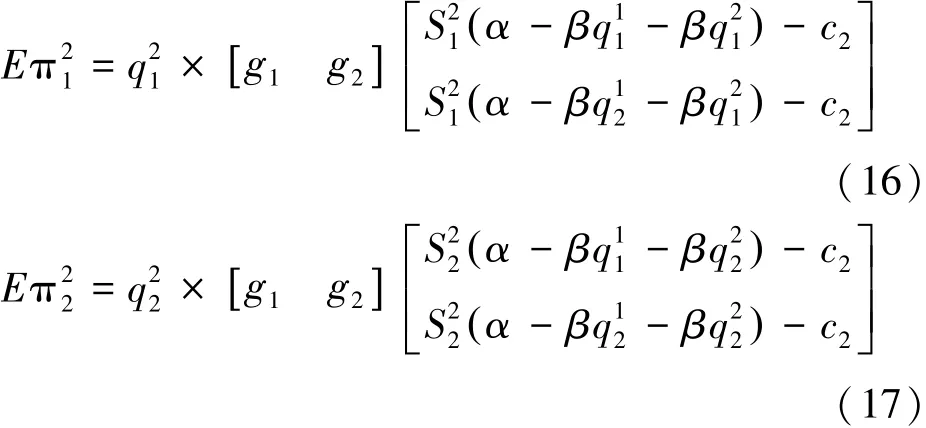
式中，矩阵g= [g1g2]为交易商1选择两种战略方案的选择矩阵；c2为交易商2购电成本。

对以上四式求解最优化一阶条件，可得交易商1的反应函数为:

交易商2的反应函数为:

3.3 双边多战略博弈

双边多战略场景是指，交易商需同时考虑售电侧与购电侧的竞争，针对用户和发电厂分级制定批发电价，确定各交易商自身的战略方案并与其他交易商进行博弈。

以市场中具有两个交易商为例，售电侧市场逆需求函数为P=α-β(q1+q2)，购电侧系统边际电价与系统负荷函数为G=δ+γ(q1+q2)。考虑用户电价可靠性系数μ和发电商电价可靠性系数ψ，交易商i的战略集合为E，N))}，j=1，2，…。

同理交易商1采用其他三种战略以及交易商2采用各战略时的最大化期望利益函数均可表示为式(20)的形式。

对八个期望利益函数表达式求解最优化一阶条件，即可得到交易商1、2的反应函数。联立八个反应函数即可解得双边多战略模式下，两交易商博弈的贝叶斯纳什均衡解:和从而得到各战略下交易商的最优交易电量。

4 算例分析

参考文献[17]和[18]中售电侧逆需求函数和购电侧边际电价-负荷函数为:

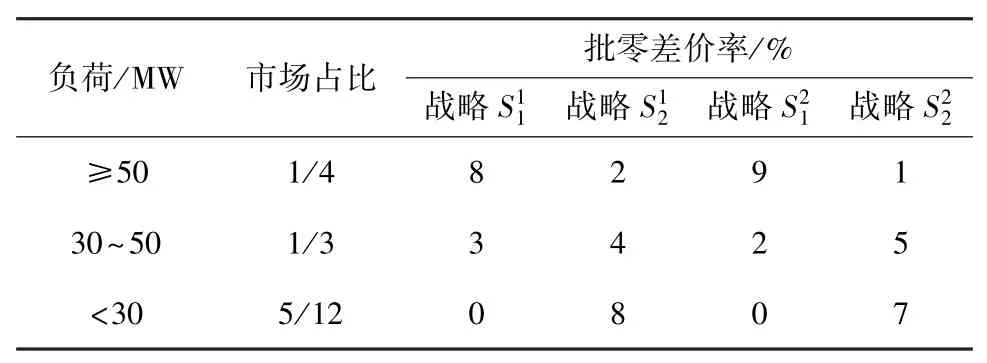
表2 售电侧战略方案

考虑各个容量等级用户在市场中的占有率，各战略可表示为:

表3 购电侧战略方案

将结果代入最大化期望函数可求得各个战略组合下交易商的预期期望利益，见表4。

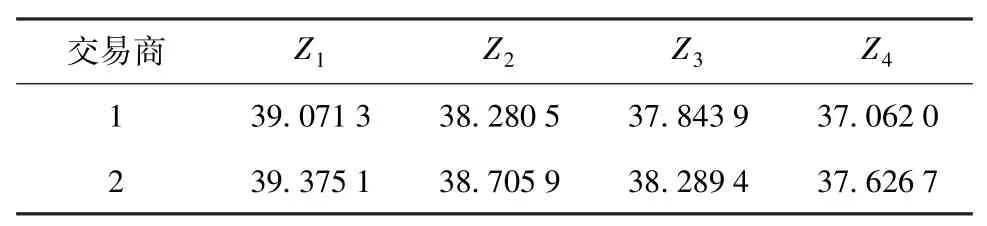
表4 各方案下交易商期望收益

5 结语

本文基于含高渗透率分布式电能资源的区域电网市场运营模式，对电能交易商的电能交易战略博弈策略进行了研究。基于所建立的购售电侧电量电价模型，采用反向定价法建立电能交易商可行的战略方案，给出单边和双边不完全信息博弈场景下交易商的电量博弈策略，通过博弈计算获得的纳什均衡点为交易商选定战略方案提供依据，具体算例分析验证本文提出方法的正确性和有效性。本文为售电侧市场化改革背景下电能交易商交易战略制定方法提供参考。