一种基于动态可重构阵列的矩阵求逆算法实现方法

杨苗苗，郭 锋，李向东，张永亮

（陆军工程大学军械士官学校，湖北 武汉 430070）

MIMO（multiple-input multiple-output）技术[1]作为当前无线通信领域的关键技术之一[2]，可以在提高通信系统的传输速率、提升通信系统的传输质量的同时，不增加额外的带宽消耗。在未来的通信发展中占据越来越重要的地位[3]。

MIMO接收机的一个关键特性是它依赖矩阵运算，包括矩阵乘法、矩阵加法和矩阵求逆[4]等。例如，在MIMO接收机的检测模块，迫零（Zero Forcing，ZF）检测算法[5]、最小均方误差（Minimum Mean square Error，MMSE）检测算法[6]、基于MMSE的并行干扰消除（parallel Interference Cancellation，PIC）检测算法[7]等的核心算法之一都是矩阵求逆运算。传统的矩阵求逆算法是在按顺序执行的微处理器上实现，他们的效率，特别是实时应用程序的效率无法满足当前的性能需求。为了提高性能，文献[8]研究了高阶矩阵求逆的超大规模集成电路（Very Large Scale Integrated circuit，VLSI）阵列架构，虽然ASIC架构可以显著提高性能，但是，显而易见的，ASIC主要是刚性结构，灵活性差。为此，一种高灵活性、高性能的粗粒度动态可重构体系结构[9]被提出。

目前最常用于处理矩阵求逆运算的算法有基于QR的矩阵求逆、伴随矩阵求逆以及基于LU的矩阵求逆等。其中，伴随矩阵求逆的运算过程因包含伴随矩阵和矩阵模求解而显得复杂又繁重，应用中一般不采用；QR分解求逆和LU分解求逆运算的基本思想相似，都是通过高斯消元将矩阵变换为上下2个三角矩阵，通过对子矩阵求逆最终获得原矩阵的逆。但是QR分解运算在硬件上要求定制[6-10]，且其并行计算能力相比LU分解法更弱。综合硬件架构和算法特性考虑，本文针对LU矩阵求逆运算提出了一种基于动态可重构阵列的高效、可扩展的实现方法。通过对算法子数据流特性的分析，针对每个子算法的特性设计各自的映射方案，并将其映射到可重构架构中。该映射结构提高核心算子可重构计算阵列流水效率，增加互连拓展的灵活性，减少硬件开销，增加资源利用率。

本文剩余部分的结构如下：第一节主要介绍矩阵求逆算法的原理，分析归纳其数据流特征；第二节介绍了可重构平台及其具体阵列结构，通过对数据流的分析，将矩阵求逆的运算过程映射到该可重构阵列中；第三节将本文的矩阵求逆实现方案与现有方案在性能、灵活性等方面进行了对比与分析；第四节对整个工作加以总结。

1 矩阵求逆核心算子数据流特性分析

1.1 矩阵求逆算法分析

LU分解求逆运算分为3个步骤，首先对矩阵Ann进行高斯消元，经过一系列变换，将其表示为上三角矩阵U和下三角矩阵L的乘积。然后对A进行求逆运算，其过程包含三角矩阵求逆以及三角矩阵乘。下面对这3个步骤进行一一分析。

1.1.1 LU分解

LU分解数学公式如下：

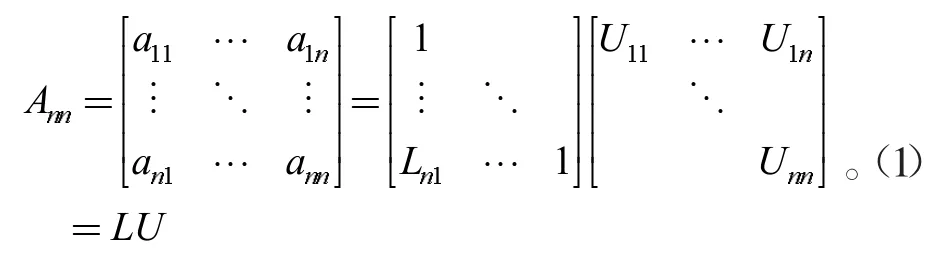
首先，对a11同一列下方数据进行消元，再以a22为列主元，对已消元的矩阵进行第二列消元，以此类推，将本次消元得的矩阵作为下次消元的主矩阵进行消元，重复操作直至运算完成。

对于消元过程中的除法运算来讲，其运算周期较长，消元基行与消元系数相乘的运算过程中存在数据等待现象，因此需要将消元系数复制多份，及时地传输至其需要的多个计算单元中。而LU分解过程中同列消元元素之间的运算并没有直接的数据关系，因此可以并列执行。

1.1.2 三角矩阵求逆

设下三角矩阵L的逆矩阵为R，那么矩阵L求逆的公式如下：

相对应的上三角矩阵U的求逆公式如下：

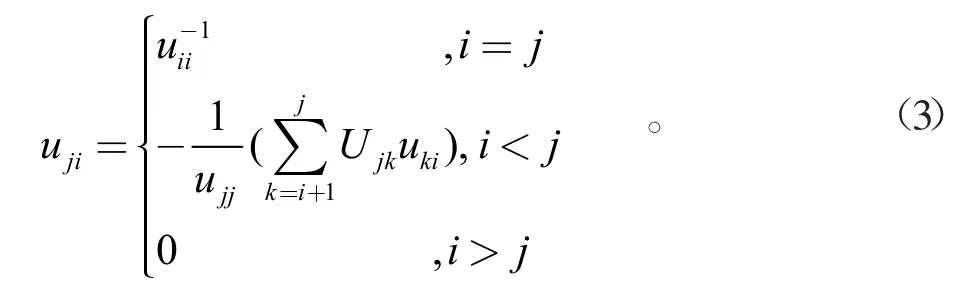
从公式（2）、（3）可以看出，同列元素之间数据关系紧密，比如在求rji时，必须知道其上列的所有元素，也就是执行循环时必须从上至下，但同行元素可并列执行。

1.1.3 三角矩阵乘

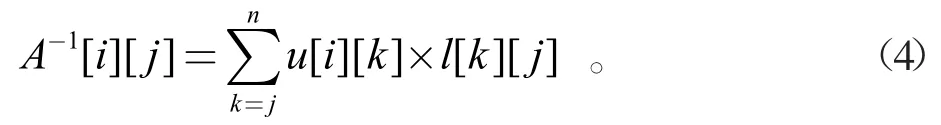
由公式（4）知，A的逆矩阵是由U和L的逆矩阵相乘得来，U的逆矩阵逐行与L的逆矩阵相乘，则得出A的逆矩阵的每一行元素，如此循环迭代出所有元素。从理论层面来讲，若不考虑硬件资源的占用，矩阵U的一行元素可同时与矩阵L的所有列元素并行执行乘法运算，大大提高了数据流水线以及并行运算度。

1.2 矩阵求逆数据流分析

如图1所示，在矩阵求逆数据流运算的3个步骤中，涉及3种运算类别。在矩阵LU分解和三角矩阵求逆阶段计算均由除运算、乘运算、加运算构成；三角矩阵乘阶段则由乘和加运算构成。

图1 矩阵求逆数据流

这3个运算阶段有相同的计算类型单元，将这些单元聚集区称之为域，则LU分解求逆矩阵的数据流具有以下特征：域内数据计算传输具有单向规整性，批量数据并行传输；而域间数据流的运算层次结构不一，数据流水的传播具有发散性或者收敛累和传输。

2 可重构平台介绍及矩阵求逆算子映射

2.1 RASP架构介绍

本文将矩阵求逆算法映射到可重构处理器系统架构RASP之中。RASP的整体架构如图2所示，RASP可重构系统由3部分组成：一是为可重构阵列提供运算的数据存储部分，包括常数和共享存储器；二是可重构阵列，作为RASP架构的核心部分，主要完成阵列计算，通过可重构单元间的互连，形成高效流水线运算模式，将送入阵列数据处理完成后送回存储单元；三是配置部分，根据使用场景向数据存储部分和可重构阵列提供配置信息。

图2 RASP整体架构

在可重构处理器系统中，包含4个结构完全相同的可重构阵列（Reconfigurable Compute Array，RCA）。可重构阵列的基本结构框图如图3所示，每个RCA主要包括4个部分：输入输出FIFO，配置输入寄存器，临时数据寄存器以及计算单元阵列（Processing Element Array，PEA）。

图3 RCA结构图

PEA阵列的具体运算结构如图4所示，其中除法阵列在首行，包含8个除法子阵列，可以并列执行运算；通用计算阵列是6*8规模的二维阵列，可应用于诸多场景计算如LU分解和三角矩阵求逆；累加阵列为2*8规模的二维阵列，是通用阵列的协处理阵列，主要作用是完成大量数据的累加运算。累加阵列与通用阵列协同完成运算，并行度高，且不占用过高的硬件资源。本文的矩阵求逆算子主要是映射在PEA阵列结构中。

图4 PEA阵列结构图

2.2 核心子算子映射方案

2.2.1 LU分解映射

一般情况下，随着矩阵阶数的增大，运算中所需硬件资源也逐步增大。而RCA中的硬件资源是有限的，因此当处理阶数高于阵列PEA数量的矩阵时，必须对计算任务进行切割处理，以适应阵列的大规模运算需求。

本文采用行列式分块顺次映射的方法，以96阶矩阵为例，将计算划分为3个模块，首先，将3个96*32的子矩阵一一映射到3个RCA上，此时每行数据一次性即可完成映射。再切割96*32的矩阵成4个24*32的子矩阵，映射到4个RCA上单独完成计算，且同一列的4个子矩阵可实现并行计算，那么切割后的矩阵如公式（5）所示：

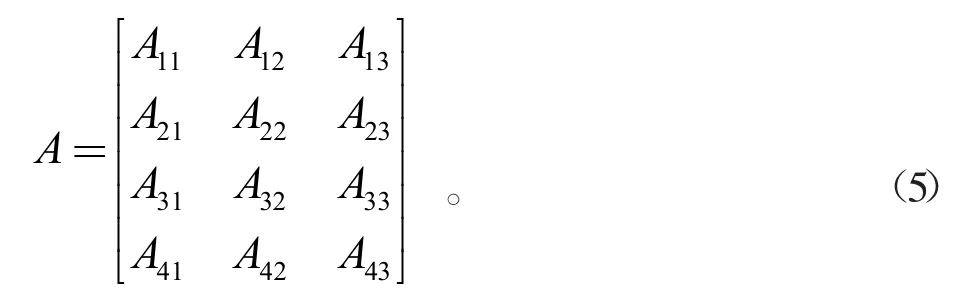
将按行切割的4组数据一一映射到RCA0到RCA3进行计算，例如第一行[A11A12A13]3块数据在RCA0内经行消元计算，第二行[A21A22A23]3块数据在RCA1内经行消元计算，以此类推。在行列式分块顺次计算矩阵LU分解计算过程中，遵循逐列消元、逐行计算的原则进行。单个阵列的映射图如图5所示。

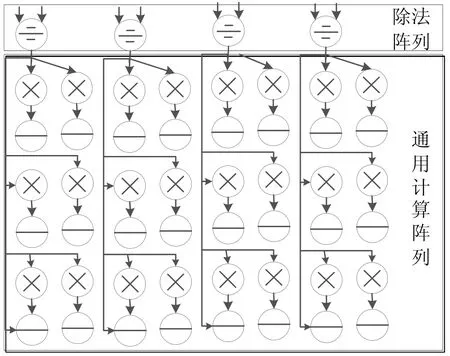
图5 行列式分块顺次计算矩阵LU分解

2.2.2 三角矩阵求逆映射

由三角矩阵求逆迭代运算分析可知，其紧密的数据关系要求运算必须逐行进行。三角矩阵求逆运算过程如图6所示，为了维持最高的并行计算度，从主对角线元素开始，依次向内逐行求解次对角线元素。对于第n行对角线而言，待求元素共97-n个，每个元素上方共有n-1个元素，因此对于求解第n行每个元素而言需要n-1组乘、n-2次加以及1次乘系数。

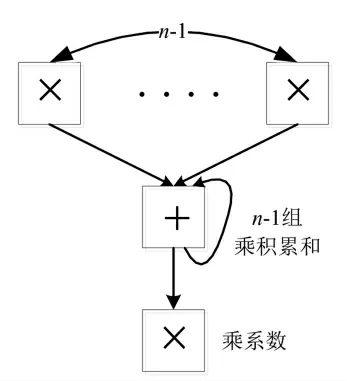
图6 迭代计算三角矩阵逆矩阵元素

数据映射如图7所示，将通用计算阵列分为上下2个区域，这2个区域包含相同的运算单元。1个基本计算单元包含2个乘法运算和1个乘积累加运算。这样相同的上下运算区域将数据流分成了两级流水，流水运算过程有2个特点，一是运算过程中先进行乘法运算，不存在中间值传输阻滞问题；二是采用单个PE循环计算同一个元素，因此即使上下区域内每一个PE接收数据不同步，也不影响最终的结果。

图7 三角矩阵求逆映射

最后，当累加阵列完成运算后，将和传输至乘单元中进行乘系数操作，前后数据运算等待时间仅为（A+T）cycle。该映射方法并行度高，同时采用的流水快速，可以更高效地解决三角矩阵求逆。

2.2.3 三角矩阵相乘映射

三角矩阵相乘相对简单，采用常规的乘法和累加单元即可，如图8所示。其中，累加阵列的结构与PEA内累加阵列结构相同。

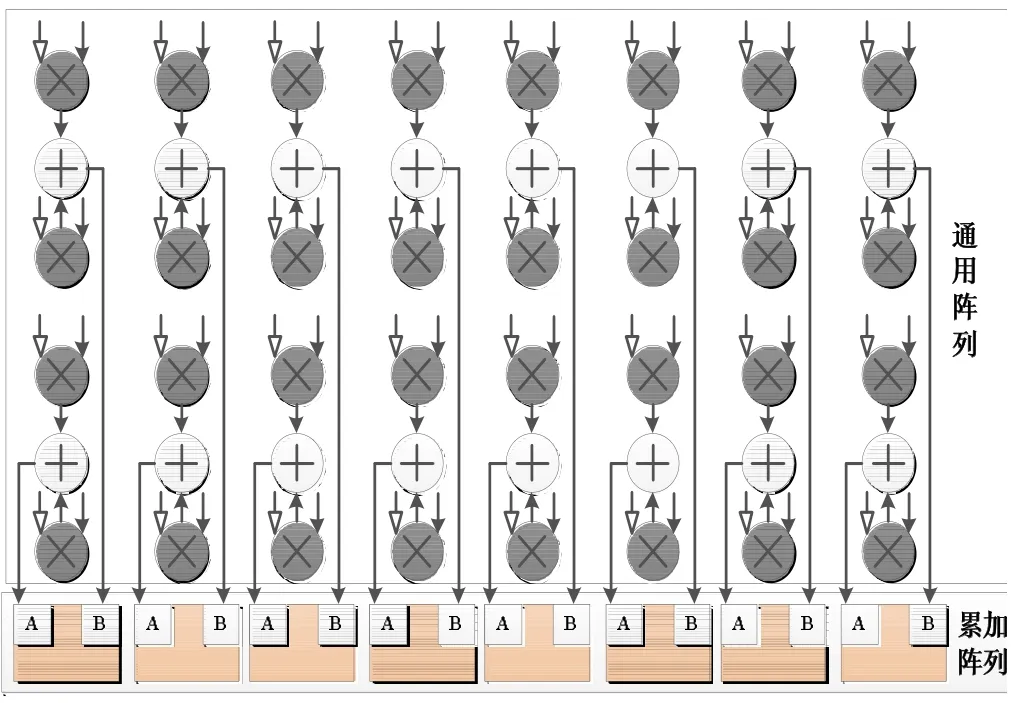
图8 三角矩阵相乘映射

3 实验结果及分析对比

本文基于RASP可重构架构的实现方法可适用于任意阶矩阵，具有高度的灵活性。对于高阶矩阵，当矩阵阶数为48时，操作域的利用率为50%，而在96阶矩阵消元中，利用率可达100%。所以，本文的方法在高阶矩阵应用时效果最好。本文将基于RASP可重构架构实现矩阵求逆方法的实验结果与其他不同的矩阵求逆方法包括DSP、FPGA等比较，实验结果表明，相比DSP，本文提出的矩阵求逆在3-9阶矩阵时，性能是DSP的几十倍，计算性能远高于DSP，同时本方法还可用于高阶矩阵。与FPGA相比，虽然低阶矩阵性能略低，但是对于高阶的36阶矩阵，性能提高了1.19倍，接近ASIC性能，相比于ASIC架构实现，本方法又同时兼顾了高性能和高灵活性的要求。矩阵求逆性能指标对比见表1。

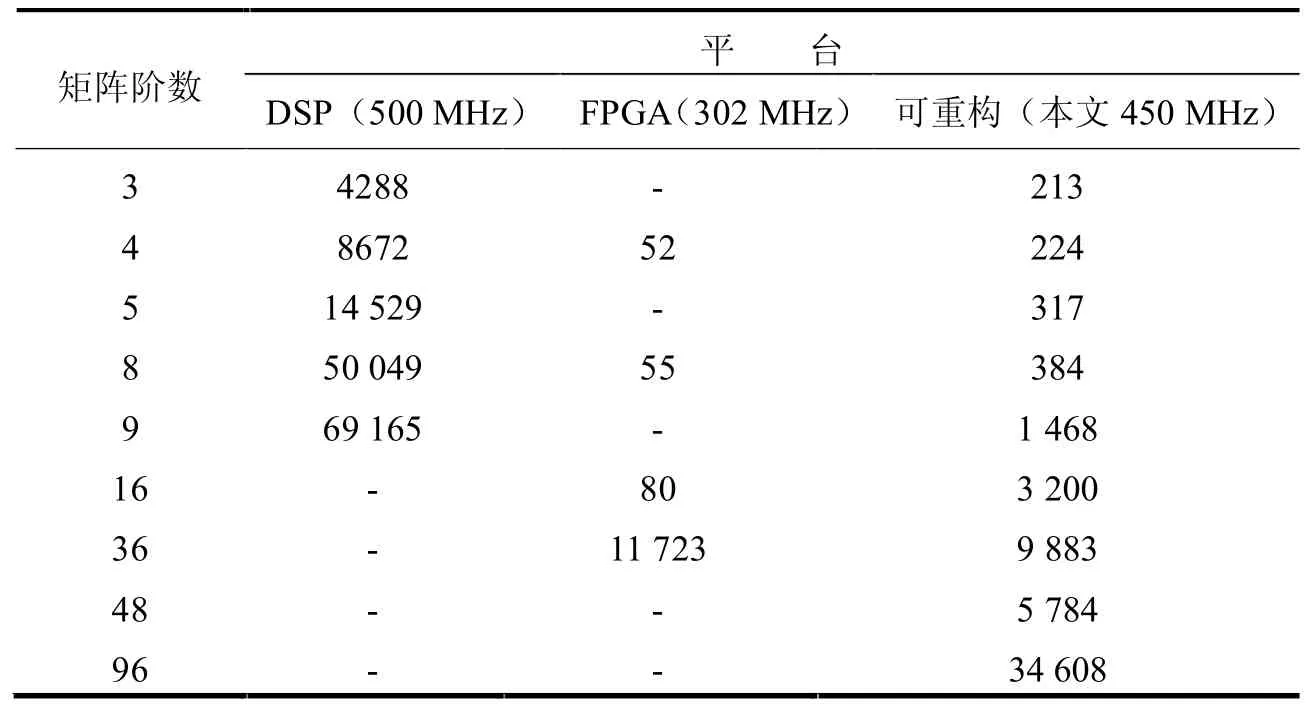
表1 矩阵求逆性能指标对比

4 结论

矩阵求逆是通信领域的核心算法之一，本文提出了一种基于动态可重构阵列的矩阵求逆算法实现方法，选取硬件并行度高的LU分解矩阵求逆算法，通过对该算法的数据流分析，详细设计了该算法在RASP架构上的映射方法，并进行性能分析。结果显示，本文的设计方案适用于任意阶矩阵，灵活性高。性能在低阶时优于DSP，且在高阶矩阵方面有较大优势，高阶性能相比FPGA提高了1.19倍，接近了ASIC的性能，并比ASIC灵活。因此本文提出的基于可重构阵列的矩阵求逆算法实现方法可同时兼顾性能和灵活性。