基于模糊滑模控制的无人车路径跟踪
2022-05-07王扬帆尹凯璇王子涵
李 哲,王扬帆,尹凯璇,王子涵,王 昊
(1.唐山市交通运输局,河北省唐山市路北区大里路125号 063000;2.北京科技大学自动化学院,北京市海淀区学院路30号 100083)
智能车辆作为人工智能时代的新兴产物,打破了传统的人车路交互方式,将驾驶员操作失误的概率降为零,提高了交通的安全系数,降低了能源消耗。因此对路径跟踪控制的研究具有很大的实用价值。
在智能车运动控制中,滑模变结构控制具有很好的抗干扰性,被广泛应用于车辆横向控制中。德国航天航空研究院的阿克曼基于阶梯控制的思想设计了滑模跟踪控制器[1],使得车辆横摆角速度误差收敛到零,仿真验证了该控制算法的有效性。贡比涅技术大学的Tangne等人[2]将高阶超螺旋滑模控制方法用于车辆控制,并使得横向位移误差收敛为零,降低了在较大道路曲率路况时的抖振现象,哈尔滨工业大学的王聪[3]建立了车辆的质心侧偏角模型以及轮胎非线性模型,使用模糊滑模控制算法设计了车辆的横向控制器。实验结果表明,所设计的控制器在两轮转动车辆和四轮转动车辆上均有良好的跟踪效果,为了增强无人车辆在极限工况下较大道路曲率路况时的转弯稳定性,吉林大学的王荣本等人[4]将滑模变结构控制运用于路径跟踪控制器当中,并基于最优控制理论设计了滑模切换函数。仿真表明,所设计的控制器在匀速时可以迅速减少车辆的横向偏差并保持车辆的稳定性。高秀晶等人[5]基于最优控制理论设计了滑模切换函数,仿真表明所设计控制器具有很强的鲁棒性。王家恩等人[6]改进了对位置偏差进行控制的传统思路,基于滑模控制提出了一种基于车辆横摆角控制的新方法,该控制方法使得被控车辆能够在实时规划当前点到预瞄点路径的同时完成路径跟踪任务,但是常规的滑模控制由于切换项增益恒定而存在抖振现象,使得车辆稳定性下降。因此,文中提出了一种基于模糊切换增益调节的控制算法来自适应调节滑模增益率以降低切换项所产生的抖振。
1 建立模型
1.1 车辆动力学模型建立
真实车辆的动力学特性极其复杂,如果不简化会极大地增加计算工作量,并且模型变复杂而带来的精度提高远比不上设计控制器所带来的复杂性提升[7]。因此二自由度模型优势显著,它既保持了对车辆关键参数如质心侧偏角等的建模,又能够大大降低模型的复杂性。故文中以智能车辆的前轮自动转向控制为目标建立车辆二自由度模型。文中所设计的智能车路径跟踪控制系统是基于电动助力转向系统来实现的,首先基于上层履带跟踪控制器计算得出理想的前轮转向角,再乘以传动比得到理想的方向盘转角,最后将该被控量发送至Carsim中车辆Steer模块以实现位姿控制。图1是二自由度动力学模型示意图。图中,Vx,Vy分别为车辆的纵向速度和横向速度;V是车辆的速度;λ为车辆的质心侧偏角;η为车辆的前轮转向角;n,m分别表示车辆前后轴到车辆质心的距离;q为车辆前后轴之间的距离。
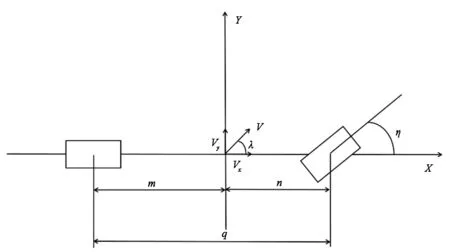
图1 车辆二自由度动力学模型Fig.1 Two-degree-of-freedom dynamic model
根据图1可以得到动力学方程为
(1)
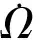
(2)
式中,D为系统建模的不确定性。
1.2 驾驶员模型建立
驾驶员模型是基于最优预瞄理论所推导建立的,借助该模型可以求得车辆的理想横摆角速度[8]。假设汽车在转向过程中横摆角速度是恒定的,故可以将汽车的行驶过程视为汽车绕着半径为R的圆弧做圆周运动,具体行驶轨迹参见图2。XOY是以无人车为中心所建立的坐标系,W点是车辆的质心位置,Q点为参考路径上与预瞄点横向相切的点,A为WQ的中点,C点是速度V的延长线与Q点沿X轴垂线的交点,B点是无人车行驶过程中的预瞄点,该点的选取与车速以及预瞄时间Tp1有关,车辆实际速度V与车辆坐标系X轴的夹角为车辆侧偏角λ,Δf是预瞄点的横向偏差。基于汽车横摆角速度基于恒定的假设,汽车将在Tp1秒后从W点行驶到Q点,并且路径WQ是以E为中心、R为半径的圆弧。
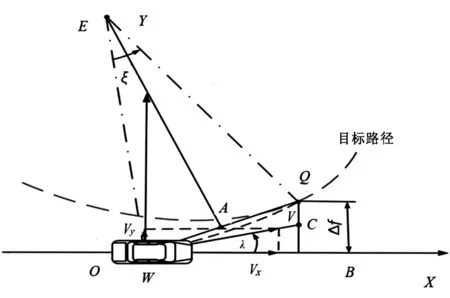
图2 稳态圆周运动下汽车行驶轨迹Fig.2 Car trajectory under steady circular motion
由图2可以得到理想的车辆横摆角速度Ωd为
(3)
式中,ξ为该段圆弧的圆周角,根据三角形的边角关系可进一步推得:
(4)
2 控制器设计
常规滑模控制存在抖振问题,为消除这种抖振需要依据经验自适应地调节滑模增益率,由于模糊控制是一种规则驱动的不需要精确模型的控制方法,相较其他控制方法而言,能够方便有效地使用模糊规则表达领域专家的主观经验,故文中提出采用模糊控制策略来调节滑模增益率。
分别设计滑模面和滑模趋近律如下:

(5)
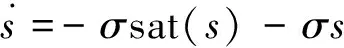
(6)

(7)
式中,Ωr为车辆实际横摆角速度,E*(t)为参数摄动和未知干扰项,l11,k11,k12,g(Ωr)如式(8)所示。
g(Ωr)=k11Ωr+k12λ
(8)
滑模控制中抖振运动的剧烈程度决定着到滑模运动质量好坏程度,因此一方面需要较大的滑模增益使状态空间中的点迅速到达滑模面,另一方面还要削减滑模增益从而削减抖振运动[9]。为此,文中设计了模糊滑模控制器以自适应调节增益。滑动模态的广义存在性条件为
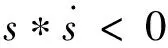
(9)
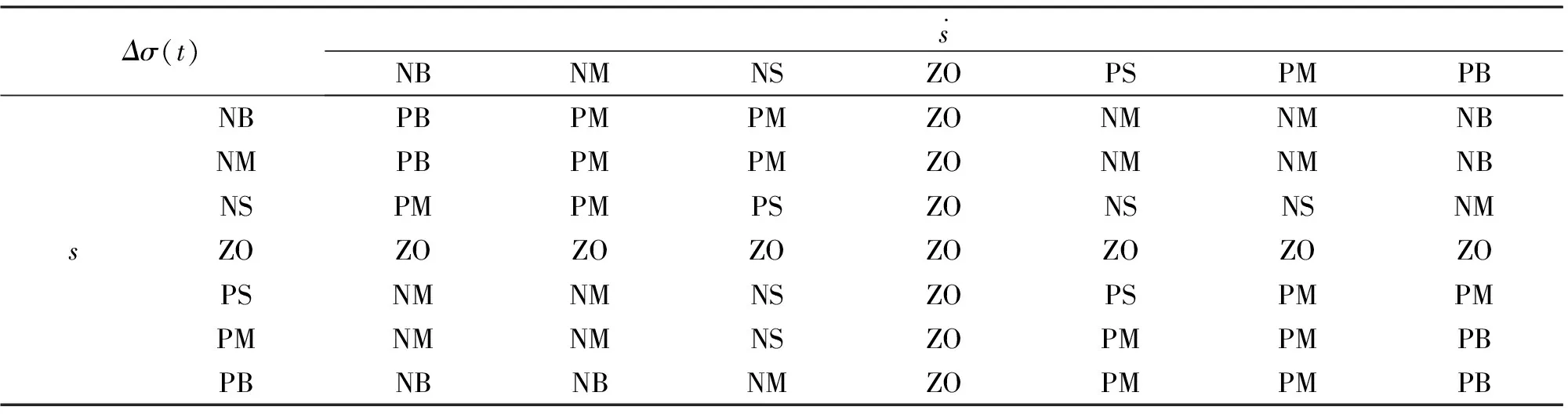
表1 模糊规则
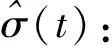
(10)
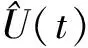
(11)
3 实验及结果分析
基于Carsim/Simulink搭建无人车路径跟踪联合仿真平台,选取车辆为F-Class Sedan。在Carsim中,设置道路附着系数为0.2、车速为15m/s、仿真时间T为35秒,分别测试横向跟踪偏差e1、车辆输出的质心侧偏角λ、横向加速度ay、方向盘转角δsw、车辆实际路径横向坐标Y并与参考路径横向坐标Yd作对比。
3.1 跟踪性能测试
车辆跟踪效果如图3(a)所示,其中红色轨迹为Yd,绿色轨迹为Y,横向距离跟踪偏差e1如图3(b)所示,车辆质心侧偏角λ变化如图3(c)所示,车辆加速度ay变化如图3(d)所示,方向盘转角的输出δsw如图3(e)所示。
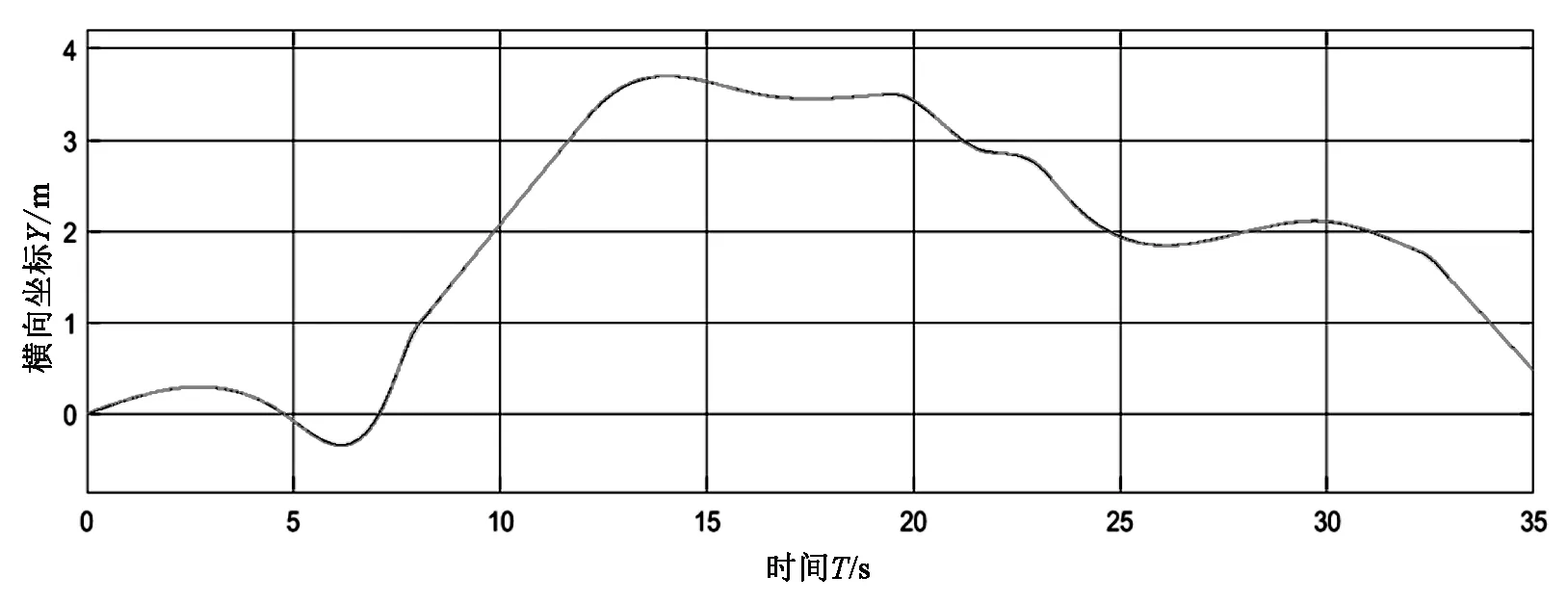
(a)横向位置对比
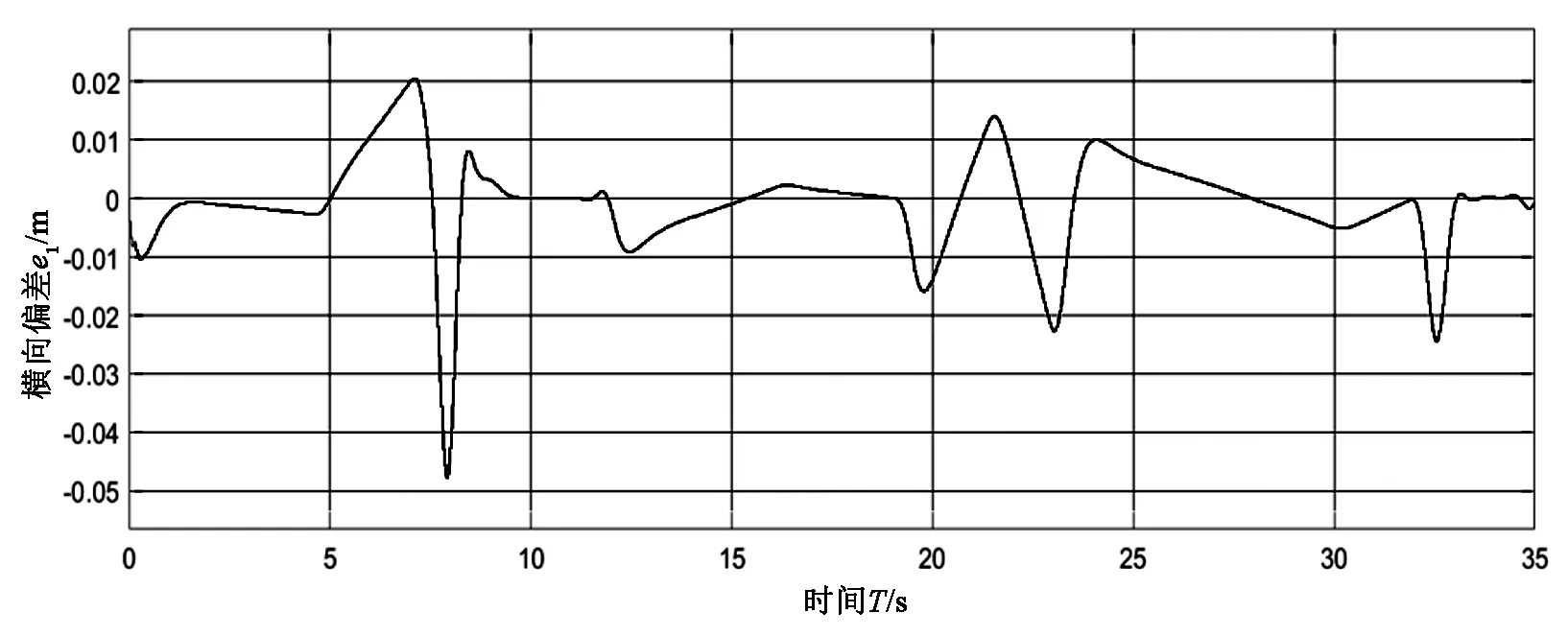
(b)横向距离跟踪偏差
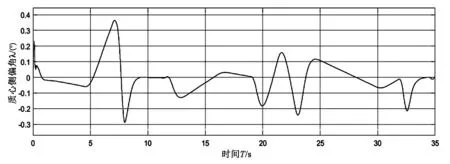
(c)质心侧偏角
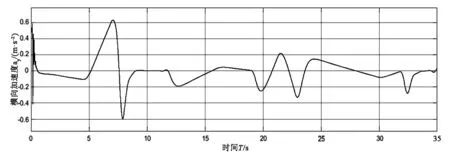
(d)加速度变化
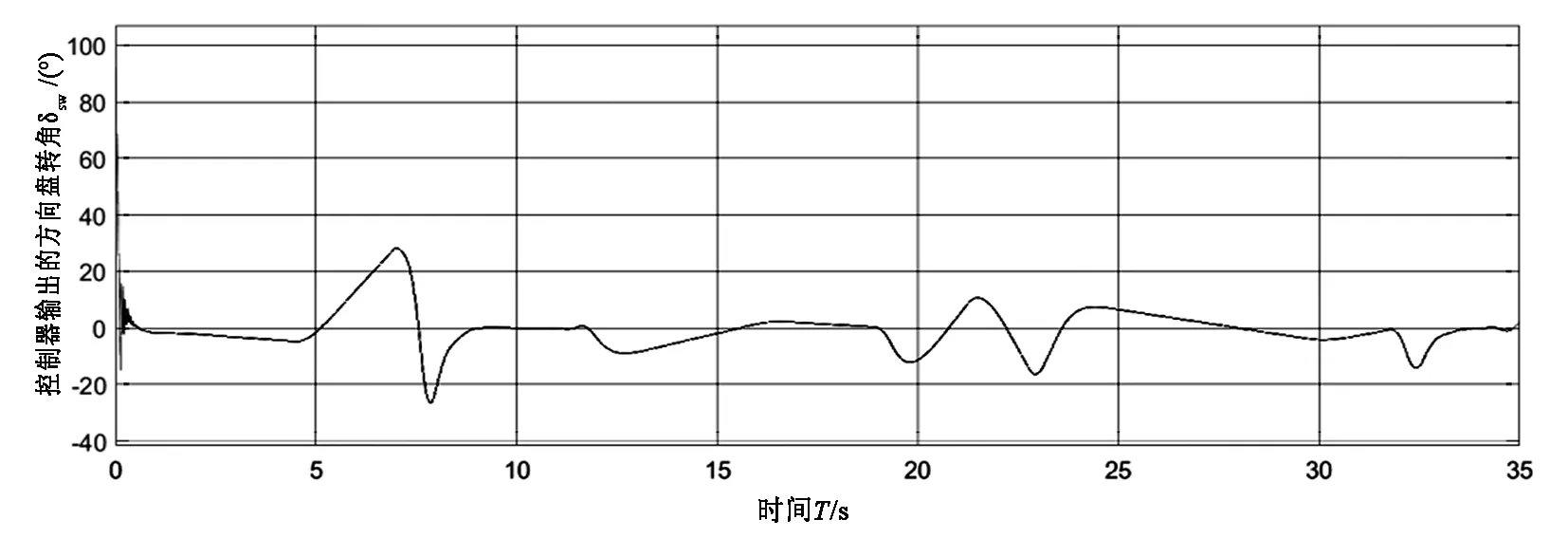
(e)方向盘转角图3 基于FSMC的车辆跟踪性能Fig.3 FSMC-based vehicle tracking performance
由图3(a)可以看出车辆参考路径与实际路径贴合很紧,跟踪效果较好,由图3(b)、(c)、(d)可知横向距离跟踪偏差的波动范围是-5cm~3cm,质心侧偏角的波动范围是-0.3°~0.4°、加速度的波动范围是-0.6m/s2~0.6m/s2。由图3(e)可以看出方向盘在公式(11)两个模型切换中调节幅度也较小,说明该控制器能有效消除抖振。
3.2 鲁棒性测试
本节在车辆跟踪的开始阶段给横向速度和车辆横摆角速度两个参数均加入强度为1的白噪声。车辆路径对比如图4(a),其中红色轨迹为Yd,绿色轨迹为Y,横向距离跟踪偏差如图4(b),车辆质心侧偏角、加速度、方向盘转角变化分别如图4(c)、(d)、(e)所示。
由图4(a)知车辆参考路径与实际路径贴合较好,跟踪性能强。由图4(b)(c)(d)知车辆横向跟踪偏的差变化范围是-8cm~10cm、质心侧偏角与加速度的变化幅度也较小,分别为-0.2°~0.3°、-0.6m/s2~0.6m/s2,由图4(e)知方向盘转角变化幅度较小,表明所设计的模糊滑模控制器鲁棒性强。
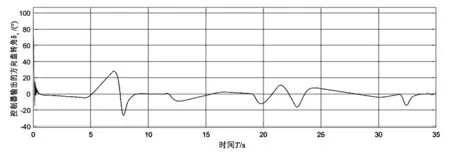
(a)横向位置
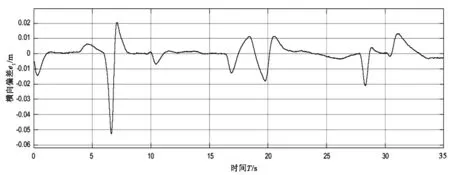
(b)横向距离跟踪偏差
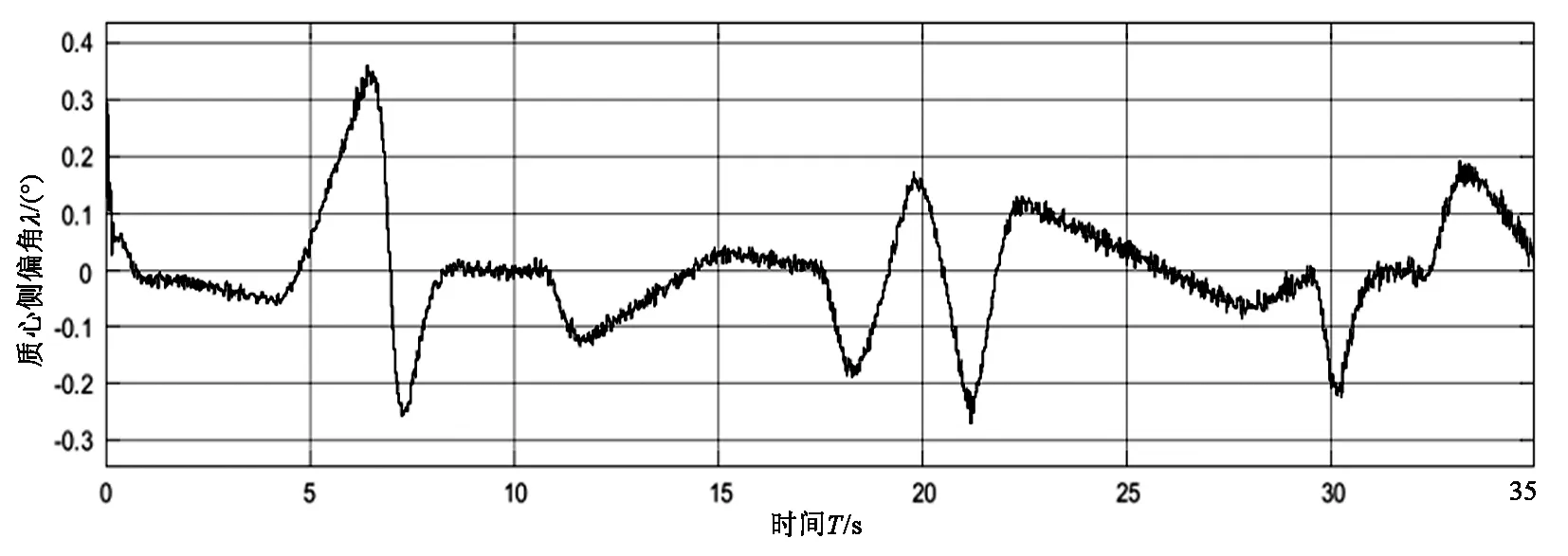
(c)质心侧偏角
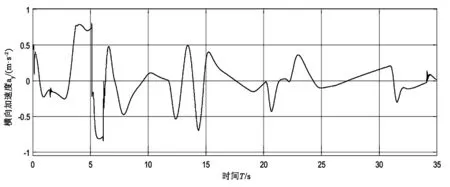
(d)加速度变化
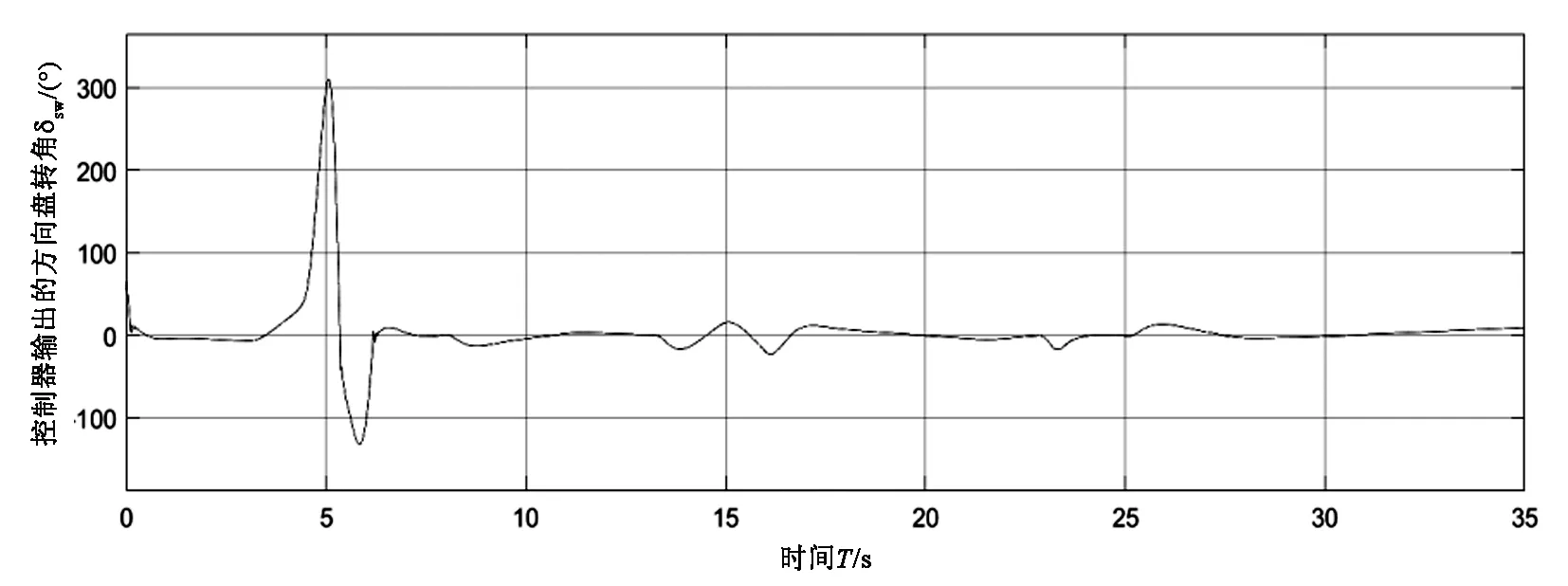
(e)方向盘转角图4 基于FSMC的车辆鲁棒性能Fig.4 FSMC-based vehicle robustness
4 结论
针对无人驾驶汽车的路径跟踪技术,本文开展了以下工作:
(1)在忽略空气动力学和车辆悬架动力学的情况下建立了二自由度车辆动力学模型,对车辆的横摆角速度动力学方程进行了推导。建立了驾驶员模型,求解出理想横摆角速度,为后续控制器设计打下基础;
(2)基于Simulink/Carsim平台进行跟踪性能与鲁棒性能测试,仿真结果表明采用模糊滑模控制器时车辆不仅能够完成高精度的路径跟踪任务,而且具有较强的抗干扰能力。
