运用Geogeb ra软件模拟水中月亮像的大小和位置*

吴彬彬

（苏州市相城区春申中学 江苏 苏州 215101）

在初中物理教学中，教科书及其相关的教辅资料均将平静的水面视为平面镜.由平面镜成像特点“像与物大小相等、像与物到镜面的距离相等”可知，在平静的水面上方飞翔的小鸟，它的像和它本身大小相等，离水面的距离也相等.这一点毋庸置疑，因为在我们生活范围内物体的线度比较小，水面看起来真的是“平”的.

同理，也有大量针对水中月亮和天上月亮大小比较的试题出现.那么水中月亮和天上月亮真的一样大还是看起来一样大？

为了方便研究，我们运用Geogeb ra软件通过作图进行分析.

1 月亮半径、地球半径和月地距离的大小关系

通过查阅资料，已知月亮半径r=1 737 km，地球半径R=6 400 km，月地距离S=384 000 km.为了方便作图，我们将月亮半径作为1，而地球半径近似为4，月地距离近似为240.如果将地球上的水面比作一个曲率半径为4 m的广角镜，那么月亮便是240 m外的物体，此时水面的弯曲程度相当可观，不能作为平面镜看待，而应该作为凸面镜.那么月亮通过地球水面上成像应该是一个缩小的像.

2 用Geogeb ra软件作出月亮通过地球水面成的像

2.1 用两条特殊光线作出月亮的像

首先在坐标（0，0）位置画出一个半径为1的月亮，在坐标（6，0）位置画一个半径为4的地球，过A点作两条光线（一条为指向地球球心，这样可以原路返回，另一条平行于月心和地心连线），两条反射光线的反向延长线交于A′点，则相应的月球圆心A1的像在A′1的位置，如图1所示.我们用月亮的半径和它的像的比较来表示月亮和其像的大小关系.

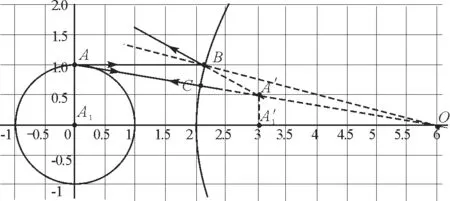
图1 地很近时，月亮半径的像A′A′1

从图上可以看出月亮的像比月亮小，像到地面的距离比月亮到地面的距离小.当然，此时的地球并不在其真实的位置上，我们需要将地球向右移到距离月亮240的刻度上.

保持月亮的位置不变，将地球移到（240，0）的位置上，此时月亮的像已经小得看不见了，如图2所示.

放大图像得到如图3所示的像A′A′1，使用软件进行数据分析，A′的坐标为（237.919，0.008 68），即当月亮的半径大小为1时，像A′A′1的大小为0.008 68，像到地球表面的距离为S′=237.919-236=1.919，显然像比月亮小得多，像到水面的距离比月亮到水面的距离也小得多.

图3 放大后月亮半径的像A′A′1

当然，我们知道此时的像是在BC范围内观察到的，这个范围实在是太大，我们的眼睛没有这么大，所以此时得到的像不是我们人类实际观察到的大小和位置，没有参考价值和意义.

2.2 模拟出人眼能够观察到的像的情况

由于人眼的瞳距在7 cm左右，而月亮的直径在3.5×106m，即人眼瞳距是月亮直径的2×10-8倍.如图4所示，将作图环境放大到原来的108倍，这样我们可以选择两条非常接近的入射光线，这样它们经过地球水面的反射后可以同时进入人眼（B和C两点为实际上相距为1 cm左右的两个入射点，且B点在月心和地心的连线上），此时两条反射光线的反向延长线的交点就是人实际观察到的像.如图5所示，此时A′的坐标为（237.983 16，0.008 4），即像的大小为0.008 4，可得像到地球表面的距离为S′=237.983 16-236=1.983 16.此时的像相对于前一次更小了，这也足以说明水中的月亮比天上月亮不但小而且小得多.

图4 两个入射点距离接近瞳孔距离

图5 A′的坐标

3 为什么水中月亮和天上月亮看起来一样大

“又疑瑶台镜，呼作白玉盘”.月亮实际很大，但是我们总觉得它只有盘子这么大，究其原因是它离我们实在太远，所以看起来比较小.我们判断物体的大小取决于物体发出或者反射的光线进入眼睛的夹角大小，此夹角称作视角，视角越大，物体看起来就越大.

如图6所示，人在B点看月亮时的视角为2α，已知A1点坐标为（0，0），B点坐标为（236，0），则tanα==0.004 237.如图7所示，人在B点看水中月亮时的视角为2β，已知A′的坐标为（237.983 16，0.008 4），则tanβ==0.004 236，可以发现虽然水中月亮比天上月亮小得多，但是我们观察它们的视角几乎相同，这就是水中的月亮和天上的月亮看起来一样大的原因了.

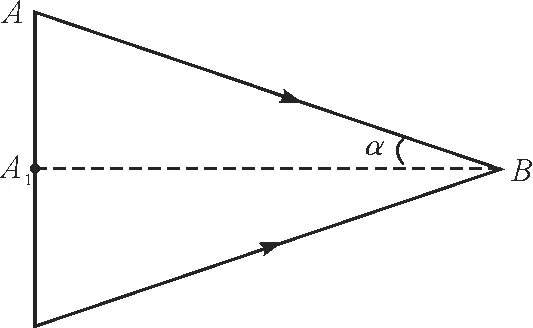
图6 人在B点看天上的月亮

图7 人在B点看水中的月亮

4 结束语

在教学的过程中有些现象由于某种巧合，用一定的知识、原理也能解释得通，但是并不符合物理原理.如本文中水中的月亮和天上的月亮看起来一样大，所以就联想到了平面镜成像原理.通过Geogeb ra软件的模拟可知，水中的像相对于天上的月亮小得多，只是离我们近而已.物理教学应该抓住事物的本质，而不能将现象和原理硬凑在一起，以致贻笑大方.