小议流体情境中的相互作用和功率问题

2022-05-07段宝维张燕怡

物理通报 2022年4期

段宝维张燕怡

（中国人民大学附属中学北京 100080）

1 背景介绍

2020年《普通高中物理课程标准》特别重视问题“情境”，一共有67处提到“情境”问题，强调问题、任务、试题情境，并把学生将“情境与知识相联系的水平”作为学业质量检测的高阶要求，具体又细化为：将情境中的经历转化为物理探究过程、将情境中的故事情节转化为物理现象、将描述情境的文字转化为物理表述、将情境中需要完成的工作转化为相应物理问题［1］.

我们常说某个问题出得很“活”，其“活”的本质之一在于情境的转化，能否把问题中的实际情境转化成解决问题的物理情境，建立相应的物理模型，这是应用物理观念思考问题、应用物理知识分析解决问题的关键.在物理教学中，应让学生获得在实际情境中解决物理问题的大量经验，形成把情境与知识相关联的意识.

流体问题，如高压水枪冲击、喷泉托举物体、气体压强微观解释、离子发动机反冲、自动称米机的争议……取材于生活实际，现象常见而富有一定趣味性，是将情境与物理模型结合，培养学生应用力学工具解决具体问题的良好素材［2～5］，属于综合性强、难度较大、对能力要求较高的题目，多见于高考和各类高三模拟测试中.

流体情境的常见问题分为两类：（1）讨论流体与环境的相互作用，常规方法是微元思想配合动量定理求解；（2）讨论流体喷射的功率，常规方法是应用能量转化关系.学生在具体思考的过程中常有质疑，为何对于同一问题，不同方法讨论的结果经常不自洽：如用能量观点求流体作用力，或基于相互作用和功的定义计算流体功率，往往与正确答案不符.究其原因，在于没能建立合适的理想化模型，对物理规律的适用条件、研究对象范围把握得不够清晰准确.

本文试图回顾流体情境中的经典问题，从概念、规律的深入理解角度，厘清学生们的常见误区，并基于中学物理的常见模型，做一些拓展讨论.

2 问题回顾

如下是流体情境中涉及相互作用的经典例题.

【例1】水流射向墙壁，会对墙壁产生冲击力.假设水枪喷水口的横截面积为S，喷出水流的流速为v，水流垂直射向竖直墙壁后速度变为零.已知水的密度为ρ，重力加速度大小为g，求墙壁受到的平均冲击力F.

此题的传统解法如下：

取Δt时间内入射到墙面上的一小段水柱为研究对象，水柱质量Δm=ρSvΔt，受到墙壁反作用力F′，动量由Δmv变为零，设水柱入射方向为正方向，由动量定理

解得

但如果用动能定理求解，认为墙壁对水做功

于是由动能定理

就会得到错误的结果

以下是流体情境中涉及功率的经典例题.

【例2】（人教社2019版《物理·必修2》教材P94练习6）：图1是某城市广场喷泉喷出水柱的场景.从远处看，喷泉喷出的水柱超过了40层楼的高度；靠近看，喷管的直径约为10 cm.请你据此估计用于给喷管喷水的电动机的输出功率至少有多大？

图1 城市广场喷泉场景

根据功能关系，喷泉喷水功率应等于水在单位时间内获得的动能，通过喷水高度估算水流出口时的速度v，通过喷管直径d和出口速度v估算单位时间喷出的水量，有

代入实际数据，不难求得数值解.

但是，按照例1动量定理求解的正确思路，同样可以求得，出口处喷管对水流作用力为

则有功率

3 误区分析

在例题1所代表的流体（我们先局限于不可压缩的理想流体）冲击问题中，动能定理并不是适合的物理规律，原因如下：

（1）中学物理中的动能定理，实际上是单个质点的动能定理，而题目中的研究对象——“一小段”水柱，即使再短，也不可以看作质点，因为它必须流动、必须形变，应看作质点组，内力做功引起的动能变化不可无视；

（2）若将水柱看作质点组，严格意义上说，墙壁外力的作用点并没有移动，因此，对水柱并没有做功，自然也不能利用W=-F（vΔt）的公式.否则，根据“功是能量转化或转移的量度”，墙壁的能量应有所减少，与实际情况矛盾（类似2006年高考题“人从地面起跳、地面对人不做功”的情境）；

（3）如果改变题目条件，让水柱原速反弹或水流以相等速率沿墙壁散开，则水柱动能不变，自然也无法运用动能定理，但用动量定理依然可以得到正确的结果.

在例题2的情境中，题目强调求“最小功率”，也就是没有损耗或浪费的情况，此时，认为喷泉做功全部转化为喷出水的能量，无疑是正确的.而如果用功率公式P=Fv求解，则需明确，该公式描述的，依然是某个外力F对某个速度为v的质点的做功快慢情况.参考例题1的解法，若此处代入F=ρSv2，则F应该是“如果在喷口垂直水流方向放置一个挡板，并且水流冲击挡板后不反溅，只是顺着挡板平面流走时，水流对挡板的冲击力”，而并非是“将喷口处一小截水柱看作质点，该水柱从零加速到出射速度v受到的力”.

利用如图2所示的理想装置，可以从“力×速度”角度解释例题2所要求的最小功率.以不可压缩理想流体定常流动时的一组流管为轮廓，构造如图2所示的刚性容器，则在很短时间内，忽略一切摩擦损耗，活塞端所受压力F所做功，将几乎全部转化为喷出液体的动能.此时喷射器功率满足

图2 不可压缩流体定常流动示意图

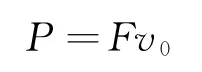
但显然，此时F为活塞处受力，并非喷口处的冲击力ρSv2，而速度部分也应代入活塞被推进的速度v0，而非喷口处水的出射速度v.

参考伯努利原理的证明过程，在活塞处压力做功=水获得的动能增量，在极短时间Δt内，有

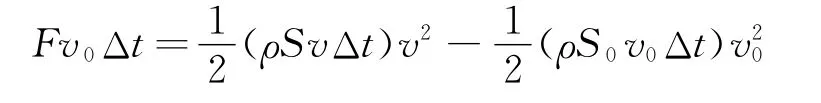
根据连续性原理

与能量角度的计算结果一致.

4 对流体作用力的拓展讨论

为了彻底厘清动能定理不能简单应用于流体作用力求解的疑惑，我们再看下面例题.

【例3】（由2018年北京市昌平区高三期末统测改编）离子发动机是利用电能加速工质（工作介质）形成高速射流而产生推力的航天器发动机.其原理如图3所示：首先电子枪发射出的高速电子将中性推进剂离子化（即电离出正离子），正离子被正、负极栅板间的电场（可视为匀强电场）加速后从喷口喷出，从而使飞船获得推进或姿态调整的反冲动力.这种发动机寿命长，适用于航天器的姿态控制、位置保持等.已知从喷口喷出的正离子速度大小为v，发动机功率为P，求该发动机产生的平均推力大小F.

图3 离子发动机原理示意图

解析：我们先用传统的动量定理方法求解.设在任意极短时间Δt内，喷出的离子总质量为Δm，这些离子获得的动量为Δmv，因此有

另一方面，考虑到飞船质量远大于离子质量，发动机输出的能量几乎全部转化为离子的动能，因此有

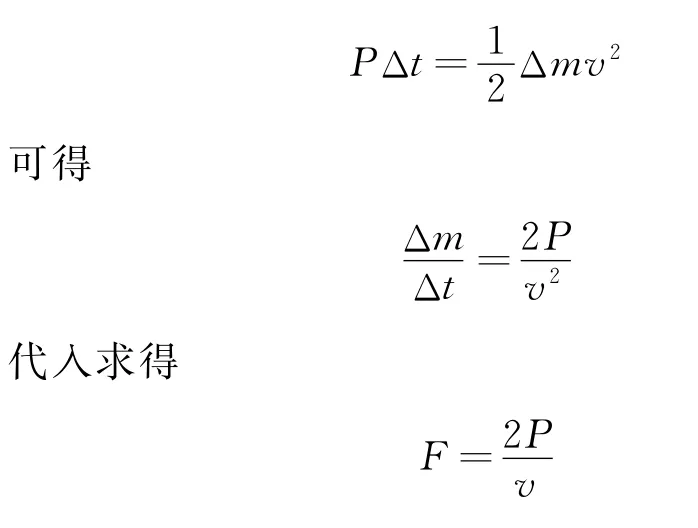
此处为何不能直接运用公式P=Fv得到F=我们再从微观粒子受力的角度来深入分析一下.

将离子在电场中的加速过程简化为如图4的模型，可以看到，由正负极板（负极为金属网且忽略打在金属网上的离子）、绝缘容器代表飞船发动机，其所受推力F的大小等于所有离子在电场中受力的矢量和F′（牛顿第三定律），而不仅仅是刚好离开容器的那些离子的受力.

图4 离子发动机简化模型

从能量关系入手考查，离子发动机总功率，可以看做是加速电场对每个离子电场力的功率之和，设第i个离子受力为Fi，某时刻速度为vi，则有

正、负栅极间电场被简化为匀强电场，显然，每个离子都受到等大的电场力

其中，N为某时刻电场中离子的总个数，v-i为N个离子瞬时速度的平均值.由于每个离子从正栅极到负栅极的受力-运动过程相同，v-i可以看作一个离子运动全过程的平均速度，离子都做匀加速直线运动，于是有

此时可发现，发动机推力大小与功率关系为

每一个Δt内，虽然电场中各个离子都得到加速，但等效看来，都相当于有一个薄层的质量为Δm、总电荷量为q的离子穿越电场，发生了位移L（L为两极板间距离），电场力对它做功

同理，图2中流管容器中的一小块液体，也可认为是穿越了整个流速场，直接到达喷口，从而将外力F做的功转化成了自身动能.

5 对流体喷射功率的拓展讨论

前面关于例2的分析，我们默认流体的喷射功率，严格等于流体单位时间增加的动能，即喷射器转化效率是100%，但实际情景未必如此.在实际喷水过程中，考虑到粘滞阻力、流体与管壁摩擦等因素，喷射器的功率，应等于将水从静止加速度到喷射速度v所做的总功.

我们以“传送带”传输矿粉的例子作为类比进行说明.

【例4】如图5所示，水平传送带以速率v=2 m／s的速率匀速运行，上方料斗每秒将40 kg的矿粉竖直放落到传送带上，然后一起随传送带匀速运动，如果要使传送带保持原来的速率匀速运行，则皮带机应增加的功率为多少？

图5 传送带运送矿粉示意图

解析：设Δt时间内有质量为Δm的矿粉被投放到传送带上，对于传送带上的矿粉整体，Δt时间内总动量增加了Δmv（注意，矿粉从静止加速至与传送带共速的时间不一定是Δt）.

处于加速状态的矿粉受摩擦力f，根据动量定理fΔt=Δmv，传送带受矿粉反作用力

结合前面分析可知，这个f′是所有矿粉对传送带的摩擦力.

传送带保持匀速v运动，电动机需额外克服f′提供能量，因此需额外增加的功率P，等于电动机对传送带增加的拉力，再乘以传送带速度

另一方面，矿粉在单位时间内获得的动能仅仅为

根本原因在于，矿粉加速过程中与传送带有相对滑动，存在摩擦生热引起的损耗（参考2003年高考全国压轴题）.不难得到本情境中，如果矿粉离开传送带时已经与传送带共速，发热功率和发动机为矿粉提供动能的功率相等，各为.而如果传送带速度很大，以至于矿粉离开传送带时无法加速到v，摩擦生热损耗的能量将大于矿粉得到的动能.

对于喷射器喷水求功率的问题，如果我们只考虑水增加的动能，则可以按照发动机模型处理，得