生猪运输车烘干房气流组织模拟及优化

郝文彬， 冯天玉， 朱望武， 黄世明， 程 捷

(1 湖北工业大学农机工程设计研究院， 湖北 武汉 430068； 2 武汉市红之星智农机械有限公司， 湖北 武汉 430000)

生猪转运车的烘干房在防疫环节占据着重要的位置。转运车在进行运输工作前必须进行清洗、消毒、烘干等一系列流程，其主要目的是消灭转运车上的病毒，切断病毒传播途径[1]。 本文研究的对象是畜禽洗消中心的烘干房，研究其内部存在的气流组织流速较低和温度场分布场不均匀的问题。若现场进行调整优化，必将耗费大量的人力、物资，且时间周期长，做的无用功较多。所以采用CFD软件进行仿真测试，首先验证数值模拟的准确性，再进行结构优化，得出更为合理的烘干房结构，形成较好的气流组织和温度场。

1 仿真模拟及验证

1.1 物理模型

初始烘干房由燃烧系统、热风循环系统、烘干房房体和温度控制系统等4个部分组成，烘干房采用侧面送风、侧上部回风的方式进行热风循环。图1是烘干房的物理模型，表1是烘干房模型参数。

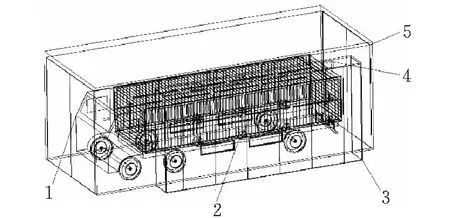
1-汽车车身;2-送风口;3-耳房;4-回风口;5-烘干房房体图 1 烘干房模型

表1 烘干房模型的参数

1.2 控制方程

烘干房内的气流流动要遵守物理守恒定律[2]。控制方程是这些守恒定律的数学描述。

1)质量守恒方程(连续性方程)

质量守恒方程的形式为[3]:

(1)

式中：p为流体密度，kg/m3；t为时间，s；u、v、w为速度矢量在x、y、z方向上的分量。

2)动量守恒方程(运动方程)

该定律可以导出x、y和z方向的动量守恒方程:

(2)

(3)

(4)

式中：P是流体微元体的压力；τxx、τxy和τxz是分子粘性作用产生的粘性应力τ的分量；Fx、Fy和Fz是微元的体力，如果体力只含重力，而且Z轴竖直向上，则Fx=0，Fy=0,Fz=-pg。此公式适用于任何流体均成立的动量守恒方程。

3)能量守恒方程

能量守恒方程：

(5)

式中：T为温度，K；k为流体的传热系数，W/(m2·K);cp为定压比热容，J/(kg·K);ST为粘性耗散项。

1.3 网格划分

采用ICEM软件对烘干房的物理模型进行网格划分。烘干房模型比较复杂，对四面体复杂模型进行高效快速的网格划分，同时对送分口和回风口进行局部加密处理。图2为烘干房各坐标轴网格划分示意图。

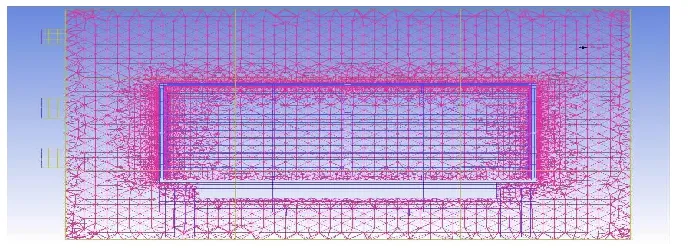
(a)X轴方向

(b)Y轴方向

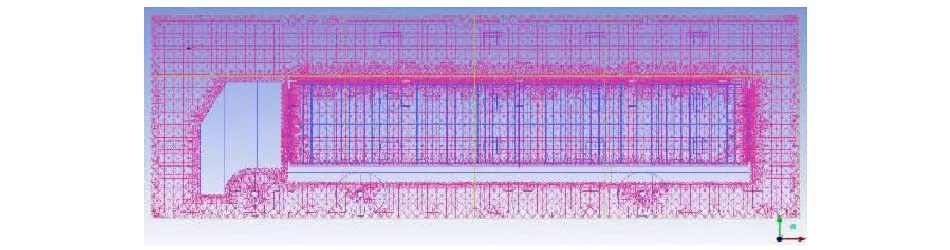
(c)Z轴方向图 2 网格划分

1.4 数值方法

烘干房的气流组织属于高Re数紊流流动且比较复杂，综合考虑计算准确性和计算机的性能，最终选用标准κ-ε模型，采用有限体积法FVM为离散方法[4]，离散后选用分步法迭代求解[5]。根据烘干房的参数设置边界条件，选择离散辐射模型，求解器选用的是FLUENT5/6。

1.5 实验验证

现场试验选取烘干房中心点位置为温度测量点，速度测量点选择在车身的侧表面每间隔1 m的6个点进行监测,每20 s记录温度和数据，最终测得380 s的数据；速度点监测也是每20 s进行记录，每个点在同一时间点平均值为该条线上在该时间点的数值。图3是数值模拟与实验数据对比。

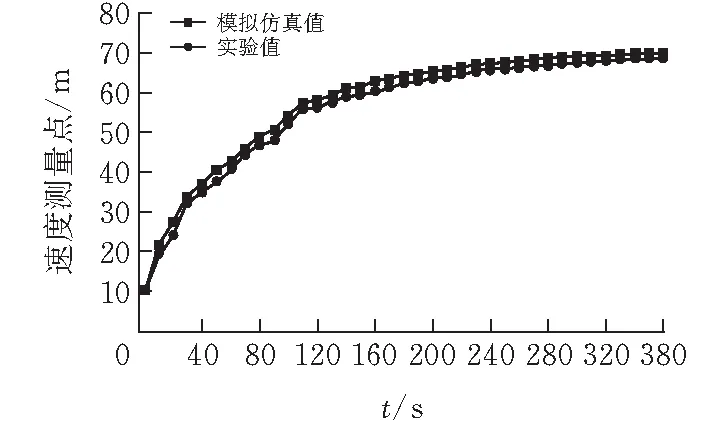
图 3 数值模拟与实验数据对比

2 烘干房气流组织优化

原始烘干房的气流组织速度为0.5 m/s，整个烘干房的的气流场速度较低，这不仅影响气体热量的交换速率，而且造成烘干房升温时间比较长且能耗增多。影响烘干效果的房内气流组织因素主要在于送风口及回风口的数量和位置[6]。故在现有烘干房基础上增加2个送风口，每排增加1个。另外，根据送风机的口面积等于回风口的面积，回风口的尺寸改为0.3 m×0.4 m的8个回风口。改进后的烘干房物理模型如图4所示

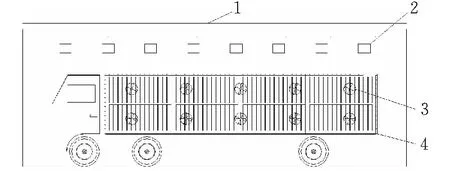
1-烘干房房体； 2-回风口； 3-送风口； 4-汽车车身图 4 优化烘干房模型

再进行模拟计算，得出的结果如图5所示。

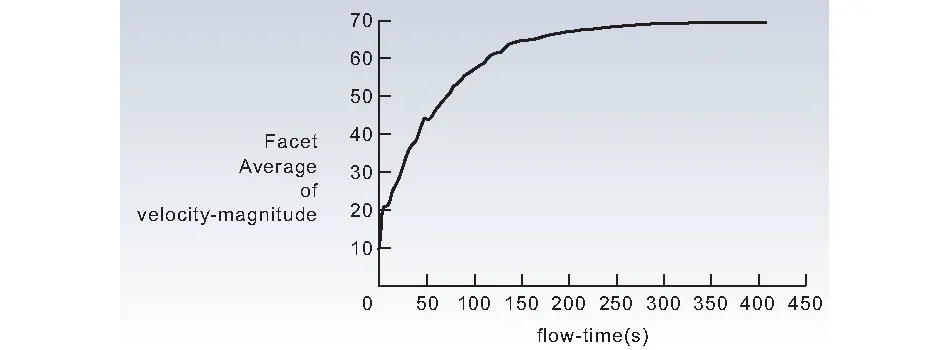
(a)温度随时间变化曲线

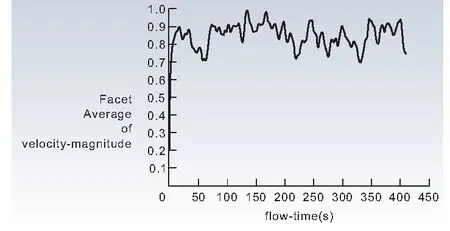
(b)z=2.78,y=0.6线上速度图 5 优化后烘干房的变化曲线

从图5模拟结果来看，在不改变初速度情况下，结构优化后整条线速度大约在0.9 m/s，相对于原始烘干房的0.5 m/s有一定的提高。与原始的烘干房相比较，升温的时间比原有的380 s,缩短了50 s。优化后烘干房能够快速达到目标温度，大大增加了工作效率。

3 工艺参数优化

3.1 正交实验设计

本次优化的目标是一次性开机使温度升到设定温度所消耗成本。以结构优化后的烘干房为对象进行模拟分析，将入口初速度和入口温度、环境的初始温度作为优化参数。

通过上述分析，选择3个因素(入口的初速度、入口的温度以及环境的初始温度)，对于每1个因素选取3个水平，采用L9(33)正交试验表格[7-8]。因素与水平的取值见表2

表2 因素水平表的设置

3.2 能耗的分析

烘干房在不断进行加热的过程，输送到房体内部的热量使得气温升高，当达到设定目标温度时，就不会再进行加热。在气体温度升高的过程中，有一部分热量被烘干房内壁吸收和外壁散失，所以在进行计算烘干房总的能量消耗时，不仅要考虑烘干房内部气体温度升高至设定值所消耗能，还应考虑内壁吸收和散失的热量。故总的消耗热量

Q=Q1+Q2+Q3

(6)

式中：Q为总消耗量;Q1为内壁面升温的消耗量；Q2为外壁面散失量；Q3为房内温度到设定值消耗的量。

1)内壁面升温的消耗量

Q1=M1+C1(Tt-T0)

(7)

式中：M1为壁面材料质量，kg；c1为材料比热容，kJ/(kg·K)；Tt为加热至稳定状态的温度，K；T0为初始温度，K。

2)外壁面散失量

Q2=AK(Tt-Tw)t

(8)

式中：A为外壁的表面积，m2；K为换热系数，kJ/(m2·h·K)；Tw为升温过程外壁的平均温度，K；t为一次升温到设定温度所需时间，h。

3)房内温度到设定值消耗的量Q3

烘干房从初始的温度，不断吸收热量直至到达设定温度，这段时间所吸收的热量就是烘干房空间消耗的量。

Q3=CVρ(Tt-T0)

(9)

式中：C为空气的比热容，J/(kg·K)；V为空气体积，m3；ρ为空气的密度，1.29 kg/m3

4)提供升温时间段提供的热量需要消耗的燃油量

(10)

式中：Lg为燃烧消耗量，kg；Q为烘干房升温消耗量，kJ；q1为液化石油气的热值，47000 kJ/kg；

5)送风机消耗成本

送风机主要输送热风，其机械转动靠电来维持，所以其消耗的成本是烘干房一次从初始温度升高到设定温度的时间内的电能。风机的功率

(11)

式中：Pw为风机功率，kW；Q为送风量，m3/h；P为风机全压，Pa；n0为内效率；n1为机械效率。

消耗的电量

P=Pw·t

(12)

通过分析燃烧的液化石油气的量和耗电量，以此计算烘干房的升温成本。在市场液化石油气和工业用电的价格基本保持不变的条件下，计算出不同参数下所消耗的成本，通过对比分析得出最优工艺参数方案(表3)。

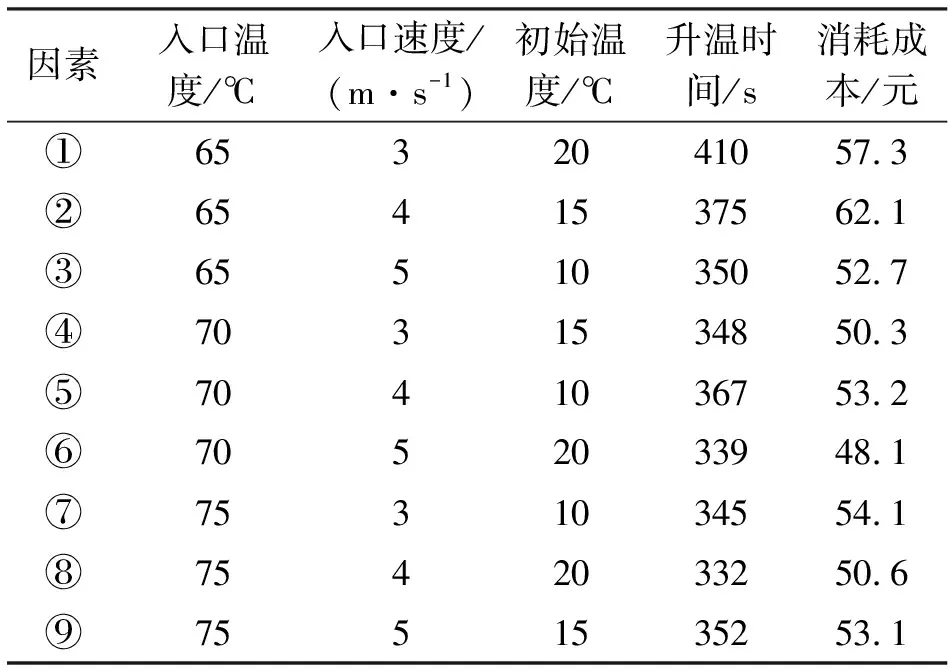
表3 烘干房能耗成本分析

从正交试验的结果来看，实验6对应的参数入口温度70℃、入口速度5 m/s、环境初始温度20℃,所消耗的成本最少，成本消耗为48.1元。综合考虑升温时间和成本等因素，烘干房模型最终选用实验6对应的参数。

4 结论

1)实验测得数据与仿真值，两者偏差并不大，验证了该方法对烘干房数值模拟的准确性。

2)经过分析，对烘干房结构进行优化，增加送风口和回风口的数量，并进行仿真实验。从实验结果看，烘干房内部气流组织的速度提高到0.9 m/s，同时温度上升到目标温度所需的时间减少了50 s。

3)在不同参数组合的情况下，利用正交试验的方法对优化后的烘干房进行仿真分析，以升温时间和成本消耗为目标，得到实验6方案(入口温度为70℃、入口速度为5 m/s、环境的初始温度为20℃时)消耗的成本最低(48.1元)。

4)因对烘干房模型进行简化处理，所以模拟仿真会有偏差。在以后的研究可以建立更加逼真的模型，还可从送风口排布方式上展开进一步研究。