基于跑道容量的航班恢复优化调度
2022-05-07严宇熊静陈聪聪杨益沁余佳莹
严宇 熊静 陈聪聪 杨益沁 余佳莹
摘 要:为了降低航班延误造成的经济损失,在机场平稳运行条件下提高航班运行效率。在原有的航班恢复模型基础上,引入航空公司公平性模型、跑道容量约束、快速过站约束和取消航班约束的航班运行的四种情况,建立顾及航空公司公平性的总成本最小的航班恢复目标函数,该模型适用于不同航班数限制的机场。算例中对长沙机场的某日4小时内的航班运行情况,使用飞蛾扑火算法得到优化方案,与机场原始航班平均运行成本相比,本文提及方法能降低机场的航班运行成本。
关键词:航班延误恢复;跑道容量;成本;航空公司公平性;飞蛾扑火算法
中图分类号:F560 文献标识码:A
Abstract: In order to reduce the economic losses caused by flight delays, the efficiency of flight operations should be improved under the conditions of stable operation of the airport. On the basis of the original flight recovery model, the airline fairness model, runway capacity constraint, rapid transit constraint and flight cancellation constraint are introduced, and the four situations of flight operation are established to establish a flight recovery with the smallest total cost that takes into account the fairness of the airline objective function, the model is suitable for airports with different flight restrictions. In the calculation example, for the flight operation situation of Changsha airport within 4 hours on a certain day, the moth fire suppression algorithm is used to obtain an optimized scheme. Compared with the average operation cost of the original airport flight, the method mentioned in this paper can reduce the flight operation cost of the airport.
Key words: flight delay recovery; runway capacity; cost; airline fairness; Moth-Flame optimization algorithm
0 引 言
近年來,随着航线及飞机数量的增加,世界各个国家和地区的机场地面和空中交通流量不断增长,目前在大部分中型以上机场产生了越来越严重的交通拥挤,一旦出现特殊情况,造成的航班延误也越来越严重,所以中国许多机场开始修建多条跑道来缓解交通堵塞造成的机场效率低下和航班延误问题。针对单跑道航班恢复问题的研究相对比较成熟,该类航班恢复模型适用范围不广,但对不同跑道数量和运行模式下航班延误恢复的研究相对较少,因此有必要对此问题进行深入的探讨分析。
针对航班恢复的研究,中外学者大多从航空公司角度出发,对于飞机、机组、旅客的逐一恢复和一体化恢复已经有较为丰硕的研究成果[1-3]。从机场角度出发,1997年,Gilbo[4]最早构建了考虑安全规则以及天气影响的单机场延误恢复模型;2004年,马正平等[5]建立了一种考虑跑道容量的航班延误优化模型;2008年,丁建立等[6]构建了机场大面积航班延误后的一种航班恢复模型;丁建立等[7]引入航线因子,综合考虑了航班延误造成的经济损失;2011年,刘艳红等[8]建立了只考虑显性损失的恢复模型;2014年,杨欢等[9]建立了机场航班优化调整模型,其中以机场成本、航空公司损失、旅客损失的加权最小化为目标函数;并在2017年首次提出了两阶段法即延误发生前和发生后的航班调度优化模型;汪虹宇[10]和杨顺秀[11]分别构建了航班延误后机场登机口和停机位的优化调度模型;2018年,宾云鹏等[12]考虑了各航空公司的公平性,构建了以旅客满意度为目标函数的机场航班延误恢复模型。
目前机场航班恢复问题的研究已经取得了一定的成果,但依然存在以下不足:(1)历史研究中的航班恢复模型大多只适用于跑道构型一定的机场,且未考虑到机场进出港之间相互影响,适用性不强;(2)在为航班安排合适的起飞和落地时间时,未考虑到航空公司的公平分配;(3)历史研究中,未考虑快速过站的情况;(4)未考虑机场的实际运行情况约束机场的航班取消;(5)在恢复过程中,未充分考虑航班的状态。
针对以上不足,本文将以航空公司公平性和成本最小化为目标函数。引入多跑道机场的容量约束,并结合机场航班快速过站,建立数学模型。选取我国某大型机场某日的航班实际运行,通过飞蛾扑火算法对提及模型进行求解。
1 问题描述与假设
本文研究的问题是考虑在机场容量限制下、多机型进行航班任务调整的航班恢复问题。在进行航班调整时,同时考虑航空公司的运行成本最小化和航空公司的公平性。
(2)不考虑机场的停机位容量;
(3)各航班的飞行时间是常量;
(4)飞机在机场均为降落—起飞。
2 模型建立
2.1 目标函数
针对多机型、多跑道机场的航班恢复问题,本文在兼顾机场航班运行成本最低的目标上,在考虑航空公司公平性的基础上建立目标函数。
2.6 航班取消数量约束
机场为保障旅客的权益,机场当日的航班取消的情况不得过多。因此,限制当天取消航班的航班数量不超过当天航班总数的20%。
3 模型算法
本文使用格里菲斯大学学者Mirjalili提出的飞蛾扑火算法(Moth-flame optimization algorithm,MFO)。
设次日所有的航班时刻集合为一个飞蛾位置,飞蛾的位置限制需满足约束条件限制,通过飞蛾扑火算法寻找目标函数最低的值。
针对飞蛾扑火算法存在的易陷入局部最优的问题及搜索效率问题,令飞蛾在靠近火焰时,通过指数递减策略,以达到平衡全局搜索和局部搜索的能力。
对基于跑道容量的航班恢复问题的求解的算法基本思路如下:
Step1:初始化算法参数,设置飞蛾种群大小,优化变量的维数,最大迭代次数以及初始火焰数量;
Step2:初始化飞蛾的位置;
Step3:计算每只飞蛾的适应度值,找出最优飞蛾个体赋给火焰;
Step4:更新每只飞蛾与火焰的位置,并记录当前最优火焰适应度值;
Step5:判断是否达到最大迭代次数,若达到则输出整个迭代过程中最优火焰位置以及对应的适应度值,算法结束。
4 算例分析
4.1 数据来源
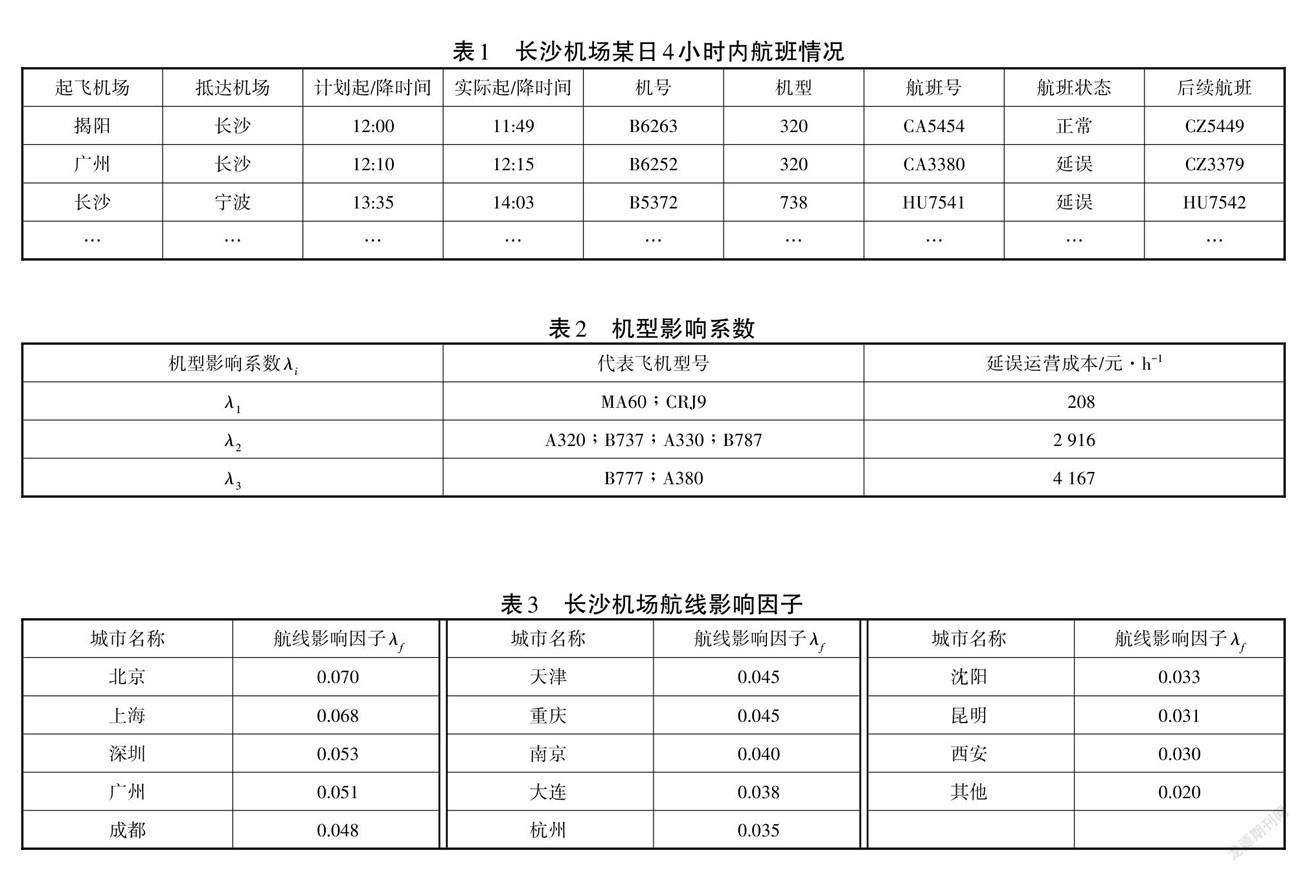
本文中以长沙黄花机场(CSX)为例,对本模型的有效性进行验证分析。选取长沙黄花机场在2021年某日12:00~14:00航班信息(共有60架次航班的起降),并舍去原取消航班去除误差,航班信息如表1所示。
在本文的目标函数中,机型影响系数λ与机型的类别有关,根据最大起飞质量、尾流类型将机型分为三类,如表2所示。
根据历史航线航班量大小和城市距离,通过景崇毅[15]在论文中提及因子分析法和聚类分析法,对选取时间段长沙机场涉及航班的航线因子λ进行计算并归一化处理,计算结果如表3所示。
4.2 测试结果分析
为验证本文提及模型的可行性,机场在12:15时,由于天气原因,机场的跑道容量由原来的30架/小时降低为20架/小时,通过对比实际航班恢复中航司航班均恢复成本和本文提及方法的航班均恢复成本,验证本方法的优势。
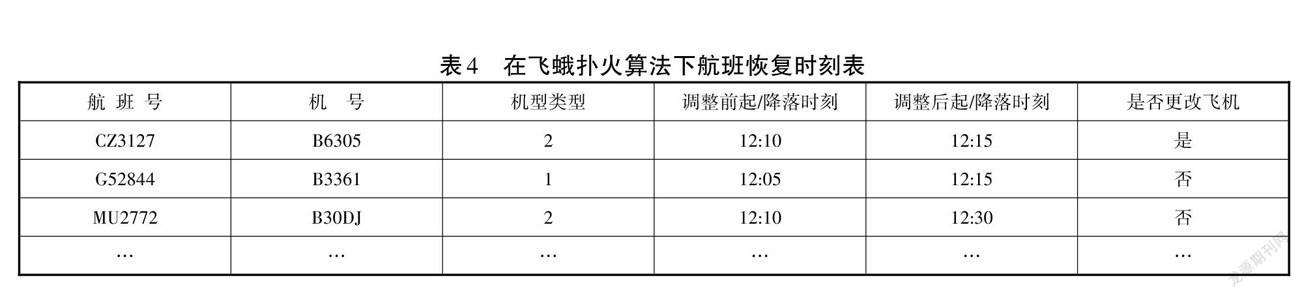
通过本文对航班进行恢复的结果如表4所示。
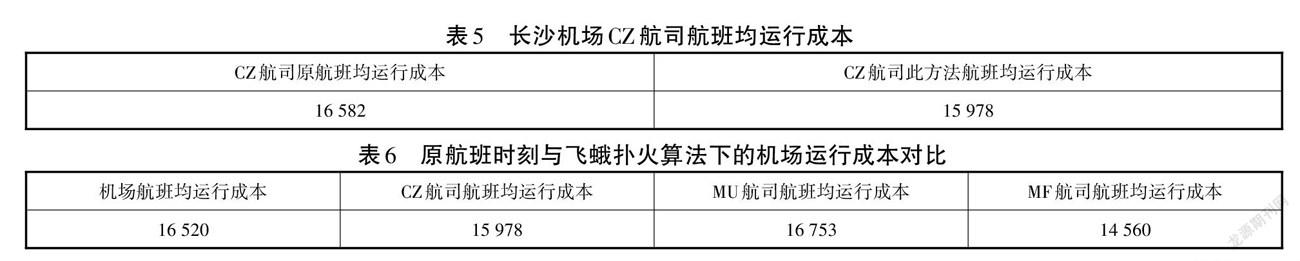
由于长沙机场12:00~14:00的航班涉及到15家航空公司,在此分析部分航企的航班均运行成本如表5、表6所示。CZ航司的航班均运行成本低于MU、MF航司及机场航班均运行成本,认为由于CZ航司在长沙机场建立了运行基地,因此航班均运行成本低。
5 结 论
本文主要建立了考虑航空公司公平性的机场航班成本最低模型,并设置机场跑道约束、航班快速过站约束等约束来模拟机场航班实际运行中的突发情况,最终利用飞蛾扑火算法计算航班的延误成本。最后对比原始机场航班的运行成本和航空公司公平性,本模型优化后航班运行时间较原始情况成本降低、公平性提高。
参考文献:
[1] 赵秀丽,朱金福,郭梅. 航空公司不正常航班机组恢复模型和算法研究[J]. 交通科学与工程,2010,26(4):76-79.
[2] 朱博,朱金福,高强. 飞机和机组一体化恢复的约束规划模型[J]. 交通运输工程学报,2013,13(1):77-83.
[3] 楊欢,庞明宝,吴维. 基于动态环境的机场航班实时调度优化研究[J]. 数学的实践与认识,2017,47(1):63-69.
[4] Gilbo E P. Optimizing airport capacity utilization in air traffic flowmanagement subject to constraints at arrival and departure fixes[J]. IEEE Transactions on Control Systems Technology, 1997,5(5):490-503.
[5] 马正平,崔德光. 机场航班延误优化模型[J]. 清华大学学报(自然科学版),2004(4):474-477,484.
[6] 丁建立,计金玲,黄剑雄. 基于免疫机制的航班延误快速恢复模型及实现[J]. 计算机工程与设计,2008(19):5029-5032.
[7] 丁建立,王新茹,徐涛. 航班延误恢复调度的混合粒子群算法[J]. 交通运输工程学报,2008(2):90-95.
[8] 刘艳红,高林,李耀华. 基于经济损失的航班延误恢复模型研究[J]. 中国民航大学学报,2011,29(1):46-50.
[9] 杨欢,庞明宝,陈静. 基于航班延误的机场调度调整优化研究[J]. 河北工业大学学报,2014,43(5):101-105.
[10] 汪虹宇. 航班延误后恢复及登机口资源调配研究[D]. 南京:南京航空航天大学(硕士学位论文),2017.
[11] 杨顺秀. 面向延误情景的机场停机位优化调度研究[D]. 西安:西安理工大学(硕士学位论文),2018.
[12] 宾云鹏,邵荃,姜柯,等. 基于旅客满意度与公平性的机场航班计划恢复[J]. 科学技术与工程,2018(14):275-278.
[13] Bengi Manley, Lance Sherry. Analysis of performance and equity in ground delay programs[J]. Transportation Research Part C, 2010,18(6):910-920.
[14] 孙海勇,刘裕旭. 不同运行模式下的远距平行跑道容量研究[J]. 航空计算技术,2019,49(5):59-62,66.
[15] 景崇毅,孙宏. 基于因子分析和聚类分析的航线市场细分方法[J]. 湘潭大学自然科学学报,2013,35(1):122-126.
收稿日期:2021-07-25
作者简介:严 宇(1997-),男,江苏南京人,上海工程技术大学航空运输学院硕士研究生,研究方向:优化算法、交通运输规划;熊 静(1979-),女,江西九江人,上海工程技术大学航空运输学院,副教授,硕士,研究方向:民航信息工程;陈聪聪(1995-),女,江苏徐州人,上海工程技术大学航空运输学院硕士研究生,研究方向:交通运输规划与管理;杨益沁(1997-),女,上海人,上海工程技术大学航空运输学院硕士研究生,研究方向:交通运输规划与管理;余佳莹(1995-),女,辽宁鞍山人,上海工程技术大学航空运输学院硕士研究生,研究方向:交通运输与规划管理。
