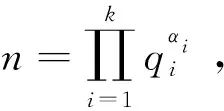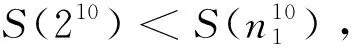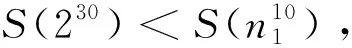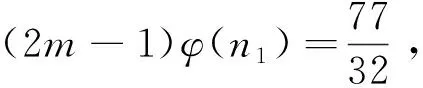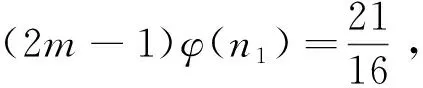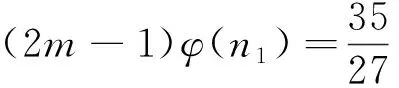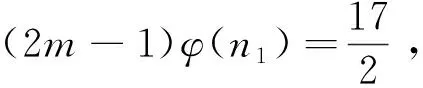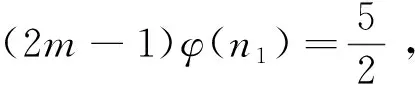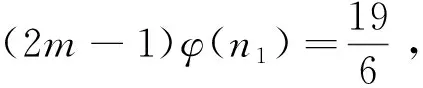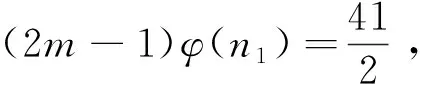数论函数方程mφ(n)=φ2(n)+S(n10)的解

2022-05-06郑惠

江西科学 2022年2期

关键词：数论正整数情形

郑惠

(阿坝师范学院数学学院，623000，四川，汶川)

0 引言

本文将讨论在L=10时，当M=N=1，数论函数方程

mφ(n)=φ2(n)+S(n10)

(1)

的可解性，并利用初等方法给出了方程的全部正整数解。

1 主要引理

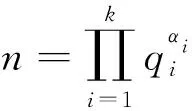
引理2[2]：当n≥3时，有φ2(n)=φ(n)/2。

引理3[2]：当n≥3时，有φ(n)为偶数。

引理4[17]：对于素数p和正整数k，有S(pk)≤kp；特别地，当k

2 定理及证明

定理1：方程(1)只有在m=1、2、4、6、8、11、13时有正整数解，且1)当m=1时，方程(1)有正整数解n=1、320、441、882、1 681、3 362；2)当m=2时，方程(1)有正整数解n=81、147、162、196、294；3)当m=4时，方程(1)有正整数解n=27、54；4)当m=6时，方程(1)有正整数解n=16、33、44、66；5)当m=8时，方程(1)有正整数解n=9、18；6)当m=11时，方程(1)有正整数解n=7、14；7)当m=13时，方程(1)有正整数解n=2。

(2m-1)qα-1(q-1)φ(n1)=2S(n10)=2S(q10α)

(2)

下面根据q的不同取值情况，对方程(2)进行分类讨论。

情形1：当q=2时。

若α=4，由式(2)有8(2m-1)φ(n1)=2S(240)=88。根据引理3有2m-1=11且φ(n1)=1，则m=6，n1=1,2，所以n=16、32。经过检验n=16是方程(1)的解。

若α=6，由式(2)有32(2m-1)φ(n1)=2S(260)=128。根据引理3有2m-1=1且φ(n1)=4，则m=1，n1=5，所以n=320。经过检验n=320是方程(1)的解。

若α=9，由式(2)有256(2m-1)φ(n1)=2S(290)=192，这是不可能的，故此时方程(1)无解。

若α≥10，由式(2)与引理4有2α-1(2m-1)φ(n1)=2S(210α)≤40α，这是不可能的，故此时方程(1)无解。

综上所述，在该种情形下方程(1)只有2个解。即：仅当m=6时，n=16；仅当m=1时，n=320。

情形2：当q=3时。

若α=2，由式(2)有6(2m-1)φ(n1)=2S(320)=90。根据引理3有2m-1=15且φ(n1)=1，则m=8，n1=1、2，所以n=9、18。经过检验n=9、18是方程(1)的解。

若α=3，由式(2)有18(2m-1)φ(n1)=2S(330)=126。根据引理3有2m-1=7且φ(n1)=1，则m=4，n1=1、2，所以n=27、54。经过检验n=27、54是方程(1)的解。

若α=4，由式(2)有54(2m-1)φ(n1)=2S(340)=162。根据引理3有2m-1=3且φ(n1)=1，则m=2，n1=1、2，所以n=81、162。经过检验n=81、162是方程(1)的解。

若α≥6，由式(2)与引理4有3α-1(2m-1)φ(n1)=S(310α)≤30α，这是不可能的，故此时方程(1)无解。

综上所述，在该种情形下方程(1)只有6个解。即：仅当m=8时，n=9、18；仅当m=4时，n=27、54；仅当m=2时，n=81、162。

情形3：当q=5时。

若α≥4，由式(2)与引理4有4·5α-1(2m-1)φ(n1)=2S(510α)≤100α，这是不可能的，故此时方程(1)无解。

综上所述，在该种情形下方程(1)无解。

情形4：当q=7时。

若α=1，由式(2)有6(2m-1)φ(n1)=2S(710)=126。根据引理3有2m-1=21且φ(n1)=1，则m=11，n1=1、2，所以n=7、14。经过检验n=7、14都是方程(1)的解。

若α=2，由式(2)有42(2m-1)φ(n1)=2S(720)=252。根据引理3有2m-1=1且φ(n1)=6，或2m-1=3且φ(n1)=2，则m=1，n1=9、18；或m=2，n1=3、4、6。所以m=1，n=441、882；或m=2，n=147、196、294。经过检验n=147、196、294、441、882都是方程(1)的解。