基于ARIMA与SEIR模型的突发传染病发病特征与趋势预测

谢小良，王时雨，成佳祺，朱志远

(湖南工商大学 理学院，湖南 长沙 410205)

一、文献综述

突发传染病不但损害人民群众的生命健康，而且可能给经济发展以及社会稳定带来严重的影响。因此，突发传染病防控一直是各级政府和社会公共卫生治理中的重中之重。在人类发展历程中，人们一直与突发传染病作斗争，写下了一幕幕令人辛酸的历史，如2003年“非典”，2014年埃博拉病毒以及2019年新型冠状病毒等都给人类造成了严重的影响。对传染病发病趋势进行预测，能够帮助我们及时有效地采取相应措施进行疫情防控，对于人类健康与生命安全保障具有重要的现实意义。

在国内外的传染病疫情预测研究中，主要是从以下两个方面进行深度分析：一是基于时间序列预测模型进行传染病预测。目前，预测研究中ARIMA模型应用比较广泛，其主要针对时间序列数据分析其特征并预测未来走向，如杨霜等(2021)[1]通过ARIMA乘积季节模型来预测红细胞临床用量，为医院中血液管理提供切实可行的依据。张帆等(2021)[2]基于传统的ARIMA模型将其与SVM相结合对道路交通伤害死亡率进行了预测，预测结果发现，相较于ARIMA模型，其模型精度更高，更适用于预测道路交通伤害死亡率。而在针对传染病发病预测的研究中，ARIMA模型仍发挥着重要的作用。田庆等(2021)[3]针对山东省结核病的相关特征，采用ARIMA模型结合其季节性与趋势性对发病趋势进行拟合和预测。模型拟合情况较好，精度较高，能够较好地反映出山东省结核病的发病走向。彭阳和卢千超(2021)[4]则是在ARIMA模型的基础上分析河南省南阳市手足口病的特征进而进行季节性差分，提高了模型预测精度，从而能够更好地预测南阳市手足口病的发病人数，为疫情防控工作提供依据。刘继恒等(2017)[5]选取了季节趋势模型与ARIMA乘积季节模型对丙类传染病进行了定量分析并以此构建丙类传染病的预测模型，使得被动预防变成主动预防，丙类传染病的预防工作能够更加有效地进行。余艳妮等(2018)[6]研究了目前普遍用于公共卫生及传染病防控的数学模型以及统计学方法。传统模型主要包含ARIMA模型以及回归模型，但回归模型影响因素过多所以一般采用时间序列构建模型，其次是以传染病传播动力学为理论的基础模型构建；此外，应用以大数据、人工智能为工具的传染病预测模型也是当今学界普遍采用的方法。二是基于传染病动力学模型进行预测。如按照传染病的特点进行划分的SI、SIS、SIR、SIRS以及SEIR 模型，其中SEIR模型应用较为广泛，其包含的传染病特征较多，能够更好地反映传染病传播过程中各类人群的变动情况。如Wilfredo等(2021)[7]通过分析早期的冠状病毒和冠状病毒类似暴发的早期阶段的特征，对SEIR的参数进行调整，使其能够更加有效地预测冠状病毒类传染病的传播趋势。Vinicius(2021)[8]在SEIR模型的基础上提出了一个非线性算法，能够更加有效地模拟疫情传播情况。钟南山院士团队利用SEIR模型和机器学习法预测国内疫情将于2022年2月底达到顶峰[9]。除了对传染病进行研究，SEIR如今也在拓展应用领域，如曹广和沈丽宁(2022)[10]结合网络医疗众筹传播的特征在SEIR模型的基础上进行建模并仿真分析，仿真结果显示模型拟合精度较高，能够有效反映出医疗众筹的传播过程。马宇彤和胡平(2021)[11]在分析问答社区的传播机制后对SEIR模型进行改进，应用结果发现改进后的SEIR模型更加适用于描述知识传播规律。

综上所述，国内外学者应用ARIMA与SEIR模型对突发传染病进行预测研究，目前大部分研究是基于传染病的相关特征，分析传染病的特征信息，进而选取较为合适的预测模型对传染病传播情况进行预测。在传统的时间预测模型中，ARIMA模型在传染病预测方面的应用较为广泛，通常是基于传染病疫情中发病人数的时间序列数据进行模型拟合并预测，而在传染病传播动力学预测研究中，SEIR模型相较于其他模型应用广泛，是在基于传染病传播基本要素构建相关指标的基础上进行数据拟合并预测。目前少有将两者进行比较分析的，基于此本文选取某市30天突发传染病疫情的变动情况，分别基于ARIMA模型和SEIR模型进行数据拟合并预测其发展动向，将两者的预测结果进行比较分析，为疫情防控工作提供切实可行的依据，并为今后的传染病监测与预警研究奠定坚实的基础。

二、 传染病发病特征分析

以2018年1月到2020年12月以来某国传染病发病数为样本，运用统计软件绘制折线图，分析结果如图1所示。

图1 某国传染病发病数年度分布图

从图1可以看出，传染病发病呈现某种波动的形式，有着季节性的特征，而特别需要注意的是每年的1月与2月，是传染病高发时期，春节期间，人员大量流动，给传染病传播提供了有利条件，因此需格外注意1月到2月的传染病防控[12]。

针对某国2018年1月到2020年12月法定传染病的发病数以及死亡人数，计算得到2018年1月到2020年12月的传染病发病死亡率，如图2所示。从图中能够看出，从2018年1月到2020年2月这段时间，传染病发病死亡率是在0.3%的上下波动，而2020年2月传染病发病死亡率达到最高(1.158%)，之后逐渐下降，最终在0.4%的上下波动。根据目前该国疫情情况来看，2020年2月传染病发病死亡率飙升的主要原因是新型冠状病毒所导致的重大突发卫生事件，疫情防控没能及时采取措施，疫情规模迅速扩大，使得该国传染病死亡人数迅速增加。

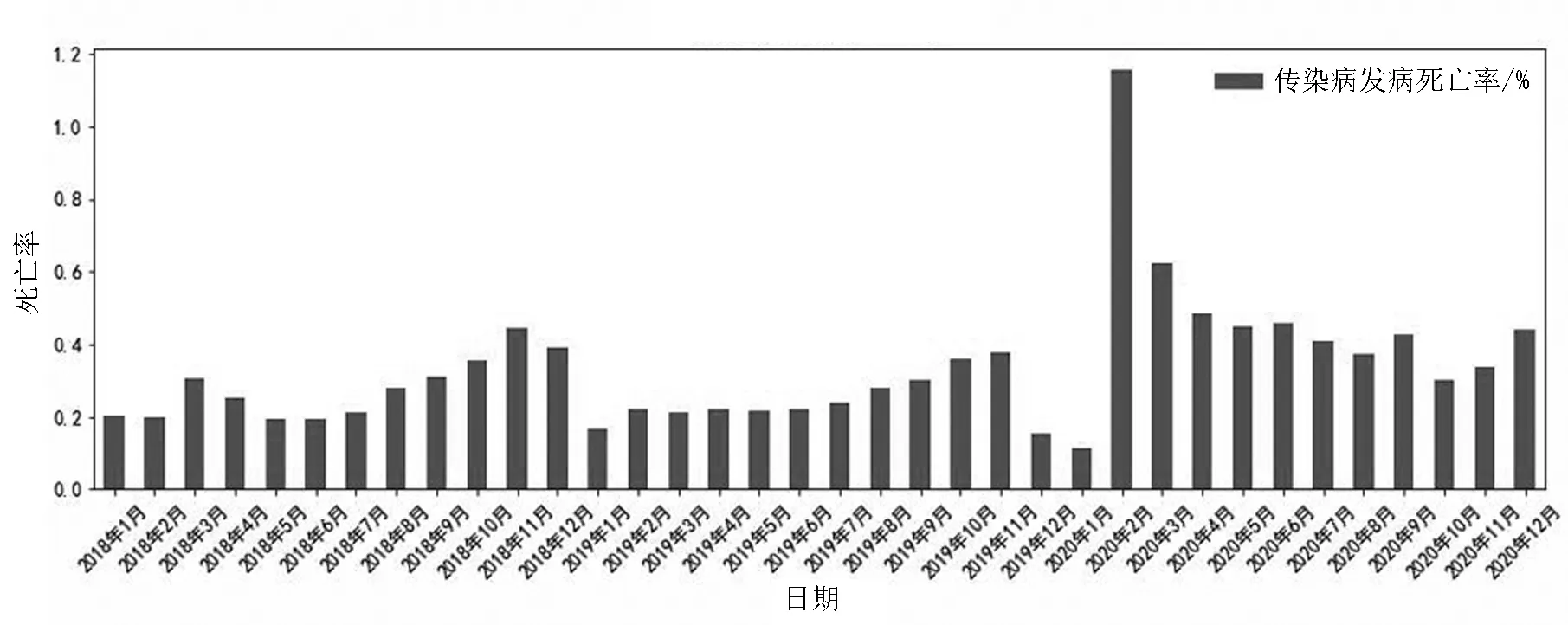
图2 某国传染病发病死亡率年度分布图

传染病传播的过程不仅涉及时间、空间，还波及人群[13]，三者的分布情况确定了传染病疫情的规模，而要采取及时有效的措施进行疫情防控，最主要的是透析传染病传播的本质进而可在此基础上进行针对性的有效监管与处理。传染病传播是由传染源、传播途径以及易感人群三个环节组成的，缺少其中任一环节传染病就无法传播开来，因此可针对三个传染病环节进行疫情防控管理。分析各个环节可以发现传染病的传播不仅会受到自然因素的影响，也会受到社会因素等人为因素影响。如传染病的传播途径通常指的是病原体传播的方式及过程，通常病原体可以依附在某些介质上，其本身不一定能寄生在介质上，但可以通过该种介质将自身传导到受感染者，按照介质的种类不同可以划分病原体的传播途径，如水、土壤、食物、空气，抑或者病原体携带者，故而常见的传播途径有水土传播、空气传播、接触传播等，此外，传染病传播途径往往不局限于一种，可以通过多种方式进行传播扩散。通过对传染病传播途径进行分析，详细了解并分析病原体传播过程中的影响及相关因素，通过对相关因素进行初步分析有利于传染病模型的构建以及对传染病传播的宏观分析。

三、ARIMA与SEIR模型分析

(一)ARIMA预测模型

常用时间序列模型有七种，分别为朴素法、简单平均法、移动平均法、简单指数平滑法、霍尔特线性趋势法、霍尔特-温特斯法以及本次使用的ARIMA预测模型，ARIMA模型全名为自回归积分滑动平均模型，于20世纪70年代由Box和Jenkins提出的一种时间预测模型，故该预测模型又称Box-Jenkins模型法，该模型主要基于对发展趋势或周期性数据的描述，其旨在利用描述数据之间的相关性进行预测分析，适合疾病发病率、GDP、市场销售额等有明显时间先后变化趋势的数据分析。而以时间顺序排列的数据序列称为时间序列(Timeseries，{x,t=1，2，…，n})，模型采用的数据序列的主要特点，一是随时间t变动而改变，二是变量之间并非相互独立，而这些随机变量所具备的自相关性一定程度上代表着发展的延续性，将自相关性以系数等形式在模型中表述出来就可以通过时间序列的实际值预测未来值，而ARIMA模型包括自回归AR模型、移动平均MA模型、自回归移动平均ARIMA模型以及复合季节SARIMA(ARIMA)模型。

ARIMA求和自回归移动平均模型数学表达式简称为ARIMA(p,d,q)模型：

(1)

其中Φ(B)=1-φ1B-φ2B2-…-φpBp,Θ(B)=1-θ1B-θ2B2-…-θqBq，

∇=1-B表示差分算子，p为时间序列自回归阶数，d为模型差分次数，q为移动平均阶数，B为延迟算子。

ARIMA时间序列模型预测的建模过程[14]有以下4个关键步骤：

(1)时间序列数据预处理：通过观察时序图，判断时间序列的趋势与周期性是否显著，同时进一步观测自相关系数与偏自相关系数确定结论，并做单位根检验判断序列是否平稳；使用BOX检验判断是否为白噪声序列，确保序列非随机。

(2)ARIMA模型识别：根据差分后序列，通过分析其自相关及偏自相关图性质，为模型确定合适的p、q值，对模型进行初步拟合，对识别阶段提供的粗模型进行参数估计并假设检验。

(3)模型诊断：判断参数是否具有统计学意义，残差是否为白噪声序列。

(4)模型预测：利用拟合模型进行对未来值的预测，判断时序图未来趋势，对模型效果以及价值做出基本分析。

(二)SEIR预测模型

SEIR模型对指标构建按研究对象划分为S、E、I、R等4种指标[15], 其具体表达式为：

(2)

其中，S为易感群体，易感群体并非直接与N总人数等值，其表示潜在的可能受感染群体，该群体代表能够与感染群体直接接触或处于易受感染状态，这种存在被病毒感染的概率并且概率不为0的群体即为易感群体。

E为潜伏群体，病毒携带者呈阳性结果但是没有出现感染症状的群体。

I为感染群体，病毒携带者呈阳性结果并且出现感染症状的群体，个体作为传播源而独立存在，并有一定概率将病毒传染给易感群体。

R为治愈群体，治愈群体并非完全由病毒治愈者构成，为排除死亡群体与有效隔离群体而将这些因素囊括在内，作为治愈群体存在。

r为感染者平均接触的数量，β为接触发病者感染概率，β1为接触潜伏者感染概率，α为潜伏期到发病的转化率，m为治愈率。

SEIR传播过程如图3所示：

图3 SEIR传播过程示意图

四、 突发传染病发病趋势预测

(一)数据来源及描述性统计分析

选取2020年暴发的某突发传染病疫情，将该时期突发传染病导致的某国疫情作为目标对象，对其发病状况进行拟合，进而预测发病趋势。选取2020年2月17日到2020年3月18日这段时间某国所公布的相关数据，选取其中某市的累计确诊人数、死亡人数以及治愈人数，从掌握疫情基本规律的基点出发，将数据可视化，并进行统计分析与模型预测，以实现对未来疫情发展的预测与监控。对该市疫情在2020年2月17日到2020年3月18日的概况进行描述性分析，结果如图4所示。

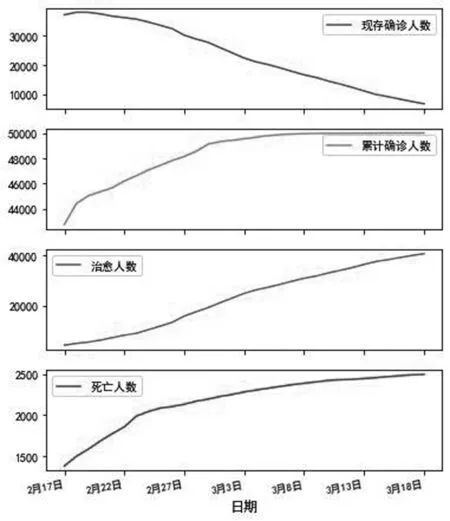
图4 某市传染病综合发病概况统计数据

由图4可知，在2020年2月17日到2020年3月18日期间，该市现存确诊人数逐渐递减，先缓慢减少，中期递减速率加快，末期速率减缓。累计确诊人数与死亡人数趋势走向较为相似，一直在递增，但递增速率在逐渐减缓，而治愈人数一直在增加，且速率也在逐步加快。

根据已有研究可知导致疫情发生的是一种高致病性的冠状病毒，其不仅潜伏期较长，且其传染性极高，可通过呼吸道飞沫传播以及接触传播，且接触病毒污染的物品也有很大概率被病毒寄生，对于无防范措施的人群而言，是极易被感染的，同时经过时间的推移其传染源很难被发现，其暴发时期正值春节期间，社会流动频繁，在政府采取措施积极应对的情况下，降低人群流动量，同时进行隔离切断该类病毒的传播，有助于降低疫情暴发的规模[16]。

结合以往的传染病研究， 将“现有疑似/前日观察”视作被观察者出现疑似症状的概率，而“新增确诊/前日疑似”视作疑似症状者患病的概率，该市每日观察人数是通过该市确诊人数占其所属省份确诊人数的比例与其所属省份观察人数的乘积计算得到的，基于此计算该市从2月17日到3月28日这段时期观察者出现疑似症状的概率和疑似症状者患病的概率，其传染病发病指标变化情况如图5所示。

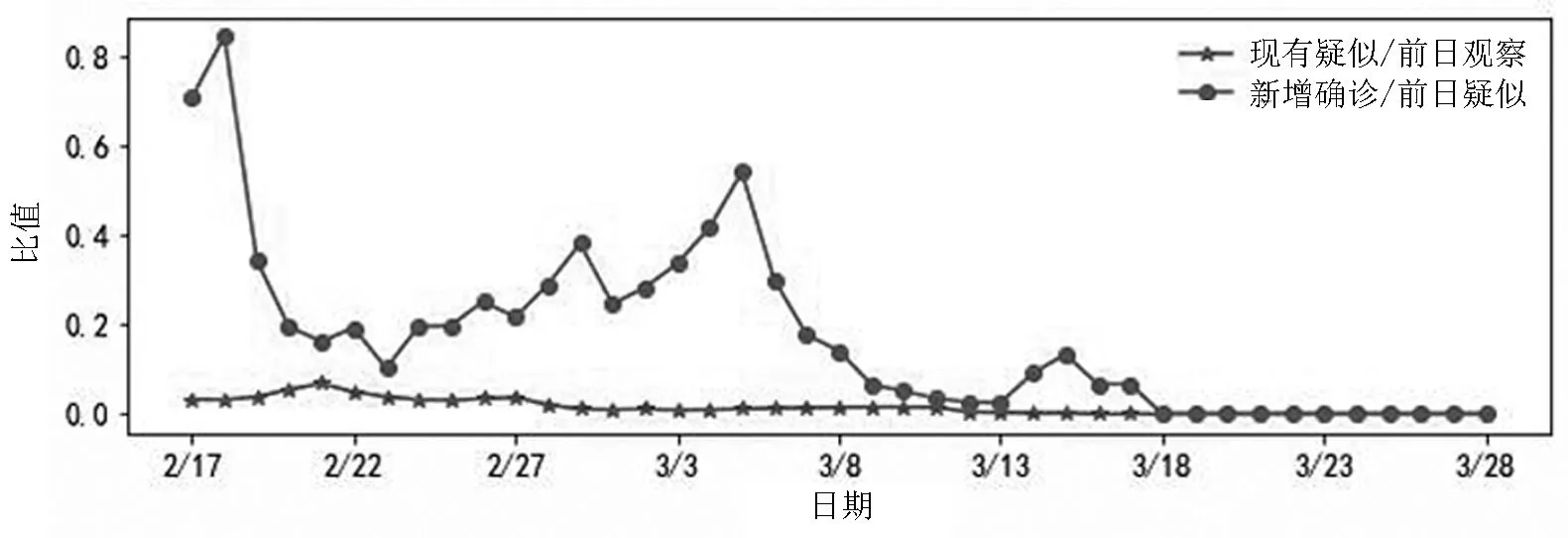
图5 发病指标时间序列变化走势图

如图5所示，观察群体出现疑似症状概率从最初的3.32%逐步降低趋向于0，疑似症状者患病的概率也从70.64%开始逐步降低至0，则可知该突发传染病感染可能性在不断减少，而疑似症状者患病概率与观察者出现疑似症状概率与实际患病概率相关，由折线图可以发现，该概率值有较强波动，这说明前日疑似人数对新增确诊的转化率受到其他因素影响，例如疑似患者是否与患病者有过直接接触等。从2020年3月18日到3月28日这段时间观察者出现疑似症状的概率和疑似症状者患病的概率都为0，则这段时期的发病人数等于确诊人数。

(二)突发传染病发病趋势分析

1.ARIMA预测模型

假设：传染病发病人数=确诊人数+尚未确诊的感染人数，其中尚未确诊的感染人数用“(现有观察人数×被观察者出现疑似症状的概率+现有疑似人数)×疑似症状者患病的概率”计算得到的结果近似代替，仍以上述样本国为例，选取2020年2月17日到2020年3月18日的发病人数作为目标变量，以发病人数的变动趋势来反映传染病疫情规模，对该时间序列数据进行平稳性检验，检验结果如图6所示。

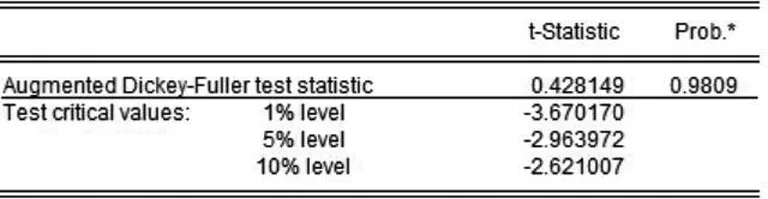
图6 单位根检验结果图

由图6可知在1%，5%，10%的显著水平下，都接受原假设，即发病人数时间序列数据具有单位根，是非平稳时间序列，需要对原始数据进行差分，使得处理过后的序列数据具有平稳性。

二阶差分结果如图7所示，二阶差分后的序列数据总体呈现出一种波动性，在0刻度上下波动。且其单位根检验得到的p值近似于0，则拒绝原假设，即二阶差分后的序列数据是平稳序列。

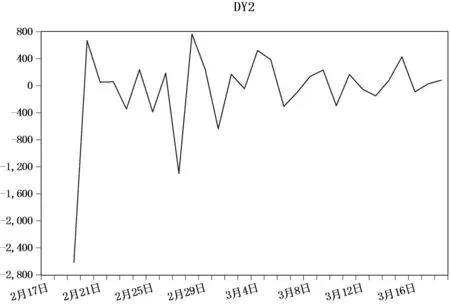
图7 二阶差分折线图

从图8可以知道二阶差分后的序列数据的自相关与偏自相关均表现为截尾，因此可将预测模型设立为ARIMA(p,2,q)，经过一系列的模型试验可得p=1,q=1,则针对此突发传染病，该市传染病预测模型为ARIMA(1,2,1)。对模型参数进行拟合，结果如图9所示。

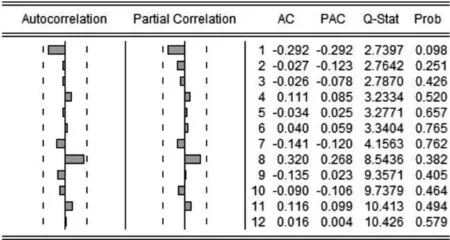
图8 自相关与偏自相关图

图9 ARIMA拟合结果图

由图9可知模型表达式为：

yt=0.9612yt-1+ut+0.7499ut-1。

为验证所构建模型的准确性，根据残差的白噪声检验结果对模型准确度进行检验，若检验结果是显著的，则说明模型拟合精度较低，反之则说明模型拟合情况较好，可对未来情况进行预测。绘制模型残差的自相关与偏自相关图进行验证。采用拟合的ARIMA(1,2,1)模型得到该自回归移动平均模型的残差，使用Eviews计算得到残差序列，通过对残差平方的自相关系数与偏自相关系数进行检测，其自相关与偏自相关图如图10所示，其自相关统计量以及偏自相关统计量检验结果都不显著，故不存在自相关性，则该残差序列为白噪声。因此可知该模型具有有效性，可以依据模型做未来值的预测。

图10 残差平方的自相关与偏自相关图

基于ARIMA(1，2，1)预测模型对后10天的发病人数进行预测，并与实际值进行对比，其综合测算结果如表1所示。

从表1中能够看出实际值与预测值的误差具有波动性，最后计算出预测10期的平均绝对误差为168.74，平均相对误差为5.13%，相对较小，可知模型预测精度较高。由此可知该市发病人数预测模型的拟合效果较好，预测结果表明在2020年3月19日到2020年3月28日之间该市现有发病人数逐渐递减，下降速率逐渐趋于平缓，与实际情况相符合。

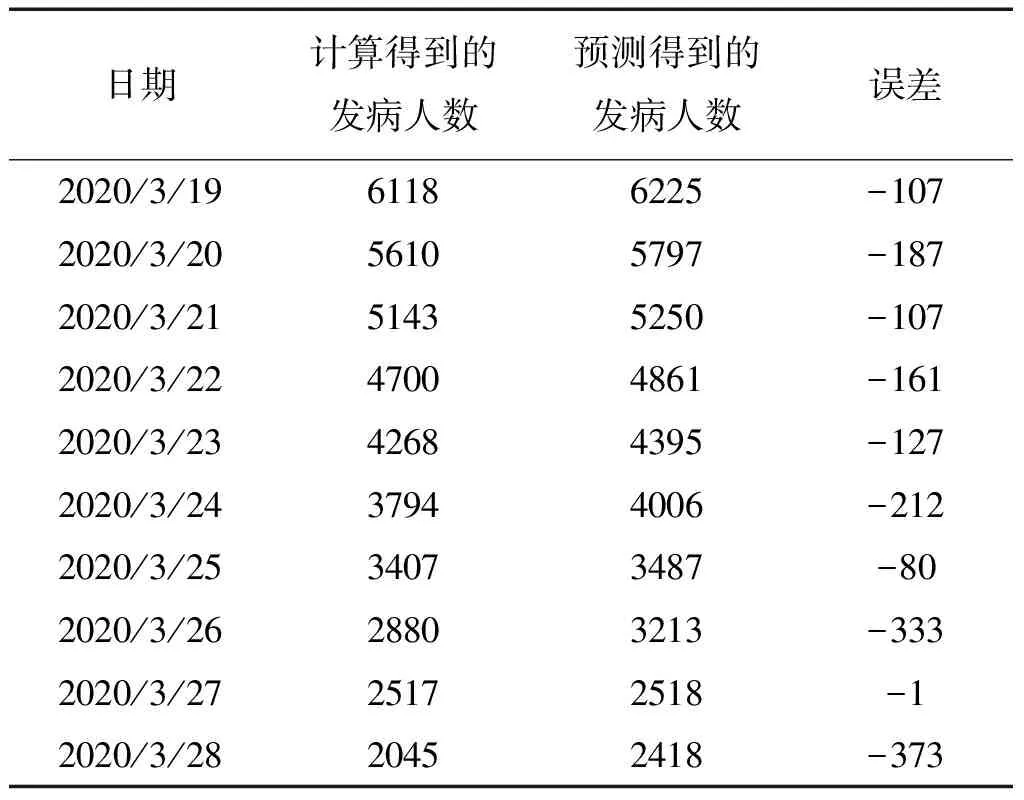
表1 传染病发病人数预测表

2.SEIR传染病预测模型

此突发传染病导致的疫情具备一般传染病的基本性质，基于其存在病毒潜伏期的性质，故在传统SIS以及SIR模型基础上添加潜伏期相应指标，对潜伏群体进行趋势刻画，更准确地展示出疫情发展动态。

通过收集2020年1月20日至3月31日某国发生的该突发传染病相关数据，包括累计确诊人数、重症人数、病故人数、病愈人数、现有疑似病例、累计追踪人数、当日解除追踪监控数以及观察中人数等，根据这些基础指标对其发病情况图像化。其中，现有确诊数=累计确诊数-累计病故数-累计病愈数。

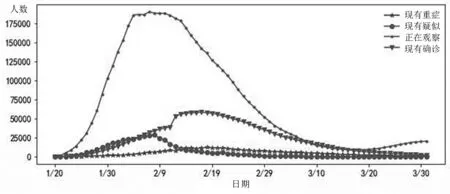
图11 某国各群体的发病情况的变化趋势

如图11所示，某国现有重症人数以小幅度趋势上涨，至2月19日左右达到峰值11864人，其后重症人数不断下降，因为政府通过大力建设医疗设施，确保患病重症者得到治疗，并且病情轻者病情得到控制；而现有确诊也是呈上涨趋势，至2月19日左右达到峰值，说明疫情初期政府对疫情管控从2月19日起初见成效，而2月10日左右由于现有疑似病例的确诊，使得实际确诊人数突然上涨。正在观察人数是通过大数据对疑似病例以及确诊患者的接触人群进行监控，该部分群体有较大概率成为疑似病例以及感染者，从1月20日至2月9日左右是返乡高峰期，由于疫情初期未能及时管控人群流动导致疫情传播，而各地方发布的疫情出行禁令使得人口流动降低，正在观察人数得到控制并有效降低。

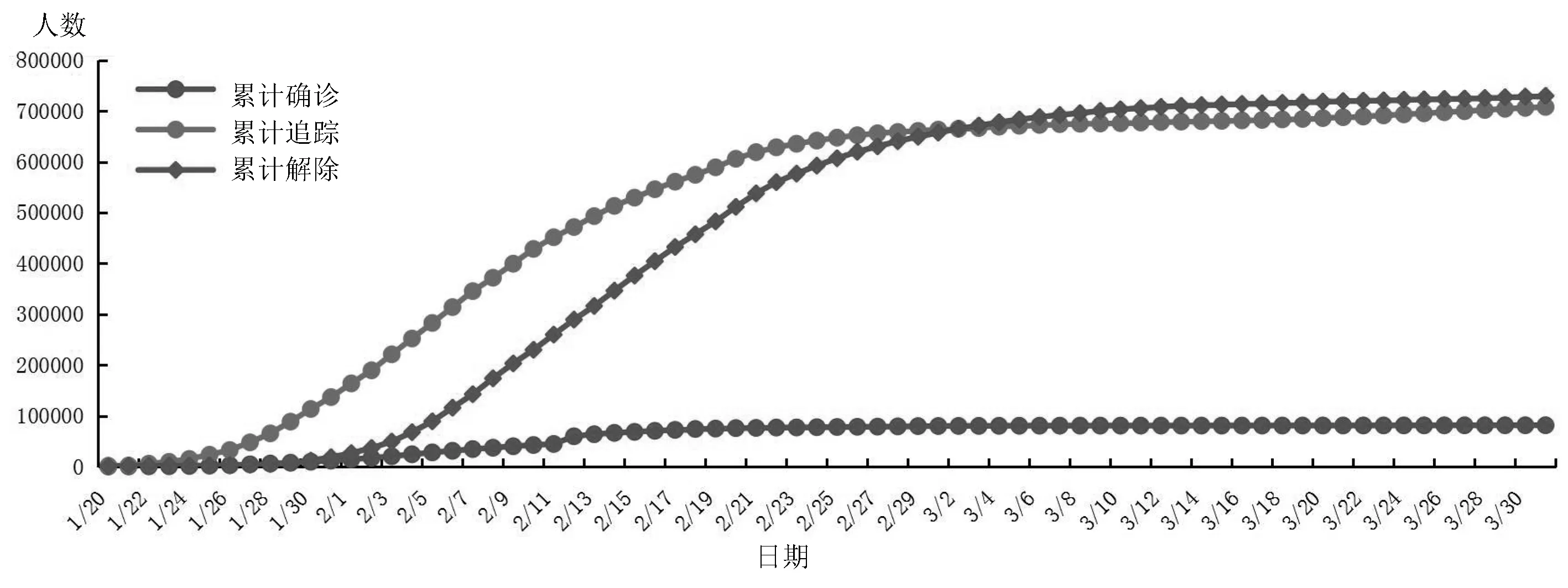
图12 某国疫情监控情况

选取累计确诊、累计追踪以及累计解除指标反映某国疫情监控情况，如图12所示，累计追踪数在3月3日前一直大于累计解除数，故在3月3日前累计监控人数在不断上升，累计追踪一定程度上可以表示为监控强度，累计解除一定程度上可以表示为排查强度，故可以认为3月3日起排除力度高于监控强度，疫情得到有效监控以及管控，可以看出3月3日拐点处累计确诊人数得到有效控制，增长幅度微不足录。

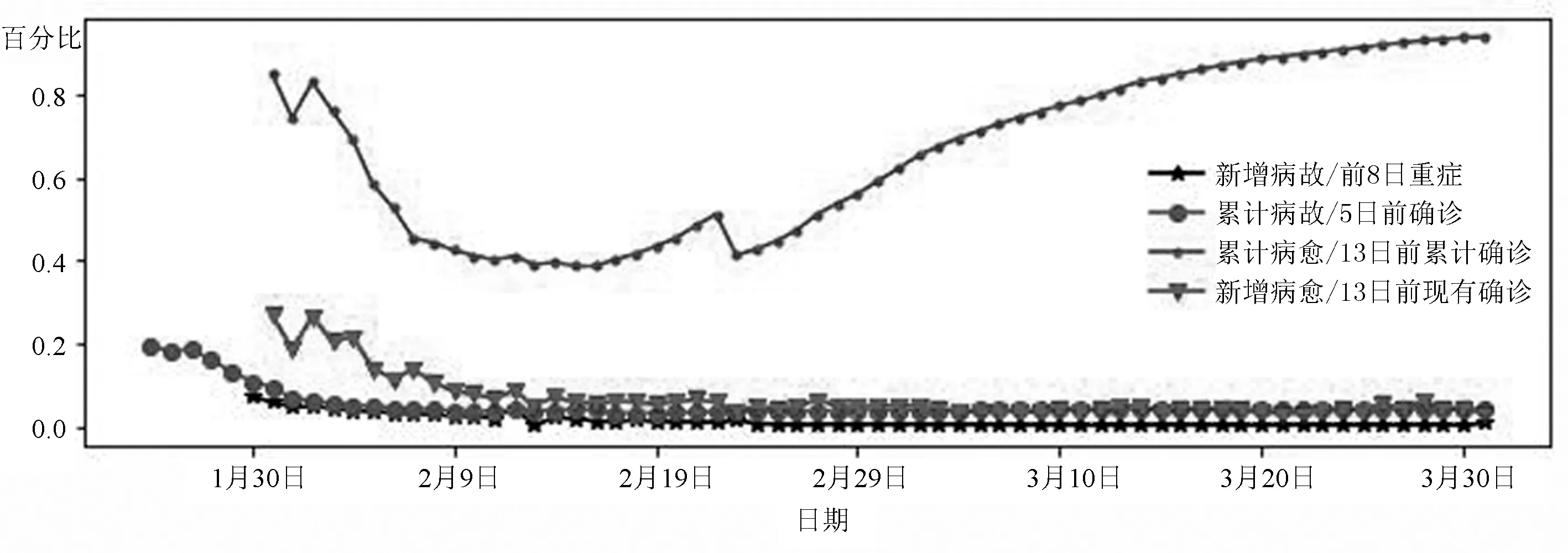
图13 指标时间序列变化走势图

为了统计患者的治疗情况，根据病毒潜伏期和重症患者治疗时间以及从确诊到病故时间，将“新增病故/前8日重症”视作重症患者死亡率，“累计病故/5日前确诊”视作患者死亡率，而由于治愈平均周期在13天左右，故将“累计病愈/13日前累计确诊”视作实际治愈率，“新增病愈/13日前现有确诊”视作疫情治愈率，如图13所示。通过图像观察发现重症患者死亡率与患者死亡率基本吻合，说明轻度患者基本上不存在死亡可能性，而死亡率从一开始的20%降低至0值取决于医疗水平以及病毒得到有效掌控，而实际治愈率由一开始的85%降低至40%左右再后来超过90%，说明对于该突发传染病已有有效的治愈方案，同时治愈率稳定在5%左右，一方面是医疗物资的限制，另一方面是患者人数稳定在一定数量。

通过对以上数据分析观测疫情发展动态，同时通过收集数据，根据现实背景计算SEIR模型所需指标，例如易感群体、感染群体、潜伏群体、治愈群体等基本指标，其次如发病者传播病毒概率(接触发病者感染概率)、潜伏者传播病毒概率(接触潜伏者感染概率)等，方便对SEIR模型的构建。

SEIR模型建立的关键在于对各参数值的设置，参数值设计必须参考实际情况。

通过收集数据得知截至2019年末，疫情暴发初期该市常住人口数有1121.2万人，令总人口数N=11212000。

S0参数为初期易感人群，令S0=N-E0-I0-R0；

I0参数为初期发病人数，发病源由于未知，初期病毒携带者人数未知，故令I0=1；

E0参数为初期潜伏人数，由于与病毒携带者接触群体数量未知，故令E0=10；

R0参数为初期治愈人数，病毒暴发初期治愈人数为0，故令R0=0。

rβ代表接触发病者感染概率，rβ1代表接触潜伏者感染概率，r为发病者接触的人数，根据以往研究将疫情发病情况分为无政府干预的传播情况与基于政府干预后的传播情况[17]，在结合12月8日至1月13日、1月14日至1月23日，1月24日至2月2日，2月3日至2月12日以及2月13日至3月18日的全国和该市各类人群的变动情况将rβ的值按时间段规定为0.659、0.487、0.235、0.125以及0.22，rβ1的值分别为0.282、0.243、0.202、0.132以及0.022。r的值分别为20人、15人、10人、5人以及3人。将12月8日至1月13日的参数赋予无政府干预状态，而政府干预则按时间段进行参数拟合。

α代表潜伏期到发病的转化率，而该类病毒的潜伏期最短为7天，最长为14天，故决定将潜伏期设为10天，则α的取值为潜伏期的倒数，得到α=0.1。

m代表治愈率，计算新增病愈/13日前现有确诊的平均数即为治愈率，m=0.046。

通过Matlab语言构建模型进行模拟，可以得到该类病毒传播过程中各群体随时间的变化趋势。如图14、图15所示。

图14 无政府干预下的SEIR模型拟合结果图

在政府干预的情况下，在不同的时间节点上对疫情规模产生了重要的影响，选取重要的干预措施进行分析，分别于1月13日、1月23日、2月2日以及2月12日时间点对参数进行调整。接触发病者感染概率在前四个时间段一直在不断下降，而由于2月12日公布的诊断标准将临床诊断病例数纳入确诊病例数进行公布，则相对的其接触发病者感染概率会上升，而接触潜伏者感染概率在各项政府措施的实行下不断减小，其中“四类人群”集中收治与隔离且医疗条件大大改善，将诊断标准纳入临床诊断确诊方法对接触潜伏者感染概率的影响程度较大。由图15可知，在政府干预情况下疫情的规模下降了两个数量级，而潜伏人数以及发病人数都提前到达峰值，且从图15中各指标发展趋势可以看出，在发病第60天左右(第一名病毒感染者确诊于2019年12月8日)，潜伏期人数达到峰值，之后开始骤降，而随后从第70天左右发病人数到达峰值，同时疫情得到控制，发病人数不再增长，而是开始降低，治愈人数不断上涨，与实际情况相比较为吻合。

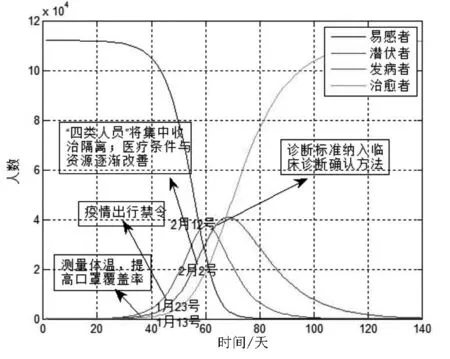
图15 政府干预下的SEIR模型拟合结果图

将SEIR模型拟合的从3月19日至3月28日的发病人数与根据确诊人数以及疑似和观察人数计算得到的发病人数进行对比，计算实际发病人数与预测发病人数的绝对相对误差，其结果为476.7，相比ARIMA模型预测的结果而言模型预测精度较低。

五、结论

从采用数据上看：ARIMA模型预测未来值需要针对某一项指标的时间序列进行预测，由于疫情中数据几乎都是短期线性变化，故所采用数据预测仅为对感染人数预测，不过ARIMA模型对于时间序列数据要求严谨，必须要平稳非白噪声序列才能使得模型具有统计意义，同时由于构建时间序列模型需要一定的数据量，故只能在传染病暴发一段时间后获得一定数据才能进行预测。而SEIR模型是对整体趋势的预测，并不对周期数据作要求，需要收集的是多项指标，是对各个指标数精确度上作要求，同时所采用数据由于是可直接获取的数值，故可根据过往传染病数据以及实时数据结合对指标数值进行调整，对于突发传染病预测能起到重要作用。

从模型构建上看：ARIMA模型是对现有序列的延续作预测，通过研究序列时间变化趋势，需要针对性地设计传染病序列的指标，需要视情况及数据来设计模型的阶值AR(p)，I(d)，MA(q)，所以不同传染病模型阶层基本不相同。而SEIR模型是通过对普遍传染病特性作预测，设计的模型算式可以适用于任何传染病数据，从易感群体、感染群体、治愈群体、潜伏群体出发，是通过模拟传染病传播模式所构建的模型，仅需要对指标数值进行替换，具有通用性，对于分析和预测传染病突发状况有重要意义。

从预测结果上看：ARIMA模型由于是对时间序列未来值的预测，所以模型本身排除了除时间以外其他因素的干扰，可以获得未来某天的预测值，同时对比现实值基本相似，故该模型预测结果较精确。SEIR模型是对整体趋势变化进行预测，由于指标计算的误差会导致模拟的传染病发展趋势与现实有略微差距，但对于整体掌控传染病疫情变化能起到重要作用，例如对拐点与峰值的预测等。