基于DSM系统检测算法的研究★

熊水平，吴 霞，周 令

（1.河池学院，广西 河池 546300；2.联想信息产品(深圳)有限公司，广东 深圳 518000）

引言

传统MIMO技术是采用多根发送天线和多根接收天线来传输信息的一种无线传输技术，此技术可以增加系统调制增益，从而降低系统误比特率及提高数据传输速率，此技术要求发射天线的个数不大于接收天线的数目个数。所以现有的多输入多输出技术得不到推广。针对现有的多输入多输出技术缺点，另一种多输入多输出即空间调制（SM,Spatial Modulation）技术被引用。空间调制SM系统首先要对无线传输信道估计，然后在接收端检测检测，但是信道估计的过程是非常复杂，并且信道估计会引起一定的误差，会导致SM系统的性能降低。针对SM系统引出了差分空间调制DSM技术，DSM技术是在空间调制SM的算法基础上，引入了针对时间域进行差分算法，信息是以空时块的形式传送，并且每个空时块包含了多个信息。而在接收端采用了一种基于M算法的检测算法D-MML（D-MML,M-algorithm to Maximum Likelihood in DSM），该算法是目前DSM系统中误比特率性能最好的检测算法，且其复杂度较低[1-4]。

1基于M算法的检测算法D-MML

1.1 D-MML检测算法

由于ML（ML Maximum Likelihood）检测算法存在着复杂度很高的缺点。因此要改进ML接收端检测算法过程，DSM系统使用M算法，得到一种基于M算法的DSM系统接收信号检测算法即D-MML检测算法。

该算法是把检测算法流程视为树状搜索结构，如图1所示，该结构包含2[log2（Nt！）]2Ntb条路径，每条路径都分别对应一个候选解信息块矩阵。当Nt=3，Nr=2，每个时隙都采用BPSK调制，M=[16，8，4，1]时的检测树状结构。图中虚候选解信息块矩阵用虚线表示，最终的检测路径用红色标记[5]。

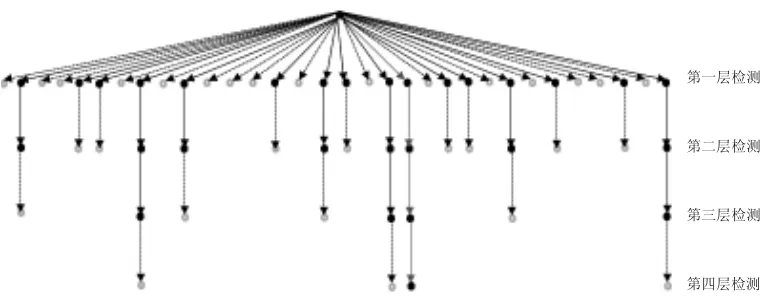
图1 D-MML检测树状结构图（M=[16，8，4，1]）

在实际应用接收端检测过程中，当前候选解信息块，其树状结构中每一层的权值可表示为：

上式中Ri-1

M表示该层候选解信息块的集合。

根据上图1可以分析基于D-MML算法的检测步骤如以下4步：

1）首先树状结构的第一层计算2[log2（Nt！）]2Ntb=32个候选解信息块的权值d1（X），X∈RM，其累计权值Dc（X）=dc（X），从32个候选解信息块的累计权值中提取16个累计权值最小的候选解信息块，得到另一个集合RM1。

2）根据树状结构的第二层，计算得到里面16个候选解信息块的第二层权值从而得到累计权值D（2X）=D（1X）+d（2X），从16个候选解信息块累计权值中提取8个累计权值最小的候选解信息块，得到另一个集合

分析D-MML算法的检测流程，在整个接收端检测系统过程中，留下树状结构的每一层的D（iX）最小的Mi个候选解信息块来进行下一层的检测，系统丢弃其它的信息块[6]。

1.2 D-MML检测算法复杂度

前面分析了D-MML算法检测流程类似树状搜索结构，可以将树状结构的检测流程分为2Nr层，所以各个序列包括2Nr个元素，其含义就是候选解信息块的数目。因此可以把ML算法的检测过程分为2Nr层，这样可以计算得到ML算法的每一层检测的复杂度为[7-8]：

然而D-MML算法各层检测的复杂度表示为如下式子：

这样可以推导出D-MML算法检测整个系统复杂度为：

根据以上式子比较D-MML算法与ML算法的复杂度，从而得到D-MML算法复杂度减少相对量如下：

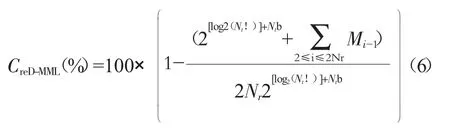
由式（6）可得到M序列的元素取值决定了算法的复杂度，M取值越小，复杂度越低。

2基于D-MML的改进检测算法D-IMML

2.1 改进的D-IMML检测算法

D-IMML算法以每棵子树为单位进行检测，检测流程如图2所示：

图2 D-IMML检测树状结构，Nt=3，Nr=2，M=[6，4，2，1]

根据图2分析可以得出D-IMML算法复杂度要低于D-MML算法达到了降低复杂度，D-IMML算法的复杂度如下式所示：

2.2动态的D-DMML检测算法

在D-MML算法的基础上引出另外一种检测算法---D-DMML算法，该算法多了一个阈值C，其与M序列一起决定了各层候选解信息块的数目，此门限值C与噪声有关，该算法如图3所示：

图3 D-DMML检测树状结构，M=[16，8，4，1]

通过分析图3可以看出D-DMML算法复杂度低于相对于D-MML算法的复杂度根据可以图3得到D-DMML算法的计算复杂度如下式所示[9-11]：

3 三种算法仿真分析

根据前面分析了DSM系统中三种改进检测算法（D-MML、D-IMML、D-DMML）过程及计算的复杂度，接下来通过仿真来验证以上三种算法复杂度，通过比较分析前面提出的三种算法的检测性能和复杂度。

3.1 检测性能仿真分析

通过蒙特卡罗仿真验证D-MML、D-IMML、D-DMM这3种检测算法性能，且以ML检测算法作为基准进行分析。且系统采用调制方式不一样得到性能不同，其仿真波形由图4所示，从图4可知，在调制方式不同的情况下，三种算法的误比特性能曲线和ML算法的误比特性能曲线都是比较接近，因此这三种低复杂度检测算法具有较好的低误比特率性能。

图4 不同调制方式下算法D-MML、D-DMML和D-IMML的误比特率，Nt=4，Nr=3

从仿真波形分析，在不同条件下，前面推出的三种改进算法性能与ML算法差不多，与公式推导一致。

3.2 复杂度仿真分析

同样分析D-MML、D-IMML、D-DMML这3种算法的相对复杂度仍然是以ML检测算法复杂度为基准，通过仿真实验得到了D-MML、D-IMML和D-DMML这3钟检测算法的复杂度波形，其波形如图5所示。

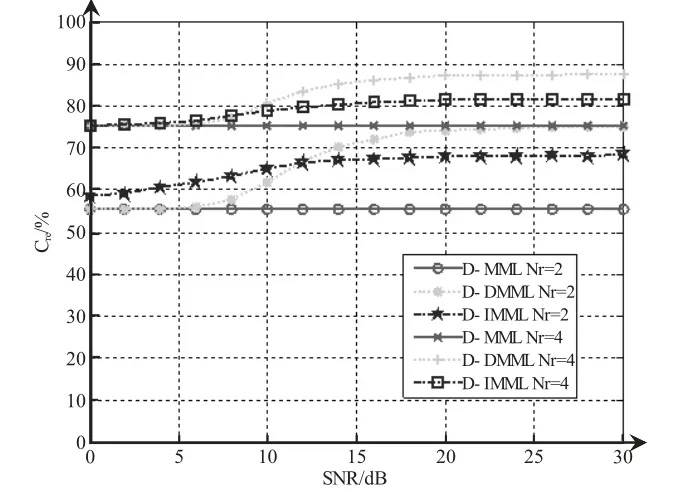
图5 Nr变化，3种改进算法复杂度，Nt=4，QPSK

图5给出了Nt=4，Nt个时隙所采用的调制方式全部是QPSK，当Nr等于2和4时，D-MML、D-IMML和D-DMML这3种算法的复杂度减少量曲线图。分析图5，这3种改进算法都能够很好地降低系统检测复杂度，同时D-IMML和D-DMML这2种算法复杂度要比D-MML算法复杂度要低。如果Nr逐渐变大，等信噪比情况下，三种改进检测算法的相对复杂度也是逐渐减少，由此可见仿真的结果与前面理论分析一致。

从图5分析可以得出前面提出的三种改进算法性能与ML算法相仿，但是其计算复杂度要比ML算法低很多。

3.3 频谱效率分析

当系统选择频谱效率都是为m=3（bits·s-1）Hz时，D-MML、D-IMML、D-DMML算法的误比特率性能是不同的。当Nt为3时，调制方式为QQ8，Nt为4时，调制方式为QQQQ，Nr为1、2、3。如下图6所示，根据以上情况分析，三种改进算法检测算法的误比特率性能仿真曲线图比较接近。在以上情况下，算法D-MML和D-DMML与ML算法的误比特率性能损失比较不会超过0.2 dB，而算法D-IMML与ML算法的误比特率性能损失不会超过0.4 dB。因此改进的空间检测算法能够保证系统的误比特率较优性能。如图6所示，当Nt所选的值及调制方式相同的情况下，误比特率性能会随着Nr的上升得到改善；当Nr不相同时，Nt=3，且调制方式为QQ8与Nt=4，调制方式为QQQQ的误比特率性能比较接近，但是在信噪比较低的情况下，QQ8比QQQQ的误比特率性能要好些，然而随着信噪比的上升，QQ8与QQQQ的误比特率性能比较接近，随着信噪比继续增加，后者的误比特率性能更好，因此性能得到进一步改善。左下方的小图形表明了Nr=2时的趋势，这两条曲线在信噪比为7时会发生重合，紧接着分开。造成这种现象的原因是，与图4、5比较分析得到在信噪比较低的情况下，不同的发射天线数会明显地影响误比特率性能，然而在信噪比非常高的情况下，不同的调制方式会明显地影响误比特率性能，同时如果接收天线数越小，那么受到发射天线数影响就越明显。

图6 频谱效率一样时，D-MML、D-DMML和D-IMML三种算法的误比特率

4 结论

本文主要研究了DSM系统关于接收端信号检测算法，目的是为了找到性能优异且计算复杂度较低的检测算法，得出了D-MML、D-IMML和D-DMML三种改进检测算法，这3种算法之间有联系，例如在D-MML算法的基础推导出来D-IMML和D-DMM这2种算法。紧接着推导了这三种算法的检测过程和理论分析了其计算复杂度，最后通过仿真分析每种算法的误比特率性能和复杂度。仿真结果证明了改进的3种算法与ML算法比较具有计算复杂度较低特性，同时其误比特率性能与ML算法相当，仿真表明了实验与理论推导结果一致。