基于用户群组的低轨卫星网络多星切换策略

朱洪涛，郭庆

（哈尔滨工业大学电子与信息工程学院，黑龙江 哈尔滨 150001）

0 引言

低地球轨道（low earth orbit，LEO）卫星星座网络具有低时延、高带宽和全球覆盖的特点，可为用户提供灵活的接入服务，成为6G移动网络的一项具有发展前景的技术[1]。近年来，OneWeb、SpaceX和Telesat 等商业公司已经开始部署具有数千甚至上万颗卫星组成的多层LEO卫星星座[2]。然而，轨道高度在350~1 200 km的LEO卫星移动速度较快，移动性导致的时延扩展、频繁切换、批量切换等问题使移动性管理成为6G 卫星通信网络的一个重要课题[3]。为了给地面用户提供连续服务，用户必须进行星间切换。由于同一位置区域附近的用户和卫星之间的通信距离和仰角非常接近[4]，导致用户发起切换的时刻也非常接近，这种切换具有并发性，大量的并发切换会导致网络拥塞，造成严重的掉话率[5]。而且用户候选切换卫星的服务时间和信道资源有较大的差异，因此并发切换的用户也要考虑多星之间的负载均衡问题。

为了给用户终端提供无缝通信服务，卫星切换策略越来越受关注。对于单一用户的切换问题，其切换策略要么基于单一标准，要么基于多个标准。目前，已有文献主要考虑3种典型的切换因素，即最大服务时间[6-7]、最大可用信道[8]和最小通信距离（也称最大仰角）[9]。文献[10]综合考虑卫星负载、用户接收信号强度和卫星服务时间等因素，提出了多属性决策的切换策略来满足用户的 QoS需求。文献[11]在静止地球轨道（geostationary earth orbit，GEO）和LEO异构卫星网络的场景中，提出了一种基于参数自适应信号与干扰加噪声比（signal to interference plus noise ratio，SINR）的多属性决策接入切换算法，综合考虑了用户的SINR、用户所需带宽、业务传输成本和卫星负载状况等因素，保证了多媒体业务的服务质量（quality of service，QoS）。近年来，一些学者引入了强化学习、博弈论和图论等方法来解决卫星切换问题。文献[12]提出了一种基于多智能体强化学习的新型卫星切换策略，将LEO卫星切换优化问题的本质归纳成一个多代理博弈问题，然后采用强化学习来降低用户的切换次数和阻塞率。文献[13]面向移动卫星网络提出了一种以用户为中心的体验质量（quality of experience，QoE）驱动的智能切换机制，采用强化学习算法，根据预测的服务时间和通信信道资源选择切换卫星，该切换机制在切换时间、切换成功率和端到端时延方面均优于传统的切换方法。文献[14]将切换过程建模为有向图，使用卷积神经网络提取不同用户的最佳切换策略的潜在规律，使得任何用户都可以根据其历史信号强度做出接近最优的切换决策。文献[15]在软件定义卫星网络架构下，将卫星切换看作一个二分图，引入了博弈论模型，当系统达到纳什均衡条件时，用户切换的成功率达到最大。文献[16]提出了一种基于网络流算法的卫星切换策略，卫星和用户之间的多重匹配可以通过计算网络流的最小成本和最大流来确定，以此确定用户的最佳切换卫星。文献[17]提出一种以用户为中心的超密集低轨卫星切换方案，利用卫星的存储能力在多颗卫星上同时缓存用户的下行数据以支持用户的无缝切换。以上的卫星切换策略均考虑单一用户的切换场景，随着低轨卫星的大规模部署，大量用户同时切换需要在卫星和控制中心之间频繁传输绑定更新消息，这将带来严重的切换信令开销，因此需要针对卫星网络特点设计新型的切换策略以降低系统的信令开销。

近年来，有一些学者开始研究多用户并发切换的问题，以降低LEO网络中用户切换的系统信令开销。文献[18]提出了一种基于用户分群的切换策略，用户上报预测的切换时刻、邻区候选集和最佳波束，卫星通过计算用户之间的相似度对用户分组进行切换，该方法能有效降低切换开销。文献[19]提出了一种用户聚类的主动切换方案，采用谱聚类算法将具有相似模式的用户分组，并将切换时间调度问题建模为非合作博弈，降低了切换阻塞率。上面两种方案[18-19]主要针对用户分组和切换时间调度展开了相关研究，文献[18]利用用户的相似度进行分组，相似度是基于用户位置计算的，文献[19]采用谱聚类的分组方法，也是根据用户的位置和运动模式来分组的。然而在多星网络中，即使同一区域位置具有相同运动模式的用户，由于其业务需求和卫星带宽资源的不同，其切换分组也会不同，因此需要面向用户业务需求和满足卫星负载限制的新型分组策略。

针对上述问题，本文提出一种基于用户群组的低轨卫星网络多星切换策略，接入卫星在考虑切换成功率、卫星吞吐率和负载均衡的条件下对用户进行分组，完成整个切换过程。

1 基于用户群组的多星切换策略

本文考虑一个具有多星覆盖的LEO卫星网络，采用分布式移动性管理方法[20]，低轨卫星网络架构如图1所示。地面被分成多个位置区（location area，LA），每个位置区有一个位置移动锚点（location mobility anchor，LMA），作为该位置区的管理中心，地面用户在同一时间可以被多颗卫星覆盖，因此当卫星进行切换时可以选择多个候选切换卫星进行切换，本文主要考虑用户的星间切换问题。

图1 低轨卫星网络架构

1.1 基于用户群组的切换流程

为了解决低轨卫星网络中大量用户并发切换造成的网络拥塞和信令开销过大的问题，本文提出了一种基于用户群组的低轨卫星网络多星切换策略。基于用户群组的低轨卫星网络多星切换信令交互流程如图2所示。大量移动用户周期性地测量当前接入卫星的信号强度，当信号强度低于切换阈值时，测量并计算候选切换卫星的集合，然后将候选切换卫星的信息发送给当前接入卫星，卫星将大量并发切换的用户进行切换分组，以群组的方式发起切换请求并更新上下文信息，可以大大减少信令的重复传输，降低大量用户并发切换的信令开销。

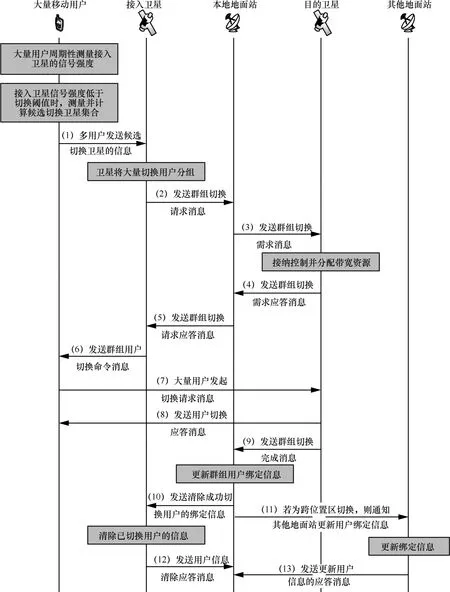
图2 基于用户群组的低轨卫星网络多星切换信令交互流程

1.2 用户群组优化算法

在上述基于用户群组的切换流程中，接入卫星对用户不同的分组方法将会直接影响整体切换性能。本文考虑特定时间段T内的卫星切换问题，卫星的集合定义为 S= {1,2,… ,N}，假定用户均匀分布在地球表面，卫星s为大量用户提供通信服务，定义在时间T内卫星s收到发起切换的用户数为Ms，其集合可以表示为 Us= {1,2,… ,Ms}，卫星s服务的用户为us,k，则其与卫星n之间的仰角定义为θs,k,n，其切换所需的带宽资源为bs,k,n，卫星与用户通信的最小仰角限制为0θ，此时卫星n可以提供的带宽资源为nB，每个卫星的最大带宽资源为Bmax，假定卫星提供的带宽和用户所需要的带宽均为最小带宽 0B的整数倍，则用户的候选切换卫星集可以表示为：

卫星与用户的仰角根据二者的地理位置信息获得，这里不做过多讨论。引入xs,k,n表示卫星s服务的用户k是否切换到卫星n，则有：因此切换过程中的带宽资源会受到以下限制：

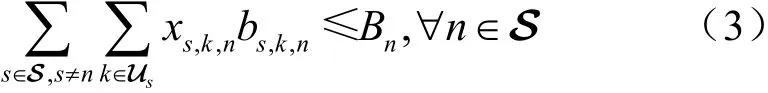
用户的分组切换可以看成一个优化问题，即每个卫星要为其服务的用户从其候选切换卫星选择一个卫星进行切换，为此定义用户的切换成功率 1G为：

由于不同用户对带宽的需求不同，在考虑切换成功率的同时也要考虑系统带宽的利用率，定义 2G为系统卫星的吞吐率，卫星吞吐率为卫星当前占用带宽与总带宽的比值，可以表示为：

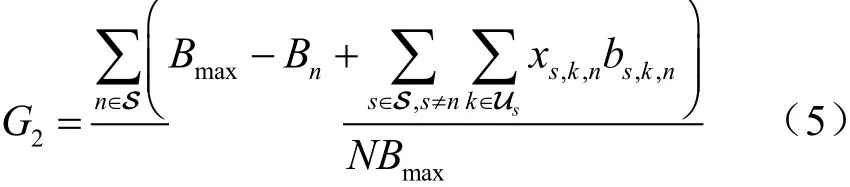
在卫星网络中，不平衡的负载会导致网络拥塞，进而降低网络的吞吐量，为此定义负载均衡增益函数为 3G，其表示为：

其中，Bvar为卫星已用带宽的方差，可以表示为：

其中，Bavg是卫星已用带宽的均值，可以由式（8）给出：通过以上分析，可以将用户的分组问题归纳为如下多目标优化问题：

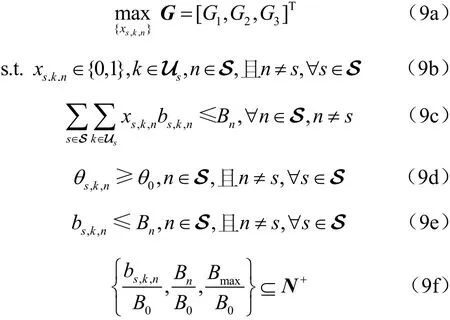
其中，N+为正整数集合。

式（9b）~式（9f）为多目标优化问题的限制条件，可以发现，寻找所有卫星服务用户的最佳切换分组是一个全局优化问题，其本质可以看作一个广义分配问题，即目标是找到每个物品到一个背包的最佳分配，其中有w个用户和v个背包，其解可以看作找到使用户切换率、卫星吞吐率和卫星负载均衡收益最高的分组方案，然而广义分配问题是NP难问题且无法在多项式时间算法内获得解决方案[21]。

考虑卫星上的计算资源有限，在一次切换时找到所有卫星负载最优的分配方法是不现实的，这里将上述问题简化。假定地面上的用户服从均匀分布，将全局优化问题转化为局部优化问题，即先考虑单颗卫星下的用户分组问题，然后再依次计算其他卫星下的用户分组，则上述全局多目

标优化问题转化成单星的多目标优化问题，具体如下：

其中，Gopt1、Gopt2、Gopt3分别由式（11）~式（14）给出：

经过上述简化，式（10a）表示的多目标优化问题本质上仍然是一个广义分配问题，即NP难问题。本文更加关注卫星切换的成功率，在保证用户切换率的同时，分组算法期望获得最大的卫星吞吐率和负载均衡收益。因此，上述多目标优化问题可以转化成3个按顺序执行的单目标优化问题，具体算法如下。

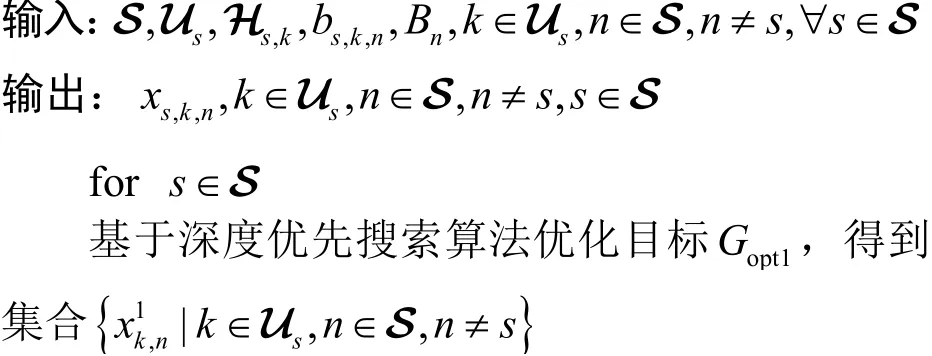
首先，地面用户将自身的测量信息上报给接入卫星，接入卫星随后将发起切换的用户按照最大切换率的优化目标进行分组，得到原始分组策略集合，然后依次根据卫星最大吞吐率和卫星负载平衡两个优化目标在原始分组策略集合中选择最优的分组策略，随后卫星按照最优分组发起群组切换请求，完成整个切换流程。

1.3 切换信令开销分析

基于用户群组的低轨卫星网络多星切换策略通过将用户进行分组，从而减少重复信令的传输，可以大大降低系统的信令开销。本文信令开销定义为信令消息大小、单位消息传输成本和消息传输跳数三者的乘积。由于卫星的移动速度远大于地面用户的移动速度，因此用户跨位置区的切换概率很小，而且本文重点关注群组切换与独立切换相比的优势，二者在跨位置区切换时，分组并不能减少绑定信息在不同位置区地面站之间更新的信令开销，因此假定用户的运动速度为0，即不发生跨位置区切换，在此条件下，提出的群组切换的信令开销可由式（15）给出：用户和卫星之间、卫星和地面站之间的信令开销；Rs为卫星s将用户划分的群组数；Hi为地面站到卫星i的跳数；HM−S为用户到接入卫星的跳数，即HM−S=1；Hs为卫星s到地面站的跳数；Hi为卫星i到地面站的跳数；α为单位消息传输成本；η为信令开销中有用数据占比。

如果用户不进行分组切换，则其开销可由式（16）给出：

对比单用户切换和群组切换的信令开销，可以发现，分组后，卫星将多个用户请求进行合并然后以群组为单位进行绑定更新，而不是单用户请求直接进行绑定更新，这样一来，可以大大减少用户绑定信息的重复传输，降低系统切换的信令开销。

2 仿真结果与分析

本文考虑多星覆盖的场景，设置卫星覆盖层数为4，即用户同一时间至少被4颗卫星所覆盖，不同层的卫星轨道夹角为45°，同一层卫星采用类地面蜂窝小区的覆盖方式，其余仿真参数见表1，在多个方面对比了传统基于最大接入信号强度的单用户切换策略和本文提出的基于用户群组的低轨卫星网络多星切换策略的性能。

表1 仿真参数设置

基于用户群组的多星切换策略最大的好处就是能够减少切换过程中的信令开销。图3为不同用户密度下系统用户切换的信令开销。与传统单用户切换相比，基于用户群组的切换策略将多个单用户的切换请求聚合为一个分组请求，以群组为单位发送绑定更新消息，而不是每个用户单独发送绑定更新消息。这样能够减少重复信令的传输，大大降低信令开销。由于卫星与地面站之间的信令开销较大，群组切换方式主要能够减少卫星和地面站之间的信令交互，因此随着用户密度增大，每个分组的用户数量增多，根据式（15）和式（16）可知，基于群组的切换策略降低信令开销的效果更为明显，仿真结果符合理论分析。

图3 不同用户密度下系统用户切换的信令开销

图4为不同用户密度下系统用户切换的成功率，对比单用户切换策略，在用户密度增加后，基于用户群组的多星切换策略的切换成功率高于单用户切换的成功率。这是因为，在用户数量较少、卫星资源充足的情况下，两种切换策略都能顺利地切换到目的卫星，但是随着用户数量增多，单用户切换策略倾向于选择满足自身需求的最佳候选切换卫星，大量用户会同时向同一目的卫星发起切换，由于卫星带宽资源有限，部分用户无法切换到目的卫星，切换成功率下降；而基于用户群组的多星切换策略会将切换成功率作为其划为群组的一个优化目标，在满足用户需求的前提下，将同一时间发起切换的大量用户划分到不同的群组并切换到不同的目的卫星，大大提高切换成功率。

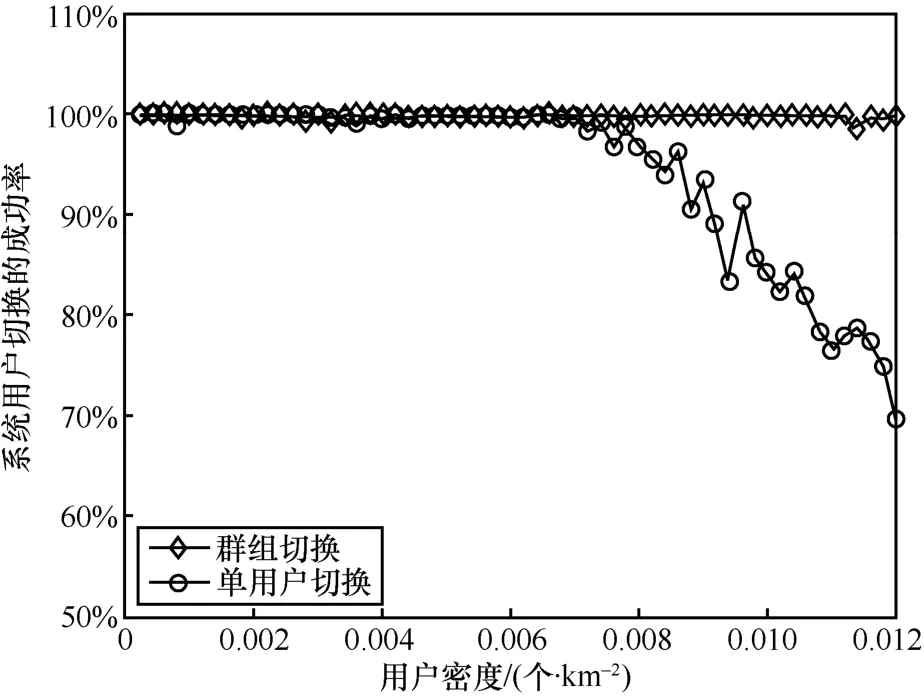
图4 不同用户密度下系统用户切换的成功率

图5为不同用户密度下系统卫星的吞吐率。基于用户群组的多星切换策略的卫星吞吐率明显高于基于单用户切换，一方面将用户划分为不同的群组，避免大量用户竞争同一目的卫星导致切换失败，进而使卫星吞吐率下降；另一方面，基于用户群组的多星切换策略会在划分群组时考虑提高卫星吞吐率这一优化目标，在切换用户数相同时，倾向于将容量需求大的用户优先分到群组进行切换，可以提高卫星吞吐率。由于用户的带宽需求不是固定的，而是在1～5 MHz的范围变化，所以随着用户密度增加，卫星的吞吐率曲线呈现出波动的情况。

图5 不同用户密度下系统卫星的吞吐率

图6为不同用户密度下系统卫星的负载均衡收益。基于用户群组的多星切换策略在平衡卫星网络负载方面有显著优势。一方面，基于用户群组的多星切换策略在将用户划分群组时将负载均衡这一因素作为其中一个优化目标，在满足切换成功率和卫星吞吐率的同时，分组策略会倾向于将用户的带宽需求尽量平均分配给不同卫星；另一方面，对比传统单一用户切换，基于用户群组的多星切换策略会将同一颗卫星的切换请求分散到不同的卫星，这两个因素都使基于用户群组的多星切换策略能有效平衡卫星网络负载。

图6 不同用户密度下的系统卫星的负载均衡收益

3 结束语

本文针对大规模低轨卫星网络中大量用户频繁进行并发切换导致的切换成功率下降及信令开销过大的问题，提出了一种基于用户群组的低轨卫星网络多星切换策略，通过将切换的用户分为不同的群组，减少了切换过程中大量绑定信息的重复传输。在此基础上，本文设计了一种基于用户群组多星切换策略的信令交互流程，并推导分析了其信令开销，同时针对如何分组这一问题，考虑了用户切换成功率、卫星吞吐率和负载均衡3个主要因素，将用户分组问题转化成多目标优化问题并设计了优化分组算法。仿真结果表明，与传统单用户切换策略相比，所提出的基于用户群组的多星切换策略能够有效降低网络的信令开销，同时在提高切换成功率、提高卫星吞吐率和平衡网络负载方面也有显著的优势。在未来的研究中，可以考虑加入卫星对用户行为的预测，结合卫星自身的星历信息对资源进行预分配以更好提升切换性能。