基于移动边缘计算的任务卸载策略
2022-05-06张晓龙吴巍周彬
张晓龙, 吴巍, 周彬
(1.中国电子科技集团公司第五十四研究所, 石家庄 050002; 2.中国电科电子科学研究院, 北京 100041)
作为一种新的计算模式的移动云计算(mobile cloud computing,MCC),将移动设备的计算任务部分或全部放在附近云计算上进行,降低移动设备能耗并提高其计算能力[1]。移动边缘计算(mobile edge computing,MEC)作为5G网络的基础,彻底改变传统云模式,拓展了移动云的范围[2]。然而,由于MEC有限的计算资源和复杂的网络环境,资源分配和负载不平衡等问题是制约MEC可扩展性和网络性能的关键因素。因此,对任务卸载策略进行研究具有重要的实际意义。
到2021年,中外研究人员对移动边缘计算的任务卸载策略进行了大量的研究,从多方面提出了一些可能的解决方案,并取得了一些优秀的成果。如盛津芳等[3]将改进拍卖算法用于移动边缘计算的任务卸载,主要由两个部分组成:卸载和调度。结果表明,该策略在一定程度上降低了设备能耗合服务时延,用户满足度较高。路静等[4]提出了一种移动边缘计算分割和最优卸载策略,以联合优化系统的3个目标(即能量、延迟和公平性)来构建模型,并对其进行求解。结果表明,所提出的卸载和调度策略能有效地提高系统性能。高寒等[5]将深度神经网络用于移动边缘计算的任务卸载,以最小延迟和最低能耗为目标建立评价模型。结果表明,相比于传统的卸载策略,该策略综合考虑时延和能耗,综合最优。齐平等[6]将信任模型用于移动边缘计算的任务卸载,结果表明,该方法以一定的时间开销为代价,可以有效地提高应任务执行成功率。但是,在MEC服务器的计算资源受到限制的情况下,大多数研究都未对其进行考虑,无法进一步降低时延和能耗,适应性有待进一步提高。
在此基础上,提出了一种结合通信时延和计算时延的优化卸载策略用于移动边缘计算网络。该策略根据设备的计算能力和链路的传输速率不同,对移动用户任务进行决策。通过仿真验证了该方法的优越性。
1 移动边缘计算网络框架
在MEC网络结构中,计算和存储容量被下放到移动网络的边缘,如基站和无线接入点[7]。移动设备可以将应用任务卸载到附近的MEC计算节点进行处理,进行低时延的计算服务。图1所示为5G移动网络的基本MEC框架。它由核心网、边缘云和移动设备组成。

图1 移动边缘计算框架Fig.1 Mobile edge computing framework
(1)核心网络。在MEC网络体系结构中,其核心网络的功能与传统MCC网络体系结构相同。MEC服务器的各种资源明显少于核心网。因此,如果MEC服务器不能处理移动设备的任务请求,它将请求核心网进行处理。此外,核心网还负责存储大量的数据信息、数据集成、分析和全局数据共享等[8]。
(2)边缘云。边缘云主要由各种MEC服务器组成,在网络边缘部署计算、存储等资源。与传统的MCC网络架构不同,计算和存储等资源的部署更接近移动设备。因此,通过将任务卸载到边缘云(或MEC服务器)进行本地化处理,移动设备可以有效减少任务处理延迟,节省设备能耗。在MEC网络体系结构中,MEC服务器的主要功能是处理移动设备的卸载任务,满足移动设备对低时延、可靠性和位置感知的需求。
(3)移动设备。移动设备主要是指处于网络边缘的用户使用的各种设备,包括智能手机、可穿戴智能设备、笔记本电脑和无人驾驶汽车等。在MEC网络体系结构中,移动设备是各种应用任务处理的发起者,是MEC计算服务的主要用户。
2 卸载策略
为了解决移动边缘计算网络中任务是否迁移和迁移到哪里的问题,降低系统时延,提出一种结合通信时延和计算时延优化策略用于移动边缘计算网络。
2.1 计算时延和通信时延分析
在实际环境中,附近的很多MEC都满足传输要求。但是,想要短时间内完成任务处理,就需要对计算和通信时延进行考虑。
(1) 计算延迟。计算延迟包括由计算任务量xkij在MECj中引起的时延和本地设备中处理的任务量Wk-xkij引起的时延[9]。在MECj中产生的时延计算公式为
(1)
式(1)中:k为移动用户编号;i为用户k任务传输的MEC;j为处理xkij任务的MEC;Pj为MECj计算速率。
以MEC的最小计算时延作为目标,表达式[10]为
(2)
本地计算时延公式为
(3)
式(3)中:l为本地设备编号;Pkl为移动用户k本地设备的计算速率。
因此,任务量xkij计算时延公式为
(4)
(2)通信时延。移动用户k将任务xkij卸载到MECi上的延迟计算式[11]为
(5)
则移动用户的上、下行传输速度表达式为
(6)
(7)


前者的通信时延可由式(5)计算,后者的通信时延计算式[12]为
(8)
(9)

因此,任务量xkij的通信时延计算式[13]为
(10)

(11)
综上所述,系统平均最小时延表达式为
(12)

系统的平均最小延迟约束有两个条件。
(1)移动用户卸载的任务量不应大于总任务量,即
0≤xkij≤Wk,k=1,2,…,K;i∈I;j∈J
(13)
式(13)中:Wk为用户k需要计算的密集型任务。
(2) 此任务在MECj种计算的任务量小于或等于MECj计算资源的最大量Cj,表达式[15]为
(14)
式(14)中:Cj为每个MEC的最大计算资源。
2.2 时延联合优化算法设计
在MEC网络场景中,卸载和计算都存在一定的时延。提出了一种结合通信时延和计算时延用的联合优化卸载策略用于移动边缘计算网络。该策略通过移动边缘计算设备不同的计算能力和通信链路的不同传输速率,对移动用户任务进行决策,最小化系统时延。算法步骤如下。
步骤1:对于每个用户k,找到可通信的MEC集合I,在参考文献[16]计算得到信噪比SINRs和信噪比阈值SINRmin。如果SINRs≥SINRmin,可以与用户通信并转移任务,将符合条件的MEC放入集合I中,不符合条件的放弃。根据计算资源Cj与其阈值Cmin,进一步对MEC进行判断,得到能够对任务进行处理的MEC集合J。
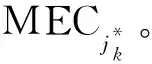



图2 算法流程Fig.2 Algorithm flow
3 仿真结果与分析
3.1 仿真参数
为了对文中方法的性能进行验证,通过仿真分析该方法对任务大小和时延的影响。仿真设备为联想PC机,操作系统为windows 10 64位旗舰,Intel i52450 m CPU,频率2.5 GHz,8 GB内存,MATLAB r2018a为仿真平台[17]。MEC参数见表1。
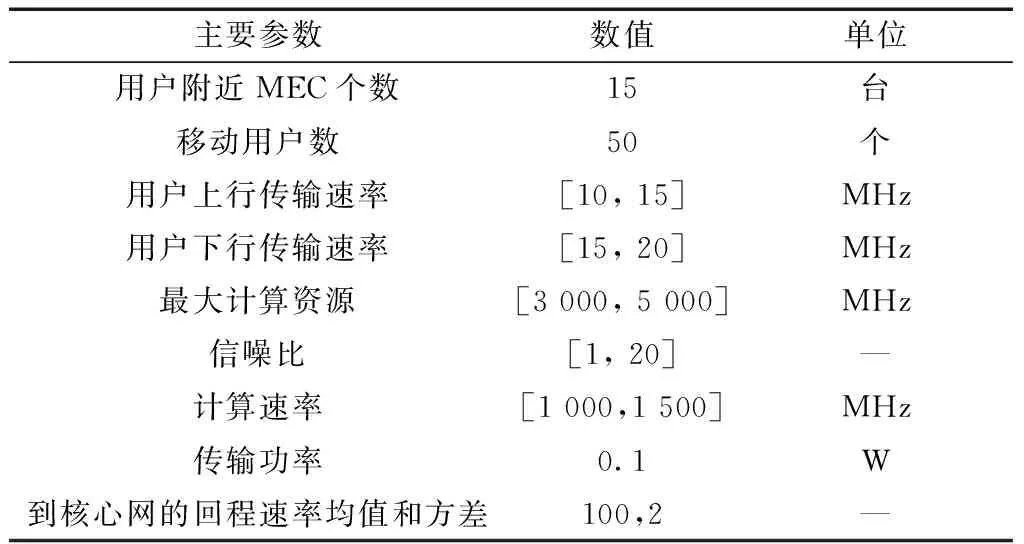
表1 MEC参数表Table 1 MEC parameter table
3.2 仿真分析
3.2.1 不同算法的性能比较
文中提出的算法与文献[18]中提出的SMT算法和文献[19]中提出的PSwH算法进行了比较。图3所示为平均时延随任务量增加的延变化曲线,任务量为100~400 Mbits,各用户任务量相同。
从图3可以看出,平均卸载时延随着Wk的增加而增加。相比于SMT算法和PSwH算法,文中算法的平均时延增长最为缓慢。这是因为SMT算法选择的MEC是时延最低的,但不考虑MEC的计算和通信能力。换言之,有些MEC计算能力强,但传输速度慢,或者MEC传输速度快,但计算能力弱。PSwH算法选择传输时延较小的MEC,但是MEC的计算能力可能不如其他MEC,并且MEC产生的计算时延也不是最低的。

图3 平均时延随任务数变化曲线Fig.3 Variation curve of average delay with number of tasks
图4所示平均时延随用户数K增加的变化曲线。用户数从30到150,此外,将任务量设置为Wk=200 Mbits。
从图4可以看出,平均卸载时延迟随着用户数量的增加而缓慢增加。这是因为符合要求的MEC有多个,因此即使用户数量增加,对传输和MEC计算无明显影响。此外,与其他两种算法相比,文中算法具有最小的平均时延。这是因为文中算法考虑计算能力和通信能力所致。
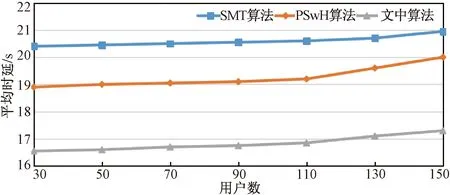
图4 平均时延随用户数变化曲线Fig.4 Curve of average delay with the number of users
图5所示用户迁移概率随MEC增加的变化曲线。MEC数量为10~50。此外,将任务量设置为Wk=200 Mbits。

图5 迁移率随MEC数量的变化曲线Fig.5 Curve of mobility with the number of MECs
从图5可以看出,PSwH 算法的迁移概率不断MEC数量变化而变化,这是因为PSwH 算法仅考虑通信时延最小化。对于SMT算法,迁移概率通常在50%左右,这是因为SMT算法仅考虑时延阈值,而延迟阈值与MEC数目无关。因此,迁移概率基本保持不变。MEC数量40是文中算法的分界点,小于40时,迁移概率逐渐增加,这是因为MEC增加可选择性越大。当MEC个数超过40个时,迁移概率逐渐稳定在1,此时不管MEC怎么增加,用户必须迁移。
3.2.2 时延分析
式中:表示试验点x落入估计的可行域的概率(可行性概率),记作和表示第i个约束函数Kriging模型的预测均值和标准差。CEI准则概念简单、计算容易,但该准则受PoF的影响大,收敛到可行域边界上最优解的效率不高。基于CEI准则的代理优化算法在本文简称CEI算法。
通过仿真实验比较了该算法在通信时延、计算时延和系统时延方面的性能。图6所示三种时延随任务量增加的变化曲线。任务量为100~400 Mbits,各用户任务量相同。
从图6可以看出,所有3个平均延迟都随着任务量Wk的增加而增加。然而,计算时延明显小于通信时延。另外,随着任务量Wk的增加,增长相对缓慢。这是因为用户计算密集型度高且有卸载MEC,那么大部分延迟都是由传输任务导致的。相比于用户设备,MEC的计算能力较强,对多个任务进行处理仅需极短的时间。此时,MEC产生的计算延迟较小。
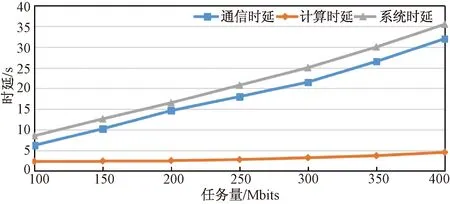
图6 3种时延随任务量的变化曲线Fig.6 Three kinds of delay curves with task volume
图7所示为3种计算时延着任务量增加的变化曲线。任务量为100~400 Mbits,各用户任务量相同。
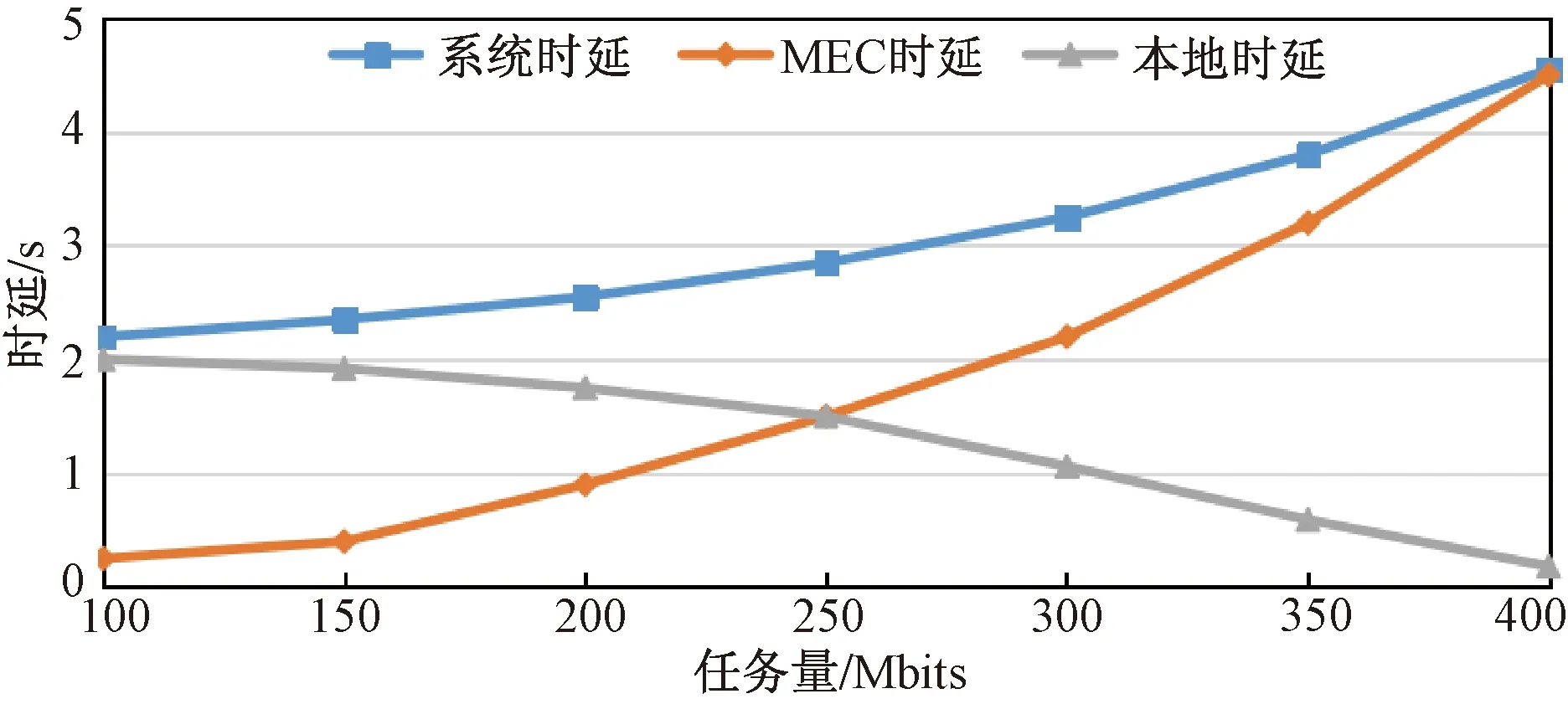
图7 计算时延随任务量的变化曲线Fig.7 Calculate the variation curve of delay with task volume
从图7可以看出,3种计算时延在任务量超过250 Mbits后本地计算最优,任务量为0~250 Mbits时MEC计算最优。这是因为任务量较少时,可以由用户自身对任务进行处理,降低了通信时延。随着任务量Wk的增加,一定程度上限制了用户计算能力,在处理大任务时会出现较大的计算延迟。因此,该算法将一些任务转移给MEC,并以较小的计算时延代价交换通信时延代价。
图8所示为3种平均时延随用户数增加的变化曲线。用户数为30~150,此外,将任务量设置为Wk=200 Mbits。
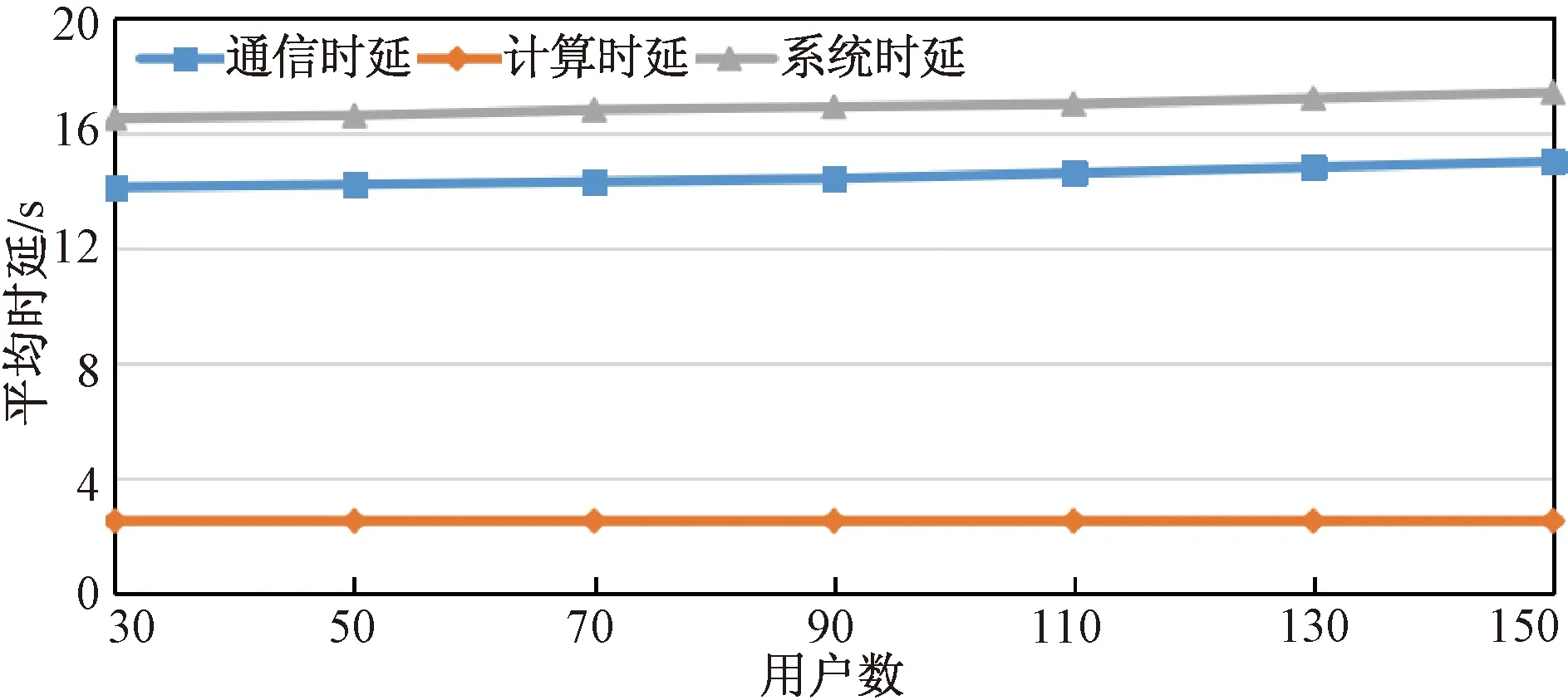
图8 3种时延随任务量的变化曲线Fig.8 Three kinds of delay curves with task volume
从图8可以看出,平均卸载时延随用户数增加增速较为缓慢。与前面类似,计算延迟远小于通信延迟。而随着任务量Wk的增加,增长相对缓慢。
4 结论
移动边缘计算可以为各种应用提供低延迟、高可靠的移动服务。在5G移动边缘计算中,合理有效的任务调度策略是保证应用服务质量和提高系统性能的关键。因此,文中综合考虑通信和计算时延,设计了一种实用高效的卸载策略。主要结论如下。
(1)在移动边缘计算网络中采用结合通信时延和计算时延的卸载策略,通过移动边缘计算设备不同的计算能力和通信链路的不同传输速度对移动用户的任务进行决策,该研究具有一定的实用价值。
(2)仿真结果表明,该方法能显著降低平均卸载时延。随着任务数的增加,文中方法的时延增长最慢,说明文中方法具有一定的实用性。
文中主要研究了任务卸载策略。从目前的实验设备和数据规模来看,文中研究还处于起步阶段。基于此,逐步完善卸载策略将是下一步工作的重点
