合作博弈视角下慕课联盟利益分配机制设计

赵佳莹， 俞颂华

(宁波幼儿师范高等专科学校 阳明人文学院， 浙江 宁波 315336)

当前，优质教育资源供需不平衡仍是教育发展的主要矛盾。针对该问题，宁波市教育局出台《宁波市教育信息化三年行动计划(2020—2022)》(以下简称《行动计划》)，提出2022年底，扩展数字资源，丰富供给方式，满足优质资源需求。尽管当今快速发展的互联网和信息技术为解决这一矛盾提供了有效途径，但各校参与教育资源建设的积极性仍较低，且教育资源质量参差不齐。对此，《行动计划》提出宁波将建立健全教育资源建设的合作机制。

宁波高校慕课联盟是由宁波市教育局和宁波市数字图书馆联席会议支持，在甬高校共同发起成立的，旨在推动在甬高校慕课建设和教学改革，建立区域内高校共建共享优质教学的合作机制。利益分配机制是各高校参与共建共享优质资源的内在动力[1]。因此以宁波高校慕课联盟平台为例，针对平台与高校、高校与高校间的两大利益分配问题，设计利益分配机制，促进各高校共建共享优质慕课，扩展宁波市优质数字教育资源。

1 文献综述

关于利益分配机制的研究中，一部分学者采用委托代理模型。该模型由美国经济学家伯利和米恩提出，是契约设计的主要内容[2]。Fish等[3]、Spence和Zeckhauser[4]、Ross[5]提出运用委托代理模型设计委托人与代理人之间的利益分配机制，以此提高参与主体的积极性。李恩极等[6]运用委托代理理论设计了政府主导下产学研协同创新的利益分配机制，对企业和科研机构发挥了有效的激励作用。在慕课联盟平台上，平台是核心主体，高校是参与主体，平台为了获得更高的经济利益可能减少对高校群体的奖金分配，降低高校参与建设优质教育资源的积极性，针对该问题可通过委托代理理论设计慕课联盟平台与高校之间的利益分配机制。

关于利益分配机制，部分学者采用Shapley值模型。陈海贝[7]从知识共享、政策共享、技术共享和风险承担4个维度考虑合作方(包括高校智库、企业和政府)的贡献程度，利用Shapley值法构建了高校智库联盟的利益分配机制模型，该模型体现了多劳多得、不劳不得的分配原则。孙耀吾等[8]基于参与主体特征及合作利益分类，构建修正后的Shapley值二阶段模型，分析高技术服务创新网络的利益分配机理。余建军等[9]在经典Shapley算法的基础上，建立包含投入成本价值、风险分摊系数等因素在内的Shapley修正模型，探讨爆仓情况下电商物流企业联盟的利益分配问题。刘枬等[10]基于参与方资源投入和风险分担两个因素构建修正后的Shapley模型，解决合作参与方的超额利益分配问题。以上研究均基于合作方利益的影响因素构建Shapley值修正模型，使得利益分配公平合理，该模型可以解决慕课联盟平台上高校之间的利益分配问题。

除此之外，也有学者同时运用委托代理理论与Shapley值法研究利益分配机制。张瑜等[11]以产业技术创新战略联盟为例，将根据Shapley值法求出的核心主体对参与主体的奖励支付融入利益协调的契约设计中，优化产业技术创新战略联盟产学研网络型合作利益分配的契约设计，减少参与主体的道德风险问题。张忠寿等[12]基于科技金融生态系统中协同创新的利益分配问题，分别应用委托代理理论和改进Shapley法构建2个利益分配模型，研究发现该方法既可以体现依据收益高低进行利益分配的原则，也可以实现公平与效率兼顾。以上研究均止于提出利用利益契约的方式激励参与者提高努力水平，但是忽略了联盟主体作为“经济人”的角色，如何在公平公正、多劳多得的利益分配原则下，实现联盟主体的收益最大化是亟待解决的问题。

因此，以宁波高校慕课联盟平台为例，利用Shapley值改进模型设计高校间的利益分配方式，并将其融入慕课联盟平台与高校的利益分配契约中，设计在公平合理的利益分配原则下实现平台利益最大化的机制，激励慕课联盟平台和高校共同推动优质数字教育资源建设的发展。

2 模型构建与分析

2.1 慕课联盟平台与高校间利益分配的委托代理模型构建

宁波高校慕课联盟平台在与各高校合作过程中，平台为了获取更大的利益，减少对高校群体的奖金分配额度，降低高校加入慕课联盟的积极性，影响平台向公众推出优质教育资源。对此，构建平台与高校间的委托代理关系，研究合作中的利益协调问题。

假设目前共有n所高校，高校i的行动分别为加入慕课联盟和不加入慕课联盟，i∈[1,n]。平台为了激励高校均加入慕课联盟，共建优质教育资源，对联盟在不同数量规模下制定不同的奖金分配比例。当只有1所高校加入时，设置q1的奖励分配比例，当2所高校加入时，设置q2的奖励分配比例，当n所高校均加入时，设置qn的奖励分配比例，其中qn∈(0，1)。

根据上述假设，当所有高校均加入联盟时，平台的期望收益为

(1-qn)v1…n

(1)

式中，v1…n表示n所高校均加入联盟后给平台带来的总价值，如公共利益、社会价值和经济利益[13]。同理高校1和高校2加入联盟后给平台带来的价值记为v12，高校2和高校3加入联盟后给平台带来的价值记为v23，其他组合形式以此类推。

为了促使高校加入联盟，则需要满足参与约束条件，即加入联盟的收益大于不加入联盟的收益，即

(2)

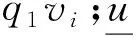
为了鼓励已经加入联盟的高校进一步带动兄弟院校加入，扩大联盟的数量规模，此时需要满足激励相容约束条件，即n所高校均加入联盟后各自分配获得的收益大于高校独自加入联盟获得的收益，即

ui>q1vi

(3)

式中，ui表示n所高校均加入慕课联盟后各自分配得到的收益，该收益可在平台划拨的奖金额度(即qnv1…n)中进一步利用Shapley值模型分配获得。

由于慕课联盟合作中各高校是利益风险共担者，因此设高校是风险中性，此时平台和高校之间的利益分配模型为

(4)

2.2 高校与高校间的利益分配模型构建

确定高校群体获得的奖金额度后，如何进一步合理分配高校之间的奖金，是激发高校建设优质教育资源的关键。由于每所高校的能力差异，对建设慕课投入的努力水平和资源不同，导致高校在联盟平台上对建设慕课的贡献度也不同。若所有高校最终获得的奖金额度均相同，高贡献的高校将退出联盟平台。因此有必要建立高校与高校间的利益分配机制，帮助联盟平台长效运营发展。

2.2.1 原始Shapley模型

Shapley值法是博弈论中解决多人合作博弈成本分摊或利益分配的方法，即通过考虑联盟成员对联盟的边际贡献将利益或成本进行合理分配[14]。对Shapley值模型可具体描述为：在一个大联盟I中，由n个成员组成的联盟集合，I={1,n}。当联盟中单个成员工作时，获得的收益为vi；当联盟成员组成联盟时，联盟的总收益为uI,每个联盟成员分得的利益为ui。除此之外，运用Shapley值法进行利益分配还应该满足以下条件：

(5)

(6)

ui≥vi(i∈I)

(7)

假设S是联盟I的一个子集，即S∈I。|S|表示子联盟中成员i的个数，vS表示子联盟S的收益，联盟S中除去成员i的收益可表示为v(Si),w(i)表示权重系数，则每个成员在联盟中分得的收益可表示为

vi=∑i∈S∈I(w|S|)[vS-v(Si)](i∈I)

(8)

(9)

2.2.2 改进Shapley模型

以上Shapley值法在运用过程中存在一个重要假设——对称性，即任何人对联盟的边际贡献都相同。传统方法忽略了个体的差异性，因此需要做出改进。通过改进Shapley模型，使得慕课联盟平台可以根据各校在建设优质教育资源方面的贡献度合理分配奖金。

1)确定2个关键因素各自的评定值。假设评定高校加入慕课联盟后的贡献度，取决于他们建设慕课的数量和质量，令a1为慕课的数量，a2为慕课的质量。慕课数量a1可以直接观测到，慕课质量a2可以通过专家评定和用户対慕课的好评率综合得出。

2)确定2个关键因素的权重。假设慕课数量和慕课质量的权重分别为wa1和wa2,wa1+wa2=1且每个权重值都为正值。

3)确定奖金分配优化值。当联盟平台上有n个高校时，高校i收获奖金后的收益函数为

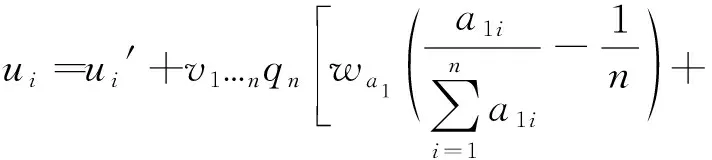
(10)

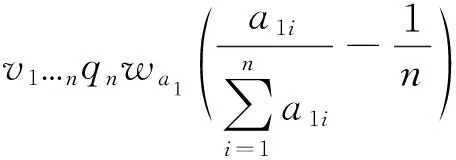
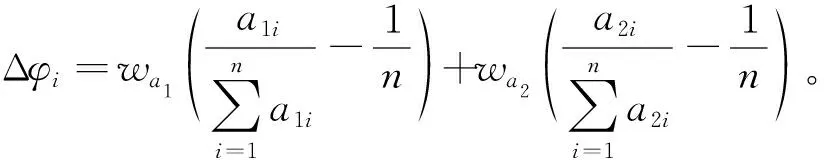
结论1：高校获得的奖金分配比例受其自身在慕课数量和质量两方面贡献度的影响。当自身的贡献度小于其他高校的平均贡献度时，那么就需要从自身的收益中划分出一部分给予其他高校作为补偿，获得的收益减少；反之当自身的贡献度超过其他高校的平均贡献度时，将收到其他高校给予的补偿，获得的收益增加。高校为了获得更高的收益分配，会在慕课数量和质量两方面付出更高的努力，争取贡献度超过其他高校。可见该分配方式体现多劳多得、公平公正。

2.3 基于委托代理模型和Shapley值改进模型的利益协调

在式(4)慕课联盟平台与高校的利益分配方式下，将根据Shapley值改进模型得出的高校间利益分配值式(10)代入式(4)中，旨在进一步设计既能满足公平合理的利益分配原则，又能实现平台利益最大化的机制，激励慕课联盟平台和高校共同推动优质数字教育资源建设的发展，具体为

(11)

为了方便分析，假设有2所高校加入联盟，即当n=2时，已知q1，式(11)可表示为

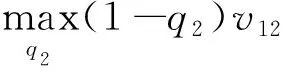
(12)

解得

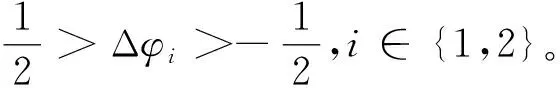
假设有3所高校加入联盟，即当n=3时，已知q1和minq2，式(11)可表示为

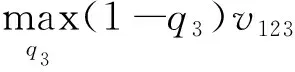
(13)

解得

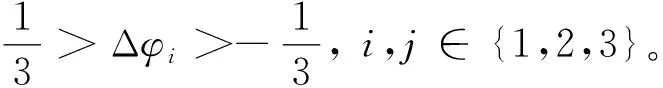
g(i)=

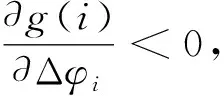
结论2：慕课联盟平台为了激励更多的高校加入联盟，共建优质教育资源，可在联盟的不同数量规模下设置不同奖金分配比例，且在设置时应当兼顾联盟中贡献度最低的高校，保证其获得的分配收益大于其独自加入联盟时的收益。在该条件下，不仅能扩大联盟的数量规模，还能最大化平台的收益。

3 算例分析

假设共有3所高校，分别为高校1、高校2和高校3。当只有高校1加入慕课联盟平台时，可创造的价值v1=100。只有高校2加入慕课联盟平台时，可创造的价值v2=120。只有高校3加入慕课联盟平台时，可创造的价值v3=130。当高校1和高校2均加入慕课联盟平台时，可创造的价值v12=240，高校1和高校3均加入慕课联盟平台时，可创造的价值v13=250，高校2和高校3均加入慕课联盟平台时，可创造的价值v23=280。3所高校均加入慕课联盟平台时，可创造的价值v123=440。

3.1 初始利益分配

根据Shapley值法，可计算出高校1、高校2和高校3初始利益分配值(表1～表3)。

3.2 改进后的利益分配

假设慕课联盟平台在利益分配中考虑指标慕课数量和慕课质量被量化分别为a1=(2,2,3),a2=(4.5,4.7,4.8)。

设置评定慕课数量的权重wa1(S)=0.4，慕课质量的权重wa2(S)=0.6。此时可得出3个高校的利益变量v123q3Δφi(u)分别为

v123q3Δφ1(u)≈-11.44q3

(14)

v123q3Δφ2(u)≈-7.48q3

(15)

v123q3Δφ3(u)≈18.92q3

(16)

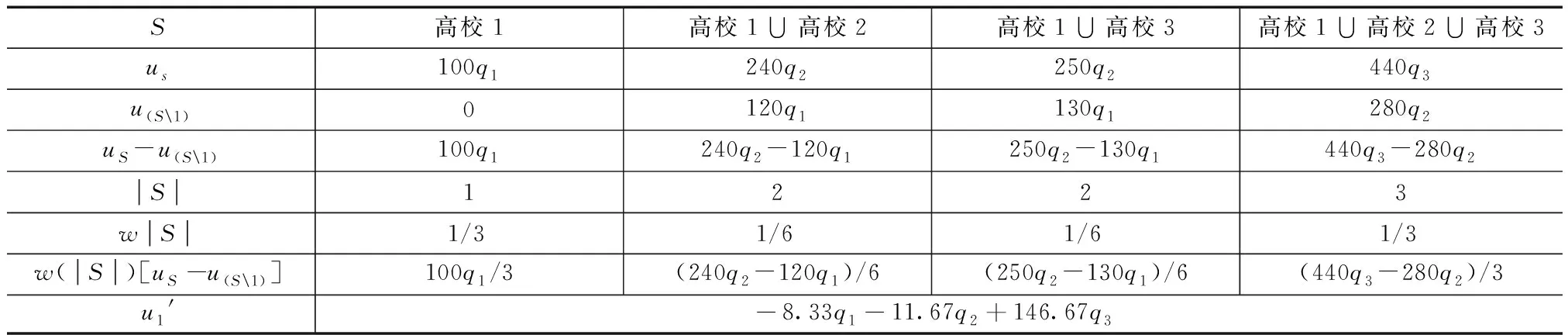
表1 高校1初始利益分配表

表2 高校2初始利益分配表

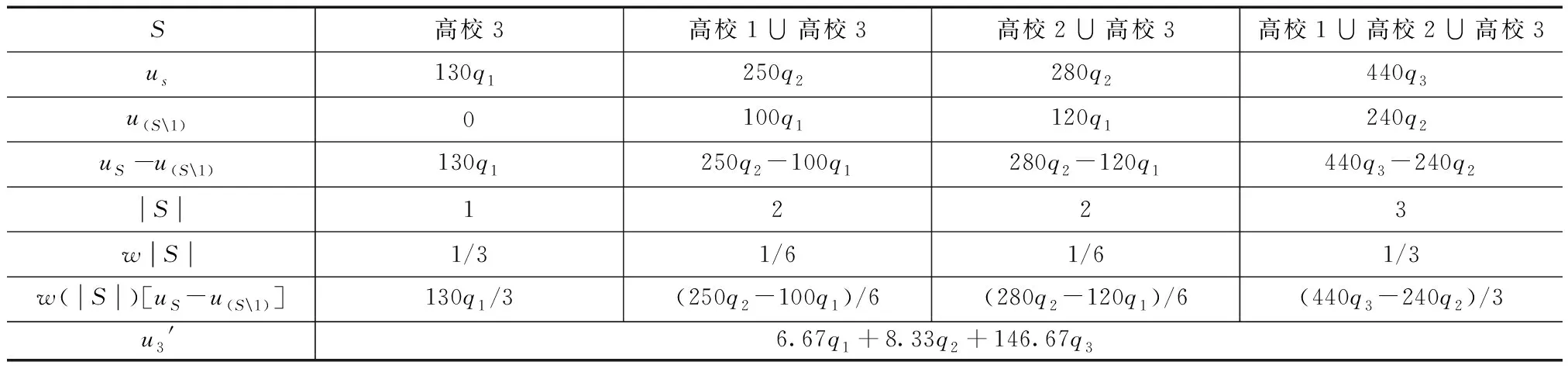
表3 高校3初始利益分配表

最终可得3个高校的收益分配分别为

u1=u1′+v123q3Δφ1(u)=-8.33q1- 11.67q2+135.23q3

(17)

u2=u2′+v123q3Δφ2(u)=1.67q1+ 3.33q2+139.19q3

(18)

u3=u3′+v123q3Δφ3(u)=6.67q1+ 8.33q2+165.59q3

(19)

将改进后的利益分配与初始利益分配相比较，发现贡献度最高的高校3获得收益分配相比于初始增加了，且增加的值恰好等于贡献度较低的高校1和高校2减少的利益分配值。验证了Shapley值改进模型的合理性，满足多劳多得的公平分配原则。

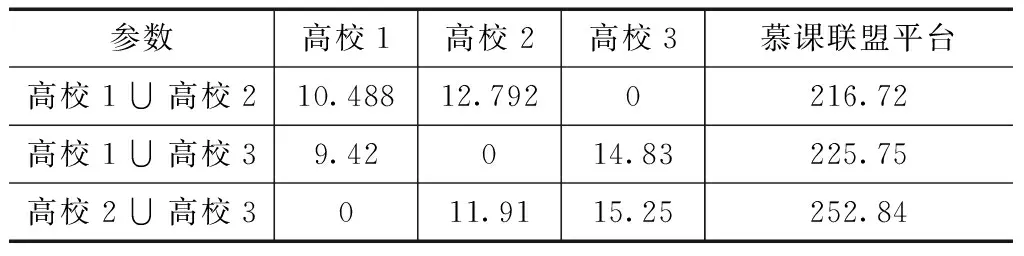
表4 当q2=0.097时，不同组合形式下各主体的收益

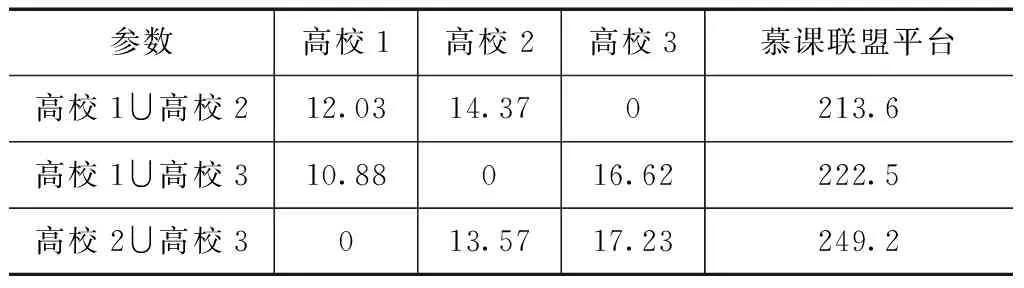
表5 当q2=0.11时，不同组合形式下各主体的收益

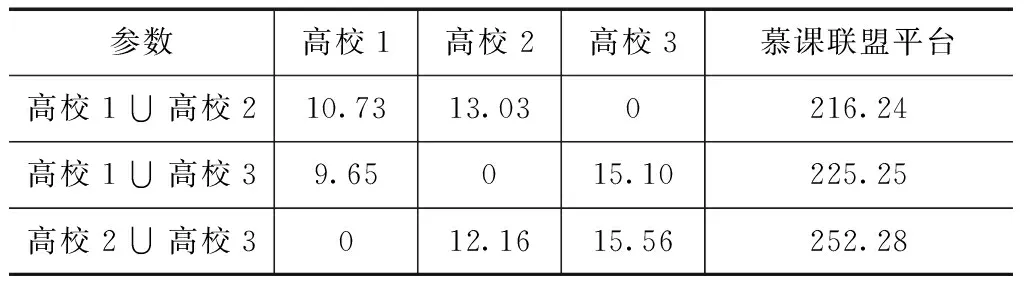
表6 当q2=0.099时，不同组合形式下各主体的收益

根据上述分析，只有当q2=0.11时，各校以不同组合形式加入联盟后获得的收益均大于其独自加入联盟时的收益。同时对比在联盟的不同数量规模下，发现2所高校加入时联盟平台的收益大于只有1所高校加入时的收益。

同理当3所高校均加入联盟时，在q1=0.1，q2=0.11的前提下，根据条件

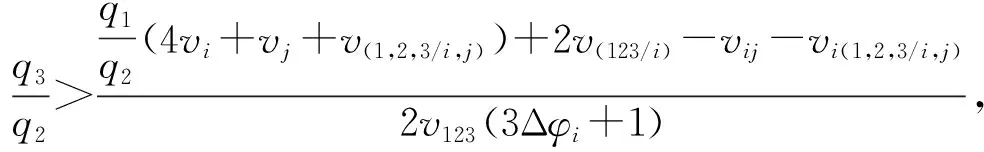
根据表7可得出，当q3=0.09时，所有高校的收益分配均大于其独自加入联盟时的收益，此时有利于扩大联盟的数量规模。对比在联盟的不同数量规模下，发现3所高校加入时联盟平台的收益大于只有2所高校加入时的收益。

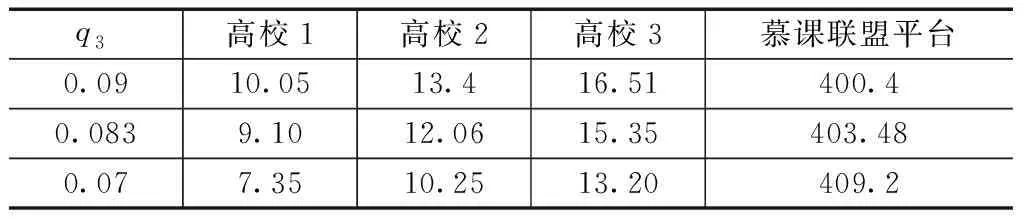
表7 不同奖金分配比例下各高校的收益

因此慕课联盟平台需要在联盟的不同数量规模下设置不同的奖金分配比例，且设置的奖金分配比例使得建课贡献度最低的高校获得的收益分配大于其独自加入联盟时的收益，有利于扩大联盟的数量规模，提高平台的收益。

4 结论与展望

数字化时代下，为丰富优质数字教育资源，慕课联盟平台日益频繁。面对平台运营中高校参与积极性低、教育资源质量参差不齐的问题，合理的利益分配机制成为平台发展的重要保障。根据利益分配的主体不同，可将机制分为如下两个部分：

1)慕课联盟平台与高校间的利益分配。运用委托代理理论构建慕课联盟平台与高校间的委托代理模型，并将其与高校间的Shapley值改进模型融合，在联盟的不同数量规模下设置不同的奖金分配比例，以利益契约的方式让高校自主选择是否加入慕课联盟平台。研究得出平台在设置奖金分配比例时需要结合各校建课的贡献度差距，即兼顾建课贡献度最低的高校，使其在联盟数量规模增大的过程中，获得的收益始终大于其独自加入联盟时的收益，此时有利于扩大联盟的数量规模，提高联盟平台的收益。

2)高校与高校间的利益分配。引入慕课数量和慕课质量两个指标，将其赋予权重并与Shapley模型结合，得到Shapley值改进模型。研究得出在一定的奖金分配额度下，各高校间的利益分配将以在慕课数量和质量上的贡献度为依据。贡献度越大的高校，获得的收益将越多。反之贡献度越小的高校，将从自身的收益中划出一部分用来弥补贡献度高的高校，获得的收益将越少。该机制恰好体现多劳多得的公平分配原则。

通过上述研究，在联盟平台为“经济人”角色下，验证了合理的“让利”方式有利于实现利益分配的激励目的[15]，同时对现有关于联盟平台利益分配的方式做了补充。研究存在的不足之处是，扩大联盟平台规模适合在初始导入阶段，随着平台的成长、成熟，势必需要进一步提高其综合水平，才能给平台带来规模效应。因此在未来的研究中，需要结合联盟平台的发展阶段来设计机制，促进慕课联盟平台的发展。