多机场区域内机场与航司战略合作模式研究
2022-05-06时晓盼
朱 佳, 时晓盼, 韩 敏
(中国民用航空飞行学院 经济与管理学院, 四川 广汉 618307)
机场完善了城市之间的交通运输网络,对区域经济的发展有着重要的推动作用。以广州白云机场和深圳宝安机场为例,白云机场和宝安机场货运量的增加带动了广州和深圳的第三产业发展[1]。不仅大机场可以带动经济增长,中小型机场也是偏远地区必要的基础设施,有利于促进地方旅客流动[2],从而在带动城市经济增长方面发挥不可替代的作用[1]。由于机场的正外部性,中国各地区政府都十分注重机场的建设与发展。截至2016年底,中国三千万级机场达到10个,千万级机场达到28个。随着机场数量的快速增长,区域内部机场分布的密度越来越高。邻近机场之间的关联愈发紧密,大型机场之间以及大型机场和小型机场之间均有着越来越强的竞争与合作,这种多个机场共同服务同一片区域的现象被称为“multi-airport system”,即区域多机场系统,也称为机场群[3]。
然而,在多机场区域内,机场间的发展并不均衡。民航局发布的2019年生产量统计公报显示,2019年,中国境内运输机场共有238个,其中中小机场有165个,占机场总数的69.3%,中小机场在中国民航运输系统中所占比重很大,但其旅客吞吐量只占全国总量的6.8%,且绝大部分地处经济不发达地区。部分机场从报表反映来看仍然亏损严重,生存和发展面临着严峻挑战。随着一些新建中小机场的陆续投运,这种状况日益明显。为了提高机场自身的竞争力,机场会对内部的航空公司进行激励,或者有的机场直接与其进行合作,这样进一步加剧了机场间的竞争,使得多机场区域内机场发展不均衡问题更加严重。
中小机场的发展直接影响了多机场区域的发展质量。因此,增加中小机场的市场份额,提高其收益,从而提高其竞争力,是改善多机场区域机场间发展不均衡的有效途径。国内关于改善多机场区域中小机场运营状况的研究,学者们大多从机场自身因素角度给出建议,但是机场与航空公司作为航空服务的提供者有着紧密的联系,而从机场与航司两者的内部联系进行的研究少之又少。从机场与航空公司的关系着手,研究机场与航空公司进行合作时对多机场区域机场竞争的影响,旨在对中小机场发展给出新的对策,从而改善多机场区域机场发展不均衡状况。
1 文献评述
1.1 低成本航空公司的相关研究
国外学者针对低成本航空的研究较早,在20世纪80年代初就有国外学者开始针对美国西南航空公司展开相关研究,发现美西南航空成功的秘诀在于其拥有深厚的历史底蕴和经营经验,其单一机型、单一服务、高飞机利用率和二线机场策略等低成本措施是其成功的关键,以及对于员工的重视也是其成功不可或缺的部分[4-5]。
之后随着低成本模式从美国走向欧洲,再从欧洲走向亚洲,低成本航空开始在全球遍地开花,越来越多的学者将自己的研究领域投向了这里。国内针对低成本航空公司的研究相对较少,也开始得较晚,基本都始于2000年以后,特别是春秋航空成立以后才有大量的研究文献出现,并多以春秋航空为案例进行研究[6-12]。国内外学者关于低成本航空公司的研究主要是对低成本航空公司的定义、发展趋势、运营成本、航线网络、竞争力等方面进行深入的研究。研究发现,航空运输自由化的发展是低成本航空公司崛起的最主要原因[13],低成本航空公司主要在工资的成本、燃油的成本以及航材的成本3个方面占有优势[14],Klophaus等提出目前欧洲多数传统航空公司加入了争夺短程航线的战役中,使得低成本航空公司不得不改变或增强自身的经营策略。但这些研究大多仅从低成本航空公司自身的因素进行,涉及低成本航空公司与机场的关系的研究很少。
1.2 机场与航空公司进行合作的相关研究
机场在经历了几十年的垄断后,竞争日趋激烈。航空管制的放松,低成本航空公司(LCC)的出现,以及机场的商业化和私有化是改革机场行业竞争动态的主要因素[14-16]。为了提高自身的竞争力,机场会与内部的航空公司进行航线补贴,收入分享等,以提高航空公司的运营积极性,从而达到提高吞吐量的目的。有的机场还会与内部的航空公司进行合作,因为合作对于双方的发展都存在益处,对于航空公司而言,通过确保关键机场设施获得竞争优势,而对于机场来说,则可以获得航空公司的财政支持以及稳定的业务量[17]。在市场不对称的情况下,航空公司存在纵向差异化时,机场往往与内部占着主导地位的航空公司签订协议进行合作提高自身的竞争力,如中小机场会与低成本航空公司串通合谋与核心机场争夺客源[18]。
还有部分学者对机场和航空公司之间的具体协议进行了研究。Starkie[19]和Fu等[20]研究了机场与航空公司之间的几种合作方式:①长期终端租赁。如墨尔本机场和维珍蓝航签订的为期10年的协议,让该航空公司从原安西特国内终端运营。②机场设施使用的长期协商费用。如沙勒罗伊机场向瑞安航空提供50%的着陆费用折扣。③机场签署国航空公司的地位。如达拉斯、奥兰多和亚特兰大机场。④特许权收入分成。如美国坦帕机场、欧洲瑞安航空[21]、慕尼黑机场经营公司和德国汉莎航空公司[22]等,机场通过收入分享变相补贴航空公司,以此鼓励航空公司提高客运吞吐量。并且机场更愿意与占主导地位的航空公司分享收益以获得最大利益[23]。⑤航空公司在机场的所有权。如汉莎航空在慕尼黑机场2号航站楼拥有40%的股份。
综上,低成本航空公司的出现加剧了机场竞争,而机场与航空公司作为航空服务的供给方,有着紧密的联系。而在多机场区域内,低成本航空公司对机场间的竞争有着怎样的影响呢?低成本航空公司与次要机场进行合作能否改善提高中小机场的吞吐量从而改善多机场区域机场发展不均衡的状况呢?这正是本研究要回答的问题。
2 基本模型
多机场区域中的机场群由核心的大机场和中小机场组成。在多机场区域中不同类型的机场都有自己的市场定位,核心机场侧重于服务FSC(全服务航空公司),为旅客提供高品质的服务,中小机场为节约成本,侧重于服务LCC(低成本航空公司)。因此,假设区域内的主要机场内只存在全服务航空公司,次要机场内只存在低成本航空公司,观察机场与内部航司进行合作时对多机场区域机场竞争的影响。
2.1 参数假设
假设区域内有两家机场B和D,机场B为次要机场,机场D为主要机场;次要机场B内有份额占比为1的航空公司a1(a1为低成本航空公司),主要机场D内有份额占比为1的航空公司a2(a2为全服务航空公司);假定两个机场的单位服务成本分别为cB、cD,cB远小于cD;向机场收取的单位费用分别为pB、pD,两个机场单位旅客的特许经营收入均为k,为了简化模型令k=0;航空公司a1、a2的航空票价分别为p1、p2,单位成本分别c1、c2,c1远小于c2;机场B、D对航司a1、a2的航线补贴分别为s1、s2;假设机场位于一条1 km长的线的两端,B在左端,D在右端。乘客根据他们的位置(或居住地)沿这条线均匀分布。一个位于x的消费者有一个单一的运输成本t,并且在去B机场和乘坐a1航空公司的航班以及去D机场和乘坐a2航空公司的航班之间无差异,可以用Hotelling条件表示为
p1+tx=p2+t(1-x)
(1)
解得
(2)
(3)
2.2 收益分析
和单个机场的模型相似,在这里也采用逆向归纳法。首先确定下游市场(航空公司)的利润最大化问题,然后再确定上游市场(机场)的利润最大化问题。
2.2.1 机场B与航司a1,机场D与航司a2均不合作时的收益
机场B与航司a1的收益分别为
π1=(p1-c1-pB+s1)xB
(4)
πB=(pB-s1-cB)xB
(5)
机场D与航司a2的收益分别为
π2=(p2-c2-pD+s2)xD
(6)
πD=(pD-s2-cD)xD
(7)
首先求解航空公司a1、a2的最佳反应函数,即a1、a2的收益函数对p1、p2的一阶最优条件将解得的p1(pB、pD)、p2(pB、pD)代入机场B、D的收益函数,得到πB(pB、pD)、πD(pB、pD),再求解B、D的收益函数对pB、pD的一阶最优条件,解得
(8)
(9)
(10)
(11)
(12)
(13)
因此,机场B与航司a1,机场D与航司a2均不合作时,机场B与航司a1的收益分别为
(14)
(15)
机场D与航司a2的收益分别为
(16)
(17)
2.2.2 机场B与航司a1合作,而机场D与航司a2不合作时的收益
机场B与航司a1的联合收益为
πa1B=(p1-c1-cB)xB
(18)
机场D与航司a2的收益分别为
π2=(p2-c2-pD+s2)xD
(19)
πD=(pD-s2-cD)xD
(20)
首先机场B与航司a1的联合收益函数、航司a2的收益函数分别对p1、p2的一阶最优条件,将解得的p1(pB、pD)、p2(pB、pD)代入机场D的收益函数得到πD(pB、pD),求解机场D的收益函数对pD的一阶最优条件,解得
(21)
(22)
(23)
(24)
(25)
因此,机场B与航司a1合作,机场D与航司a2不合作时,机场B与航司a1的联合收益为
(26)
机场D与航司a2的收益分别为
(27)
(28)
2.2.3 机场B与航司a1不合作,机场D与航司a2合作时的收益
机场B与航司a1的收益函数分别为
π1=(p1-c1-pB+s1)xB
(29)
πB=(pB-s1-cB)xB
(30)
机场D与航司a2的联合收益为
πa2D=(p2-c2-cD)xD
(31)
求解机场D与航司a2的联合收益函数与航司a1的收益函数分别对p2、p1的一阶最优条件,将解得的p1(pB、pD)、p2(pB、pD)代入机场D的收益函数得到πB(pB、pD),再求解机场B的收益函数对pB的一阶最优条件,解得
(32)
(33)
(34)
(35)
(36)
因此,机场D与航司a2合作,机场B与航司a1不合作时,机场D与航司a2的联合收益为
(37)
机场B与航司a1的收益分别为
(38)
(39)
2.2.4 机场B与航司a1合作,而机场D与航司a2也合作时的收益
机场B与航司a1的联合收益为
πa1B=(p1-c1-cB)xB
(40)
机场D与航司a2的联合收益为
πa2D=(p2-c2-cD)xD
(41)
求解机场B与航司a1、机场D与航司a2的联合收益函数分别对p1、p2的一阶最优条件为
(42)
(43)
解得
(44)
(45)
(46)
(47)
因此,机场B与航司a1、机场D与航司a2的联合收益分别为
(48)
(49)
2.3 博弈均衡分析
机场与航司的收益支付矩阵见表1。
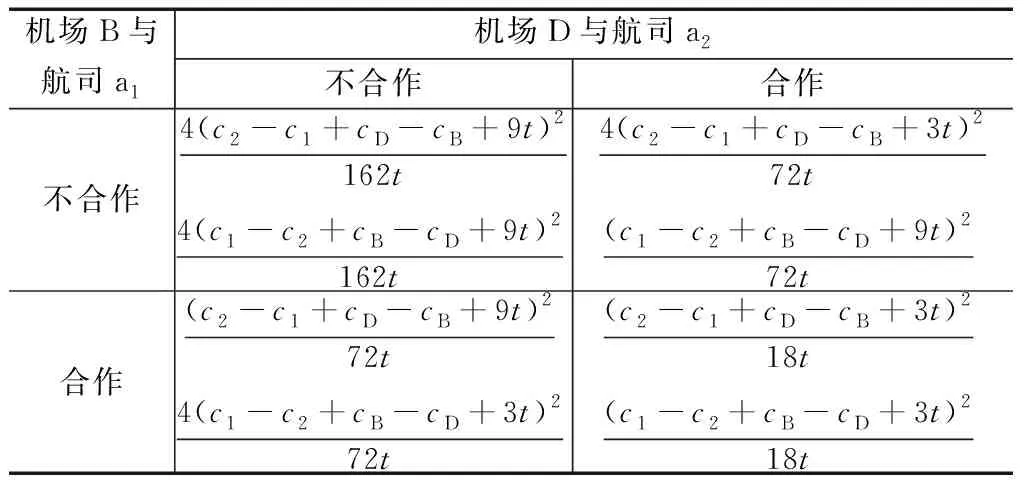
表1 机场与航司的收益支付矩阵

3 机场与航司的利益分享模型
“讨价还价模型”是鲁宾斯坦(Rubinstein)提出的合作博弈的利益分享模型。在该模型里,参与人1首先出价,参与人2可以选择的策略为接受或拒绝。如果参与人2接受,那么博弈结束,利润分配原则根据参与人1的方案;如果参与人2拒绝,那么参与人2将进行还价,此时参与人1的策略为可以接受或拒绝;如果参与人1接受,那么博弈结束,利润分配原则按参与人2的方案分配;如果参与人1拒绝,那么他再出价;如此循环,直到一个参与人的出价被另一个参与人接受为止。因此,这属于一个无限期完美信息博弈,参与人1在时期1,3,5,…出价,参与人2在时期2,4,6,…出价。
3.1 模型假设
假设1:假定行动先行者为机场。博弈的两个参与者是航空公司和机场,机场的利润分配份额为y,航空公司的利润分配份额为1-y。
假设2:设机场B与航司a1进行合作比两者不进行合作时的总利润多出的剩余利润为z,机场和航空公司分享的是剩余利润W=πa1B-(πB+π1)总利润。

假设4:航空公司的贴现因子为δ1,机场的贴现因子为δB,贴现因子可以表示参与人的耐心程度,其取值在0到1之间,贴现因子越大说明参与人的耐心越好,如果等于0则说明参与人完全没有耐心。因此可以把贴现因子理解成为参与人的耐性,并且0<δB<1,0<δ1<1。
3.2 模型分析
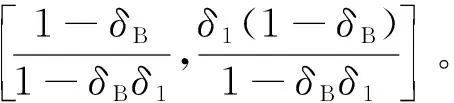
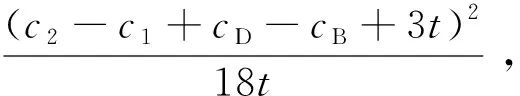
当机场B与航司a1的合作稳定时,机场获得的剩余利润为
(50)
同理航空公司获得的剩余利润为
(51)
根据WB分别对δB和δ1求一阶偏导得
(52)
(53)
从一阶导数可以看出,机场与航空公司所分配的利润随自身的贴现因子的增大而增大,随对手的贴现因子的增大而减少。因为贴现因子表示参与者分配剩余利润的耐心程度,所以这就变成了一场耐心的较量,局中人谁越有耐心,谁获得的份额就越高。
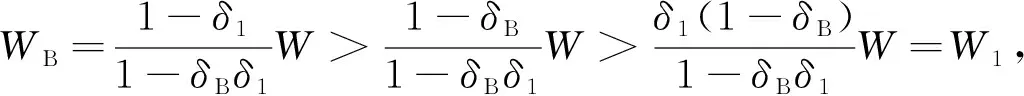
通过以上的分析可以看出,较高的机场与航空公司的贴现系数可以维持战略合作的稳定,只要参与双方足够有耐心,最后就能达到平分剩余利润的状态。但是,完整的航空服务要通过机场与航司共同的协作才能够完成,所以双方都应该长远地看待并且积极维护其战略联盟关系。
结论2:机场与内部航空公司合作形成的战略联盟带来剩余利润,两者在分享这一剩余利润时最有利的对策是提高自身的耐心程度,这样不仅可以维持长期的战略联盟关系,最终还可以平分剩余利润。
4 结论