重型半挂汽车避撞控制的研究
2022-05-05汪选要
王 鑫,汪选要
(安徽理工大学机械工程学院,安徽 淮南 232001)
0 引言
根据中国国家统计局的数据,截至2021年6月,全国共发生约23.8万起交通事故,约6.7万人死亡,造成了巨大的生命财产损失[1]。未保持合理的安全距离、路面情况和驾驶员主观行为等因素是造成交通事故的重要成因。其中,驾驶员因素被认为是事故的主要原因。同时,车间安全距离也是交通安全最重要的指标之一[2]。
为了提高避撞系统的安全性与准确性,国内外众多学者开展了相关研究。Li等[3]采用集成ACC(自适应巡航控制)、RSC(后轮转向控制)和RBC(侧倾制动控制)的主动安全协同系统,以智能汽车在紧急情况下主动避撞控制问题。Chen等[4]提出了一种计算前后两车之间安全制动距离的新算法,但未考虑了周围环境的影响;Wang等[5]使用单因素方差分析方法对比分析了实际跟车工况下影响期望安全距离的主要影响因素;Jansson 等[6]提出以ACC实现汽车主动避撞,并建立了行车风险场模型;章军辉等[7]针对碰撞预警系统存在的漏警虚警问题,以跟车车距、自车与前车相关信息和路面附着系数为输入,提出了基于BP神经网络的自学习纵向避撞安全辅助算法;袁伟等[8]为了解决现有汽车避撞控制策略及碰撞风险指标单一的问题,基于避撞距离模型划分安全行驶区域,提出了制动和转向协同的主动避撞控制系统。
安全距离是驾驶员判断车间距离是否安全的重要依据,上述文献对系统安全距离的设计具有一定的局限性,造成了避撞系统使用率降低。针对上述问题,本文围绕重型半挂汽车主动避撞系统中的安全距离,提出了一种综合考虑驾驶员主观行为和环境因素的安全距离模型,制定了避撞系统分层控制策略,通过Trucksim和Simulink软件联合对典型避撞工况进行仿真分析,验证所提出控制策略的避撞控制效果。
1 车辆逆动力学模型搭建
1.1 节气门控制模块
根据文献[9]忽略空气密度的变化,车辆在水平路面加速行驶时,可得到车辆行驶方程为
(1)
式中:m为汽车总质量,kg;ad为期望加速度,m/s2;Ft为车辆的驱动力,N;Fb为制动器制动力,N;Cd为空气阻力系数;A为车辆迎风面积,m2;ρ为空气密度,kg/m3;v为自车车速,km/h;g为重力加速度,m/s2;f为滚阻系数。
忽略传动部件连接处的弹性变形。根据当前档位速比,可得发动机输出转矩Td为
(2)
式中:Kd为制动力与制动主缸压力比值。
根据式(2)结合发动机特性图,在Simulink软件中通过二维查表获得期望节气门开度αd为
αd=f(Td,ωe)
(3)
式中:ωe为发动机转速,r/min。
1.2 制动器控制模块
在制动时发动机力矩输出为0,即Ft=0,将式(1)改写为
(4)
期望制动主缸压力Pd为
(5)
式中:Kb为制动力与制动压力的线性系数。
1.3 驱动与制动模式切换策略
在车辆正常行驶过程当中,是不允许驾驶员既操纵制动踏板又踩踏加速踏板的情况,避免对车辆造成损伤。本文依据上述原则制定了切换逻辑,为提高在操作过程中车辆的平稳性,设置了缓冲区域Δh,本文取Δh=0.1,根据期望加速度αd和实际加速度αf定义切换逻辑:
1)当ad-af>Δh时,加速踏板控制。
2)当-Δh 3)当ad-af<-Δh时,制动踏板控制。 实现整车避撞功能的基础是确定准确可信的行车安全距离,固定安全距离模型(CTH)和可变安全距离模型(VTH)是当前主流的安全距离模型划分出的2大类[10],其他行车安全距离模型可认为在此基础上的优化与发散。 不同的路面附着系数会影响汽车的制动过程,同时,驾驶员因素也会影响行车安全距离,本文参考文献[11]改进并提出了一种综合路面附着系数和驾驶风格的安全距离模型。当前车静止时,自车匀速行驶接近前车,车距不断减小,此时安全距离S1模型为 (6) 式中:t1为制动持续时间;e为驾驶风格选择系数。 当前车匀速行驶时,自车车速仍大于前车车速,为避免两车发生碰撞,此时安全距离模型S2为 (7) 式中:μ为路面附着系数;a为制动减速度,m/s2;v1为前车车速,km/h。其中,最小安全保持间距d0可表示为 (8) 式中:c为驾驶员意图参数;b为模型参数。 驾驶风格选择系数i定义如下: (9) 对于驾驶员反应时间t,现有安全距离基本采用固定值计算,通常取0.2~1.2 s,根据文献[12-13]表明驾驶员反应时间t与驾驶员驾龄、心理状况等因素有关,针对上述问题,本文采用模糊控制理论来确定,以驾驶员综合指标值和车速作为模糊控制器输入,驾驶员反应时间作为输出,表1为不同驾龄对应的综合指标值Q。 表1 不同驾龄对应的综合指标值 根据表1数值将论域设置为[40,100],车速论域设置为[40,80],驾驶员反应时间论域设置为[0.2,1.2],表2为本文制定的模糊规则表,隶属度函数三维关系如图1所示。 表2 模糊规则表 图1 模糊控制隶属度函数三维关系 Trucksim软件广泛应用于商用车动力学仿真领域,其外部有众多拓展接口可供连接,本文选择调用Matlab/Simulink实现二者的联合仿真,仿真参数如表3所列。 表3 仿真参数 为验证所提出安全距离模型的准确性,现分别采用CTH模型、VTH模型与提出的改进安全距离模型(Proposed model)进行仿真对比。3种安全距离模型仿真结果如图2所示。 图2 3种安全距离模型仿真曲线 由图2可知,自车匀速、前车静止状态下,各模型表现均比较稳定,其中,VTH模型相对比较保守,所预留的安全距离较大,道路利用率较低,本文所设计的安全距离模型对比CTH模型较为一致,总体而言,在前车静止状态下,上述模型的仿真结果相差不大,较为符合逻辑。 滑模控制是变结构控制系统的一种非线性控制方法,因其结构简单、响应快和鲁棒性高等优点被而广泛应用。上层控制器主要根据相对距离、相对速度和实际加速度,确定当前所需的加速度。本文选取相对距离误差和相对速度误差作为评价控制系统的指标,并以此进行滑模跟踪控制。 定义跟踪误差为 e(t)=Dr-Ds (10) e(t)′=v1-v (11) 式(10)(11)中:e(t)为跟踪误差;Dr为两车相对距离,m;Ds为两车安全距离,m;e(t)′为e(t)的微分。 设计滑模面S为 S=e(t)′+pe(t) (12) 式中:p为滑模面系数,p>0。为减小系统抖振,设计滑模趋近率为 S′=-jsgn(S)-kS(j>0,k>0) (13) 式中:S′为S的微分;k为指数趋近率;常数j表示移动点向滑动面移动的速率。如果常数j很小,则接近速度很慢;如果常数j较大,系统因不稳定而出现抖动。结合式(12)和(13)可求得控制量 a1=a2+pe′(t)+kS+jsgn(S) (14) 传统PID控制器参数需要根据专家经验多次试凑以获得最优控制参数,试凑过程烦琐、不确定性高、效率低。而粒子群算法(PSO)作为一种群体优化智能算法,通过设计无质量的粒子模拟鸟群个体,以获得目标最优解,本文选择以上层控制器求解出的期望减速度与实际减速度的差值作为PID控制器的输入,采用ITAE准则作为评价适应度值的标准,通过PSO算法整定Kp、Ki、Kd参数,以获得最优PID控制。设置最大迭代次数为100,种群规模为30,适应因子为2,粒子速度上下限分别为1和-1,其中Kp范围为[0,10],Ki范围为[0,120],Kd范围为[0,10]。经PSO迭代寻优后的Kp、Ki、Kd值分为5.47、100、0,此时适应度值为122.39,仿真结果如图3所示。 根据前文搭建的安全距离模型和控制器,验证上述避撞系统的有效性,选用前车静止和前车匀速的仿真工况,采用Trucksim和Matlab/Simulink进行联合仿真。 设定自车以50 km/h的速度匀速驶向静止的前车,仿真时间设定为10 s,两车初始距离为60 m,当自车(Host car)与前车(Front car)距离较大时,自车保持匀速行驶,避撞系统控制器采取措施,当两车间距离小于安全距离,有碰撞风险时,后车开始制动,仿真结果如图4~5所示。 由图5可知,仿真初始阶段,自车与前车的间距较大,两车无碰撞风险,自车匀速行驶,在1.5 s时,两车相对距离约为40 m,两车相对距离小于安全距离,自车紧急制动;自车车速由50 km/h迅速减小,在5.1 s时,自车停止运动,车速为0,期望最小安全保持间距为6 m,此时激进型驾驶员将两车间距保持在6.5 m附近,对于成熟型驾驶员会将两车间距保持在8.1 m附近,而保守型驾驶员会增大两车间距达到9.75 m,符合现实情况,同时也验证了避撞控制系统能够在前车静止的工况下实现避撞功能,证明了所提出的安全距离模型的准确性。 在前车匀速行驶的工况下,设置前车车速为18 km/h,前车减速度为0,自车初始车速为60 km/h,两车初始距离为60 m,仿真时间设定为10 s,仿真结果如图6~7所示,仿真时自车和前车同时起步,前2.5 s时刻内,两车车距较大,满足安全距离的条件,两车相距约为30 m,在2.8 s时两车车距低于安全距离,制动器工作,自车开始减速,在8.1 s时,自车车速减小到18 km/h并与前车一同匀速行驶,此时激进型驾驶员会将安全车距保持在9.6 m左右,保守型驾驶员安全车距达14.4 m,驾驶风格越激进,安全车距值越小,符合实际驾驶习惯,可以证明在前车匀速行驶的工况下,避撞控制系统能够及时触发,以达到避撞效果。 a.Kp参数迭代寻优曲线 b.Ki参数迭代寻优曲线 c.Kd参数迭代寻优曲线 d.粒子群算法适应度值变化曲线 图4 前车静止时两车车速仿真曲线 图5 前车静止时两车相对距离仿真曲线 仿真结果表明,本文所提出的安全距离模型和速度、距离跟踪误差滑模控制器能够实现重型半挂汽车避撞功能,验证了避撞控制系统的合理性和正确性。 本文提出了一种考虑驾驶员和环境因素安全距离模型,建立了重型半挂汽车纵向避撞控制系统,通过驾驶员参数确定模型参数的取值,采用上层滑模控制和下层PSO-PID控制的分层控制策略,设置了前车静止和前车匀速的仿真工况,通过Trucksim与Matlab/Simulink软件联合对控制系统进行了验证。结果表明,避撞控制系统能够在预知前车危险的情况下,实现自车紧急避撞,验证了不同驾驶风格下驾驶员对安全距离的把控,并且能够保证在安全距离下实现安全停车或跟车行驶,避免与前车相撞,提高了行车安全性。 图6 前车匀速时两车车速仿真曲线 图7 前车匀速时两车相对距离仿真曲线2 安全距离模型建立

2.1 驾驶员反应时间确定

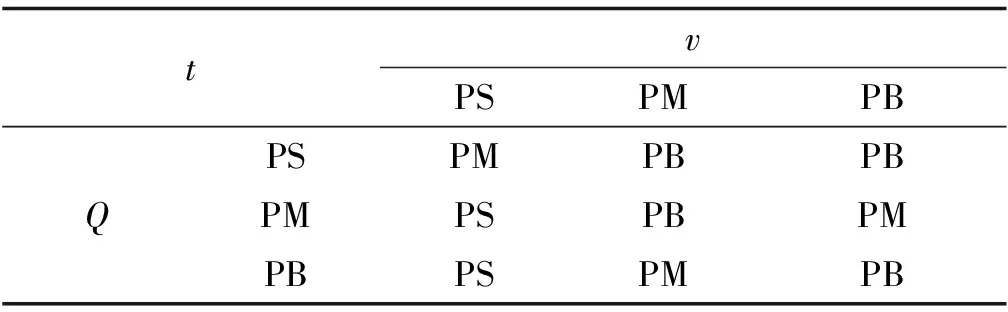
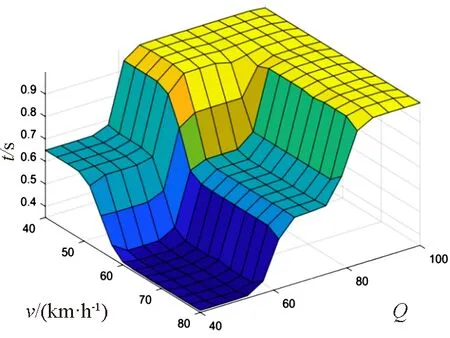
2.2 安全距离模型仿真
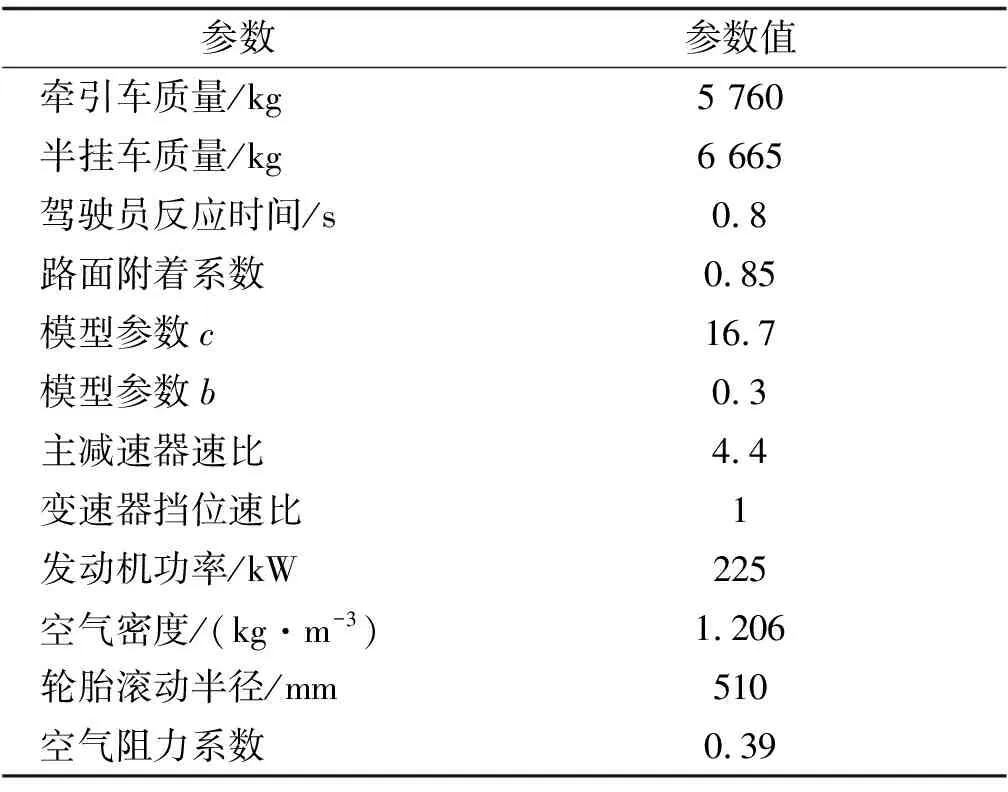
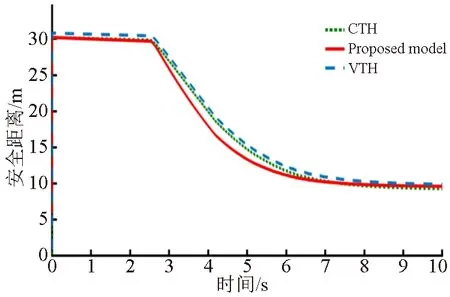
3 分层避撞控制器设计
3.1 上层控制器

3.2 下层控制器
4 仿真与分析
4.1 前车静止仿真工况
4.2 前车匀速行驶仿真工况
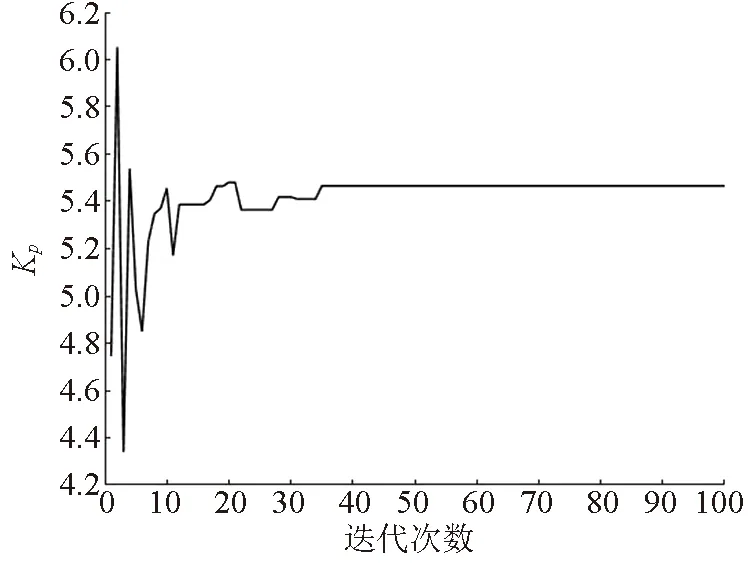

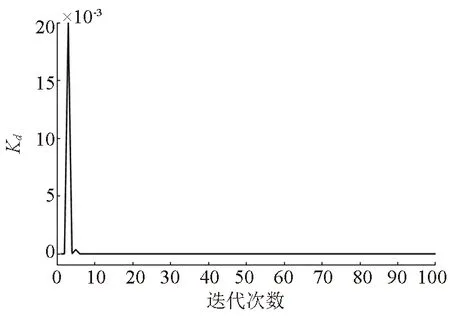


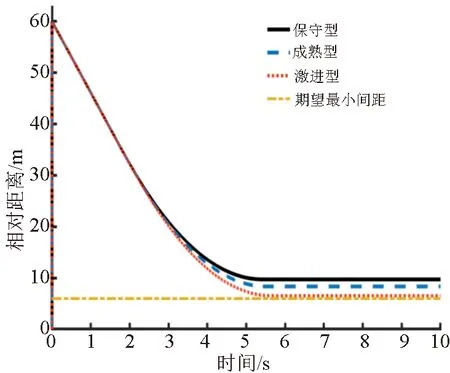
5 结语